[ 306 ]

u terstond voor zo'n grote gift (wat ik nu doe) dank te betuigen. En ik twijfel er niet aan of ik zal, zodra me de tijd gegeven zal worden dit door te nemen (wat pas zal gebeuren wanneer ik van hier naar huis terug zal keren), veel vinden wat U als schrijver waardig is, rijk aan eruditie, en voor mij zeer welkom. Intussen, terwijl ik dit schrijf, heb ik bij toeval onder ogen pagina 72 2) van uw boek, die ik bij het zien van mijn naam haastig lees. Waarop u mij weliswaar niet direct lijkt te beschuldigen van kwade trouw; u lijkt echter enige twijfel te hebben, of onze Neile 3) dat volkomen bereikt heeft, waarvan u zelf niet ontkent dat hij er zeker niet ver vanaf is geweest.

Maar nu ik dit zo haastig schrijf heb ik niet bij de hand wat ik over deze zaak heb geschreven. Ik ben er echter heel zeker van, dat ik daar geheel te goeder trouw gehandeld heb. En er was geen reden waarom ik meer partij zou kiezen voor Neile dan voor de waarheid; ik was hem niets verplicht door enige gunst, niet door innige vriendschap met hem verbonden, en ik herinner me niet hem ooit te hebben gezien toen ik dat schreef, of zijn naam anders dan bij die gelegenheid te hebben gehoord; en enige tijd later toen mijn werk was uitgegeven heb ik hem voor het eerst van dichtbij gezien, toen hij (op dat ogenblik als een volslagen onbekende) naar mij toekwam (er was toevallig een aanleiding)   2)  Op p. 71 en 72 van Hor. Osc., Pars tertia, na propositie IX, over de rectificatie van de semikubische parabool, leest men: "Rursus autem ... utique." [Ned.:]

En weer zijn we hier terechtgekomen bij een lijn waarvan anderen de lengte al eerder hebben afgemeten. Namelijk die waarvan Joh. [Hendrik] van Heuraet van Haarlem in 1659 heeft aangetoond dat ze gelijk is aan een rechte, en zijn bewijs is toegevoegd aan de commentaren van Joh. [Frans] van Schooten op de Geometria van Descartes, in hetzelfde jaar uitgegeven. En hij heeft wel als eerste van allen een kromme lijn, van de soort waarvan willekeurige punten meetkundig worden bepaald, tot deze afmeting herleid, toen Wren omstreeks dezelfde tijd de lengte van de cycloïde had gegeven, met een niet minder ingenieuze aanpak.   Ik weet inderdaad dat, nadat de vondst van van Heuraet was uitgegeven, de zeergeleerde Wallis die heeft willen toekennen aan William Neile, een jonge edelman en landgenoot, in het boek over de Cissoïde. Maar mij lijkt, als ik nauwkeurig afweeg wat hij daar aanvoert, dat Neile zeker niet ver van die vondst af is geweest, maar toch deze niet geheel heeft bereikt. Want het blijkt ook niet uit zijn bewijs, dat Wallis aanvoert, dat hij voldoende doorzien heeft wat voor kromme dat zou zijn, waarvan hij zag dat de afmeting gegeven zou worden als ze geconstrueerd werd. En als hij had geweten dat het een van de krommen was die al lang bij de meetkundigen bekend waren, is te geloven dat of hij zelf, of anderen uit zijn naam, tijdiger mededeling hadden gedaan aan de meetkundigen van een zo edele vondst, die meer dan iets anders verdiende dat ze het Archimedische heureka zouden uitroepen. Het is zeker dat van deze vondst, als een eigen bijdrage, ook Fermat, senator in Toulouse en ook zeer bedreven in de meetkunde, bewijzen heeft opgeschreven, die in 1660 gedrukt zijn, maar die zijn in elk geval te laat.

Als Aanhangsel No. 1948 laten we volgen het bewijs van William Neile, door Wallis gepubliceerd op p. 92 van zijn boek, aangehaald in brief No. 690, noot 3 [Tractatus duo ... De Cissoide (1659);  fig. 23].   Men zal opmerken dat Neile de ordinaat van de kromme, waarvan hij wil bewijzen dat hij te rectificeren is, definieert met de voorwaarde dat ze evenredig is met het oppervlak van een paraboolsegment waarvan de hoogte gelijk is aan de abscis van de kromme. Daar het oppervlak van zo'n segment welbekend was, zou het niet moeilijk zijn geweest er de vergelijking van de kromme uit af te leiden, en er een parabolische kromme in te herkennen. Huygens veronderstelt dat Neile deze stap niet heeft gemaakt, omdat hij er anders wel melding van zou hebben gemaakt, gezien het belang dat zijn ontdekking erdoor verkreeg.   Dezelfde opmerking is van toepassing op het bewijs van Brouncker, gepubliceerd door Wallis als vervolg op dat van Neile. Pas bij zijn eigen bewijs, dat daarna komt, duidt Wallis de kromme aan als semikubische paraboloïde [nu: semikubische parabool, een paraboloïde is nu een omwentelings­lichaam].   3)  William Neile, zie brief No. 1746, noot 3.

[ 307 ]

en me ervoor bedankte dat ik hem daar had vermeld. Doch wat u toevoegt, Dat het te geloven is, als hij voldoende had geweten van de zaak, dat of hij zelf, of anderen uit zijn naam, tijdiger mededeling hadden gedaan aan de meetkundigen van een zo edele vondst: heel tijdig (zeg ik) is die zaak aan de meetkundigen meegedeeld, en om zo te zeggen in één klap is ze algemeen bekend geworden, en door hen met de grootste lof ontvangen, en althans door onze meetkundigen gekend en erkend, en algemeen verbreid door dat gezelschap van mannen, waaraan later de naam Royal Society is gegeven.

En dit in die mate, dat in de tijd van een maand, na Neile, in elk geval Wren, Rooke, en Brouncker (in die volgorde, als ik me niet vergis) afzonderlijk dezelfde zaak bewezen hebben; maar allen hebben aan Neile de eerste eer gelaten. En zeker heeft de zeer illustere Brouncker zijn bewijs terstond naar mij in Oxford gestuurd, juist datzelfde, dat ik daarna (in het Latijn vertaald) heb uitgegeven, zonder dat er een woordje (voorzover ik weet) veranderd is. En hij voegde er aan toe, dat hetzelfde eerder al door verscheidenen was bewezen, maar het eerst door Neile. Ik heb het mijne erachter bijgevoegd, ik geloof als laatste van allen, en ik heb tegelijk voor deze kromme een naam ingevoerd, Semikubische Paraboloïde noemde ik hem; dat de aard van de kromme door de onzen voldoende is doorzien, is niet iets dat u terecht kunt betwijfelen.

En het zou wel een wonder zijn als niemand van de onzen, met zoveel als we waren, in staat zou zijn geweest van een lijn, die met zoveel methoden was aangetoond, de ware aard te achterhalen; en dat nu Huygens ons dit zou verwijten had ik niet verwacht. Niemand van de onzen heeft de zaak met anderen in het buitenland gedeeld (en de onzen waren, althans in die tijd, er niet zeer op gericht, tenzij ze werden uitgedaagd, de roem van hun vondsten uit te breiden; zeker Neile zou dit nooit gaan doen), maar die zaak, al wijd en zijd erkend, en ook door verscheidenen bewezen, werd bij ons niet gehouden voor iets nieuws, al lang voordat Heuraet op die bespiegeling kwam 4), wat een heel jaar later is gebeurd. En zelfs als Heuraet in het jaar 1659 dit heeft gevonden, zoals u zegt, dat wat u verder beweert, namelijk dat hij als eerste van allen een kromme lijn, van de soort waarvan willekeurige punten meetkundig worden bepaald, tot de afmeting met een rechte lijn herleid heeft, is, verklaar ik onverschrokken (en er zijn voor mij ook betrouwbare getuigen die nog in leven zijn) volstrekt anders. Immers, van de onzen hebben velen, zoals u ziet, diezelfde kromme al het jaar daarvoor zo herleid.

Maar er moet ook niet gedacht worden (wat echter voor de zaak niets uitmaakt) dat wij, althans allen, niet hebben geweten hoe die kromme lijn was die we zo hadden geconstrueerd; ofschoon als allen of iemand ook dit niet heeft geweten (wat ik echter niet toegeef) vaststaat dat tenminste deze bewerking ervan voldoende doorzien is; namelijk dat de zo geconstrueerde kromme gelijk is aan een bekende rechte; wat het voorgestelde was. Maar ook, dat het een kromme van dien aard is dat willekeurige punten ervan meetkundig kunnen worden bepaald; het was gemakkelijk aan te tonen uit het bewezene, als iemand er onderzoek naar zou doen. Voor mij tenminste was dit voldoende zeker, en ook voor de anderen, geloof ik.   4)  Men kan de datum nauwkeuriger geven. In de brief aan van Schooten van 13 januari 1659, gedrukt in Geometria, Pars I, p. 517 van de uitgave van 1659, en die voorafgaat aan de 'Epistola de transmutatione curvarum linearum in rectas', zegt van Heuraet dat hij hetgene dat hij aan van Schooten stuurt heeft gevonden "toen ik dacht over een reis naar Frankrijk". En volgens brief No. 587 [in PS] vond het vertrek naar Frankrijk plaats 8 maanden voor 13 februari 1659.

[ 308 ]

Ja inderdaad, aangezien Neile deze hele bespiegeling uit het scholium van prop. 5) van mijn Arithmetica Infinitorum [1656] had afgeleid, dat deze kromme een soort Parabolische kromme is, lag het zo voor de hand voor iedereen, dat het niet noemenswaard was: ook ik meende niet dat ik iets nieuws had gezegd, toen ik Paraboloïde had gezegd; maar wel dat hij handig semikubisch genoemd kon worden, een naam die niet eerder was gekozen. Doch omdat dit niet is uitgegeven (om die reden die ik hiervoor al aangaf) beken ik openhartig hoe het zit (geef vergiffenis aan wie bekend heeft*)), namelijk dat het door mijn schuld gekomen is.

Immers, in de tijd dat de zeer geëerde heer Brouncker zijn bewijs aan mij stuurde (in het jaar 1658°) in de maand, als ik me goed herinner zonder mijn papieren bij de hand te hebben, juni of juli) verzocht hij me tegelijk dit in een geschrift van mij te zetten 6) dat toen onder de pers was (ik ben nu van gevoelen dat ik dit gewoon had moeten doen; en hoewel hij me het nalaten hiervan niet als schuld heeft aangerekend, reken ik het mezelf wel aan). Maar deels door mijn onverschilligheid, deels doordat Neile mij toen geheel onbekend was, en ik het bewijs niet gezien had van degene die het als eerste had opgesteld, maar alleen dat van de zeer geëerde Brouncker; deels omdat ik toen niet zag dat er haast bij was, maar meende dat het òf door iemand anders kon worden uitgegeven als het nodig leek, of een andere keer door mij; kwam het er inderdaad op neer, dat noch ik het toen heb uitgegeven, noch iemand anders er zorg voor droeg, en wel het minst van allen degene voor wie het juist van belang was.

Maar daarom moet Neile, die nu niet meer in leven is, niet van zijn roem worden beroofd, net zo min als u van de uwe, zoals u van enkele daaropvolgende proposities zegt 7) dat u ze mij in geschrifte hebt meegedeeld, en mij als getuige oproept; hoe dan ook, u hebt ze niet gepubliceerd. Doch zolang u eraan twijfelt of het alleen om deze reden niet is gedaan, ingaand tegen het getuigenis van zoveel mensen en de bekendheid van degene die het steunt, daarom omdat we niet terstond luid hebben geroepen (en gedrukt) 'heurèka': nu, dan kent u de Engelsen slecht. Want wat er ook te menen is over Fransen of ook Nederlanders, zeker is dat Engelsen niet gewoon zijn zich altijd zo op iets te beroemen. En juist die zeer uitstekende vondst van Harvey over de bloedsomloop (om er niet meer te vermelden) was zo goed als twintig hele jaren bij de onzen bekend, erkend en openlijk goedgekeurd, voordat ze in druk werd geopenbaard.

Maar u, beste heer, gaat u door zoals u gewoon bent met het verrijken van de goede letteren en het begunstigen van de geleerden; het ga u goed.   5)  Lees: 38e prop. [Scholium op p. 28].   [ *)  Lat. "da fasso veniam", naar Ovidius, 'Ex ponto', IV, 23: "da veniam fasso".]   [ °)  Een jaar eerder, volgens Philip Beeley & Christoph J. Scriba (eds.), Correspondence of John Wallis (2014), vol IV, p. 195.  Zie brief No. 1955.]   6)  Commercium epistolicum [1658], aangehaald in brief No. 497, noot 3.   7)  Als vervolg op propositie IX van Pars tertia, p. 73 van Horologium oscillatorium leest men "Anno autem insequenti [1658] ... supersederem" [Ned.]:

En het jaar daarna heb ik ook oppervlakken van hyperbolische en sferoïdische conoïden gevonden, hoe ze tot cirkels herleid konden worden, en de constructies van problemen erover heb ik, evenwel zonder het bewijs toe te voegen, meegedeeld aan meetkundigen met wie ik toen een briefwisseling had, in Frankrijk aan Pascal en anderen, in Engeland aan Wallis, die niet lang daarna ook zijn subtiele vondsten hierover, samen met veel andere, in het licht gaf, en maakte dat ik er van afzag onze bewijzen te voltooien.

[ Zie J. Wallis, Tractatus duo (1659), p. 98, 103.  Dit GWLB-ex. heeft marginalia van Huygens op p. 95-99:   Op p. 95, naast het onderstreepte "Van deze kromme dan staat vast, dat hij behoort tot de soort Parabool-achtigen", staat geschreven: "Hoc Neilius et Bronckerus et ipse Wallisius nesciebant antequam Heuratius docuisset, nam si scivissent non neglexissent promere tam novum atque insigne inventum", oftewel: "Dit wisten Neile en Brouncker en Wallis zelf niet voordat Heuraet het bekend had gemaakt, want als ze het hadden geweten, hadden ze niet verzuimd een zo nieuwe en uitstekende vondst aan het licht te brengen".   Op p. 96, naast het onderstreepte "en zelfs als eersten" (nl. de onzen), staat geschreven: "fortasse, sed curvam quae esset non ostenderunt", oftewel: "misschien, maar welke kromme het was hebben ze niet laten zien".   Op p. 97, naast "zoals de ordinaatsgewijs gelegden bij de toegevoegde as van de Hyperbool", staat: "hoc etiam nesciebas antequam ostenderit Heuratius. Sed ego jam ante inveniram et Heuratio inveniendi ansam praebui", oftewel: "ook dit wist je niet voordat Heuraet het heeft aangetoond. Maar ik was er al daarvoor opgekomenen en ik heb Heuraet een handvat gegeven bij het vinden".   Op p. 98, naast "Wat ook u ergens hebt opgemerkt", staat: "imo omnium primus", oftewel: "ja zelfs als eerste van allen".   Op p. 99, naast "Bezie, als u wilt, of dit overeenkomt met uw vondsten", staat de kanttekening: "Hoc ipse videre poteras, nam jam pridem illa mea inventa ad te miseram", oftewel: "Dit had je zelf kunnen zien, want al eerder had ik je die vondsten van mij gestuurd"; zie hiervoor T. II, p. 330.]

[ 309 ]

No 1948. J. Wallis aan Christiaan Huygens. 1) 1659.   Aanhangsel II bij No. 1946. { Curva Paraboloidis Semicubicalis.   Fig. 23.}   Het bewijs van Neile, dat hij (zoals gezegd is) twee jaar geleden bekend gemaakt heeft, was als volgt. 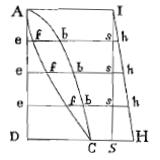  AbCD zij een rechte parabool; waarvan de as AD verdeeld wordt in gelijke heel kleine delen ee; en bij de punten e worden ordinaatsgewijs gelegd de rechten ef, evenredig met Aeb van de parabool. En laat de rechthoek DSI, zijn tot de parabool ADC, als AD tot DC. Vervolgens zij eh in het kwadraat overal gelijk aan de kwadraten van es, eb samen.   Ik zeg ten eerste, dat onderling gelijk zijn de verhouding van de figuur ADHI, de rechthoek DI, & de parabool ADC, en die van de volgende lijnen: de kromme AfC en de rechten AD, DC.   2o.  Dat de rechten eh ordinaatsgewijs zijn gelegd bij de Parabool.   De rechten ef zijn immers, door constructie, evenredig met Aeb van de parabool; & daarom worden de verschillen van de rechten gemakkelijk voorgesteld met de rechthoeken eeb. De rechthoeken ees zijjn gelijk (en de som van alle is tot de som van alle eeb, als AD tot DC); dus ze stellen de rechten ee voor. De rechten ff zijn in het kwadraat gelijk aan de kwadraten van de rechten ee en van de verschillen van de rechten ef. En de rechthoeken eeh zijn overal in dezelfde verhouding tot de voorstellingen van die grootheden. Het eerste deel van de propositie staat dus vast.   De kwadraten van de rechten eb zijn rekenkundig evenredig. De kwadraten van de rechten ee zijn gelijk. Dus ook de kwadraten van eh zijn rekenkundig evenredig; en die rechten EH zijn de zijden van rekenkundig evenredige vierkanten; zodat ze zijn als een reeks van ordinaatsgewijs gelegden bij de parabool.   En dientengevolge: Er zal een rechte lijn geleverd kunnen worden die gelijk is aan de kromme AFC.   Zodra de illustere Brouncker dit bewijs van Neile had bekeken, stelde hij dadelijk het zijne op, niet ongelijk, dat volgt, en hij deed het mij toekomen; dat heb ik nu al meer dan twee jaar. En het is bijna zover gekomen dat ik het had ingelast in Commercium Epistolicum, door mij zo niet eerder uitgegeven, (aangezien ik het voor het eerst ontving in de tijd dat die brieven tussen ons en de heren Fermat en Frenicle werden gewisseld). Maar daar ik het bewijs van Neile (die het als eerste heeft gevonden) nog niet had gezien, leek het niet gepast bewijzen van anderen uit te geven met voorbijgaan van het zijne; maar het aan Neile over te laten dat van hem zelf uit te geven, of in elk geval een andere gelegenheid af te wachten.   1)  De tweede verhandeling van het boek van Wallis Tractatus duo, prior de Cycloide ... de Cissoide [zie bij No. 1946, noten 2 en 7], waaruit dit bewijs van Neile is gehaald, is geschreven in de vorm van een brief aan Huygens. [ Het blad met fig. 23 ontbreekt in het GWLB-exemplaar, dat in het bezit van Huygens is geweest.]   [ Getallenvoorbeeld: Neem AD = 4, DC = 2, dan is ADC = 16/3, zodat ADSI = 32/3, DS = 8/3, DH = 10/3, DHI = 36/3, en er komt AfC = 9/2, dus 4,5.  De rechte AC is hier 4,472...; de paraboolboog AbC is 4,878..., zie bij Wikipedia, Parabola: 'Length of an arc'.]

[ 339 ]

No 1960. Christiaan Huygens aan J. Wallis. 10 juli 1673 1). De brief is in Londen, Royal Society. Antwoord op No. 1947. Clarissimo et celeberrimo Viro D. Johanni Wallisio Chr. Hugenius. S. P.   Ik herken in uw recente brief uw uitnemende wellevendheid, zeer geleerde heer, wanneer u voor een zo kleine gift zo beleefd dankzegt, en terwijl deze rijk voorzien is van gewichtiger dingen vroeger van u afkomstig. Ik herken ook de gebruikelijke welwillendheid omdat u niet hebt geaarzeld aan te nemen dat het nog niet gelezen en nauwelijks ingeziene werkje zogezegd van enige waarde zou zijn. En als u deze mening nog hebt na afloop van het begonnen onderzoek, zal ik denken dat mijn werk in niet geringe mate vruchtbaar is geweest.   Maar wat de zaak Neile betreft, ik betreur het zeker als u hebt gemeend dat u op de een of andere manier van kwade trouw beschuldigd bent; daar dit geenszins kan worden opgemaakt uit wat ik heb geschreven, en geheel in strijd zou zijn met mijn bedoeling. In elk geval heb ik niets in twijfel getrokken van wat u vroeger over deze zaak in geschrifte openbaar hebt gemaakt. Maar ik heb vrijmoedig uiteengezet wat juist daaruit verzameld leek te kunnen worden, alleen geleid door het principe van onpartijdigheid, aangezien ik nog minder reden had waarom ik voor van Heuraet partij zou kiezen, dan u voor Neile, daar hij immers niet alleen mij weinig bekend was, maar zich ook niet zeer verdienstelijk had gemaakt voor mij 2).

Maar als het u hierna goed zal lijken die lof aan Neile toe te kennen, en wat er gedaan is verder uiteen te zetten, en ook voor uzelf aanspraak te maken op enig deel van die vondst, is er stellig niets wat het belet 3). Maar u ziet toch zelf voldoende in, dat getuigenissen van de uwen minder gewicht zullen hebben om te overtuigen, daar meestal wordt gedacht dat iedereen partij kiest voor zijn eigen volk. Terecht betreurt u het en spijt het u dat publicatie van de vondst in het begin is nagelaten; dit zou immers   1)  De brief was ingesloten bij die aan Oldenburg, No. 1959.   2)  Huygens maakt hier waarschijnlijk een toespeling op de brief van van Heuraet, gepubliceerd door van Schooten, waarover hij in zijn Horlogium oscillatorium spreekt in deze termen: "Cumque Schotenio ... absloute inveniuntur" [Ned.].

En toen we aan van Schooten, en evenzo aan anderen onder de vrienden, per brief hadden laten weten, dat twee ongewone vondsten over de parabool zich aan ons hadden voorgedaan, en dat een daarvan was het uitspannen van een conoïdisch oppervlak op een cirkel, heeft hij die brief gedeeld met van Heuraet, met wie hij toen vertrouwelijk omging. En voor deze, een zeer scherpzinnig iemand, was het niet moeilijk te begrijpen dat met het oppervlak van die conoïde verwant is de afmeting van die parabolische kromme. Toen hij beide vondsten daarna verder onderzocht, kwam hij op die andere parabolische krommen, waarbij volmaakt gelijke rechten worden gevonden.

Van Heuraet had in zijn brief niet gewezen op de samenhang van de ontdekkingen van Huygens en van hemzelf.   3)  Zie Aanhangsel No. 1961 [Wallis aan Oldenburg, 14 okt. 1673, in Phil. Trans., Numb. 98, Novemb. 17, 1673].

[ 340 ]

veel beter zijn geweest, dan het daarna te laat uit het verleden op te halen. En u kunt nu volstrekt niet zeggen dat dit van zo weinig belang is geweest, dat u zich er teveel op beroemd zou hebben, als u had gewild dat het zo spoedig mogelijk nadat het was gevonden in het licht zou komen en onder de aandacht van alle meetkundigen; anders zou immers een beetje roem ook nu als een teveel gezien moeten worden; maar, als ik de waarheid mag zeggen, uw Engelsen verlangen niet minder naar lof dan de Fransen of de Nederlanders, en dit is inderdaad vaker duidelijk gebleken 4). Doch het is er zover van verwijderd dat ik dit als iets verkeerds aanreken, dat ik denk dat het iets moois en voortreffelijks is, als aan de andere kant maar een ander opkomt tegen onrecht als iedereen zijn eigen roem bevordert. Iemand heeft gezegd dat door verachting hiervan de deugdzaamheid wordt veracht*), en wel terecht naar mijn gevoelen.   Maar hierover handel ik nu te uitgebreid, lijkt me, daar ik me had voorgesteld met deze brief slechts dit ene te bewerken, dat u mij niet iets zou aanrekenen dat onverdiend is en buiten mijn bedoeling, wat ik u hierbij dan ook dringend wil verzoeken°). Dat. Parisijs, 10 Julij 1672 5).   4)  Al in 1660 had Huygens aan de Carcavi geschreven: "Die meneer Wallis geeft er zeker blijk van een vlug verstand te hebben en het is vermakelijk te zien hoe hij uit alle macht de eer van zijn volk tracht te handhaven." Zie brief No. 735.   *)  [ Add. in T. VIII, p. 627:]  Tacitus, Annales IV, 38: "Contemptu famae contemni virtutes".   [ °)  Lat.: "te rogo, tum cupio" moet zijn "te rogatum cupio", zie The Correspondence of John Wallis (2014), p. 211.]   5)  Met deze brief eindigt de briefwisseling tussen Christiaan Huygens en John Wallis.

Phil. Trans. 15 (1685) Numb. 178.   *)  W. Oughtred, Key of the Mathematics (Lat. 1631), 1647 / 1694.