
Definities , cycloïde , parabool , ellips en hyperbool , elke meetkundige kromme
| [ 189 ] | (p. 59) |

H E T S L I N G E R - U U R W E R KD E R D E D E E L.Over afwikkeling & afmeting van kromme lijnen.
EEn lijn wordt naar één kant gebogen genoemd als alle rakende rechten haar aan dezelfde kant raken. En als enige gedeelten ervan rechte lijnen zijn, worden deze bij verlenging voor raaklijnen gehouden.
Wanneer nu twee van zulke lijnen van hetzelfde punt uitgaan, waarvan de bolling van de ene gekeerd is naar de holle kant van de andere, zoals in de hierbij getekende figuur de krommen ABC en ADE, worden beide naar dezelfde kant hol genoemd.
Als aangenomen wordt dat een lijn, naar een kant hol, is omwikkeld met een draad of buigzame lijn, en terwijl het ene uiteinde van de draad er aan vastgehecht blijft, wordt het andere uiteinde weggetrokken, zodanig dat het deel dat is vrijgemaakt steeds gestrekt blijft; dan is duidelijk dat door dit uiteinde van de draad een andere kromme wordt beschreven. En deze wordt genoemd de 'Door afwikkeling beschrevene'. [<] {p. 60}
En die kromme waar de draad omheen was gewikkeld, wordt genoemd 'Evoluut'. In bovenstaande figuur is ABC de evoluut, ADE de beschrevene dooer afwikkeling van ABC, namelijk zoals wanneer het uiteinde van de draad uit A in D komt, dan is het uitgestrekte deel van de draad de rechte DB, terwijl het overige deel BC nog bij de kromme ABC aansluit. Het is duidelijk dat DB dan de evoluut raakt in B.
|
[ 191 ] OVER AFWIKKELING VAN KROMME LIJNEN.
|
ELke rechte die de evoluut raakt ontmoet de door afwikkeling beschrevene onder rechte hoeken.
Omdat namelijk DC de evoluut raakt in D, blijkt deze de positie van de draad dàn weer te geven, wanneer het uiteinde daarvan in C komt. En als we dus hebben aangetoond dat de draad, bij de hele verdere beschrijving van de kromme ACH, zich nooit uitstrekt tot de rechte CE behalve in het punt C, zal duidelijk zijn dat de rechte CE daar de rechte ACH raakt. {p. 61}
Laat een of ander punt worden genomen op AC behalve C, dat H genoemd wordt, en laat het ten eerste verder van het begin van de afwikkeling A verwijderd zijn dan het punt C, en stellen we ons voor dat het vrije deel HG is, wanneer het met zijn uiteinde tot H komt. Dan raakt HG de lijn AB in G. En aangezien intussen, terwijl het deel van de kromme CH beschreven wordt, de boog DG wordt afgewikkeld, zal de aan de kant van D verlengde CD die HG ontmoeten, zoals in F. En stel dat GH de rechte CE ontmoet in E.
Laat nu het punt H dichter bij het begin van de afwikkeling A liggen dan punt C, en laat de positie van de draad zijn HG, toen het uiteinde daarvan in H was, en laat getrokken worden de rechten DG en DH, waarvan de laatste de rechte CE ontmoet in E; nu blijkt DG niet een rechte te kunnen zijn in de richting van HG, zodat HGD een driehoek zal zijn. Nu, omdat de rechte DG of kleiner is dan DKG, of hetzelfde, namelijk als het deel DG van de evoluut een rechte is; als aan beide wordt toegevoegd GH, zullen de rechten DG en GH samen kleiner zijn dan of gelijk aan deze twee, te weten DKG en GH, oftewel aan de rechte DC die eraan gelijk is. |
[ 193 ] OVER AFWIKKELING VAN KROMME LIJNEN. {p. 62}
|
En kleiner dan de twee rechten DG en GH is de rechte DH. Dus zal deze in elk geval kleiner zijn dan de rechte DC. Maar DE is groter dan DC, omdat in driehoek DCE hoek C recht is. Dus DH is veel kleiner dan DE. Dus is punt H, dat is het uiteinde van de draad GH, gelegen binnen driehoek DCE. Waaruit blijkt dat de draad zich ook nergens tussen A en C uitstrekt tot de rechte CE. Dus CE raakt de kromme AC in C; en zo ontmoet dus DC, waarop CE loodrecht is getrokken, de kromme onder rechte hoeken. Wat te bewijzen was. Hieruit is ook duidelijk dat de kromme AHC naar één kant gebogen is, en naar dezelfde kant hol als AGB, waarvan de afwikkeling is beschreven. Alle raaklijnen van de lijn AHC vallen immers buiten de ruimte DGAHC; maar alle raaklijnen aan de lijn AGD, binnen de genoemde ruimte. Waaruit blijkt dat de holle kant van AHC gericht is naar de bolling van AGD. ELke begrensde kromme lijn, naar één kant hol, zoals ABD, kan in zoveel delen worden verdeeld, dat als bij de afzonderlijke delen de koorden worden getrokken, zoals AB, BC, CD; en eveneens vanaf afzonderlijke punten van de verdeling, en vanaf een uiteinde van de kromme, rechten worden getrokken die de kromme raken, zoals AN, BO, CP, lopend tot aan de lijnen die loodrecht op de kromme staan in de eerstvolgende verdeelpunten, zoals de lijnen BN, CO, DP; zoveel delen zeg ik, dat elke koorde een verhouding heeft tot de aanliggende lijn loodrecht op de kromme, zoals AB tot BN, BC tot CO, CD tot DP, die groter is dan ieder mogelijke voorgestelde verhouding. Laat namelijk gegeven zijn de verhouding van de lijn EF tot FG, die bij F onder een rechte hoek worden verbonden, en trek de rechte GEH. |
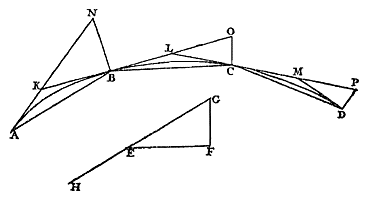
| Stel dat de kromme eerst in zo kleine delen wordt gesneden met punten B en C, dat de raaklijnen die bij elke twee het dichtst bij elkaar liggende punten de kromme raken, elkaar ontmoeten volgens hoeken die elk afzonderlijk groter zijn dan de hoek FEH; zoals de hoeken AKB, BLC en CMD. En dat gedaan kan worden is zo duidelijk dat het geen bewijs |
[ 195 ] OVER AFWIKKELING VAN KROMME LIJNEN.
|
nodig heeft. Als nu de koorden AB, BC en CD getrokken zijn, en loodrecht op de kromme opgericht BN, CO en DP, die de verlengden van AK, BL en CM ontmoeten in N, O en P: dan zeg ik dat de afzonderlijke verhoudingen van de rechten, AB tot BN, BC tot CO en CD tot DP, groter zijn dan de verhouding van EF tot FG. {p. 63} Immers, omdat hoek AKB groter is dan hoek HEF, zal het supplement van de eerste, namelijk hoek NKB, kleiner zijn dan hoek GEF. En hoek B van driehoek KBN is recht, zoals ook hoek F in driehoek EFG. Dus de verhouding van KB tot BN zal groter zijn dan die van EF tot FG. Maar AB is groter dan KB, aangezien hoek K in driehoek AKB stomp is, hij is immers groter dan hoek HEF die door constructie stomp is. Dus de verhouding van AB tot BN zal groter zijn dan de verhouding van KB tot BN, en zo dus in elk geval groter dan de verhouding van EF tot FG. Op dezelfde manier wordt ook aangetoond dat de verhouding van BC tot CO, en van CD tot DP, groter is dan de verhouding van EF tot FG. Daarom staat het voorgestelde vast. TWee krommen die naar één kant gebogen zijn en naar dezelfde kant hol, kunnen niet uit hetzelfde punt weggaan in een zodanige positie ten opzichte van elkaar, dat elke rechte die één ervan onder rechte hoeken ontmoet, evenzo ook de andere ontmoet. Laat namelijk, als het mogelijk is, twee van zulke kromme lijnen zijn ACE en AGK, die als gemeenschappelijk uiteinde A hebben, en laat op de buitenste daarvan genomen worden een willekeurig punt K, met vandaar een rechte KE getrokken, die de kromme AGK onder rechte hoeken ontmoet, en zo dus ook de kromme ACE. {p. 64} |
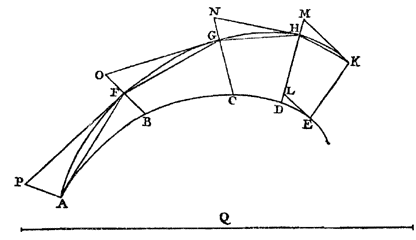
| Nu kan een of andere rechte genomen worden die groter is dan de kromme KGA, bijvoorbeeld Q. En aangenomen wordt dat die KGA is verdeeld, zoals in de voorgaande propositie is gezegd, in zoveel delen met punten H, G en F, dat de afzonderlijke koorden KH, HG, GF en FA tot de eraan grenzende loodlijnen op de kromme HM, GN, FO en AP een grotere verhouding hebben dan de lijn Q tot de rechte KE. Dientengevolge zullen ook alle genoemde koorden samen tot alle genoemde loodlijnen een grotere verhouding hebben dan van Q tot KE. Laat nu die loodlijnen worden verlengd en |
[ 197 ] OVER AFWIKKELING VAN KROMME LIJNEN.
|
de kromme ACE ontmoeten in D, C en B, en wel onder rechte hoeken volgens de hypothese. Nu zal KE kleiner zijn dan MD. Immers, als EL loodrecht op die KE is getrokken zal EL de kromme ACE raken, aangezien KE de kromme lijn ECA onder rechte hoeken onmoet, en EL zal noodzakelijk de rechte MD tussen D en M ontmoeten. Waaruit volgt, daar KE de kortste is van alle lijnen die vallen tussen de evenwijdigen EL en KM, dat deze kleiner zal zijn dan ML, en zo dus ook in elk geval kleiner dan MD. Op dezelfde manier wordt ook aangetoond dat HD kleiner is dan NC, en GC kleiner dan OB, en FB kleiner dan PA. Aangezien dus PA groter is dan FB, zullen de twee samen PA en OF groter zijn dan OB. Evenzo, daar OB groter is dan GC, zullen de twee samen OB en NG groter zijn dan NC. Maar de twee PA en OF waren groter dan OB. Dus de drie samen PA, OF en NG zullen in elk geval groter zijn dan NC. Nog eens, omdat NC groter is dan HD, zullen de twee samen NC en MH groter zijn dan MD. Waaruit volgt, als in plaats van NC de drie groter dan deze genomen worden, PA, OF en NG, dat in elk geval deze vier PA, OF, NG en MH groter zullen zijn dan MD. En zo zijn deze dus in elk geval ook groter dan de rechte KE, omdat MD groter was dan KE. Nu hebben we gezegd dat alle koorden AF, FG, GH en HK een grotere verhouding hebben tot alle loodlijnen PA, OF, NG en MH, dan de lijn Q tot KE. Dus daar KE nog kleiner is dan de genoemde loodlijnen, zullen de genoemde koorden tot KE in elk geval een grotere verhouding hebben dan Q tot KE. Dus de koorden samen genomen zullen groter zijn dan de rechte Q. En deze was groter genomen dan de kromme AGK. Dus de koorden AF, FG, GH en HK zullen samen groter zijn dan dan de kromme AGK waarvan ze de delen onderspannen; wat absurd is, daar ze elk kleiner zijn dan hun boog. Dan zullen er niet twee kromme lijnen kunnen zijn die een positie hebben zoals gezegd is. Wat te bewijzen was. ALs vanaf hetzelfde punt twee lijnen weggaan die naar één kant gebogen zijn en naar dezelfde kant hol, en in een zodanige onderlinge positie dat alle rechten, die één ervan raken, de andere ontmoeten onder rechte hoeken, zal deze laatste beschreven worden door afwikkeling van de eerste, begonnen in het gemeenschappelijke punt. {p. 65} Gegeven de lijnen ABC en ADE, naar één kant gebogen, en waarvan elke naar dezelfde kant hol is, en ze hebben een gemeenschappelijk eindpunt A. En alle rechten die de lijn ABC raken, zoals BD en CE, ontmoeten de lin ADE onder rechte hoeken. Ik zeg dat door afwikkeling van ABC, te beginnen bij het uiteinde A, wordt beschreven ADE. |
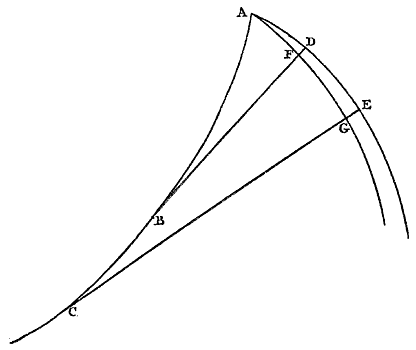
| Laat namelijk als het mogelijk is, door de genoemde afwikkeling een andere kromme AFG worden beschreven. Dan zullen rechte lijnen, welke dan ook, die de evoluut ABC raken, zoals BD en CE, deze AFG ontmoeten onder rechte hoeken {Prop. 1.}, neem aan in F en G. Maar gesteld wordt dat dezelfde raaklijnen ook de lijn ADE onder rechte hoeken ontmoeten. Dus de kromme lijnen ADE en AFG eindigen in hetzelfde punt A, en ze zijn naar één kant gebogen, en beide naar dezelfde kant hol, elke immers |
[ 199 ] OVER AFWIKKELING VAN KROMME LIJNEN.
|
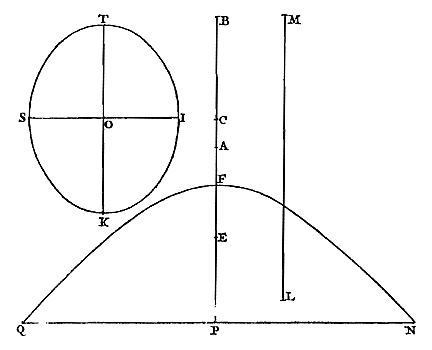
naar dezelfde kant als ABC; want van lijn ADE staat het volgens de hypothese vast, en van AFG volgens de eerste propositie hierboven; en alle rechten die één ervan ontmoeten onder rechte hoeken, ontmoeten ook de andere evenzo. En eerder is aangetoond {Prop. 3.} dat dit niet zo kan zijn. En daarom staat vast dat ADE beschreven zal worden door afwikkeling van de lijn ABC. Wat te bewijzen was. {p. 66} ALs aan een cycloïde in de top een rechte raakt, en met deze als basis wordt een andere dergelijke en gelijke cycloïde er op geplaatst, een begin nemend vanuit het genoemde toppunt, dan zal iedere rechte die de onderste cycloïde raakt, het gedeelte van de bovenste dat daarop is geplaatst onder rechte hoeken ontmoeten. 1) Laat aan de cycloïde ABC in de top A de rechte AG raken [Fig. 58], en met deze als basis wordt nog een dergelijke cycloïde AEF er op geplaatst, waarvan de top F is. En aan de cycloïde ABC raakt de rechte BK in B. Ik zeg dat deze bij verlenging de cycloïde AEF onder rechte hoeken ontmoet. |
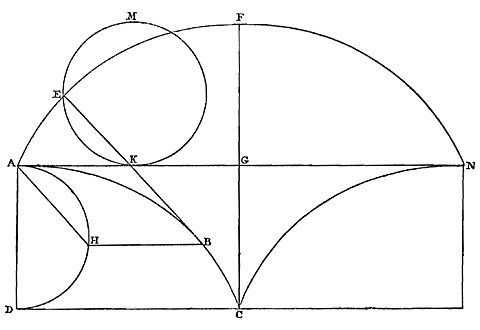
|
Laat namelijk rondom AD, de as van cycloïde ABC, de voortbrengende cirkel AHD beschreven worden, die door BH, evenwijdig met de basis, wordt ontmoet in H, en trek HA. Omdat dus BK de cycloïde raakt in B, staat vast dat deze evenwijdig is met de rechte HA {Prop. 15 van deel 2.}. Dus AHBK is een parallelogram, en zo is dus AK gelijk aan HB, dat is, aan de boog AH {Prop. 14 van deel 2.}. Laat nu verder beschreven zijn de cirkel KM, gelijk aan de voortbrengende cirkel, dat is AHD, die de basis AG raakt in K, en die de verlengde
1) Vergelijk over deze en de volgende propositie p. 404-405 van T. XIV en 142-145 van T. XVII. |
[ 201 ] OVER AFWIKKELING VAN KROMME LIJNEN.
|
rechte BK snijdt in punt E. Omdat dus met AH evenwijdig is BKE, en zo dus hoek EKA gelijk aan KAH, is duidelijk dat de verlengde van BK, van cirkel KM een boog afsnijdt gelijk aan die welke van cirkel AHD wordt afgesneden door de rechte HA. En hieruit volgt, uit de eigenschap van de cycloïde, dat toen de voortbrengende cirkel MK de lat [<] raakte in K, het beschrijvende punt in E was. Dus de rechte KE ontmoet de cycloïde in E onder rechte hoeken {Prop. 15 van deel 2.}. Nu is KE de verlengde van BK. Dus blijkt dat de verlengde BK de cycloïde onder rechte hoeken ontmoet. Wat te bewijzen was. {p. 67} Door afwikkeling van een halve cycloïde, te beginnen bij de top, wordt een andere cycloïde beschreven die gelijk en gelijkvormig is met de evoluut, waarvan de basis is op de rechte die de afgewikkelde cycloïde raakt in de top.
Gegeven de halve cycloïde ABC, waarop geplaatst is een andere dergelijke AEF, zoals in de vorige propositie [Fig. 58]. Ik zeg: als een buigzame lijn, aansluitend tegen de halve cycloïde ABC, wordt afgewikkeld, beginnend bij A, beschrijft deze met het uiteinde de halve cycloïde AEF. |
[ 203 ] OVER AFWIKKELING VAN KROMME LIJNEN.
| En het blijkt, als we een andere halve cycloïde, de tweelinghelft van ABC, in tegengestelde positie vanaf de andere kant van de lijn CG opstellen, zoals CN, dat door afwikkeling hiervan, of ook wanneer de draad, al uitgestrekt naar CF, erom opgewikkeld wordt, door het uiteinde van de draad een andere halve cycloïde FN zal worden beschreven, die samen met de vorige AEF een hele tot stand brengt. |
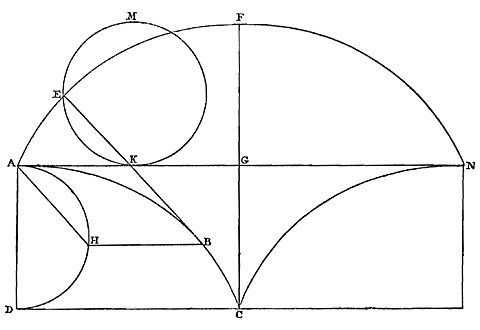
|
En hieruit, en uit propositie 25 van 'Over het dalen van wat zwaarte heeft', is nu duidelijk wat hierboven bij de Constructie van het Uurwerk is gezegd over de gelijkmatige beweging van een slinger [<]. Het blijkt namelijk dat een schietlood, tussen twee volgens een cycloïde gebogen plaatjes opgehangen en in beweging gezet, bij zijn beweging een cycloïde-boog beschrijft, en dus ook dat alle mogelijke bewegingen heen en weer in gelijke tijden worden uitgevoerd. Het maakt immers niet uit of een voorwerp op een volgens een cycloïde gebogen oppervlak beweegt, of vastgemaakt aan een draad die lijn in de lucht doorloopt, aangezien het in beide gevallen dezelfde vrijheid heeft, en in alle punten van de kromme dezelfde neiging om te bewegen. {p. 68} DE cycloïde-lijn is het viervoudige van zijn as, of van de middellijn van de voortbrengende cirkel. Zie de vorige figuur [Fig. 58]: aangezien na afwikkeling van de gehele halve cycloïde ABC de draad de rechte CF beslaat; die het dubbele is van AD, omdat de assen van de cycloïden ABC en AEF gelijk zijn; blijkt de halve cycloïde ABC, die gelijk is aan de draad als deze erom gewikkeld is, het dubbele van zijn as AD te zijn, en zo dus de hele cycloïde het viervoudige van zijn as. Het blijkt ook dat de raaklijn BE, die het uitgestrekte deel van de draad weergeeft dat tevoren bij deel BA van de kromme aansloot, gelijk is aan deze laatste lengte. BE is namelijk het dubbele van BK, of AH, aangezien in de vijfde propositie is aangetoond dat KE gelijk is aan AH. Dus het deel AB van de cycloïde zal het dubbele zijn van de rechte AH, of BK; BH is immers evenwijdig aan de basis van de cycloïde. En dit is zo, waar ook op de cycloïde het punt B wordt genomen. Dit afmeten van de cycloïde is het eerst gevonden, langs een wel lange andere weg, door de uitmuntende Engelse meetkundige Christopher Wren 1), en daarna heeft hij het bevestigd met een elegant bewijs, dat is uitgegeven in het boek over de cycloïde van de zeer beroemde heer John Wallis 2). En over dezelfde lijn zijn ook voorhanden vele andere zeer mooie vondsten van wiskundigen van onze tijd, waartoe vooral aanleiding gaven enige problemen [<] voorgesteld door de Fransman Blaise Pascal, die in deze studies uitblonk. In een overzicht van zowel zijn vondsten als die van anderen 3) zegt hij dat Mersenne als eerste van allen deze lijn in de natuur heeft opgemerkt 4). 1) Vergelijk p. 203 van T. XIV en noot 3 van p. 145 van T. XVII. 2) Zie over dit werk noot 3 van p. 518 van T. II [Tractatus Duo. Prior, de cycloide ..., 1659, p. 77]. 3) In zijn Histoire de la Roulette van 1658 (noot 4 van p. 350 van T. XIV). Zie ook zijn 'Lettre de A. Dettonville a Monsieur Hugguens de Zulichem' van februari 1659 (p. 196 van T. XIV). 4) C. de Waard, uitgever van de Correspondance du P. Marin Mersenne (zie noot 8 van p. 41 hiervoor) schrijft op p. XXV van zijn 'Notitie over het leven van Mersenne', waarmee deel 1 begint: "Het is gedurende dit verblijf [in het klooster van de Place Royale te Parijs], volgens Pascal en sommige andere geleerden, dat Mersenne in 1615 de vorm van de cycloïde had gevonden, maar het ging op dit moment ongetwijfeld slechts om een studie naar het wiel van Aristoteles, een probleem waarover toen veel werd gedebatteerd" [<]. Toch is ook de Waard van mening dat het Mersenne was die als eerste het probleem van de cycloïde stelde: "om te geloven dat het door studie van het wiel van Aristoteles was dat Mersenne omstreeks 1615 ertoe werd gebracht het probleem van de cycloïde te bestuderen, hebben we minstens zo sterke redenen als om geloof te hechten aan het wat gekleurde verhaal van Pascal" ('Une lettre inédite de Roberval du 6 janvier 1637 contenant le premier énoncé de la cycloïde' [suite] door C. de Waard, Bulletin des Sciences Math., red. E. Picard en P. Appell, Serie II, T. XLV, Paris, 1921). |
[ 205 ] OVER AFWIKKELING VAN KROMME LIJNEN. {p. 69}
|
Dat Roberval als eerste de raaklijnen ervan heeft bepaald, en ook vlakken en lichamen heeft afgemeten. Dat hij eveneens zwaartepunten heeft gevonden van zowel vlakke als vaste delen ervan. Dat Wren als eerste een rechte heeft gegeven die gelijk is aan de cycloïde-kromme. Ook dat ik als eerste heb gevonden de volledige afmeting van het gedeelte van de cycloïde, dat door een rechte evenwijdig met de basis wordt afgeneden, door een punt van de as dat op een vierde deel ervan van de top af ligt; dit gedeelte is namelijk gelijk aan een halve gelijkzijdige zeshoek, binnen de voortbrengende cirkel beschreven 1). Dat hijzelf tenslotte zwaartepunten heeft bepaald van lichamen en ook halve lichamen, zowel om de basis als om de as, en eveneens van hun delen. Dat hij ook van de lijn zelf (maar dit na de afmeting van Wren ontvangen te hebben) het zwaartepunt heeft gevonden, en de afmeting van bolle oppervlakken, waardoor die lichamen en hun delen worden omvat; en van hun oppervlakken de zwaartepunten. En tenslotte ook de afmeting van alle mogelijke cycloïdale krommen, zowel verlengd als verkort; dat is van die welke worden beschreven door een punt binnen of buiten de omtrek van de genomen voortbrengende cirkel [^]. En althans hiervan zijn bewijzen uitgegeven door Pascal. Waarna ook de heer Wallis over dezelfde lijn zijn zeer subtiele gedachten heeft uiteengezet, en hij verzekert dat hij dat alles zelfstandig heeft gevonden, en ook dat hij de door Pascal voorgelegde problemen heeft opgelost. En ook de zeer geleerde Lalovera maakt aanspraak op hetzelfde 2). En hoeveel aan elk is verschuldigd, moeten de geleerden op grond van hun geschriften beslissen. We hebben het voorgaande slechts verteld, omdat ons leek dat niet in stilte voorbijgegaan mocht worden aan zulke uitstekende vondsten, waardoor het een feit is dat onder alle lijnen, geen nu beter of vollediger bekend is dan de cycloïde. 1) T. XIV, p. 350-351 (1658). 2) Zie over de oplossingen van A. de la Loubère noot 6 van p. 346 van T. II. [Propositio 36, 1659; Veterum geometria promota, 1660.] |
[ 207 ] OVER AFWIKKELING VAN KROMME LIJNEN.
|
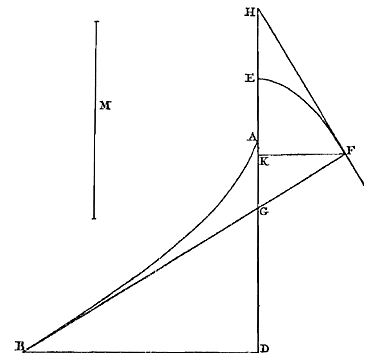
En onze methode, die we bij het afmeten van deze lijn gebruikten, hebben we ook willen proberen bij andere, waarover we nu zullen handelen. AAn te tonen door afwikkeling van welke lijn een parabool wordt beschreven. 1)
Gegeven een parabolische kromme AB, met as AD, en top A [Fig. 59]; met deze eigenschap dat, met BD als ordinaat op de as gezet, de derde macht van de abscis DA tot de top gelijk is aan een lichaam met als basis het kwadraat van DB, en waarvan de hoogte gelijk is aan een zekere gegeven lijn M; deze kromme was aan meetkundigen al lang bekend; en laat met de as DE recht zijn samengevoegd AE, gelijk aan 8/27 van M. |
|
Genomen namelijk op de kromme AB een willekeurig punt B, moet de rechte BG worden getrokken die in dit punt de kromme raakt, de as EA ontmoetend in G; en verder wordt uit G getrokken GF, die de parabool EF onder rechte hoeken ontmoet in F; en deze GF staat loodrecht op FH, die de parabool in F raakt; en tenslotte wordt FK als ordinaat op de as gezet. Dan is KG*) gelijk aan de helft van het latus rectum, dat is aan EA; en zo dus, als bij beide AK is toegevoegd of weggenomen, zal EK gelijk zijn aan AG. Nu is AG een derde van AD, aangezien BG de parabolische kromme raakt in B; dat kan namelijk uit de aard van deze kromme gemakkelijk bewezen worden. Dus ook EK is gelijk aan een derde van AD; en KH, die volgens de aard van de parabool het dubbele is van KE, zal gelijk zijn aan twee derde van AD. Dus de derde macht van KH is gelijk aan 8/27 van de derde macht van AD, dat is aan het lichaam dat als basis heeft het vierkant DB, en de hoogte gelijk aan 8/27 M, dat is, aan AE. En daarom geldt: zoals het kwadraat van DB tot het kwadraat van KH, zo zal zijn lengte KH tot AE, dat is tot KG. En KH was gelijk aan 2/3 AD, dat is aan GD. Dus zoals het kwadraat van BD tot het kwadraat van DG, zo is HK tot KG. En zoals HK tot KG, zo is het kwadraat van FK tot het kwadraat van KG°). Dus zoals het kwadraat van BD is tot het kwadraat 1) Zie over de algemene methode om de vorm van evoluten te vinden Prop. XI hierna. De evoluut van de gewone parabool, evenals die van parabolen en hyperbolen van hogere graad, waren aan Huygens al bekend sedert december 1659; zie de noten 2 en 3 van p. 147 van T. XVII.  [ *) KG heet 'subnormaal', en is gelijk aan de 'parameter' van de parabool.]
[ *) KG heet 'subnormaal', en is gelijk aan de 'parameter' van de parabool.][ °) Omdat in de rechthoekige driehoek GFH geldt: FK² = HK.KG.] [ Figuur: de omhullingscurve van de normalen op een parabool is een semi-kubische parabool, in Pythagoras 8-2 (1968-69), p. 30. NB: Het in het Latijn gebruikte 'paraboloides' betekent: parabool-achtige; Huygens gebruikt ook 'curva parabolica' (p. 211, 219). Nu is een paraboloïde een kwadratisch oppervlak in drie dimensies.] |
[ 209 ] OVER AFWIKKELING VAN KROMME LIJNEN.
|
van DG, zo is het kwadraat van FK tot het kwadraat van KG. En daarom zoals BD tot DG in lengte, zo is FK tot KG. Waaruit volgt dat BGF een rechte lijn is. Maar GF ontmoet de parabool EF onder rechte hoeken. Dus blijkt BG, de raaklijn aan de parabolische kromme, na verlenging die parabool te ontmoeten onder rechte hoeken. En dit is evenzo te bewijzen over elke mogelijke raaklijn eraan. Dus staat vast dat door afwikkeling van de lijn EAB, vanaf het uiteinde E begonnen, de parabool EF wordt beschreven {Prop. 4}. Wat te bewijzen was. {p. 71} EEn rechte te lijn vinden gelijk aan een gegeven gedeelte van een parabolische kromme, namelijk van die waarbij de kwadraten van ordinaten op de as, zich tot elkaar verhouden zoals de derde machten van de abscissen tot de top.
|
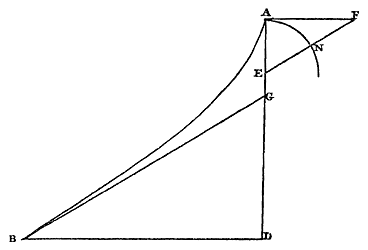
|
Hoe dit gedaan wordt is duidelijk uit de vorige propositie. De parabool EF [Fig. 59] is echter niet vereist voor de constructie, die als volgt te volbrengen is. Gegeven een of ander deel van deze parabolische kromme AB [Fig. 60] waarbij een gelijke rechte moet worden gevonden, wordt getrokken BG, raaklijn in punt B, die de as AG ontmoet in G. En hij zal raken als AG een derde deel is van AD, onderschept tussen de top en de ordinaat BD. Verder, met AE genomen gelijk aan 8/27 van de lijn M, die het latus rectum is van de parabolische kromme AB, wordt getrokken EF evenwijdig aan BG, en hij ontmoet de lijn AF, die evenwijdig is met BD, in F. Als nu bij de rechte BG wordt gevoegd NF, het overschot van EF boven EA, zal men de rechte hebben die gelijk is aan de kromme AB. Waarvan het bewijs gemakkelijk is in te zien op grond van wat eerder gezegd is.*) Steeds overtreft dus de kromme AB de raaklijn zoveel, als de rechte EF de rechte EA. En weer zijn we hier terechtgekomen bij een lijn waarvan anderen de lengte al eerder hebben afgemeten. Namelijk die waarvan Joh. [Hendrik] van Heuraet van Haarlem in 1659 heeft aangetoond dat ze gelijk is aan een rechte, en zijn bewijs is toegevoegd aan de commentaren van Joh. [Frans] van Schooten op de Geometria van Descartes, in hetzelfde jaar uitgegeven. En hij heeft wel als eerste van allen een kromme lijn, van de soort waarvan willekeurige punten meetkundig worden bepaald, tot deze afmeting herleid, toen Wren omstreeks dezelfde tijd de lengte van de cycloïde had gegeven, met een niet minder ingenieuze aanpak. [ *) In fig. 59 is de kromme AB = BG + GF – AE, en driehoek KGF (met KG = AE) is congruent met driehoek AEF in fig. 60.] |
[ 211 ] OVER AFWIKKELING VAN KROMME LIJNEN. {p. 72}
|
Ik weet inderdaad dat, nadat de vondst van van Heuraet was uitgegeven, de zeergeleerde Wallis die heeft willen toekennen aan William Neile, een jonge edelman en landgenoot, in het boek over de Cissoïde*). Maar mij lijkt, als ik nauwkeurig afweeg wat hij daar aanvoert, dat Neile zeker niet ver van die vondst af is geweest, maar toch deze niet geheel heeft bereikt. Want het blijkt ook niet uit zijn bewijs, dat Wallis aanvoert, dat hij voldoende doorzien heeft wat voor kromme dat zou zijn, waarvan hij zag dat de afmeting gegeven zou worden als ze geconstrueerd werd. En als hij had geweten dat het een van de krommen was die al lang bij de meetkundigen bekend waren, is te geloven dat of hij zelf, of anderen uit zijn naam, tijdiger mededeling hadden gedaan aan de meetkundigen van een zo edele vondst, die meer dan iets anders verdiende dat ze het Archimedische heureka zouden uitroepen. Het is zeker dat van deze vondst, als een eigen bijdrage, ook Fermat, senator in Toulouse en ook zeer bedreven in de meetkunde, bewijzen heeft opgeschreven, die in 1660 gedrukt zijn, maar die zijn in elk geval te laat 1). En nu we het hierover hebben, zij het ons vergund ook te spreken over wat wij hebben bijgedragen aan het bevorderen van een zo uitstekende vondst: aangezien wij èn aan van Heuraet de aanleiding hebben gegeven om zo ver te komen, èn vóór hem als eerste van allen hebben gevonden de afmeting van een parabolische kromme uit de gegeven kwadratuur van een hyperbool, die een deel is van Heuraet's vondst. Tegen het einde van het jaar 1657 zijn we namelijk op de volgende twee dingen tegelijk gekomen, de genoemde afmeting van een parabolische kromme, en de herleiding van het oppervlak van een parabolische conoïde tot een cirkel. En toen we aan van Schooten, en evenzo aan anderen onder de vrienden, per brief hadden laten weten, dat twee ongewone vondsten over de parabool zich aan ons hadden voorgedaan, en dat een daarvan was het uitspannen van een conoïdisch oppervlak op een cirkel, heeft hij die brief gedeeld met van Heuraet, met wie hij toen vertrouwelijk omging. En voor deze, een zeer scherpzinnig iemand, was het niet moeilijk te begrijpen dat met het oppervlak van die conoïde verwant is de afmeting van die parabolische kromme. Toen hij beide vondsten daarna verder onderzocht, kwam hij op die andere parabolische krommen, waarbij volmaakt gelijke rechten worden gevonden 2). En althans over het herleiden van het oppervlak van een conoïde tot een vlak, opdat niet misschien iemand een getuigenis mist, leek het goed hier het volgende te citeren uit een brief van de illustere heer, die beschouwd kan worden te behoren tot de voornaamste meetkundigen van deze tijd, [René] Franc. de Sluse, waarin hij mij in hetzelfde jaar feliciteerde met die vondst, en misschien wel uitgebreider dan verdiend was. Deze brief, gedateerd op 24 december 1657 3), bevat het volgende: Slechts twee dingen heb ik toe te voegen: het ene is ... enz. Het andere is dat voor mij [ *) J. Wallis, Tractatus duo ... De Cissoide (1659), p. 90 e.v., fig.; GLWB-ex. met marginalia van Huygens op p. 95-99.] 1) Zie over de kwestie v. Heuraet-Neile noot 2 van p. 123 van T. XVII. Huygens was blijkbaar al in 1660 van plan erover te spreken toen ze nog actueel was. De verschijning van Hor. osc. gaf aanleiding tot een discussie over dit onderwerp (o. a. met Wallis), zie T. VII [p. 306 e.v.]. In een brief aan Leibniz van 1 dec. 1686 schrijft Wallis (p. 653 van T. III van zijn Opera mathematica, Oxford 1699): "Over de vondst van Neile die (zich baserend op het door mij geleverde bij Prop. 38 van Ar. Infinitorum) als eerste van allen een rechte gelijk aan een kromme heeft laten zien: wat Huygens had gezegd (dat hij er niet ver vanaf was geweest, het echter niet geheel had bereikt) dat heeft Huygens later teruggetrokken (in een brief van hem aan mij) en gezegd dat ik het weer aan Neile moest toekennen. Of Neile meteen helemaal heeft geweten hoe deze kromme was, weet ik niet zeker. Maar Brouncker en ik hebben onmiddellijk ontdekt dat het een parabolische kromme is, waarvoor ik de naam 'semikubische' heb gemaakt." We kennen geen brief van Huygens aan Wallis waar hij de mening uitgedrukt in Horologium oscillatorium intrekt. 2) Zie p. 189-190 en 196 van T. XIV. [Ned.: brief aan de Sluse, 20 dec. 1657. Vergelijk: figuur van 1646.] 3) T. II, p. 107. |
[ 213 ] OVER AFWIKKELING VAN KROMME LIJNEN. {p. 73}
|
al die krommen, en zelfs die gehele lineaire plaats, bijna niets betekenen in vergelijking met deze vondst van u, waarmee u de verhouding hebt bewezen van een oppervlak op een parabolische conoïde tot de cirkel die de basis ervan is. Deze afleiding, een heel mooi vertrekpunt voor een kwadratuur van de cirkel, stel ik graag boven al die dingen, die ik eertijds heb afgeleid uit een lineaire meetkundige plaats, het waren er niet weinig, en zo u wilt zal ik ze met u delen als de gelegenheid zich voordoet. En het jaar daarna heb ik ook oppervlakken van hyperbolische en sferoïdische conoïden gevonden, hoe ze tot cirkels herleid konden worden, en de constructies van problemen erover heb ik, evenwel zonder het bewijs toe te voegen, meegedeeld aan meetkundigen met wie ik toen een briefwisseling had, in Frankrijk aan Pascal en anderen, in Engeland aan Wallis, die niet lang daarna ook zijn subtiele vondsten hierover, samen met veel andere, in het licht gaf, en maakte dat ik er van afzag onze bewijzen te voltooien 1). Aangezien nu onze constructies niet onelegant leken, en ze nog niet zijn gepubliceerd, wil ik ze op deze plaats toevoegen.
Na verlenging van de as aan de kant van de top, wordt genomen BE gelijk aan BD, en getrokken wordt EA, die de parabool ABC in A raakt. Verder wordt AD verdeeld in G, zodat AG tot GD is zoals EA tot AD. En gelijk aan beide AE en DG samen wordt een rechte H opgetrokken. Evenzo zij gelijk aan een derde van de basis AC de rechte L, en tussen H en L wordt de middelevenredige K gevonden, waarmee als straal een cirkel wordt beschreven. Deze zal gelijk zijn aan het gebogen oppervlak van de conoïde ABC.
Stel DF gelijk aan CB, of stel dat F een van beide brandpunten is van de ellips ADBE, en trek aan de rechte FD evenwijdig BG, die de verlengde ED ontmoet in G, en beschrijf met als middelpunt G en straal GB op de as AB een cirkel met omtrek BHA. 1) Vergelijk p. 192 van T. XIV [en zie Wallis, Tractatus duo (1659), p. 98, 103]. 2) Zie p. 267-268 van T. XIV. 3) Zie p. 190 en 320-324 van T. XIV. |
[ 215 ] OVER AFWIKKELING VAN KROMME LIJNEN.
|
En neem de rechte K als middelevenredige tussen de halve middellijn CD en de rechte, gelijk aan deze twee, boog AHB en middellijn DE. Dan zal K de straal zijn van de cirkel die gelijk is aan het oppervlak van de sferoïde ADBE. {p. 75}
Laat weer F een van beide brandpunten zijn, en als FC in G doormidden is gedeeld, stellen we ons voor de parabool AGB die als basis heeft de as AB, en als top het punt G. En neem middelevenredig tussen de middellijn DE, en de rechte die gelijk is aan de parabolische kromme AGB, de lijn H.
Gegeven een hyperbolische conoïde waarvan de as AB is, een doorsnede door de as de hyperbool CAD, waarvan het latus transversum EA is, het middelpunt F, het latus rectum AG.*) |
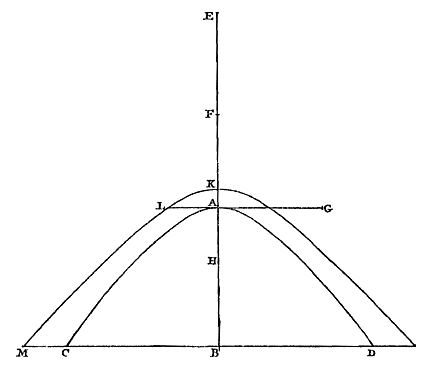
|
Neem op de as de rechte AH, gelijk aan de helft van het latus rectum AG, en zoals HF tot AF in lengte,
1) Zie p. 317-319 van T. XIV. 2) Zie p. 315-316 van T. XIV. [ *) Latus rectum: lengte van de koorde door een brandpunt loodrecht de op as; latus transversum: van top naar top.] [^] |
[ 217 ] OVER AFWIKKELING VAN KROMME LIJNEN.
|
zo moet zijn het kwadraat van AF tot FK. En we stellen ons voor dat met als top K een andere hyperbool KLM is beschreven, met dezelfde as en middelpunt F als de vorige, en die het latus rectum en transversum in omgekeerde verhouding heeft met de vorige. De verlengde BC ontmoet deze in M, en AL is evenwijdig met BC. Nu zal gelden: zoals de ruimte ALMB, door drie rechte lijnen en een hyperbolische kromme omvat, is tot het halve kwadraat van BC, zo is het gebogen oppervlak van de conoïde tot de cirkel van zijn basis, waarvan de middellijn CD is. Waaruit volgt dat de rest van de constructie gemakkelijk is af te maken, gesteld de kwadratuur van de hyperbool. Terwijl dus het oppervlak van een parabolische conoïde tot een cirkel wordt herleid, evenals het oppervlak van een bol, volgens bekende meetkundige regels, moet bij het oppervlak van een langwerpige sferoïde, om hetzelfde te doen, gesteld worden dat de lengte van een omtreksboog gelijkgesteld kan worden aan een rechte lijn. En om het oppervlak van een wijde sferoïde, en eveneens dat van een hyperbolische conoïde, te herleiden tot een vlak, wordt de kwadratuur van de hyperbool vereist. Want de lengte van een parabolische lijn, die we bij deze sferoïde gebruikten, is afhankelijk van de kwadratuur van de hyperbool, zoals we dadelijk zullen aantonen. {p. 76} Maar, wat wel de aandacht waard lijkt, we hebben zonder enige veronderstelling over de kwadratuur van de hyperbool gevonden, hoe een cirkel te construeren die gelijk is aan het oppervlak van beide samen, een wijde sferoïde en een hyperbolische conoïde. Gegeven namelijk een of andere wijde sferoïde kan een hyperbolische conoïde worden gevonden, of omgekeerd, gegeven een hyperbolische conoïde kan een wijde sferoïde worden gevonden, zodanig dat een cirkel kan worden gegeven die gelijk is aan het oppervlak van beide samen 1). Het zal voldoende zijn een voorbeeld hiervan aan te voeren in een geval dat eenvoudiger is dan andere. Laat gegeven zijn een wijde sferoïde waarvan de as SI is, een doorsnede door de as de ellips STIK, van welke ellips het middelpunt is O, de grote as TK. Stel nu dat deze ellips zodanig is dat het latus transversum TK tot het latus rectum dezelfde verhouding heeft, als een lijn die verdeeld is volgens uiterste en middelste reden [^], tot het grootste deel ervan. |
|
Neem het kwadraat van BC gelijk aan het dubbele van het kwadraat van SO, evenzo het kwadraat van BA aan het dubbele van dat van OK. En laat deze vier evenredig zijn BC, BA, BF, BE, en stel EP gelijk aan EA. We stellen ons nu voor de hyperbolische conoïde QFN, met de as FP; het aan de as toegevoegde,
1) T. XIV, p. 192-195, 324-326, 329-334. |
[ 219 ] OVER AFWIKKELING VAN KROMME LIJNEN. {p. 77}
|
of ½ latus transversum FB; de helft van het latus rectum is gelijk aan BC. Het gebogen oppervlak van deze conoïde, samen met het oppervlak van de sferoïde SI, zal gelijk zijn aan de cirkel waarvan de straal ML gegeven zal zijn, die namelijk in het kwadraat gelijk is aan het kwadraat van TK met tweemaal het kwadraat van SI 1).
Gegeven een gedeelte ABC van een parabool, waarvan de as is BK, de basis AC loodrecht op de as; en gevonden moet worden een rechte die gelijk is aan de kromme ABC.
Hieruit blijkt dus hoe de afmeting van een parabolische kromme afhangt van de kwadratuur van de hyperbool, en andersom de laatste van de eerste. {p. 78} En alle problemen die herleid worden tot een van deze twee, krijgen een getalsmatige oplossing die willekeurig dicht bij de ware ligt, met de bewonderenswaardige vondst van de logaritmen. Aangezien hiermee de kwadratuur van de hyperbool, zoals we eertijds hebben gevonden, met getallen zo dicht mogelijk wordt benaderd 3). Deze regel nu is als volgt. 1) Het is het speciale geval waarover gesproken wordt op p. 194-195 en 333-334 van T. XIV. 2) Zie p. 234-236 van T. XIV. 3) Zie p. 434-435 [Ned.] en 474 e.v. (1662) van T. XIV. |
[ 221 ] OVER AFWIKKELING VAN KROMME LIJNEN.
Neem het verschil van de logaritmen die overeenkomen met getallen die onderling dezelfde verhouding hebben als de rechten DE en BV; en van dit verschil wordt de logaritme gevraagd. Hieraan wordt toegevoegd deze logaritme (die altijd hetzelfde is) 0,36221,568871 1). De som zal zijn de logaritme van een getal dat de ruimte van DEVBAD zal aanduiden, door drie rechten en de kromme DAB omvat, in delen zoals waarvan parallelogram DC er 100000,00000 heeft. Waaruit verder ook gemakkelijk wordt verkregen de oppervlakte van het gedeelte DAB. {p. 79} Laat bijvoorbeeld de verhouding van DE tot BV zijn die van 36 tot 5. |
| Van | 1,55630,25008, | logaritme van 36. | ||
| wordt afgetrokken | 0,69897,00043. | logaritme van 5. | ||
| Dan is | 0,85733,24965. | het verschil van de logaritmen 2). | ||
| En | 9,93314,92856. | logaritme van het verschil. | ||
| Waarbij opgeteld | 0,36221,56887. | logarime die er altijd bij moet. | ||
| Geeft | 10,29536,49743. | logaritme van ruimte DEVBAD. |
|
Het getal van deze logaritme zal 11 cijfers hebben, daar de karakteristiek 10 is*). Laat dus eerst het dichtstbij kleinste getal worden gevraagd, overeenkomend met de gevonden logaritme, en dit getal is 19740. Dan worden uit het verschil van dezelfde logaritme, en de eerstvolgende in de tabel°), als overige cijfers gehaald 81026, te schrijven na de eerste, zodat er komt 197408,10260, met aan het eind een nul toegevoegd, om het karakteristieke getal 11 te maken. Dan is de oppervlakte van de ruimte DEVBAD zeer dicht bij 197408,10260 delen, zoals waarvan parallelogram DC er 100000,00000 heeft.
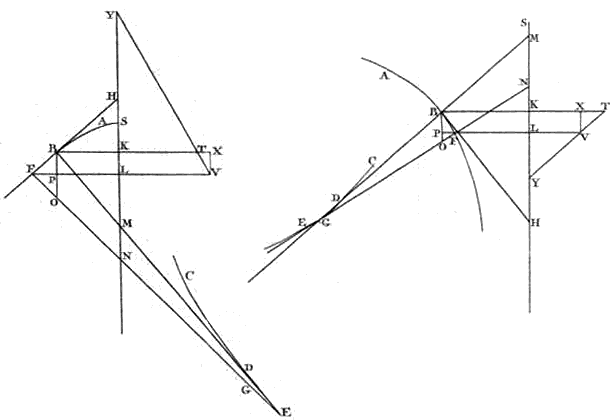
1) Zie over dit opmerkelijk exacte getal noot 2 van p. 476 van T. XIV. 2) In de oorspronkelijke uitgave had een drukfout, al verbeterd door 's Gravesande, het cijfer 2 veranderd in 1. Bij Huygens is elders het correcte getal te vinden: zie r. 5 van p. 477 van T. XIV, en p. 23 van Manuscript 13, waarover wordt gesproken in een noot op dezelfde p. 477. [ *) Zie bij Wikipedia, Logaritmetafel: de 'karakteristiek' heet nu de 'wijzer'.] [ °) Huygens kan gebruikt hebben: Adr. Vlacq, Arithmetica logarithmica, 1628.] KRommen te geven door afwikkeling waarvan ellipsen en hyperbolen worden beschreven, en rechten te vinden gelijk aan die krommen. 3) Gegeven een willekeurige ellips of hyperbool AB [Fig. 69], waarvan de dwarse as AC is, het middelpunt van de figuur D, het latus rectum ervan tweemaal AE. En genomen op de snede een of ander punt, zoals 3) Zie de noten 5-7 van p. 122 van T. XVII. |
[ 223 ] OVER AFWIKKELING VAN KROMME LIJNEN.
| B, wordt als ordinaat op de as gezet de rechte BK, en bij het genoemde punt B wordt de raaklijn getrokken die met de as samenkomt in F; en BG staat loodrecht op deze FB, en ontmoet de as in G; en BG wordt verlengd tot aan H, zodat BH tot HG de verhouding heeft die wordt samengesteld uit de verhoudingen van GF tot FK, en van AD tot DE. {p. 80} |
| [Fig. 69.] | ||
|
|
Ik zeg dat de kromme EHM, waarvan alle punten op dezelfde manier worden gevonden als punt H, de kromme is door afwikkeling waarvan, samen met de rechte EA, de kegelsnede AB zal worden beschreven. En dat BH de kromme raakt in H, en gelijk is aan de hele HEA. En daarom, als van HB wordt afgetrokken EA, dat de rest van de rechte gelijk zal zijn aan het gedeelte HE van de kromme. Nu blijkt, aangezien alle punten van de kromme, zonder onderscheid, op een bepaalde manier worden gevonden, dat deze in beide gevallen behoort tot die welke zuiver meetkundig worden genoemd. Waaruit volgt dat ook de relatie van al deze punten tot de punten van de as AC, door een of andere vergelijking zal kunnen worden uitgedrukt, en ik bevind dat deze vergelijking tot de zesde graad kan stijgen; en het kleinste aantal termen heeft, als AB een hyperbool is waarvan het latus transversum en het latus rectum gelijk zijn. Dan namelijk, als uit een willekeurig punt van de kromme, zoals H, de loodlijn HN is getrokken naar de as CAN; en AC wordt genoemd a; CN 1), x; en NH, y; zal altijd de derde macht van xx — yy — aa gelijk zijn aan 27 xxyyaa. Maar in dit geval kunnen punten van de kromme EHM ook veel sneller worden gevonden dan in de hier voorgeschreven constructie, zoals in het volgende zal worden aangetoond. Overigens is op te merken, dat bij een ellips de afzonderlijke kwadranten door afwikkeling van afzonderlijke lijnen worden beschreven; zoals het kwadrant ABL door afwikkeling van de lijn AEHM, kwadrant CL door afwikkeling van de gelijke ertegenover geplaatste COM. Er is namelijk in beide kegelsneden dit verschil dat, terwijl wel het begin van de kromme EHM zowel bij de ellips als bij de hyperbool het punt E is, met AE genomen gelijk aan ½ latus rectum, de genoemde lijn bij de hyperbool zich daarvandaan naar het oneindige uitstrekt, maar bij de ellips eindigt in het punt M van de kleine as, met LM genomen gelijk aan ½ latus rectum ten opzichte van ordinaten op de genoemde kleine as*). Want dat dit de 1) Lees: DN. [Zie T. XIV, p. 394, n.1 en Die Pendeluhr (1913), p. 96, met bewijs op p. 216.] [ *) Het eerste latus rectum (2 AE) is de koorde door een brandpunt loodrecht op de lange as, dat is b²/a, als a = halve lange as, b = halve korte as (zie Wolfram MathWorld, 'Semilatus Rectum'). Hier gaat het om a²/b, zie Die Pendeluhr.] |
[ 225 ] OVER AFWIKKELING VAN KROMME LIJNEN. {p. 81}
|
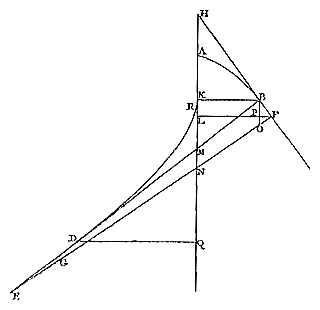
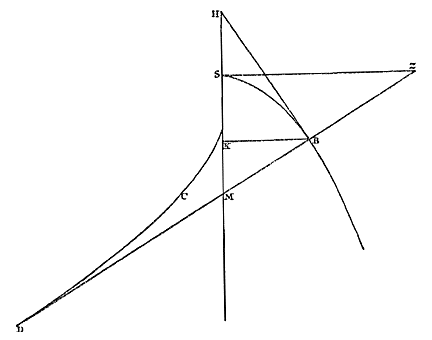
uiteinden zijn van deze kromme, blijkt gemakkelijk voor wie het ontstaan ervan onderzoekt, en wat bij een ellips geldt: zoals AD tot DE, zo is LM tot MD. Doch we zullen ons niet bezighouden met het bewijs hiervan, maar overgaan tot het behandelen van de methode zelf, waarmee zowel deze krommen uit kegelsneden, als talloze andere uit alle mogelijke andere krommen worden gevonden. GEgeven een kromme lijn, een andere te vinden door evolutie waarvan deze beschreven wordt; en aan te tonen dat uit elke meetkundige kromme een andere eveneens meetkundige kromme te voorschijn komt, waarbij een rechte lijn kan worden gegeven die eraan gelijk is. 1) Laat ABF een of andere kromme zijn [Fig. 70], of een deel ervan, naar één kant gebogen, en KL een rechte waarop alle punten betrekking hebben; en te vinden is een andere kromme, zoals DE, door afwikkeling waarvan die ABF wordt beschreven. Laat nu gesteld worden dat de kromme gevonden is; en aangezien het noodzakelijk is dat alle raaklijnen aan de kromme DE de lijn ABF, door afwikkeling beschreven, onder rechte hoeken ontmoeten, blijkt ook andersom dat de rechten die loodrecht staan op ABF, zoals BD en FE, de evoluut CDE zullen raken. {p. 82} We stellen ons twee punten voor, B en F, die zeer dicht bij elkaar liggen; en wanneer gesteld wordt dat de afwikkeling begint aan de kant van A, en F daar verder vandaan ligt dan B, zal ook het contactpunt E verder dan D van A liggen; en het snijpunt van de rechten BD en FE, dat G is, zal op de rechte BD voorbij punt D vallen. Want het is noodzakelijk dat die BD en FE samenkomen, daar ze loodrecht op de holle kant van de kromme staan. 1) Vergelijk p. 206 en 387 (noot 2) van T. XIV, en ook § 1 op p. 142 en § 5 op p. 146 van T. XVII, met name noot 3 van p. 143 van dit laatste deel, waar de eerste Fig. 70 staat. Daar is opgemerkt dat de letter C van § 1 ontbreekt in deze figuur; Huygens heeft echter in zijn exemplaar van Hor. osc. deze letter met de hand toegevoegd, zodat de overeenkomst met de tekst van § 1 sindsdien compleet is. |
[ 227 ] OVER AFWIKKELING VAN KROMME LIJNEN.
|
En hoe dichter punt F bij B ligt, des te dichter blijken ook de punten D, G en E bij elkaar te komen; en daarom, als wordt aangenomen dat de tussenruimte BF oneindig smal is, zullen de drie genoemde punten voor één en hetzelfde gehouden moeten worden; en nog bovendien, als de rechte BH is getrokken die de kromme in B raakt, zal deze ook gezien kunnen worden als de raaklijn in F. Neem BO evenwijdig met KL, en laat hierop loodrecht vallen BK en FL; en FL snijdt de rechte BO in P, en de punten M en N zijn de punten waarin de rechten BD en FE die KL ontmoeten. Omdat dan de verhouding van BG tot GM dezelfde is als die van BO tot MN, zal als de laatste verhouding gegeven is ook de eerste bekend zijn; en omdat de rechte BM gegeven wordt in grootte en ook ligging, zal ook punt G op het verlengde van BM gegeven worden, oftewel D op de kromme CDE, omdat we hebben gezegd dat G en D samenvallen 1). Nu is de verhouding van BO tot MN wel eenvoudig te geven bij de cycloïde, waar we deze als eerste van allen hebben opgespoord, en gevonden als het dubbele 2); maar bij andere krommen, die we tot dusver hebben onderzocht, met een samenstelling van twee gegeven verhoudingen. Want omdat de verhouding van BO tot MN wordt samengesteld uit de verhoudingen van BO tot BP, of van NH tot LH, en uit die van BP of KL tot MN, blijkt dat, als deze beide verhoudingen gegeven worden, ook de daaruit samengestelde verhouding van BO tot MN gegeven gaat worden. En dat die eerste bij alle meetkundige krommen gegeven worden, zal in het volgende blijken; en zo dus dat daaraan altijd krommen kunnen worden toegewezen, door afwikkeling waarvan ze beschreven worden, en die daarom tot rechte lijnen zijn te herleiden. 1) Deze berekening in moderne notatie — zie hierover p. 44 van het Voorbericht — is te vinden op p. 143 van T. III van de Vorlesungen über Geschichte der Mathematik van M. Cantor (2e ed. Leipzig, 1901) en noot 70 van de Duitse vertaling van Hor. osc. door A. Hekscher en A. v. Oettingen, 1913. [Die Pendeluhr, p. 218.] [...] Jacob Bernoulli vond later voor de kromtestraal BG de uitdrukking ds3/dx ddy ('Curvatura laminae elasticae...', in Acta Eruditorum, 1694, p. 264). [In Opera (1744) 4, p. 576 (fig.). Zie: Ralph Levien, 'The elastica: a mathematical history', 2008.] 2) Zie § 3 op p. 145 van T. XVII; en ook noot 2 op p. 142 daarvoor, en noot 1 op p. 404 van T. XIV. |
[ 229 ] OVER AFWIKKELING VAN KROMME LIJNEN.
|
Laat eerst gesteld worden dat ABF [Fig. 71] een parabool is, met top A en as AQ. Aangezien dan de lijnen BM en FN onder rechte hoeken op de parabool staan, en BK en FL loodrecht op de as AQ getrokken zijn; zullen, volgens een eigenschap van de parabool, MK en NL elk gelijk zijn aan de helft van het latus rectum; en met de gemeenschappelijke LM er afgenomen, zullen KL en MN aan elkaar gelijk zijn. Hieruit, aangezien de verhouding van BG tot GM wordt samengesteld uit de verhoudingen van NH tot HL, en KL tot MN (zoals gezegd), en de laatste ervan de gelijkheidsverhouding is, is duidelijk dat de verhouding van BG tot GM dezelfde zal zijn als die van NH tot HL; en door te verdelen, die van BM tot MG dezelfde als die van NL tot LH, of van MK tot KH; want LH en KH zijn voor dezelfde te houden, wegens de nabijheid van de punten B en F. |
|
Gegeven is nu de verhouding van MK tot KH, bij gegeven punt B; aangezien zowel MK als KH in grootte gegeven worden; want MK is gelijk aan de helft van het latus rectum, en KH het dubbele van KA. Ook is gegeven in positie en grootte de rechte BM. Dus ook MG zal gegeven zijn, en daarom ook punt G, oftewel D, op de kromme RDE; dat punt wordt namelijk gevonden door BM te verlengen tot in G, zodat BM tot MG is zoals ½ latus rectum tot tweemaal KA. {p. 83}
En zo zijn wel, als op de parabool ABF behalve B willekeurig veel punten worden genomen, ook evenzoveel punten van de lijn RDE op dezelfde manier te vinden; en hierdoor staat vast dat RDE een meetkundige lijn is, en tegelijk wordt een eigenschap ervan bekend, waaruit andere kunnen worden afgeleid. 1) Lees RDE [Fig. 71]. [ *) Het gelijkteken '=' staat hier in plaats van het door Huygens gebruikte |
[ 231 ] OVER AFWIKKELING VAN KROMME LIJNEN.
|
en dat deze kromme daarom de parabolische kromme is, door evolutie waarvan de parabool AB wordt beschreven, zoals we boven hebben aangetoond [Prop. 8]; van deze parabolische kromme is namelijk het latus rectum gelijk aan 27/16 maal het latus rectum van parabool AB. Dan wordt immers het latus rectum van deze laatste gelijk aan 16/27 maal het latus rectum van de parabolische kromme, zoals daar is bepaald. Verder is nu duidelijk hoe de verhouding van OB tot BP, of van NH tot HL, altijd kan worden gevonden, niet alleen wanneer ABF een parabool is, maar ook ieder mogelijke andere meetkundige kromme. Aangezien alleen de rechte FH moet worden getrokken, die de kromme in het aangenomen punt F raakt [Fig. 70], en FN loodrecht op deze FH; waardoor NH en HL gegeven zullen zijn, en zo wordt dus ook hun verhouding gegeven. {p. 84} Maar het is niet even duidelijk hoe de verhouding van KL tot MN bekend wordt, die evenwel ook altijd kan worden gevonden, zoals we als volgt aantonen. Neem de rechten KT en LV loodrecht op KL, met KT gelijk aan KM, en LV gelijk aan LN, en trek VX evenwijdig met LN, die KT ontmoet in X. Aangezien dan altijd het verschil tussen LK en NM hetzelfde is als dat van LN en KM, dat is als van LV en KT — en het verschil tussen LV en KT is gelijk aan XT, en XV aan LK — zal derhalve NM gelijk zijn aan de twee samen VX en XT, of aan het overschot van VX boven XT. En zo, als gegeven is de verhouding van VX tot XT, zal ook gegeven zijn de verhouding van VX tot beide samen VX en XT, of tot het overschot van VX boven XT, dat is, gegeven zal zijn de verhouding van VX of LK tot NM. |

|
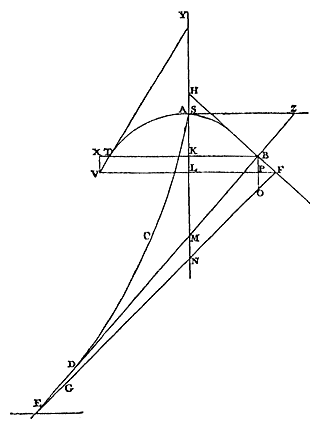
Nu is te weten, aangezien KT aan KM, en LV aan LN gelijk genomen zijn, dat de meetkundige plaats van de punten T en V zal zijn een bepaalde gegeven rechte of kromme lijn, zoals dadelijk wordt aangetoond. En wanneer het een rechte lijn is, zoals het geval is als ABF een kegelsnede is, en KL de as ervan, dan staat vast dat de verhouding van VX tot XT gegeven is, bij gegeven positie van de lijn VT, die de plaats is van de punten V en T; en dat dan altijd dezelfde genoemde verhouding verkregen wordt, hoe het interval KL ook is. {p. 85} Maar als de plaats een andere, kromme lijn is, zal de verhouding van VX tot XT verschillend zijn, naar gelang het interval KL groter of kleiner is. Nu is te onderzoeken welke deze verhouding zal zijn, wanneer we ons KL oneindig klein voorstellen, aangezien we ook hebben gesteld dat de punten B en F zeer dicht bij elkaar liggen. Evenzo moet dus worden aangenomen dat ook de punten V en T een zeer klein stukje van de kromme lijn onderscheppen; waaruit volgt dat de rechte VT zal samenvallen met die welke de kromme in T raakt. Laat die raaklijn dan TY zijn; ze kan immers getrokken worden aangezien de kromme waarop de punten T en V liggen, een meetkundige kromme is 1). Dan zal de verhouding van YK tot KT gegeven zijn, en zo ook die van VX tot XT, waaruit ook de verhouding van LK tot NM gegeven wordt, zoals we hebben aangetoond. En welke lijn het nu is waarop depunten T en V liggen, wordt gevonden door een zeker punt S op de rechte KL te stellen, en noem SK, x; KT, y. Want omdat gegeven is de kromme ABF, en omdat BM daarop onder rechte hoeken is getrokken, is daaruit te vinden de grootte van lijn KM, met de methode van raaklijnen door Descartes geleverd 2), die gelijk is aan KT of y, en uit deze gelijkheid wordt de aard van de kromme TV bekend, waaraan dan de raaklijn is te trekken. Maar alles zal helderder worden met het volgende voorbeeld. Laat ABF [Fig. 72] die parabolische kromme zijn, waarbij we hierboven een rechte hebben gevonden die eraan gelijk is [Prop. 9]; daarbij verhouden zich namelijk de derde machten van lijnen loodrecht op de rechte SK, tot elkaar als de kwadraten van de abscissen op deze SK. En gevonden moet worden de kromme CDE door afwikkeling waarvan de parabolische kromme SBF wordt beschreven. Hier is ten eerste de verhouding van BO tot BP makkelijk te vinden, omdat we weten dat in punt B de raaklijn aan de parabolische kromme wordt getrokken, als SH gelijk aan ½ SK genomen wordt. Bij deze raaklijn, waar BM loodrecht op staat, worden nu de lijnen MH en HK gegeven, en dus ook hun onderlinge verhouding, die dezelfde is als die van OB tot BP. 1) Zie over de constructie van raaklijnen aan meetkundige krommen p. 442-448 van T. XIV, met name noot 6 van p. 446 over het algoritme van Hudde [Extrait d'une lettre de feu M. Hudde, Journ. Lit. 1703], en noot 3 van p. 442, waar verwezen wordt naar p. 315 van T. IV: de 'Regula' in de brief van Huygens aan J. de Witt van 25 feb. 1663. 2) In het tweede boek van de 'Géométrie' (ed. Adam & Tannery, T. VI, p. 413-424); zie p. 17 van T. XI en noot 10 van p. 65 van T. XII. |
[ 235 ] OVER AFWIKKELING VAN KROMME LIJNEN.
|
Opdat nu de verhouding van BP, of KL tot MN bekend wordt, worden loodrecht op KL de rechten KT en LV gezet, afzonderlijk gelijk aan KM en LN, en VX is evenwijdig aan LK. Nu, als van de twee samen KL en LN wordt afgetrokken KM, blijft over MN 1); dat is, als van de twee XV en VL, of XV en XK, wordt afgetrokken KT, blijkt over te blijven VX en XT; daarom zullen deze twee VX en XT gelijk zijn aan MN, en zo is dus de verhouding van KL tot MN dezelfde als die van VX tot de twee samen VX en XT. Opdat nu deze verhouding bekend wordt wanneer het interval KL heel klein is, moet men volgens wat boven gezegd is onderzoeken welke plaats of lijn het is waarop de punten T en V liggen. Neem daartoe het latus rectum van de parabolische kromme ABF = a; SK = x; KT = y. {p. 86}
Omdat dus evenredig zijn KH, KB, KM, en HK = 3/2 x; en KB volgens de aard van de parabolische kromme gelijk is aan 3√axx; komt er KM, dat is KT = 2/3 3√axx = y, en zo dus 8/27 aax = y3. Waaruit blijkt dat de plaats van de punten T en V zo'n parabolische kromme is, die meetkundigen een kubische [^] noemen. Daaraan moet derhalve in T de raaklijn worden getrokken, met SY als dubbele van SK, en Y met T verbonden. De kortste constructie bereiken we hier op de deze manier. KT of KM was y genoemd. Dus MH zal zijn y + 3/2 x. En MH is tot HK, of OB tot BP, zoals y + 3/2 x tot 3/2 x, of als van alles het dubbele wordt genomen, zoals 2 y + 3 x tot 3 x. Omdat verder YK = 3 x, zal YK tot YK + KT, of volgens wat eerder gezegd is, KL tot MN zijn, zoals 3 x tot 3 x + y. Maar nu hebben we gezegd dat uit de verhoudingen OB tot BP, en KL tot MN, wordt samengesteld de verhouding van BD tot DM. Dus de verhouding van BD tot DM zal zijn samengesteld uit de verhoudingen 2 y + 3 x tot 3 x, en 3 x tot 3 x + y; en daarom zal die zijn van 2 y + 3 x tot 3 x + y. En door verdelen: de verhouding van MB tot MD zal dezelfde zijn als van y tot 3 x + y. {p. 87}
Neem SZ loodrecht op SK, en de verlengde MB ontmoet deze in Z. Omdat dus de verhouding van BM tot MD gevonden is als van y tot y + 3 x, dat is die van MK tot MK + 3 KS; en zoals MK tot MK + 3 KS is, zo is MB tot MB + 3 BZ; daarom zal MB tot MD zijn zoals MB tot MB + 3 BZ. Waaruit blijkt dat MD gelijk genomen moet worden aan MB + 3 BZ. En op een dergelijke manier, als we het onderzoeken bij die parabolische kromme, of bij een kubische parabool [Fig. 73], waarbij de derde machten van ordinaten zich tot elkaar verhouden zoals de van de as afgesneden gedeelten, 1) Huygens schreef erbij: "Hier wordt verondersteld dat de rechte LN groter is dan KM, wat beter eerst had kunnen worden bewezen, ook al is het waar". 's Gravesande geeft dit bewijs in zijn uitgave van 1724. Het is gemakkelijk te verifiëren dat bij de beschouwde kromme de subnormaal des te groter is naarmate het beschouwde punt van de kromme dichter bij de top ligt. |
[ 237 ] OVER AFWIKKELING VAN KROMME LIJNEN.
zullen we vinden dat de kromme door evolutie waarvan ze wordt beschreven, en die derhalve gelijk gesteld kan worden aan een rechte lijn, met een niet moeilijkere constructie door punten te bepalen is.
Nu zijn er hier, wat opmerkenswaard is, en wat ook bij enige andere van deze parabolische krommen het geval is, twee afwikkelingen in tegengestelde richtingen, die beide beginnen vanaf een zeker punt A; zodanig dat door afwikkeling van ARD, verder voortgezet naar het oneindige, wordt beschreven het oneindige deel ABF van de parabolische kromme; en door afwikkeling van de hele ARI, eveneens uitgestrekt naar het oneindige, slechts het stukje AS. En het punt A woordt bepaald als genomen is SP die zich tot het latus rectum van de parabolische kromme verhoudt, als de eenheid tot de vierdemachtswortel uit het getal 91125 (dit is de derde macht van 45), en de ordinaat PA. Waaruit verder het punt R, grenspunt van de twee krommen RD en RI, wordt gevonden zoals alle overige van deze krommen, dat is, zoals het punt D zojuist gevonden is. {p. 88} Tenslotte, welke soort van parabolische kromme de kromme SAB ook is, we hebben bevonden dat altijd even gemakkelijk een andere kromme met punten is te vinden, door afwikkeling waarvan ze beschreven wordt, en die daarom aan een rechte gelijkgesteld kan worden. En zo tonen we de algemene constructie in het volgende tabelletje, dat uitgebreid kan worden zo ver als men wil. |
| Als | 
| ax = y2 | zal gelden |  | BM + 2 BZ |  | = BD. |
| a2x = y3 | 1/2 BM + 3/2 BZ | ||||||
| ax2 = y3 | 2 BM + 3 BZ | ||||||
| ax3 = y4 | 3 BM + 4 BZ | ||||||
| a3x = y4 | 1/3 BM + 4/3 BZ |
| Laat SB [Fig. 74] een parabool zijn, of een of andere parabolische kromme, waarvan de top S is, de rechte SK ofwel de as, of een loodlijn op de as, waarop de punten van de parabolische kromme betrekking hebben in een vergelijking; en verondersteld wordt dat deze SK altijd naar de holle kant is getrokken; waarop SZ loodrecht staat. |
| Door nu te stellen SK = x; BK = y, die van een willekeurig punt van de kromme loodrecht staat op die SK; en het latus rectum van de kromme = a verklaart het eerste deel van het tabelletje, dat links staat, de aard |
[ 239 ] OVER AFWIKKELING VAN KROMME LIJNEN. {p. 89}
|
van afzonderlijke parabolische krommen met afzonderlijke vergelijkingen. Waarmee in het rechterdeel overeenkomen de grootten van de lijn BD die, als ze loodrecht op de kromme SB staat, het punt D op de gezochte kromme CD zal geven. Bijvoorbeeld, als SB een parabool is die ontstaat uit een kegelsnede, weten we dat daarmee overeenkomt de eerste vergelijking van de tabel, ax = y2; waarmee aan de andere kant correspondeert BM + 2 BZ = BD. Waaruit de lengte van de lijn BD bekend wordt, en zo het vinden van willekeurig veel punten van de kromme CD. En dat deze in dit geval althans een parabolische kromme is, werd hierboven bewezen, het is namelijk die waarvan de vergelijking de derde van deze tabel is. Nu wordt het tabelletje samengesteld op deze manier, dat van BM wordt genomen een veelvoud volgens het getal dat in de vergelijking de exponent is van de macht van x; en van BZ het veelvoud volgens de exponent van de macht van y; nu moet van wat met deze beide wordt samengesteld, het deel genomen worden dat genoemd staat als exponent van de macht van a 1).
|
|
Om nu de aard van de overige uit te leggen: PS en SK zijn asymptoten van de kromme AB, die een rechte hoek omvatten, en vanaf een willekeurig punt B van de kromme wordt getrokken
1) Inderdaad vindt, men met als vergelijking van de 'paraboloïde' of parabool van hogere graad ya = kxb, waarin k een rechte is tot de macht a – b (zoals de notatie in vorige delen was, zie noot 2 van p. 147 van T. XVII): BD = (b.BM + a.BZ) / (a – b). |
[ 241 ] AFWIKKELING VAN KROMMEN.
|
BK evenwijdig met PS, en SK = x; KB = y. Als AB dus een hyperbool is, weten we dat de rechthoek van de lijnen SK en KB, dat is, de rechthoek xy altijd gelijk is aan hetzelfde vierkant, dat genoemd wordt aa. {p. 90} En de eerstvolgende zal zijn een hyperbolische kromme, waarbij het lichaam uit het vierkant van de lijn SK, naar de hoogte KB opgetrokken, dat is het lichaam xxy, gelijk is aan een bepaalde kubus, die genoemd wordt a3. En zo komen er talloze andere hyperbolische krommen van deze soort, waarvan het volgende tabelletje de eigenschap toont met de afzonderlijke vergelijkingen, en tegelijk de manier om de kromme DC te construeren, door afwikkeling waarvan elke wordt voortgebracht. |
| Als | 
| xy = a2 | zal gelden |  | 1/2 BM + 1/2 BZ | 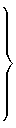 | = BD. |
| x2y = a3 | 2/3 BM + 1/3 BZ | ||||||
| xy2 = a3 | 1/3 BM + 2/3 BZ | ||||||
| x3y = a4 | 3/4 BM + 1/4 BZ | ||||||
| xy3 = a4 | 1/4 BM + 3/4 BZ |
|
De rechte DBMZ snijdt de kromme, zoals eerder ook, onder rechte hoeken, en ontmoet de asymptoten SK en SP in M en Z. Als dus bijvoorbeeld de hyperbool is AB, waarvan de vergelijking is xy = a2, moet worden genomen BD = 1/2 BM + 1/2 BZ, zoals het tabelletje voorschrijft. En het punt D zal het gevraagde punt op de kromme DC zijn, waarvan willekeurig veel andere punten zo kunnen worden gevonden, en een willekeurig gedeelte ervan is gelijk te stellen aan een rechte lijn. En dit is juist die zelfde kromme, waarvan we de relatie met de as van de hyperbool hierboven [p. 223] in een vergelijking hebben uitgedrukt. De constructie nu van dit tabelletje is geheel hetzelfde als hierboven 1).
Overigens, aangezien voor de constructie van zowel deze krommen, als van die welke uit parabolische krommen ontstaan, getrokken moeten worden lijnen DBZ, die in een gegeven punt B de krommen AB, of hun raaklijnen BH, onder rechte hoeken snijden, zullen we in het algemeen zeggen hoe deze raaklijnen te vinden zijn. In de vergelijking dus, die de aard van elke kromme verklaart — en zulke vergelijkingen worden uiteengezet in de twee voorgaande tabelletjes — moet bekeken worden wat de exponenten zijn van de machten van x en y, en het moet zo gemaakt worden dat geldt: zoals de exponent van de macht van x tot de exponent van de macht van y, zo SK tot KH 2). De verbindingslijn HB zal namelijk de kromme in B raken. 1) Met de vergelijking van de hyperbool van hogere graad xbya = k, waarin k een rechte is tot de macht a + b, vindt men inderdaad BD = (b.BM + a.BZ) / (a + b). 2) Vergelijk noot 1 van p. 233 hiervoor. Volgens de daar genoemde 'Regula' wordt de subtangens van de kromme xbya – k = 0 (KH in Fig. 74) gelijk aan a/b x (waarin x de rechte SK is). Dus SK : KH = b : a. 3) Zie p. 197-198 en 288-293 (daterend van 1657) van T. XIV.
|