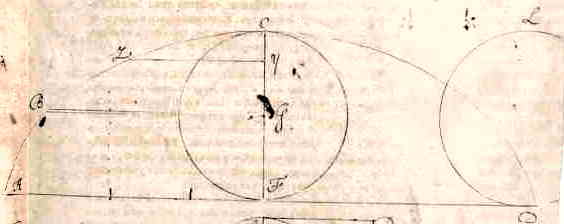
No 494. Problemen van Bl. Pascal. juni 1658.   Aanhangsel bij No. 493 Het stuk is gepubliceerd in de Oeuvres Complètes de Bl. Pascal, Tome III, Paris, 1866. in-8o.*) Problemen over de Cycloïde, voorgesteld in de maand juni 1658.     De definitie van de cycloïde is te vinden aan het eind van dit geschrift.     Toen wij enige maanden geleden studeerden op bepaalde dingen omtrent de cycloïde, en de zwaartepunten ervan, kwamen we tot vraagstukken die vrij diepgaand en moeilijk zijn, naar ons leek; en daarvan verzoeken we deemoedig de oplossing van de voortreffelijkste meetkundigen van de gehele wereld, en hun wordt een prijs in het vooruitzicht gesteld, niet om het geld (dat zou verre van ons zijn!) maar tot openlijk bewijs van onze gedienstigheid, of liever van de verdienste van hen die deze zullen vinden.     Wat we dan voorstellen is van deze aard. Gegeven is een willekeurig punt Z op welke cycloïde dan ook, ABCD, van waaruit getrokken wordt ZY evenwijdig met de basis AD, die de as CF snijdt in het punt Y. Gevraagd worden:   [ *)  1865, p. 322.  Orig.: 1658.]

[ 188 ]

De grootte van het oppervlak CZY; en het zwaartepunt ervan; de vaste lichamen ontstaan door omwenteling van het genoemde oppervlak CZY, zowel om ZY als om CY; en de zwaartepunten van deze lichamen.     En als deze zelfde lichamen gesneden worden met een vlak, getrokken door de as, en er zo in beide gevallen twee lichamen komen — namelijk twee uit het lichaam rondom de basis ZY, en twee uit het lichaam rondom de as CY ontstaan — vragen we van elk van deze lichamen ook de zwaartepunten.     Omdat echter het bewijs van de gevraagde dingen wellicht zo lang zal worden, dat het nauwelijks binnen de gestelde tijd behoorlijk genoeg behandeld kan worden, en het vernuft en de vrije tijd van de geleerdste meetkundigen in overweging nemend, verlangen we van hen slechts dat ze aantonen, hetzij op de wijze der Ouden, hetzij dan toch met de theorie der indivisibilia (deze bewijsmethode gebruiken wij namelijk het liefst), dat al het gevraagde gegeven wordt; zodat gemakkelijk uit het bewezene willekeurige gevraagde punten kunnen worden gevonden uit dingen die bij hypothese gegevens zijn.     En om mij duidelijker te verklaren, en niets dubbelzinnigs over te laten, licht ik de zaak met een voorbeeld toe. Laat het geval voorgelegd worden van een parabool ABC, met as AB, basis AC, raaklijn BD, loodrecht op de as AB. Gevonden moet worden het zwaartepunt van het vlakdeel DCB. Ik zal oordelen dat aan het probleem voldaan is als wordt bewezen, dat het zwaartepunt van parabool ABC gegeven is, en ook het zwaartepunt van rechthoek CDBA, en de verhouding van deze rechthoek met de parabool CBA; en dat daarom gegeven is het zwaartepunt van het gevraagde vlakdeel CDB. Want ook al wordt niet precies het punt geleverd waarin het zwaartepunt verkregen wordt, toch is bewezen dat het een gegeven is, omdat datgene waaruit het gevonden wordt gegeven is; en het zal erop neerkomen, dat er niets anders overblijft dan een berekening, waarbij noch de kracht van het verstand noch de ervaring van een meester vereist is; en daarom wordt die berekening niet door ons verlangd, waarom zouden we ons immers daarin verdiepen? Maar we vragen alleen maar dat bewezen wordt dat de dingen die voorgelegd worden gegeven zijn.     Maar de geleerdste meetkundigen zullen van mening zijn dat het volgende volstrekt noodzakelijk is, en we verlangen het van hen: van twee voorstellen, dan wel van twee gevallen, een gehele constructie of een gehele berekening.     Het eerste geval is wanneer punt Z gelegd wordt in A.     Het tweede, wanneer hetzelfde punt Z gegeven wordt in B, waardoor de parallel GB loopt, getrokken vanaf het punt G, middelpunt van de cirkel die de cycloïde voortbrengt.     Maar als bij deze twee gevallen een of andere rekenfout binnengeslopen is, vergeven we hem met genoegen, en een gunst die wij zelf zouden vragen kunnen zij makkelijk krijgen.

[ 189 ]

Wie het boven voorgelegde voor de eerste dag van de maand oktober van het jaar 1658 opgelost en bewezen heeft, is voor ons de grote Apollo.*)     En de eerste zal dan de waarde van veertig Spaanse gouden dubloenen krijgen, die de Spanjaarden zelf doblones noemen, en de Fransen pistoles; of in elk geval, als hij het liever wil, de goudstukken zelf.     De tweede echter twintig van die gouden dubloenen. Als slechts één persoon het opgelost heeft, krijgt hij alleen er zestig.     En omdat we de zaak serieus behandelen, hebben we ervoor gezorgd dat de genoemde zestig gouden dubloenen in bewaring gegeven werden bij de illustere heer de Carcavi, koninklijk raadgever te Parijs, verblijvend bij de zeer voorname heer de hertog van Liancourt; die ze zal uitbetalen zodra de bewijzen die naar hem gezonden worden als waar en meetkundig beoordeeld worden, door personen die door hem daartoe gemachtigd zijn. En daar we de illustere raadgever al vele jaren kennen als een rechtschapen man, en als iemand die de wiskunde zeer liefheeft, durven we beloven dat de zaak eerlijk en zonder bedrog ten uitvoer gebracht zal worden.     Maar als ongeveer deze drie maanden verlopen zijn en niemand gevonden wordt die het door ons gevraagde heeft opgelost, zullen we niet verloochenen wat we zelf gevonden hebben, en we zullen het anderen niet misgunnen om daaruit belangrijker dingen te verkrijgen dan wat al gevonden is, en daarmee oogsten we wellicht dankbaarheid bij het nageslacht.     Dit ene blijft over, dat we een beschrijving geven van de cycloïde-lijn, waarvan we meenden kortheidshalve af te kunnen zien, daar deze lijn al lang geleden aan Galileï, Torricelli, en anderen bekend is geworden; maar omdat hun boeken niet voor allen beschikbaar zijn, daarom geven we de volgende van Torricelli.°)   [ *)  Vergilius, Eclogae vel bucolica III, 104.]   [ °)  Evangelista Torricelli, Opera geometrica (1644), App. ]

Beschrijving van de cycloïde.

Neem op een liggende rechte DA, een cirkel DL die de rechte DA raakt in het punt D, en teken punt D aan als een vast punt op de omtrek van cirkel DL. Stel u dan voor dat bovenop de liggende lijn DA de cirkel DL gedraaid wordt, met een beweging die cirkelvormig is en tegelijk voortgaat naar de kant van A, zodanig dat hij altijd onmiddellijk met één punt de rechte lijn DA raakt, totdat het vaste punt D weer contact maakt, neem aan in A. Het is zeker dat het vaste punt D op de omtrek van de rollende cirkel DL een of andere lijn beschrijft, die eerst oprijst vanaf de onderliggende lijn DA, vervolgens zijn top bereikt bij C, en tenslotte steil aflopend neerkomt bij punt A; en zo'n lijn heet een cycloïde.

No 500. [ Bl. Pascal ] Bijvoegsel. [juli 1658.]   Aanhangsel bij No. 499 Het stuk is gepubliceerd in de Oeuvres Complètes van Bl. Pascal, T. III, Paris, 1866. in-8o.  [1658.] Bijvoegsel bij de problemen over de Cycloïde.     Daar de heer de Carcavi ons heeft aangewezen dat er bij wat we over de cycloïde voorstelden twee plaatsen dubbelzinnig zijn, hebben we terstond gemeend dat hieraan tegemoetgekomen moest worden, en als volgt komen we eraan tegemoet.     De eerste komt daarvandaan, dat we bij het voorstellen van onze problemen over de cycloïde deze woorden

[ 197 ]

gebruikt hebben: "op welke cycloïde dan ook", terwijl we toch slechts van één soort cycloïde een definitie hebben aangevoerd. Maar we bedoelen niets anders dan alleen die eenvoudige, natuurlijke en voornaamste cycloïde, waarvan we uit Torricelli een beschrijving gegeven hebben; aangezien namelijk wat daarover ontward wordt gemakkelijk is over te brengen op alle andere soorten, zal iemand die alleen bij deze onze problemen opgelost heeft, geheel aan onze eisen voldaan hebben.     De laatste bestaat daar in, dat door ons niet precies is gesteld of we veronderstellen dat gegeven is de verhouding van de basis AD van de cycloïde met de hoogte ervan, oftewel met de middellijn FC van de voortbrengende cirkel; maar we meenden dat het als toegestaan aan te nemen was dat de verhouding zelf is gegeven, en we veronderstellen dat deze gegeven is, zoals geheel en al billijk is.     Nu is er dus geen onduidelijkheid meer. Eén ding lijkt er toch nog te zijn, om de geleerdste meetkundigen uit te nodigen onze problemen met minder moeilijkheden en meer genoegen te onderzoeken; namelijk al dat weg te nemen wat niet past bij de scherpzinnigheid van het verstand, die we bij uitstek hoog achten, en voorgenomen hebben te verkennen en te bekronen; zoals de gehele berekening van veel gevallen die we verlangden, en ook een volledige beschrijving van de oplossingen; daar deze niet afhangen van de kracht van het verstand, maar van andere omstandigheden. Slechts het volgende hebben we nu dus opgesteld, opdat alleen te overwinnen blijft de moeilijkheid van de problemen. Namelijk:     Wie met een document, binnen de vooraf vastgestelde tijd, aan de illustere heer de Carcavi te kennen heeft gegeven dat hij het bewijs in handen heeft van dat wat gevraagd is; en hetzij datzelfde bewijs, hoe beknopt ook, naar hem gezonden heeft; hetzij, als hij nog niet de tijd gehad heeft het op papier te zetten, althans ter bevestiging van de waarheid van zijn bewering de berekening gegeven heeft van het geval dat we hierna zullen aanduiden, en zich bereid heeft verklaard alles geheel te bewijzen op verzoek van dezelfde heer de Carcavi; deze persoon, verklaren we, heeft aan onze eisen voldaan; en we stemmen ermee in dat de eerste die dit gedaan zal hebben met de eerste, en de tweede met de tweede prijs begiftigd moet worden, als zijn oplossing door de heer de Carcavi zelf, en na vertoning aan personen daartoe bij hem genodigd, zoals hem het beste lijkt, meetkundig en waar geoordeeld zal worden, steeds behoudens rekenfouten.     En het ene geval waarvan de berekening zal volstaan is het volgende. Als de halve cycloïde ACF om de basis AF gedraaid wordt, en het vaste lichaam daaruit ontstaan wordt doorsneden met een vlak door dezelfde AF (die nu de as van dit lichaam is), dat natuurlijk het lichaam in twee gelijke helften verdeelt, verlangen we dat van één van deze beide halve lichamen het zwaartepunt aangegeven wordt.   [ B. Pascal, Historia Trochoidis (1658) en Histoire de la Roulette (1658), Récit de l'examen et du jugement des escrits envoyez pour les prix (1658), Historiae trochoidis, sive cycloïdis continuatio en Suite de l'histoire de la roulette.  Zie ook T.XXII, p. 517.]