|
No 483.
Christiaan Huygens aan [J. Wallis].april 1658 (Concept). 1) |
| 1658 Aprili.
|
| a) |
|
| b) |
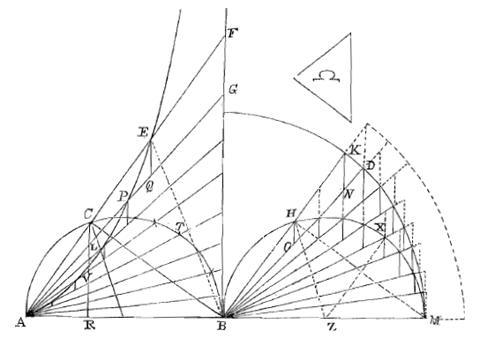
| APE is een Cissoïde*) van Diocles, ACB de cirkel waaruit hij is ontstaan; Altijd is dan AC = EF. Ik zeg dat het oppervlak AVPEFB gelijk is aan driemaal het segment CBT + driehoek ACB. |
|
∠ MBH = BAC. BM = AB. Driemaal segment CBT + driehoek ACB = sector BKM + oppervlak HXMK, want segment CBT of HMX = oppervlak HXMK.
1) Dit stuk is hier gezet onder de datum van 'Adversaria'. Toch is het pas later aan Wallis gestuurd. Op de plaats van noot 6 hierna [Wallis, Mechanica, 1695, vol. 1, p. 906] is te lezen: Op deze meting van een Cissoïdaal oppervlak heeft mij als eerste opmerkzaam gemaakt (maar zonder bewijs) de weledele heer Christiaan Huygens (een man met een scherp en vlug verstand), in een brief aan mij van 6 augustus 1658 [waarschijnlijk brief No. 512 van 6 september].
Een brief van Wallis van 1 jan. 1659 [>] geeft aan dat hij deze brief had ontvangen; maar uit een brief van Chr. Huygens van 31 jan. 1659 [No. 574, n.1, p. 329 hierna] blijkt dat deze het bewijs al aan Wallis had gestuurd.
a) Er moet een propositie aan voorafgaan, dat bij de sector BKM kan worden ingeschreven en omgeschreven een getande figuur zó, dat de ene de andere overtreft met een kleiner dan willekeurig gegeven oppervlak. [Chr. Huygens]. |
[ 171 ]
|
∠ HZM = 2 ∠ HBM, dus sector ZHM = ½ sector BKM, dus sector ZHM = Δ BHZ + opp. HXKM. Als gelijke worden weggenomen, aan de rechterkant Δ BHZ, aan de linkerkant Δ ZHM, komt er: opp. HXMK = segment HMX. Aangetoond moet dus worden dat oppervlak AVPEFB = sector BKM + oppervlak HXMK. Als gezegd wordt dat het oppervlak van de cissoïde kleiner is dan deze: laat het overschot ervan zijn Ω. En laat bij sector BKM een figuur ordinaatsgewijs worden ingeschreven, zodat het dubbele van alle tandjes KND kleiner is dan Ω. En bij het oppervlak van de Cissoïde wordt een figuur ingeschreven bestaande uit evenveel trapezia. |
| Aangetoond zal worden dat trapezium EFGQ = Δ BKN + trapezium HN. Immers trapezium EG staat tot Δ ACL als FG + EQ tot CL (omdat ze dezelfde hoogte hebben), dat is als FA + AE tot AC, dat is als AF + FC tot AC, dat is als AB + BR tot RA. |
| Dus door samenstellen: trapezium EG + Δ ACL staat tot Δ ACL als 2 AB tot AR, dat is als 2 × vierkant AB tot vierkant AC, of als 2 × vierkant BK tot vierkant BH, dat is als 2 Δ BKN tot Δ BHO. |
| Maar Δ BHO = Δ ACL, dus trapezium EG + Δ ACL zal gelijk zijn aan 2 Δ BKN. En als van de laatste afgehaald wordt Δ BHO, en van de eerste Δ ACL, blijft over Δ BKN + trapezium HN is gelijk aan trapezium EG, en insgelijks met de overige. |
| Dus de figuur ingeschreven in de sector + alle trapezia HN = de figuren ingeschreven in het cissoïde-oppervlak. Maar de figuur in de sector met |
[ 172 ]
|
alle KND erbij, en evenzo de trapezia HN met alle KND erbij, dit alles tegelijk bij elkaar overtreft de sector + oppervlak HXMK. Dus de figuur in de sector + de trapezia HN, dat is de figuur in de cissoïde met oppervlak Ω erbij, zal ver overtreffen de sector + oppervlak HXMK. Maar het oppervlak van de Cissoïde zelf + Ω wordt bij hypothese gelijkgesteld met sector BKM + oppervlak HXMK. Dus een figuur in de Cissoïde zal groter zijn dan het oppervlak van de Cissoïde zelf, wat absurd is.
|
c) |
| |
| d) |
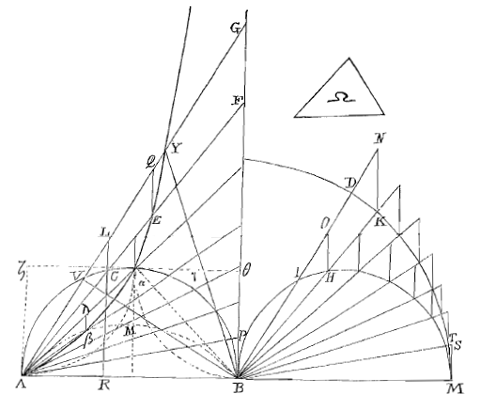
| Laat nu gezegd worden dat het oppervlak AEYGB groter is dan de sector BDM + het oppervlak IHMD en laat het overschot Ω zijn. Dan ga ik nu om de sector een figuur beschrijven, zodat alle DKN tweemaal genomen kleiner zijn dan het overschot Ω. En met evenveel trapezia omschrijf ik het oppervlak van de Cissoïde. |
| Zoals eerder werd aangetoond is trapezium EG = Δ BKN + trapezium HN. Dus de hele figuur rond de Cissoïde omschreven is gelijk aan de rond de sector omschrevene + alle trapezia HN e). Maar als hiervan afgenomen worden tweemaal alle tandjes DNK, zal het overblijfsel kleiner zijn dan sector BDM + oppervlak IHMD (want door eerst af te nemen alle DNK van de bij de sector omschreven figuur, blijft over sector BDM; maar door dezelfde DNK af te nemen van de trapezia HN, zijn alle overblijfsels tegelijk samen kleiner dan dan oppervlak IHMD; ja, ze zijn alle samen pas gelijk aan oppervlak IHMD als de OHI weer zijn toegevoegd). |
|
Dus als Ω hiervan wordt afgenomen, namelijk van de figuur om de sector + de trapezia NH, dat wil zeggen van de figuur omschreven bij het oppervlak van de Cissoïde, zal het overblijfsel veel kleiner zijn dan sector BDM + oppervlak IHMD. Maar er werd gezegd dat het oppervlak van de Cissoïde zelf, zonder Ω, eraan gelijk was. Dus het oppervlak van de Cissoïde zal groter zijn dan een omgeschreven figuur ervan, wat absurd is.
Nu dit bewezen is, dat het oppervlak AEYGB = 3 × het segment BVC + Δ AVB, is gemakkelijk te bewijzen dat het oneindige oppervlak AEYBG gelijk is aan driemaal de halve cirkel AVB.
c) Naast deze figuur staat: BαβAB = 3 Bαγ. Maar  AαB − BαβAB − Bαγ = AVαβA dus Aαβ − 4 Bαγ = AVαβA. Maar Aαβ − 4 Bαγ =  ζB ÷ Aαβ. Dus enz. [Chr. Huygens.] d) De letters F en E moeten gezet worden waar staat G en Y, omdat het oppervlak weer genoemd moet worden zoals eerder. Evenzo K en H in de plaats van N en O. [Chr. Huygens.] e) NB. dat het laatste wat bij de Cissoïde is omschreven Δ APB is (en niet een trapezium), gelijk aan Δ BSM bij de sector. [Chr. Huygens.] |
[ 173 ]
|
f) Ik heb het bewijs hiervan aan de heer de Sluse 5) gestuurd; maar dit hier is mooier. Ik heb het aan de heer Wallis gestuurd, die het heeft laten drukken in zijn verhandeling over Mechanica 6). [Chr. Huygens.] 7) 5) Het schijnt dat Huygens heel deze noot later heeft toegevoegd, en dat deze betrekking heeft op brief No. 487 [28 mei 1658 (in Ansterdam, zonder aantekeningen, "een proeve", heel mooi opgeschreven); R. F. de Sluse had hem op 14 maart 1658 geschreven over de cissoïde, zie No. 473]. 6) Dit werk werd pas later gedrukt onder de titel: J. Wallis Mechanica: sive, de Motu, Tractatus Geometricus, Londini 1670 [zie noot 1]. 7) De laatste zin is met potlood geschreven door Chr. Huygens. |
|
J. Wallis aan Christiaan Huygens.11 juli 1658. [<]Daar naar uw Nederlanden, zeer nobele heer, spoedig zal vertrekken de weledele heer Ball 1) (zoon van de heer Peter Ball 2), gulden ridder) heb ik het verzoek gedaan dat hij u namens mij zeer beleefd groet; en ook tegelijk aan u overhandigt de 'Briefwisseling' 3) die nu onlangs door mij is uitgegeven, en ik verzoek u deze welwillend te aanvaarden. En als u bovendien deze weledele heer, die vertrekt om bij u te studeren, vriendelijk met diensten zult ondersteunen, naargelang de zaak zich zal voordoen, weet dan dat dit mij zeer dankbaar zal stemmen, en zo moet u niet denken dat u deze dienst zult besteden aan iemand die het niet verdient of ondankbaar is; en weet dat, als ooit de zaak zich zal voordoen dat er aanleiding gegeven wordt aan vrienden van u, wie dan ook, iets dergelijks te betonen, ik in geen geval zal nalaten deze zeer gaarne aan te grijpen. En dit is het waarvoor ik tijd heb u voor het ogenblik lastig te vallen, en tegelijk verzoek ik u voort te gaan met mij genegen te zijn, en te begunstigen Zeer nobele heer
1) Peter Ball [1638 - 1675] studeerde in 1659 medicijnen te Leiden; behaalde zijn graad in Padua, 1660; werd een van de eerste leden van de Royal Society; nam in 1665 met zijn broer William [>] deel aan de waarneming van Saturnus. 2) Sir Peter Ball, Knight, overleed in 1680. 3) Commercium Epistolicum de quaestionibus quibusdam mathematicis, 1658 [Wallis, bij Opera II, 1656 en 1693], in-4o. De correspondentie liep van 7 maart 1657 tot 13 juli 1658, tussen W. Brouncker, Kenelm Digby, P. de Fermat, de Frenicle, Joh. Wallis, Fr. van Schooten, en anderen; bevat 47 brieven n.a.v. de uitdaging van Fermat. (Zie de brieven No. 372 en 374 [<]). | ||||||||||
|
Christiaan Huygens aan J. Wallis.6 september 1658 (Concept). 1)6 Sept. 2) 1658. Omdat u niet ophoudt mij herhaaldelijk deelgenoot te maken van uw zeer mooie werken, beken ik dat ik u zeer veel verschuldigd ben en dat ik het nog niet kan aflossen. Maar toch heeft het me aan dankbaarheid niet ontbroken, al heb ik vrij lang nagelaten deze te betuigen in aan u verzonden brieven, maar twijfelt u er niet aan, vraag ik u dringend. Vorig jaar heb ik drie werken 3) van u ontvangen, die de heer Trommius [<] overbracht, en nu weer
1) Met een exemplaar van zijn Horologium. 2) Eerst had Chr. Huygens geschreven: 28 augustus, maar hij streepte deze datum door. 3) a) Mathesis Universalis, 1657. b) Adversus Meibomium de proportionibus Dialogum, 1657. c) Hobbiani Puncti Dispunctio, 1657. [ De eerste twee in Operum mathematicorum pars prima, 1657. Ex. GWLB bevat een aantekening van Chr. Huygens: nr. 507. Pars altera (1656) heeft op de titelpagina "Don. aut." in handschrift, waarschijnlijk van Huygens; en meer marginalia: op p. 107 (nr. 191) en 111 (195) van 'De sectionibus conicis', en in 'Aritmetica infinitorum': nr. 203 (doorstreping ook in ander ex.), p. 3/215, 10/222, 43/255, 46/258, 76/288, 77/289, 83/295, 89/301, 96/308, 106/318, 134/346, 178/390, 179/391, 9/427. 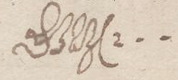 De laatste aantekening in pars altera, onder 'Finis'. Het lijkt: SJWH 2 . ., Schooten, John Wallis, Huygens.] |
[ 211 ]
|
dat nieuwste 4), van de heer Ball, waardoor het zo is dat ik me niet genoeg kan verbazen over die vruchtbaarheid van uw buitengewone verstand, die ook des te groter schijnt zo dikwijls als ik haar vergelijk met onze traagheid. Dat de leugengeschriften van Hobbes en Meibom door u bedwongen worden zoals ze verdienen, was mij uit naam van de gehele wiskunde welkom. Wat tegen deze laatste door Lange is uitgegeven 5) in Denemarken, en weer tegen Lange door Meibom 6) hebt u daarna gezien, denk ik; en ook al ziet de één scherp als een lynx de misslagen van de ander, voor die van zichzelf zijn ze even zwakziend. De verhandeling van Aynscom heeft u in elk geval bereikt, naar u te kennen geeft 7), en dat deze ook op dit gebied geen nutteloze moeite op zich genomen heeft ben ik met u eens. Wat hij echter tegen mijn 'Onderzoek' aangevoerd heeft, heb ik al lang geleden met de uitgave van een brief weerlegd 8), waarin ik me met name ook op uw gezag heb beroepen. Maar dit scheen niet van zo groot belang dat u er tijd aan zou besteden om het te lezen. Van de andere kant heb ik uit mijn brieven 9) gezien dat u in dat scherpe hekelschrift tegen Hobbes enige regels hebt laten uitkomen, waarvan ik liever wilde dat het niet gebeurd was, maar het kan niet meer ongedaan gemaakt worden.*) De 'Briefwisseling' die u nu onlangs zond heeft me zeer veel genoegen gedaan, en ik heb het werk niet uit handen gelegd voordat ik het van begin tot eind gelezen had. Ik voor mij had niet geweten dat onder u met zoveel hartstocht gestreden werd over die rekenkundige problemen. Veeleer had ik daarover dezelfde mening als u, die u naar ik zie ook vaker hebt uitgedrukt a), dat aan dergelijke zaken geen kostbare uren besteed moeten worden tenzij omdat er geen gewichtiger zaken zouden zijn, waarvan er zich zeker in de meetkunde zeer vele aanbieden. Ondertussen weiger ik niet, uitbundige lof voor scherpzinnigheid met recht toe te kennen aan ulieden, die niet langs één weg iets bereikt hebt dat door de zeer scherpzinnige heer Fermat beschouwd is als door niemand b) anders te onderzoeken. Meer dan de overige beviel me die methode, van u of van de doorluchtige Brouncker, en u duidt dit niet met voldoende zekerheid aan, uiteengezet op pagina 71; waaruit u echter geenszins juist opmaakt, lijkt mij, op pagina 83: dat een of ander kwadraat gegeven is dat, vermenigvuldigd met een getal dat geen kwadraat is, met de eenheid erbij een kwadraat maakt. Want als de bewerking volgens die methode wordt aangepakt, weet u helemaal niet hoe lang u moet doorgaan met die posities voordat u het gevraagde krijgt, daarom kunt u er in het geheel niet zeker van zijn of u dit ooit zult bereiken. De verschillen b, c, d, enz. zijn, zegt u op pagina 82, hele getallen en continu afnemend, dus tenslotte moet noodzakelijk bij de eenheid uitgekomen worden. Maar in werkelijkheid zijn het slechts volgens uw hypothese hele getallen, en daarom lijkt u te veronderstellen wat te bewijzen was. Overigens heeft ook Fermat naar ik meen dit niet beter kunnen bewijzen, omdat hij geheel tevreden is met uw oplossing [p. 96]. Frénicle was althans enige tijd van mening dat het probleem niet voor elk willekeurig gesteld getal oplosbaar was. Vandaar dat er in de lijst van pagina 149°) geen regel is die overeenkomt met het getal 33, en zelfs stond er 0 in het handschrift van die brief geschreven 10). Maar later heeft hij deze fout verbeterd 11). Waaruit ook lijkt te kunnen worden opgemaakt,
4) Zie brief No. 497 [<]. 5) No. 445, noot 5: W. Langius. Epistola ad Marcum Meibomium. Hafniae. 1656. in-4o. [De Veritatibus Geometricis Libri II.] 6) No. 445, noot 4: M. Meibomius. Responsio ad Wilh. Langii ad se epistolam. Hafniae. 1657. in-folio. 7) De brief is niet gevonden. 8) Brief No. 338 [T. 12, 263]. 9) Zie No. 272 [en No. 337]. [ *) Due correction for Mr. Hobbes, 1656, txt. Antwoord: Stigmai ... Markes ..., 1657, txt.] a) In de marge staat hier: "Dat zo'n kwadratuur geen bewijs is" [Chr. H.]. b) "wat zou ik ..." [Chr. H.]. [ °) Op p. 149 geeft Frans van Schooten een citaat uit brief No. 386 (21 april 1657) van Huygens.] 10) Zie brief No. 383 [Mylon]. 11) Zie brieven No. 388 [Mylon] en 389 [Frenicle]. |
[ 212 ]
|
waarop u doelde op pagina 136*), dat zijn methode niet even handig was als die latere van u. Ik had alleen een regel gevonden, bijna dezelfde als die u op pagina 57 en elders aanvoert; evenzo ook hoe, als één kwadraat gevonden is, talloze andere kunnen worden gevonden, geheel zoals op pagina 39 bij het midden. Die ik toen aan Mylon 12) heb meegedeeld. Het vraagstuk over de derde macht, die opgeteld bij zijn delers een kwadraat maakt, heb ik niet aangeraakt, daar ik wel inzag dat in deze zaak slechts enige bekortingen gevonden konden worden, die door u inderdaad uitstekend zijn onderzocht op pagina 103 en volgende. En we zijn u niet weinig verschuldigd omdat u hebt laten zien dat dit alles niet van zoveel gewicht is als Fermat en Frenicle het hebben willen beoordelen, en omdat u duidelijk gemaakt hebt wat zij voor een mysterie hielden. Laten zij daarom nu maar afzien van de rekenkundige vraagstukken, en omdat u voor hen een leidsman bent, laten ze zich opmaken ons eens dingen uit te leggen die hun lof toebrengen, en ons genoegen. Want ook ik vind dat het de moeite waard is, wonderlijke eigenschappen van getallen te bewijzen, waarbij heel uitzonderlijk is die, welke de brief van Fermat aan het eind van pagina 185 vermeldt. Maar die op pagina 186, "Alle machten van het getal 2" enz.°), lijkt die u voldoende zeker, om iemand te laten nadenken over een bewijs ervan? Ik verbaas me erover hoe Fermat zo vol zelfvertrouwen heeft durven zeggen dat deze waar is, aangezien geen sterveling dit lijkt te kunnen vaststellen, zelfs niet met inductie. Want dat de zaak slaagt voor de eerste 4 of 5 getallen geeft niets dan een geringe waarschijnlijkheid. Uw op pagina 110 voorgestelde theorema is zeer elegant; toch had die eigenschap van een stomphoekige driehoek met 120 graden veel korter op een andere manier bewezen kunnen worden. Bij een ander, op pagina 169: ofschoon u bedacht dat het betrekking heeft op de conchoïde, schijnt u niet opgemerkt te hebben dat de oneindige oppervlakte van de conchoïde ook een oneindige grootte heeft, ik herinner me dat ik dit ooit bewezen heb. Van twee oneindige grootten kan immers niet goed gezegd worden dat de ene groter is dan de andere, of in een of andere verhouding staat tot de andere.
Ik zend hierbij de beschrijving van ons uurwerk 13), waarvan ongetwijfeld het gerucht u al bereikt heeft. 
[ *) Op p. 136 verwijst Wallis naar een brief van Fr. van Schooten met "Huygens vond de methode zo bewerkelijk dat hij ervoor terugdeinsde", zie brief No. 386.]12) Deze brief van Huygens aan Mylon (tussen 1 febr. 1657 en 7 maart 1658) is niet gevonden. [ °) "... waarvan de exponenten termen zijn van de Meetkundige reeks van hetzelfde getal 2, met de eenheid toegevoegd, zijn priemgetallen"; zie Fermatgetal.] [ #) Zie voor Huygens' bewijs No. 483 hierboven. ] 13) Horologium, zie brief No. 511, noot 2 [<]. |
[ 213 ]
|
Want ook aan uw mensen heb ik het laten zien, aan de heer Williamson 14) en anderen, en ik weet dat er al lang geleden enige van dit soort automaten naar Engeland vervoerd zijn. Zeer veel bezigheid gaf me deze uitvinding, of liever de onbeschaamdheid van misdadige mannen 15) ter gelegenheid ervan, en het was er de oorzaak van dat ik de lang beloofde sterrenkundige verhandeling over Saturnus nog niet kon uitgeven. Ondertussen kan ik niet anders dan antwoord geven op wat u bijgeschreven had in uw brief aan van Schooten, afgegeven op 4 februari. Namelijk dat de eerste fase van  [Saturnus] die schitterde na de bolvormige, mijn vermoeden steunde, maar wat later dan het door mij verwacht was; wat beide waar is. En toch is die hypothese die in mijn anagram bevat is, en waarvan de uitleg misschien bij u ook al doorgedrongen zal zijn, geenszins verzwakt, maar van dag tot dag wordt bevonden dat deze meer en meer met de waarheid overeenstemt. U hebt terecht opgemerkt dat het verzinsel van Hevelius hierbij zeer weinig overeenstemt met de waarnemingen, niet alleen met die welke volgden op de uitgave van zijn boek [<], maar ook met de voorgaande. Het ontbreekt hem kennelijk aan voor deze waarnemingen geschikte telescopen; hij heeft immers de begeleider ook nog niet kunnen zien; veel minder nog de donkere lijn die het midden van de Saturnusschijf bezette, toen hij rond en zonder armen te zien was, die nu echter iets naar beneden is afgeweken. Dit heb ik willen opmerken opdat u er niet aan twijfelt dat deze tenminste door mij bekeken is. Enige maanden geleden is mij uit Sicilië gebracht een of ander Systeem van Saturnus, uitgegeven door een sterrenkundige die mij voordien onbekend was, Johannes Hodierna [<], waarbij ook een brief gevoegd was waarin hij me aanspreekt. Hij had namelijk mijn waarneming van de maan van Saturnus [<] gezien, en opdat hem niet het gras voor de voeten weggemaaid zou worden had hij dat systeem onmiddellijk daarop laten drukken. Doch het is ook nog wat dwazer dan het verzinsel van Hevelius, en verdient het nauwelijks dat ik het voor u uiteenzet. Laat ik het toch in enkele woorden beschrijven. Hij denkt dat Saturnus de vorm heeft van een langwerpige sferoïde, waarin twee donkere vlekken zijn die ons die tussenruimtes doen zien die tussen de schijf in het midden en de kromming van de oren liggen. En dat tweemaal per dertig jaar de top van de sferoïde naar ons gericht is, en dat daardoor Saturnus zich dan rond vertoont. Maar uit deze hypothese zouden enige andere fasen volgen dan die waargenomen worden met telescopen van de betere soort, waarvan ook deze beste man zich afvraagt of hij er te weinig van voorzien is, en hij bekent dat de satelliet voor hem nog niet zichtbaar was. Wat in uw anagram wil zeggen die uitdrukking Quasi lunando vehitur (beweegt zich als met een maansikkel [<]), daar ben ik nog niet achter kunnen komen. Ik zou evenwel door u op de hoogte gesteld willen worden*), aangezien ik besloten heb in mijn verhandeling ook melding te maken, zoals billijk is, van dit 'in het vizier hebben' bij de uwen. Als de 'Problemen' [<] van de anonieme Fransman over de cycloïde-lijn ook bij u zijn aangekomen, schrijft u
14) Sir Joseph Williamson (1633 - 1701), Secretary of State en lid van de Privy Council tot 1678. 15) Zoals Simon Douw [<]. [ *) In zijn lange antwoordbrief van 1 jan. 1659 geeft Wallis toe dat hij met zijn anagram een spelletje heeft gespeeld, zie p. 306 hierna.] |
[ 214 ]
|
mij dan alstublieft wat voor oordeel men er bij u over heeft, en of het oplossen door iemand geprobeerd is. Ik heb, toen ik de meeste ervan gevonden had, over de andere gevraagd of de auteur zelf een oplossing ervan zou durven beloven; gemakkelijk kunnen immers onmogelijke bedacht worden, en waarvan toch niemand onomstotelijk kan bewijzen dat ze het zijn. Overigens heb ik geen antwoord ontvangen, vandaar dat ik hen ervan verdenk dàt van ons te vragen, waarvan ze de hoop opgeven dat zij het zelf kunnen vinden. Dus het ga u goed, uitnemende heer, en vergeef deze al te grote uitvoerigheid, zoals ook de vrijheid die we ons herhaaldelijk hebben aangematigd bij het weerleggen van iets van u. Wat ik wel zou laten als ik uw denken niet zou waarderen in vergelijking met het mijne. Verder, dat hij met een geldprijs onze ijver prikkelt, lijkt het u niet prachtige dikdoenerij? Maar het is tijd dat ik aan deze breedsprakige brief een eind maak.
|
[ 296 ]
|
J. Wallis aan Christiaan Huygens.1 januari 1659.
De brief die u me had gestuurd, weledele heer, gedateerd op 8 augustus 1), heb ik zeer laat ontvangen. In elk geval werd hij tegen 5 november hier naar Londen gebracht, bijna op dezelfde tijd dat ik op weg was naar Londen, zodat ik hem niet eerder had gezien dan toen ik hem, teruggekeerd naar huis, op 11 december hier vond. Deze vertraging onderweg betreur ik om meer dan één reden. Wat u nu tegen het eind ter verontschuldiging hebt verzocht, dat ons niet zou mishagen de vrijheid die u hebt gebruikt om iets in ons werk af te keuren: het is er zo ver van verwijderd dat ik u dit kwalijk neem, dat ik het integendeel houd voor een teken van eer en vriendschap van een zo groot man, en zeer bekend met deze zaken, vertrouwelijk bejegend te worden, die ook indien ik ergens een fout heb gemaakt zowel in staat is het met scherpzinnigheid terstond met eigen ogen te doorzien, als het met genegenheid en als een vriend aan te wijzen. Wat u hebt over Lange en Meibom: ik heb het geschrift van Lange 2) wel gezien, maar nog niet doorgelezen; doch wat Meibom er tegenover heeft gesteld 3) heb ik zelfs niet gezien; zoals ook niet de Brief die u zelf tegen Aynscom hebt geschreven 4); waarin ons gezag, hoe het ook mag zijn, wel door u gebruikt kan worden, ik feliciteer u ook. Maar ondertussen vraag ik ook verontschuldiging omdat ik het uwe zonder uw medeweten gebruikt heb 5) (al is de naam niet genoemd), vooral aangezien ik begrijp dat het u niet beviel. |
|
Dat nu dat hekelschrift tegen Hobbes zo vals was, is niet door mijn manieren maar door noodzaak afgedwongen. U ziet immers, naar ik geloof, uit mijn andere geschriften, hoe vreedzaam ik zowel met anderen van mening kan verschillen, als degenen die met mij van mening verschillen kan verdragen. Maar dit werd gedaan door onze Leviathan (zoals uit zijn geschriften, vooral de Engelse, makkelijk is op te maken) om met alle heftigheid los te stormen op zowel onze Academies (en niet alleen de onze maar ook alle in het algemeen, zowel oude als recentere) alsook vooral op de kerkdienaren, en hun hele ambt, en ook de religie in het algemeen, en die volledig te gronde te richten. Alsof de Christelijke wereld in de Filosofie of in de Religie niets verstandigs kent en niets dat niet belachelijk is; en ze juist de Religie niet hebben begrepen omdat het geen Filosofie is, noch de Filosofie omdat het geen Wiskunde is. Het is daarom noodzakelijk geacht dat, op de weg terug, tenminste iemand van de Wiskundigen aantoont hoe weinig hij zelf van Wiskunde heeft begrepen (waaruit hij zijn overmoed heeft gehaald),
a) Rcp. 16 Jan. 1659 [Chr. Huygens, datum van ontvangst]. 1) Het gaat om No. 512, met op het concept 28 augustus doorgestreept en vervangen door 6 september. 2) Zie No. 445, n.5. 3) Zie No. 445, n.4. 4) Zie No. 338, n.1. [Ned.] 5) Zie hierboven No. 512, n.3. |
[ 297 ]
|
alswel dat dit zo gebeurt dat we niet worden afgeschrikt door zijn hooghartigheid, waarvan we weten dat die alle venijn en vuil zal uitbraken. Maar tot dusver hierover. Over Meibom en de Fransen hebben we niet op die manier geschreven, en we hebben ze niet anders behandeld dan edele en oprechte heren; en ik geloof niet dat er iets is dat ze wel terecht op hem hebben aan te merken. Of Meibom iets over mij in zijn geschriften tegen Lange heeft ingevlochten, of ook afzonderlijk heeft geschreven, weet ik niet. Maar indien het zo is, zult u mij een genoegen doen als u het aanwijst en, als u het een geschreven werk is, dit opstuurt (wat gedaan kan worden via uw boekhandeleaar de heer Brown 6) naar de heer Underhill 7) te Londen); ik geloof namelijk dat het nog niet te koop is bij onze boekhandelaren. Onze 'Briefwisseling' 8) met de weledele Fransen Fermat en Frenicle, u ziet hoe deze is begonnen*). Niet slechts tegen wil en dank ben ik op die talloze flauwigheden ingegaan, en heb ik me er pas laat in ernst op toegelegd, en alleen na uitdaging (wat uit die brieven blijkt), vooral daarop dat Frenicle over allen lijkt te triomferen in zijn Voorwoord bij zijn Oplossingen°), waarvan ik ook heb gemeend dat er misschien niet ondoordacht tegen ingegaan moest worden; wat we ook gedaan hebben. |
|
Maar ook heeft hij zich daarmee niet helemaal te goeder trouw (tenzij ik het verkeerd zie) met ons gemeten (wat ook anderen misschien zullen opmerken die er niet van op de hoogte zijn); zij lossen immers helemaal niets zodanig op (zelfs niet hun eigen Problemen), dat iemand er geleerder of kundiger van wordt. Ze geven althans niets dan enige bijzondere getallen die aan het gevraagde voldoen, ondertussen juist de methode verbergend waarmee zij die zelf kunnen laten zien, of anderen andere, en ze geven zelf niet de algemene regels die ze van ons verlangen. Ze zetten de zaak namelijk op voor uiterlijk vertoon, veeleer dan voor de vooruitgang van de Wiskunde; terwijl wij daarentegen ook antwoorden geven en de grondslagen van de antwoorden bekend maken, wat we hun tot nu toe niet kunnen afdwingen. Wat nu van mij is, en wat van de illustere burggraaf Brouncker, hoewel het niet zo makkelijk overal te bepalen is, daar we elkaar niet zelden in wederzijdse brieven een handvat hebben aangereikt, en hij het zijne meestal door mij heeft laten uitleggen; toch heb ik er oprecht voor gezorgd, wat het zijne is aan hem toe te kennen. En dus ook onder andere die Methode die op pagina 71 voorkomt, die meer van de illuster Brouncker is dan van mij (wat ik daar voldoende aangegeven meende te hebben) al heeft hij deze daarna aan mij overgelaten om uiteen te zetten; die ook veel krachtiger is dan de mijne die eraan voorafgegaan was, maar die hij nog niet had gevonden toen ik voor hem de eerste had beschreven. |
|
Geen van beide methoden lijkt echter zo zwak, dat ze niet voor krachtiger gehouden wordt dan het kale ten toon stellen van enige getallen (wat door Frenicle is gedaan #)). Vooral aangezien elk van beide iets laat zien wat Frenicle niet had verwacht, namelijk dat de Analytische methode (die hij in die tijd in een naar hier gezonden brief geringschatte, tenminste bij dit soort vraagstukken, en voor zijn gevoel) dit ook kan opleveren. En zeker merk ik dat die methode van hem (welke dan ook) of die nu van Fermat is of van Frenicle, duidelijk onderdoet voor die van ons, daar geen van hen de zijne tot nu toe heeft willen prijsgeven, wat ze heel zeker zouden doen als ze daarmee iets
6) Samuel Broun. Zie brief No. 307, n.1. 7) Thomas Underhill was boekhandelaar te Londen van 1641 tot 1658, eerst in Word-Street, 'The Bible', en daarna in St. Paul's Church-Street, 'The Anchor and Bible'. 8) Zie hierboven brief No. 497, n.3. [Op p. 1: "A challenge from M. Fermat, for D. Wallis", met het al op p.212 genoemde probleem "Een derde macht te vinden, die opgeteld bij zijn delers een kwadraat maakt", voorbeeld: 343, dat maakt 400.] [ *) Jacqueline Stedall, 'John Wallis and the French', Hist. Math. 39 (2012) 265-279.] [ °) Bernard Frénicle de Bessy, Solutio duorum problematum circa numeros cubos & quadratos, Par. 1657. Probleem 1: zie vorige noot (nu daarbij: "400, wat ook opgeteld bij zijn delers een kwadraat geeft: 961"). Probleem 2: "een kwadraat vinden, dat opgeteld bij zijn delers een derde macht maakt".] [ #) In het werk van de vorige noot, 'Problemata duo, numerica': 424 462 145 606 577 000 is derde macht van 751 530, met de som van zijn delers erbij ..., wat het kwadraat is van ...; evenzo voor een oneven getal van 23 cijfers, derde macht van 37 200 735.] |
[ 298 ]
|
zouden hebben dat meer uitgewerkt of verscherpt is. En met een dergelijk argument zal misschien zijn te concluderen dat die algemene Regel die Fermat op pagina 6 belooft te zullen meedelen — alleen als ik dat zou wensen (wat ik dus vraag op pagina 8), maar die hij op pagina 21 uitstelt tot een volgende keer, totdat ik zelf heb laten zien wat ik over deze zaak kan leveren, en tenslotte ontwijkt hij, en hij heeft niets anders ervoor in de plaats gesteld dan een getuigenis van Roberval en van Pascal, dat hij dit kan doen, op pagina 160 — minder waard is, of althans niet meer, dan het door mij gegevene op pagina 45 en 52. Vooral daar hij ook van het gevraagde dat ik over hetzelfde onderwerp er tegenover had gezet op pagina 46, een oplossing ontwijkt. Wat u over onze gevolgtrekking op pagina 83 inbrengt, ik ontken niet dat dit waar is, wat ik ook eerder heb gezien; maar omdat het in de brief geschreven was, die eerlijk en oprecht moest worden ingevoegd, was besloten hem bij het uitgeven niet te veranderen. En ik wilde wel dat er aan het begin alleen dit werd ingebracht, dat veeleer de grondslag van een bewijs dan een volmaakt bewijs in het daar gegevene voorhanden is; in elk geval had ik getaxeerd dat Fermat nauwelijks een beter bewijs zou geven. Wat te denken is over het Theorema van Fermat (over machten van het getal twee 9)), staat voor mij nog niet vast. Dat de eigenschap van een stomphoekige driehoek met 120 graden, die ik uiteenzet op pagina 110 enz. korter kan worden bewezen, weet ik wel. Maar ik heb dat bewijs gekozen, uit verschillende die voorhanden waren, dat afhangt van de driedeling van een hoek (als zijnde elegant, al is het niet het kortste), vooral ontleend aan een verhandeling 10) die ik tien jaar geleden, over het snijden van hoeken, als oefening had opgesteld; waarin ik dergelijke eigenschappen van andere driehoeken, zowel stomphoekige als scherphoekige, met een volkomen gelijke methode bewijs. Als u liever een korter bewijs wilt, krijgt u het volgende.
Wat u hebt over het oppervlak bij een Conchoïde. Namelijk, dat ik niet lijk te hebben opgemerkt, dat die oppervlakte 9) [P. 186.] Zie brief No. 25, n.7 [Mersenne, 1647; eerder: 1640, zie Nombre de Fermat]. 10) Dit werk werd later gepubliceerd: J. Wallis, Treatise of angular sections, Lond. 1684 [in Treatise of algebra, 1685; zie p. 50]. 11) Pq betekent het kwadraat van P. 12) Wallis schrijft Q: A + C: voor (A + C)². 13) Lees: − / +. |
[ 299 ]
een oneindige grootte heeft: het is heel anders. In elk geval wist ik dat die oneindig is; het "in een gegeven verhouding verdeeld worden" kon in dezelfde zin gezegd worden,
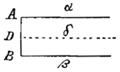als een oneindig parallellogram tussen oneindige zijden Aα en Bβ gezegd wordt in een gegeven verhouding verdeeld te worden door een evenwijdige rechte Dδ die de zijde AB in de gegeven verhouding verdeelt; of ook dat een oneindige parabool of hyperbool door de diameter in twee helften wordt verdeeld. En ik wilde met die propositie niets anders aanduiden.
Laten we nu stellen dat de rechte AD verdeeld wordt in een oneindig aantal gelijke delen, met oneindig veel punten L. Dan zullen alle AL zijn als 1, 2, 3, enz., waarvan de grootste AD is (die genoemd wordt D). En alle kwadraten 14) LK of LP zijn als √: 1 D − 1. 15) √: 2 D − 4. √: 3 D − 9. enz. |
| 1 | · | 4 | · | 9 | · | enz., dat wil zeggen als |
| √: D − 1: | √: 2D − 4: | √: 3D − 9: |
| 1 × 1 | · | 2 × 2 | · | 3 × 3 | · | enz., dat wil zeggen als |
| √ 1 × √: D − 1: | √ 2 × √: D − 2: | √ 3 × √: D − 3: |
| 1 √ 1 | · | 2 √ 2 | · | 3 √ 3 | · | enz., of |
| √: D − 1 | √: D − 2 | √: D − 3 |
| √ 1 | · | √ 8 | · | √ 27 | · | enz., of |
| √: D − 1 | √: D − 2 | √: D − 3 |
| √ | 1 | · | √ | 8 | · | √ | 27 | · | enz. Dat wil zeggen: |
| D − 1 | D − 2 | D − 3 |
|
Alle kwadraten van LB zijn een reeks van derde machten gedeeld door een reeks van omgekeerd geplaatste eerste machten; en die rechten LB zelf zijn in de verhouding van de tweedemachtswortels daarvan.
14) Het woord 'kwadraten' is hier te veel. 15) Met √: 1 D − 1. of met √: D − 1:, bedoelt Wallis √(D − 1). |
[ 300 ]
|
Omdat echter die oneindige reeks het drievoudige is van de reeks √: 1 D − 1. √: 2 D − 4. √: 3 D − 9. enz. (dit is een reeks van tweedemachtswortels van een reeks van eerste machten die omgekeerd met zichzelf wordt vermenigvuldigd), wil dat zeggen: van de halve cirkel; maar het wordt opgemaakt uit beginselen van de Arithmetica infinitorum [1656] (wat iets uitgebreider zal moeten worden aangetoond, omdat die hele zaak van directe reeksen met omgekeerde reeksen vermenigvuldigd, of erdoor gedeeld, daar maar karig behandeld wordt [p. 133-135]).*) De reeksen van eerste, tweede, derde machten enz. duiden aan a, a², a³ enz. evenzo die van tweedemachtswortels, derdemachtswortels enz. √a, √3a 16), enz. Als dus de reeks √a vermenigvuldigd wordt met de omgekeerde reeks a (dat is met de reeks D − a), ontstaat de reeks D√a − a√a, of D√a − √a³; die zal tot de reeks van gelijke°) staan als (2/3 − 2/5 =) 4/15 tot 1 (volgens de proposities 64 en 73 van Arithmetica infinitorum). |
|
Op dezelfde manier, als die zelfde reeks √a wordt vermenigvuldigd met de omgekeerde reeks a², dat is met de reeks Q: D − a: of D² − 2Da + a² ontstaat de reeks D²√a − 2Da√a + a²√a, of D²√a − 2D√a³ + √a5; die tot de reeks van gelijke staat als (2/3 − 4/5 + 2/7 =) 16/105 tot 1 (dat is in de verhouding 16/105, of 16 tot 105). En evenzo, als dezelfde reeks van tweedemachtswortels (oftewel √a) wordt vermenigvuldigd met andere omgekeerde reeksen, zullen deze volgende verhoudingen eruit voortkomen. Als namelijk de reeks √a omgekeerd wordt vermenigvuldigd |
| met de reeks | 1. | a. | a². | a³. | a4. | enz. komen er de | |||||||||||||
| verhoudingen | 2 | · | 4 | · | 16 | · | 96 | · | 768 | · | enz. | ||||||||
| 3 | 15 | 105 | 945 | 10395 | |||||||||||||||
| dat is | 2 | · | 2×2 | · | 2×2×4 | · | 2×2×4×6 | · | 2×2×4×6×8 | · | enz. | ||||||||
| 3 | 3×5 | 3×5×7 | 3×5×7×9 | 3×5×7×9×11 | |||||||||||||||
|
Als deze dan voor de even plaatsen gehouden worden, en de tussengelegen oneven plaatsen worden aangevuld, door te stellen in plaats van de derde (tussen 1 en a), voor de reeks √a omgekeerd vermenigvuldigd met de reeks √a, de verhouding 1 / (2 ) 17) (volgens propositie 167 van Arithmetica infinitorum): zoals de verhouding van de vierde plaats de verhouding van de tweede vermenigvuldigt met 2/5, en de verhouding van de zesde deze met 4/7, enz. is duidelijk (uit de opeenvolging van de reeks) dat de verhouding van de vijfde de verhouding van de derde vermenigvuldigt met 3/6; en evenzo bij de overige, naar deze vorm. Namelijk, de reeks √a omgekeerd vermenigvuldigd met |
| de reeks | 1 | · | 1. | √a. | a. | √a³. | a². | √a5. | a³. | enz. geeft | ||||||||||||||||
| √a | ||||||||||||||||||||||||||
| de verh. | 1 | ) | 1 | 18) | · | 2 | · | 1 | · | 2×2 | · | 1 | × | 3 | · | 2×2×4 | · | 1 | × | 3 | × | 5 | · | 2×2×4×6 | · | enz. |
| 4 | 2 | 3 | 2 | 3×5 | 2 | 6 | 3×5×7 | 2 | 6 | 8 | 3×5×7×9 | |||||||||||||||
|
[ *) Het vervolg (tot halverwege p. 304) staat met enkele uitbreidingen in J. Wallis, Tractatus duo (1659), Posterior (brief aan Chr. Huygens), p. 82-90 (met andere letters in fig. 22), na het antwoord op brief No. 625.] [ °) Zie Wallis 1659, p. 82: "series Aequalium sive totidem D√D", evenveel keer D√D.] 16) Lees: ³√a. 17) Wallis gebruikt dit teken voor 4 / π. [Vermeld in Wallis 1659, p. 17: cirkel / d².] 18) Wallis schrijft 1/4 ) 1/2 voor 1/2 : 1/4 [dus voor π / 2].
|
[ 301 ]
|
Waaruit, voor de zaak die hier behandeld wordt, tenminste dit is te kiezen, dat de reeksen √a en √a³ omgekeerd met elkaar vermenigvuldigd, tot de reeks van gelijke staan als (1 / (2 ) × 3/6 =) 1 / (4 ) tot 1.
Verder, zoals we de reeks √a al hebben afgewogen, zullen we evenzo de reeks √a³ afwegen. Als deze namelijk omgekeerd wordt vermenigvuldigd met de reeks a, dat is met D − a, geeft dit de reeks D√a³ − a√a³, of D√a³ − a√a5, waarmee overeenkomt de verhouding (2/5 − 2/7 =) 4/35. En evenzo bij de overige, naar deze vorm. |
| met de reeks | 1. | a. | a². | a³. | a4. | enz. geeft de | |||||||||||||
| verhoudingen | 2 | · | 4 | · | 16 | · | 96 | · | 768 | · | enz. | ||||||||
| 5 | 35 | 315 | 3465 | 45045 | |||||||||||||||
| dat is | 2 | · | 2×2 | · | 2×2×4 | · | 2×2×4×6 | · | 2×2×4×6×8 | · | enz. | ||||||||
| 5 | 5×7 | 5×7×9 | 5×7×9×11 | 5×7×9×11×13 | |||||||||||||||
|
Als deze dan voor de even plaatsen gehouden worden, en de oneven plaatsen worden aangevuld, door te stellen (volgens het zojuist gedane onderzoek) op de derde plaats (tussen 1 en a) de verhouding 1/(4 ): zoals de verhouding van de vierde plaats de verhouding van de tweede vermenigvuldigt met 2/7, en die van de zesde deze met 4/9, enz., zo vermenigvuldigt de verhouding van de vijfde plaats de verhouding van de derde plaats met 3/8, en de verhouding van de derde de verhouding van de eerste met 1/6; en evenzo bij de overige, naar deze vorm. Namelijk, de reeks √a³ omgekeerd vermenigvuldigd met de |
| reeks | 1 | · | 1. | √a. | a. | √a³. | a². | √a5. | a³. | enz. geeft de | |||||||||||||||
| √a | |||||||||||||||||||||||||
| verh. | 1 | ) | 1 | · | 2 | · | 1 | · | 2×2 | · | 1 | × | 3 | · | 2×2×4 | · | 1 | × | 3 | × | 5 | · | 2×2×4×6 | · | enz. |
| 6 | 4 | 5 | 4 | 5×7 | 4 | 8 | 5×7×9 | 4 | 8 | 10 | 5×7×9×11 | ||||||||||||||
|
Aangezien nu de reeks √a³ omgekeerd vermenigvuldigd met de reeks 1/√a, dat wil zeggen de reeks √a³ gedeeld door de reeks √a, staat tot de reeks van gelijke als 1/6 ) 1/(4 ) tot 1, dat is als 6/(4 ) of 3/(2 ) tot 1, zal (in het hier behandelde geval) het oppervlak ADFEB staan tot het vierkant van diameter AD, als 3/(2 ) tot 1, of als 3 tot 2 . Maar (volgens propositie 167 van Arithmetica infinitorum): de halve cirkel ACD staat tot hetzelfde vierkant van de diameter, als 1 tot 2 . Dus die oppervlakte is het drievoudige van de halve cirkel. Wat te bewijzen was.
|
[ 302 ]
|
AD, een oneindige grootte heeft; tenslotte dat het zwaartepunt nergens is. En wel als volgt. Met AO als evenwichtslijn gesteld, zullen de momenten*) van de rechten BL zijn de reeks, samengesteld uit de reeks van de grootten van BL, dat is √{a³ / (D − a)}, en de afstand AL, dat is a; en dus de reeks a√{a³ / (D − a)}, of √{a5 / (D − a)}. De verhouding hiervan tot de reeks van gelijke, namelijk tot het moment van het vierkant van de diameter opgehangen aan het punt D, wordt opgemaakt als volgt. De reeks √a5 omgekeerd vermenigvuldigd |
| met de reeks | 1. | a. | a². | a³. | a4. | enz. geeft de | |||||||||||||
| verhoudingen | 2 | · | 2×2 | · | 2×2×4 | · | 2×2×4×6 | · | 2×2×4×6×8 | · | enz. | ||||||||
| 7 | 7×9 | 7×9×11 | 7×9×11×13 | 7×9×11×13×15 | |||||||||||||||
|
En zo, aangezien de reeks √a, omgekeerd vermigvuldigd met de reeks √a5, de verhouding geeft (zoals boven) van 1 / (2 ) × 3/6 × 5/8, dat is 5 / (32 ), zullen we de plaatsen ertussen aanvullen naar analogie, tot de volgende vorm. Namelijk, de reeks √a5 omgekeerd vermenigvuldigd met de |
| reeks | 1 | · | 1. | √a. | a. | √a³. | a². | √a5. | a³. | enz. geeft de | |||||||||||||||
| √a | |||||||||||||||||||||||||
| verh. | 1 | ) | 5 | · | 2 | · | 5 | · | 2×2 | · | 5 | × | 3 | · | 2×2×4 | · | 5 | × | 3 | × | 5 | · | 2×2×4×6 | · | enz. |
| 8 | 32 | 7 | 32 | 7×9 | 32 | 10 | 7×9×11 | 32 | 10 | 12 | 7×9×11×13 | ||||||||||||||
|
Dus de momenten van alle LB, dat wil zeggen het moment van het oppervlak ADFEB in zijn stand (ten opzichte van de evenwichtslijn AO), staat tot de momenten van evenveel AD op de afstand AD, dat wil zeggen tot het moment van het vierkant AD, opgehangen aan het punt D: als 1/8 ) 5/32 , dat is als 5/4 tot 1, of als 5 tot 4 . En dan (wegens de grootte van de halve cirkel tot het vierkant van de diameter, als 1/2 tot 1, of als 1 tot 2): tot het moment van de zo opgehangen halve cirkel, als 5/2 tot 1, of als 5 tot 2; of, opgehangen aan N, als 5 tot 1.
Hetzelfde is op dezelfde manier af te leiden, met gesteld (aan het begin) DF als evenwichtslijn. Namelijk, aangezien de reeks van de grootten van LB is √{a³ / (D − a)}, en van de afstanden D − a, is de uit beide samengestelde reeks van de momenten √{a³ / (D − a)} vermenigvuldigd met D − a, dat is √{a³ met (D − a)}, of [ *) Over het begrip moment zie D. Burger en J. A. Vollgraff, 'De uitvinding van de natuurkundige formule', in Faraday 17 (1948), met op p. 95: "product van een grootte en een afstand" als vertaling van Wallis' uitleg in Tractatus duo, 1659, p. 17.] |
[ 303 ]
|
de reeks √a³ omgekeerd vermenigvuldigd met de reeks √a, waarmee overeenkomt (zoals boven) de verhouding 1/4. Dus het moment van het genoemde oppervlak in zijn stand (ten opzichte van de rechte DF) staat tot het moment van het vierkant van AD, op afstand AD opgehangen, als 1 tot 4, en zo tot het moment van de zo opgehangen halve cirkel, als 1 tot 2. Dat wil zeggen: het weegt op tegen de halve cirkel opgehangen op afstand ½ AD, dat is aan het punt N oftewel het middelpunt. Dat wil zeggen: het Cissoïde-oppervlak in zijn stand weegt op tegen de halve cirkel in de zijne, ten opzichte van de rechte DF. En dientengevolge, aangezien het Cissoïde-oppervlak het drievoudige is van de halve cirkel, zal de afstand een derde deel zijn van de afstand, dat is 1/3 DN, of 1/6 DA, en wel vanaf de rechte DF; en dan dus 5/6 DA vanaf de rechte AO, zoals tevoren. En hieruit maken we onmiddellijk op, dat het lichaam uit omwenteling van het Cissoïde-oppervlak ADFEB, tot het lichaam uit omwenteling van de halve cirkel ACD, om dezelfde rechte AO, staat als 5 tot 1 (namelijk als momenten van de vlakken ten opzichte van dezelfde rechte AO); doch dat ze gelijk zijn bij omweneling om de rechte DF (wegens de gelijke momenten van de vlakken ten opzichte van deze rechte). En nu is het wel heel opmerkelijk (ik weet niet of iemand me er eerder op gewezen heeft), dat de verhoudingen van de momenten van lijnen of vlakken, ten opzichte van een of andere rechte, en de verhoudingen van vormen ontstaan uit omwenteling daarvan om dezelfde rechte, altijd dezelfde zijn. Het bewijs is makkelijk: omdat immers beide uit dezelfde verhoudingen worden samengesteld, namelijk van grootten en afstanden. Als Tacquet dit ene punt zou hebben opgemerkt, zou hij zijn theorie (die ongetwijfeld scherpzinnig en elegant is) over Cilinders en Ringen 19) veel meer vermeerderd hebben gemaakt, misschien ook korter. Dan zou immers, om de grootte van een ring te bepalen, ontstaan uit een omwenteling van een willekeurige vlakke figuur, niets anders nodig zijn, dan de grootte van het vlak te beschouwen, en de afstand van zijn zwaartepunt tot de pool of de omwentelingsas. In elk geval is de ring gelijk aan het prisma, waarvan de basis is de voortbrengende figuur, en de hoogte gelijk aan de omtrek, die door het zwaartepunt van de voortbrengende figuur wordt beschreven. Maar dit terzijde; het zal u toch miscchien niet mishagen.
Verder, als we ons voorstellen dat het Cissoïde-oppervlak wordt gewenteld om de rechte AD, is het duidelijk dat de cirkels met de stralen LB, in kwadratische verhouding zijn met dezelfde stralen; en zo ook de reeks a³ / (D − a), die tot de reeks van gelijke, namelijk evenveel cirkels met stralen D of AD, een oneindige verhouding heeft, en dus van oneindige grootte is. Wat als volgt is af te leiden. |
| met de reeks | 1. | a. | a². | a³. | a4. | enz. geeft de | |||||||||||||
| verhoudingen | 1 | · | 1×1 | · | 1×1×2 | · | 1×1×2×3 | · | 1×1×2×3×4 | · | enz. | ||||||||
| 4 | 4×5 | 4×5×6 | 4×5×6×7 | 4×5×6×7×8 | |||||||||||||||
|
Aangezien dus de verhoudingen worden voortgezet (zoals blijkt) door de onmiddellijk eraan voorafgaande te vermenigvuldigen
19) Zie het werk van brief No. 102, n.5. [Cylindricorum et Annularium libri IV, Antw. 1651; Liber V, 1659.]
|
[ 304 ]
|
met 1/5, 2/6, 3/7, enz., moet de eerste ervan een voorafgaande vermenigvuldigen met 0/4, wat dus zou zijn 0/4 ) 1/4 ( 4/0 20). En zo zou dan dezelfde reeks a³ omgekeerd vermenigvuldigd met de reeks 1 / a, dat is de reeks a³ / (D − a), een verhouding hebben van 4 21) tot 0, wat oneindig is; en het lichaam zelf zou daarom van oneindige grootte zijn. Wat te bewijzen was. Maar daarom ook zou (zoals zojuist is aangetoond) het moment van het Cissoïde-vlak ADFEB ten opzichte van de rechte AD, staan tot het moment van vierkant*) AD, ten opzichte van dezelfde rechte, als 4 21) tot 0, dat is oneindig. En dientengevolge, terwijl dat oppervlak van een eindige grootte is, zou de afstand van het zwaartepunt oneindig zijn, dus dit is nergens. Wat we als laatste hebben willen bewijzen.
Het exemplaar van uw Horologium dat u hebt gestuurd aanvaard ik met dank; het is zeker een uitstekende en beroemde uitvinding. Ik had eerder bij de onzen gezien die uitvinding van een slinger gekoppeld aan een veer; maar het is ook bekend dat de uitvinding van u is (of het van de vakman zelf is, of van elders, weet ik niet), die slinger was echter in lengte nauwelijks groter dan drie of vier vingers (als ik het goed heb). En een geringe verandering in omstandigheden zou uw uitvinding volstrekt niet kleiner maken, aangezien het naar ieders wens gemaakt kan worden. En of hij nu aan een gewicht of aan een veer wordt gekoppeld, die toepassing van de slinger zal hoe dan ook van u zijn. De tegenwerpingen die u vermeldt over de kleine ongelijkheid die er nog is, zowel wegens de veranderde boog van de slinger, als ook wegens de kracht die op de slinger wordt uitgeoefend door het gewicht, kwamen beide bij mij op, toen ik voor het eerst van de zaak had gehoord; maar ook heeft dezelfde oplossing als die u ook gebruikt, elk van beide weggenomen, zodra ze bedacht was: dat het zo weinig is dat het terecht onbelangrijk gevonden moet worden. Doch wat Wendelinus 23) heeft ingebracht als ongelijkheid 24), is mijns inziens niet waar. En al eerder heeft van de onzen menigeen 20) Lees 1 / 0, als uitkomst van: 1 / 4 gedeeld door 0 / 4. 21) Lees 1. [ *) Lat. "quod ratio", correctie p. 635: "quadrati". Wallis 1659, p. 88 geeft ook "quadrati".] 22) Zie het stuk No. 483. 23) Godfried [Govaert] Wendelen [... 1580-1667] studeerde in Rome (1603-1604) en vestigde zich als advocaat te Parijs. In 1612 keerde hij terug naar de Nederlanden, werd priester en, kanunnik. Hij stichtte wiskunde-scholen en correspondeerde met veel geleerden. 24) Van Swinden zegt over deze ongelijkheid, p. 106 van zijn Verhandeling [over Huijgens als uitvinder der slinger-uurwerken] (No. 559, n.2), "namelijk die welke ontstaat door verandering van de temperatuur van de lucht. Dat deze waar is staat vast; maar Wendelinus had die veel groter geschat dan de juiste." [ Aanvulling, p. 635: Zie G. Wendelinus, Eclipses lunares, Antw. 1644, p. 25 (invloed amplitude). De ongelijkheid van Wendelinus wordt genoemd in Horologium (p. 13-14, zie T. 17, p. 70, n.1); voor zijn experimenten zie: P. Gassendi, Epistolae, T. 6, 1658, p. 457, 458, 493 — p. 497: zomer en winter; Mersenne, Cogitata, 1644, p. 369.] |
[ 305 ]
|
een wieltje aan zijn slinger gekoppeld om zijn slingeringen te tellen; maar met het zo inrichten van een Horologium hield hij zich niet bezig, wat u met uitstekend succes ten uitvoer hebt gebracht.
|
|
Wat de heer Wren in ons land over deze zaak heeft verzameld, uit wat door hemzelf en anderen is waargenomen, had ik gehoopt u al eerder te hebben meegedeeld, als de bescheidenheid van deze heer niet had gemaakt dat hij het zijne van minder belang vindt dan juist is. Toch heeft hij de verwachting gewekt dat u met deze brief iets daarvan zult ontvangen van hem. Doch als hij had gemeend dat de hypothese van Hodierna of van Hevelius kon voldoen aan alle verschijnselen van Saturnus, zou hij al vele jaren geleden in staat zijn geweest zulke of ook meer voorbeeldige hypotheses uit te geven. Wat nu die hypothese van u is volgens het juiste Anagram, hebben wij nog niet begrepen.
Aangezien u er nog naar vraagt, wat dat betekent in ons Anagram, quasi lunando vehitur 27), valt te vermoeden dat mijn brief die op 29 mei 1656 aan u is geschreven verloren is gegaan 28). Ik had in elk geval in die brief erop gewezen, dat ik met deze woorden alleen bedoelde dat de begeleider van Saturnus geheel op dezelfde manier om Saturnus draait als de Maan om de aarde, Namelijk, zoals de grote baan van de Aarde de hele kringloop van de Maan met zich meevoert, zo doet de baan van Saturnus het met de kringloop van zijn begeleider. Evenzo dat de begeleider van Saturnus, zoals de Maan van de Aarde, voorzover we tot nu toe hebben kunnen zien, de enige is, en niet zoals bij Jupiter een viertal; maar ook niet met het lichaam van Saturnus verbonden, zoals de hengseltjes. En dat ongetwijfeld, zoals de Maan haar fasen ten opzichte van de Aarde afwisselend verandert, de begeleider het zo doet ten opzichte van Saturnus (dit is tenminste geloofwaardig, al kunnen we dat wegens de afstand hier niet merken). Dit alles bedoelde ik met het woord Lunando (misschien een vreemd woord); waarvan echter de letterlijke betekenis of de vreemdheid verzacht leek te worden door het woordje quasi eraan te verbinden. Maar in dezelfde brief wees ik er ook op, dat noch ik, noch de heer Paul Neile of een ander van de onzen iets heeft willen afdoen aan de lof voor uw waarneming; maar dat u de lof krijgt voor die welke u als eerste aan de wereld hebt bekend gemaakt. Zodat u ook datgene wat ik had geschreven maar moet beschouwen als onder ons gezegd, en niet behoeft te vrezen dat het uw roem benadeelt; 25) Zie het werk van brief No. 360a, n.2 [Protei coelestis vertigines seu Saturni Systema, 1657]. 26) Zie het werk van brief No. 302, n.2 [Dissertatio de nativa Saturni facie, Gedani 1656. [ *) Divini zegt in zijn Brevis annotatio, 1660, T. 15, p. 407: "Digby ... heeft er zes meegenomen toen hij uit Rome vertrok".] 27) Zie brief No. 277. 28) De brief is inderdaad niet gevonden. |
[ 306 ]
|
wat ik herhaaldelijk weer zeg; en heus, het komt of kwam niet bij ons op, met u daarover te twisten. Maar indien u in uw verhandeling iets over deze zaak wilt opnemen, is het wel voldoende als u opneemt (wat ook waar is) dat de Engelse ridder Paul Neile, samen met de heer Wren, professor in de astronomie te Londen, an anderen, datzelfde sterretje in dezelfde tijd vrij vaak hebben gezien. Maar toch is er nog een ander verborgen mysterie, dat u misschien niet vermoedt. Dat zal ik u onthullen, als u belooft op mij niet boos te willen worden als ik zeg dat ik vriendschappelijk een spelletje met u gespeeld heb 29). Maar waarom zou ik stamelen? Ik geef me namens u deze verzekering: aangezien ik te maken heb met een eerlijke man, zullen eerlijke spelletjes hem ook niet mishagen. Dus krijgt u het. |
| Het uiteenzetten van mijn Anagram 30) is niet eerder gedaan dan toen ik uw uiteenzetting had ontvangen, waarmee ik het mijne met opzet in overeenstemming heb gebracht. Wat gedaan is, niet met de bedoeling u iets te kort te doen (ik heb namelijk ook niet aan iemand iets bekend gemaakt dat daarop betrekking heeft, als u althans uzelf uitzondert), maar om u proefondervindelijk te laten zien, hoe u niet absoluut veilig beschermd kunt zijn met uw enigma. En toen ik dan uw eerste bij mij neergelegde raadsel had ontvangen, werden steeds twee dingen in gedachten gehouden. |
| Het ene is, dat ik wist dat de heer Paul Neile samen met de heer Wren, al veel over Saturnus had waargenomen, wat door anderen nauwelijks eerder was waargenomen, naar ik meende; en uw brief 31) verschafte wel meer dan één handvat waarmee ik kon gissen dat dit raadsel over Saturnus moest gaan, en ik heb het inderdaad niet slecht gegist. En zo heb ik gedacht dat niemand onrecht aangedaan zou worden, als ik door middel van een dergelijk raadsel voor ieder zijn eer ten aanzien van de verschillende waargenomen fasen van Saturnus in goede staat zou houden. |
| Het andere was speels, namelijk om een beetje indruk op u te maken door te spelen (maar iets dat later uitgelegd zou moeten worden). Ik wist in elk geval (want vroeger heb ik anagrammen niet zonder succes gebruikt), dat de zaak niet geheel en al ongeloofwaardig was, dat zo goed als willekeurig geplaatste letters — althans als ervoor gezorgd wordt dat er van letters die vaker voorkomen meer worden geplaatst, en van de zeldzamere minder; waarmee ik vertrouwd was geraakt, en waarmee ik enige malen bezig ben geweest, door de frequentie in onderschepte brieven geschreven in cijferschrift, zoals men zegt — met opzet zó kunnen worden verplaatst, dat ze hoe dan ook een passende betekenis krijgen, en zelfs zodat ze op bijna elke willekeurige betekenis tenminste lijken neer te komen. En ofschoon u misschien zou zeggen dat hiervoor talent nodig is, u ziet hoe ik in dit geval geslaagd ben (misschien bent u ook verbaasd). |
|
Om dus beide tegelijk te bewerkstelligen, heb ik mijn enigma zó opgesteld dat ik aan de letters, die enige woorden uitdrukken voor de verschillende door de onzen kort daarvoor waargenomen fasen van Saturnus, andere heb toegevoegd waarvan ik niet wist wat ze zouden betekenen, maar waarmee ik erop vertrouwde dat ik later dat verborgene van uw enigma, wat het ook was, zou kunnen uitdrukken. Wat ook gebeurd is. En nu hebt u dan de zaak helemaal. Als u dat maar toevoegt, dat dit nieuwe sterretje door de onzen al vrij vaak eerder is gezien; maar ze hadden niet opgemerkt dat het een planeet is, voordat u erop gewezen hebt; deze eer gunnen wij u onverminderd.
29) Het is de sleutel van de mystificatie waarvan Chr. Huygens lange tijd de dupe is geweest. 30) Zie brief No. 227. 31) Zie brief No. 224. |
[ 307 ]
|
Wat ik meende u niet langer te moeten verhelen, daar ik begrijp dat u over deze zaken een verhaal voorbereidt; ik hoop dat die scherts van ons u echt geen onrecht aandoet. Onschuldige spelletjes zult u mij ondertussen kwijtschelden. De Problemen van een anonieme Fransman die u vermeldt over de Cycloïde, die ook hier zijn terecht gekomen, hebben we tenminste voor het grootste deel opgelost, zowel ik als ook de heer Wren; of ze echter alle anders kunnen worden opgelost dan meetkundig met benadering hebben we betwijfeld. Men zegt echter dat de oplossingen van alle sedert 1 oktober al door de bedenker in Frankrijk zijn gepubliceerd 32), welke dat nu zijn hoor ik nog niet. Doch als het (wat ik vermoed) 32) De stukken van brief No. 548, n.2 ['Réflexions sur les prix', 7 okt. 1658 (ed. 1779); 'Annotata in quasdam solutiones', 9 okt. 1658; 'Historia Trochoidis', 10 okt. 1658], en enkele van de volgende ... a) 'Récit de l'examen et du jugement des escrits envoyez pour les prix ...', Par. 25 nov. 1658. b) 'Historia Trochoidis sive Cycloidis Continuatio ... cujusdam viri machinamenti ...', 12 dec. 1658 (die persoon was Ant. de La Loubère). c) Lettres de A. Dettonville contenant quelques-unes de ses inventions de geometrie, Par. 1659. Hierin vindt men de volgende stukken: α) 'Lettre de A. Dettonville a Monsieur de Carcavy' ... β) 'Lettre de A. Dettonville a Monsieur Hugguens de Zulichem ...'. γ) 'Lettre de A. Dettonville a Monsieur de Sluze' ... δ) 'Lettre de A. Dettonville a Monsieur A.D.D.S.' ... (Arnauld docteur de Sorbonne). d) 'Lettre de Carcavy à M. de Dettonville', 10 dec, 1658, e) 'Traitté general de la Roulette' [W]. |
[ 308 ]
| Pascal is die dit heeft voorgelegd, aangezien diezelfde ook (wat ik eveneens verneem) intussen van alle anderen de oplossingen heeft beschouwd die zijn aangevoerd, hiertoe aangewezen door Carcavi naar hij beweert, weet ik niet hoe gezegd kan worden dat dit eerlijk gebeurt, daar het niet vrij is van alle verdenking dat hij daarvan voor zichzelf enige oplossingen of tenminste handvaten voor oplossingen heeft kunnen nemen. Zoals het ook niet eerlijk lijkt, dat ze enkele hiervan aanbieden, die al vroeger door Roberval opgelost zijn, en misschien voor een aantal vrienden (privé, denk ik) uiteengezet, en dat daarom iemand die dezelfde nu heeft opgelost geacht moet worden niets te hebben gevonden. |
|
Maar, zeg ik, mits hij die voor zich en de zijnen privé heeft gehouden en niet gepubliceerd, óf zij hadden deze zelfde problemen nu als bekend moeten uiteenzetten, en nu niet om te onderzoeken voor een prijs; óf degene die de zo voorgelegde problemen heeft opgelost zal niet minder moeten worden geacht iets te hebben gevonden, dan hij vroeger. Althans als die niet kan worden geacht op de een of andere manier het zijne te hebben ontleend aan de vondsten van Roberval (wat de Fransen nu opwerpen tegen Torricelli's gepubliceerde meting van de Cycloïde*), namelijk dat hij deze van Roberval geleerd heeft; hoe waar het is, weet ik niet). Maar dit, en andere dingen, laten we aan hun eerlijkheid over. Blijft over, dat ik tenslotte een punt zet achter deze uitvoerige brief; en dat ik, u voorspoed toewensend, afscheid neem.
[ *) Opera geometrica Evangelistae Torricellii, Flor. 1644, 'Appendix, De dimensione cycloidis'.]
|
[ T. I, 481 ]
|
J. Wallis aan Christiaan Huygens.[Aanhangsel bij No. 325.][ Verkeerd geplaatst.]*) Nu ik de brief ga verzegelen heb ik het een en ander toe te voegen. Het eerste is dat de heer Wren (die zoals meestal in Oxford verblijft, behalve dat hij op gezette tijden naar Londen wordt weggeroepen) hetgene dat ik van hem verwacht had om hierbij te zenden [<], nog niet heeft geschreven, maar hij belooft dit binnenkort te zullen doen. Het andere is over mijn op 29 mei 1656 aan u geschreven brief 1), die naar ik nu vermoed verloren is gegaan, wat ik ook zeer betreur; aangezien daar verschillende dingen in stonden waarvan ik niet wilde dat u er zo lang onkundig van zou blijven. |
| Ik had daarin namelijk (onder andere) uiteengezet wat die woorden willen zeggen [quasi lunando vehitur 2) (beweegt zich als met een maansikkel)] (maar dit is van weinig belang). Verder had ik ook besloten dat u gerust moest zijn over wat bij ons is waargenomen, als iets dat voor u niet schadelijk zou zijn om veilig de roem te verkrijgen die u verdiend hebt voor het waarnemen van de begeleider van Saturnus (wat ik had gedaan opdat de uitleg van ons anagram u niet zou verontrusten; en wel voornamelijk daarom betreur ik het verlies van die brief, omdat ik u dientengevolge misschien langer bezorgd heb gehouden dan ik wilde; ik had namelijk gemeend u na één of hoogstens twee maanden van deze vrees bevrijd te hebben). |
| Ook wees ik in diezelfde brief op de band van Saturnus die de heer Ball 3) vroeger al had waargenomen, en ik trachtte te weten te komen of u dezelfde gezien had (en ik verbaasde me er wel over daarop nog niets ten antwoord ontvangen te hebben). Ik vroeg eveneens, namens de heer Paul Neile, of u zo goed wilde zijn ons de maten aan te geven van de glazen van uw buiskijker, namelijk hoeveel, en welke, of ze alle bol waren of ook hol, eveneens welk gedeelte van een bol, en op welke afstand opgesteld; om de uwe en de zijne beter te kunnen vergelijken (maar ook hierover hebt u niets geantwoord). |
| Ik had ook iets toegevoegd over de fasen van Saturnus, zoals hier gezien; en bovendien de hoofdzaak van wat we ons hadden voorgesteld over zijn werkelijke vorm en beweging. Ik had gezegd dat vooral dit ons het meest in zorgen had gehouden bij het bepalen van de vorm en bewegingen van Saturnus, namelijk in hoeverre waarnemingen van anderen te vertrouwen zijn. |
|
Wij hadden ons in elk geval twee vormen van Saturnus voorgesteld. De ene eenvoudig, en zich beperkend tot één beweging; die ook verkieslijker lijkt, maar we hebben gezien dat als we deze aannemen er niet weinig door anderen vermelde waarnemingen verworpen moeten worden, althans verbeterd; wat we dus gemeend hebben niet zomaar te moeten doen, en niet dan nadat
*) [Volgens T. XV, p. 446, n.2 behoort dit stuk bij brief No. 560, van 1 jan. 1659.] 1) Deze brief is niet gevonden. 2) Woorden uit het anagram van Wallis. Zie brief No. 277 [<]. 3) William Ball [1627 - 1690] [^] bezocht de bijeenkomsten van Gresham College en werd de eerste treasurer van de Royal Society. Ball hield zich veel met Saturnus bezig. [Band: schaduw van de (onzichtbare) ring.] |
[ T. I, 482 ]
| de betrouwbaarheid van volgende waarnemingen dit noodzakelijk gemaakt zal hebben. Een andere — die ook (zoals meestal) zou beantwoorden aan verschijnselen door anderen vermeld, maar die de vorm van Saturnus nogal wanstaltig zou weergeven (en die niet zo gemakkelijk in een vlak te vertonen is) — die ook een tweevoudige beweging scheen te eisen, en wel om verbonden assen; als namelijk te oordelen is dat de waarnemingen van allen geheel te vertrouwen zijn. Maar als sommige ervan verworpen of verbeterd kunnen worden (wat van dag tot dag meer en meer noodzakelijk lijkt), lijkt die eenvoudiger vorm en enkelvoudige beweging te voldoen. |
Deze was nu als volgt; dat namelijk aan het bolvormige lichaam van Saturnus twee vlakke oortjes vastzitten (ongeveer van die vorm waarmee, bij ons althans, sommige hangsloten gezien worden, als er aan weerszijden oortjes waren), en wel zo:  ; en ze moeten bewegen om de lange as*); en daar komt het openen en sluiten van de oortjes vandaan. En ook zeer ten gunste van deze hypothese hadden we gezien dat gedurende enkele jaren de oortjes eerst open waren en langzamerhand dichtgingen, totdat het neerkwam op aan weerszijden uitgestrekte armen (waarmee nu ook een tegengestelde verbreding overeenstemt), en inderdaad, als alleen de rand van de oortjes naar ons oog toegewend is, dan zou die van een zo kleine dikte kunnen zijn dat hij verdwijnt, en dat alleen het bolvormige lichaam van Saturnus gezien wordt.
|
| Tenminste hierin schoot onze waarneming tekort, dat we niet de overgang opmerkten van de opvallende vorm met uitgestrekte armen naar de ronde vorm; of dit eigenlijk gebeurt door dunner te worden en tenslotte te verdwijnen, of dat het veroorzaakt is door verkorting; wat u misschien uit uw waarnemingen zult kunnen aanvullen. Als het dat eerste is geweest, zal een enkelvoudige beweging om de lange as volstaan (maar dan waren niet weinig waarnemingen te verbeteren). Maar als het andere het geval was, zal ook een beweging om de andere as toegestaan moeten worden, naar het schijnt. |
|
En de halve periode zal zijn wellicht veertien, of hoogstens vijftien jaar; maar binnen zeven of acht jaar zullen de afwisselingen van alle vormen zich vertonen; en we hebben gemeend deze tijd te moeten afwachten voordat er iets zekers is vast te stellen. Doch hoe dit alles met uw hypothese overeenkomt zal ik (als u althans gemeend hebt deze al te moeten onthullen) gaarne horen; en we hebben tot nu toe immers ook niets gehoord over de uitleg van uw enigma. Nogmaals: het ga u goed.
[ *) Deze figuur komt uit het origineel, UB Leiden (Codices Hugeniani). Vergelijk: A. van Helden, 'Annulo cingitur' (J.Hist.Astr. 1974, p. 159, 166) en 'Saturn' (Galileo project): figuur "Wren's theory". OC T. III, figuur bij p. 419-424; Engl..]
|
|
No 574.
Christiaan Huygens aan J. Wallis.31 januari 1659 (Concept).*)Aan Wallis. |
| 31 Jan. 1659. |
|
Brief van Meibom, niets over hem; en ik meen dat er hier niets beschikbaar is.
Over de Cissoide: het is meer dan ik gedacht had, evenwel voor de zekerheid van het bewijs moet men de oude manier prefereren. Dat ik ook twijfel of hij wel een stuk zou kunnen meten. Of Slusius aan hen daar niet over geschreven heeft, waarom ik het vermoed. Wie hij is°). Wat er tussen ons gepasseerd is dienaangaande, dat ik hem mijn manier van bewijzen gezonden heb 1), waarmee bewezen werd dat het stuk
[ *) Gedeeltelijk in het Nederlands geschreven.] [ °) In het origineel staat dit ingelast boven 'Slusius'. Wallis kende hem niet: p. 359 onderaan.] 1) Zie brief No. 487 [28 mei 1658, aan R. F. de Sluse; zie ook No. 483 hierboven]. |
[ 330 ]
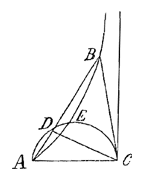AEBC het drievoudige is van het segment DEC, maar aangezien het lang is, heb ik geen zin het nog eens op te schrijven, daar ik nog meer te schrijven heb. Ik vind het lichaam uit het zwaartepunt net zoals hij, al lang geleden wist ik het. Dat als van 2 vlakke oppervlakken de verhouding gegeven is, en hun zwaartepunt ook, hun lichamen ten opzichte van elkaar bekend zijn. Zo ook als de lengte van een lijn en het zwaartepunt bekend zijn, dan is de oppervlakte die deze maakt bij het omdraaien bekend. Dit is mij nu nog kort geleden van pas gekomen bij de Cycloïde waarvan Wren de lengte gevonden heeft, en ik het zwaartepunt. Welke verhouding. Uit de Historia Trochoidis, opgesteld door Pascal en Roberval, heb ik Wrens vondst begrepen, die belangrijk geacht moet worden en me buitengewoon beviel. Het is het beste dat er van die lijn gevonden is. Want ik onderscheid de moeilijke van de elegante. Ik vond het bewijs en in het algemeen &c. Dit en hetgene dat ik nog meer daarvan gevonden heb, heb ik naar Frankrijk geschreven (?), waar nog geen oplossingen te voorschijn zijn gekomen, voorzover ik weet. |
| Ik heb ook toegevoegd mijn vondsten die ik een heel jaar geheim had gehouden, of in elk geval alleen afgestaan aan de een of ander, onder belofte van stilzwijgen. Doch nu heb ik besloten die bekend te maken opdat, terwijl overal buitengewone werken (?) [mannen?] voortgaan, wij niet gezien worden als geen bijdrage leverend. Daarom zal ik die dingen hier ook met u delen, en ik zal uiteenzetten wat ik over oppervlakken van Conoïden en Sferoïden als eerste, voorzover ik weet, heb gevonden.*) |
|
Ik vind het jammer dat Wren niets gezonden heeft; en ik hoop dat ze voor mij de hunne ook beschrijven. U hebt misschien van de Fransen iets van Conoïden. Mijn hypothese over [Saturnus].
[ *) Wallis geeft hiervan op 4 dec. 1659 een citaat uit de brief, zie hierna p. 519.] |
[ 331 ]
| Mijn verrekijkers, hoe ze zijn. Balthazar Conradus [<]. De brief van 29 mei 1656 is verloren gegaan 2). |
|
Anagrammen zijn veilig genoeg als ze kort zijn. Ik ben om de tuin geleid, beken ik, en ik heb zelfs niet vermoed dat er list in het spel was, en het is niet verbazend aangezien u die ook met ongewone subtiliteit hebt overdacht, maar anderen heb ik geloofd die iets gingen vermoeden, als ik zo*) vaak vroeg naar uw anagram dat wel lang was en naar die met moeite eraan ontwrongen betekenis. En het is nooit bij me opgekomen, waarom u mij 3) zou willen beetnemen of waarom u, of anderen van uw illustere mannen, het plan zou opvatten zich andermans roem toe te eigenen, daar u genoeg kunt uitblinken met die van u. Doch ik ben blij met zulke vondsten die nu werkelijk van u zijn, zoals ik altijd vermoed had dat ze waren, namelijk goed gemeend, en zonder misleidingen. Het ga u goed.
2) De brief van J. Wallis aan Chr. Huygens waarvan sprake is in brief No. 560 [p. 305]. [ *) Origineel: 'cum' onduidelijk; 'ideo' is msschien 'adeo'.] 3) Lat. "in me": 'in' moet weggelaten worden, het is bij vergissing niet doorgestreept.
|
[ 357 ]
|
No 592.
J. Wallis aan Christiaan Huygens.28 februari 1659.
|
| Oxoniae Febr. 18/28 1658/9 1).
|
|
Ik ben u werkelijk heel dankbaar, illustere heer, dat u (wat ik begrijp uit uw zeer aangename brief, vandaag ontvangen) zo gemoedelijk onze spelletjes hebt verdragen.
1) Pas in januari 1664 werd, volgens een edict van Karel II, het begin van het jaar naar 1 januari verschoven; daarvoor begon het burgerlijk jaar op 25 maart, en later volgde men in Engeland nog algemeen het oude stelsel. |
[ 358 ]
|
Ook al zijn ze niet met slechte bedoelingen geprobeerd, toch zou een lichtgeraakt iemand ze zeker minder verdragen. Doch dat u zich voor de eerste vinder hield, hebben we niet alleen (zoals u merkt) rustig aanschouwd (en zeker zou het voor mij heiligschennis zijn anders te doen, en ik had allang besloten dat u daarover geen zorgen mocht hebben, als de brief maar niet verloren was gegaan), maar ook sprak geen van de meer bekenden er zonder lof over. En wat ik toen als spel had gedaan: opdat het voor u niet nadelig zou kunnen zijn waren zeer weinigen het helemaal te weten gekomen, en het zijn diegenen van de vrienden die u voldoende gunstig gezind zijn, en die ook veel achting voor u hebben zoals u verdient. De aanwijzingen over de opstelling van de lenzen in uw kijkerbuizen die u ons hebt willen geven, zal ik bij de eerste gelegenheid aan de heer Neile bekendmaken; die ook zijn lenzen op geheel dezelfde manier opstelt, behalve dat hij de twee die bij het oog zijn niet aangrenzend heeft maar iets van elkaar af; en de openingen neemt hij nu eens wijder en dan weer nauwer, door ringen van karton te gebruiken naar gelang de zaak het verdraagt, overeenkomstig met het verschil van licht, zowel in de lucht als in het object. En hij heeft plat-bolle lenzen, zoals de uwe. Van uw hypothese over de hengseltjes van Saturnus had ik niet eerder gehoord hoe die was, dan ik nu uit uw brief begrijp. Wat echter des te minder verbazend is, zowel omdat de onzen (van de hele wereld gescheiden) met buitenlanders vrij zelden een briefwisseling zijn aangegaan, als omdat de Fransen (aan wie u het bekend gemaakt hebt) er niet zo aan gehecht lijken te zijn de vondsten van anderen te roemen, als die van henzelf. |
Ik verwerp uw hypothese geenszins, maar ik aanvaard deze als vrij waarschijnlijk (waarvan het voornaamste punt wel wordt gesteund door de omloop van de Begeleider). Doch waarom wij meer overhelden tot de andere, komt vooral door het feit, dat door sommigen geleverde fasen hengseltjes hebben laten zien die wijder zijn dan het lichaam van Saturnus zelf (ongeveer met deze vorm)
welke verschijning zeker, als ze waar is, door deze hypothese niet wordt toegelaten. Maar ook al hebben we eraan getwijfeld, toch hebben we niet gevonden dat ze overhaast verworpen moest worden, totdat de tijd weer is gekomen dat diezelfde verschijning opnieuw (als ze waar is) te verwachten is. Wat de heer Wren betreft (die nu in Londen 2) woont): van zijn gissing hebt u de hoofdzaak in mijn brief ontvangen (als ik me niet vergis). Hij werd, zoals wij allen, in beslag genomen door de verscheidenheid van de fasen door verscheidene mensen geleverd. En hij is er nu mee bezig, om gezichtsbedrog van Telescopen te ontdekken, en door welke fouten anderen misleid kunnen zijn zodat ze die vormen hebben geleverd. Dit werk zal, als hij het afmaakt (wat ik hoop dat zal gebeuren), niet zonder nut zijn naar ik meen. Hoewel (om maar te bekennen wat waar is) deze man met een zeer scherp verstand zozeer te bescheiden is, en onbillijk met zijn vondsten, dat we het zeer moeilijk aan hem kunnen ontwringen dat hij in orde brengt wat hij heeft bereikt; maar hij heeft ook een vruchtbaar verstand, steeds zinnend op nieuwe dingen verwaarloost hij de vorige, en hij vindt ze het niet waard ze aan het licht te brengen. De fase van Saturnus vertoont zich aan ons geheel hetzelfde, gezien met langere kijkers, als ook aan u; maar met kortere lijkt hij ook nu bolletjes te hebben aan de buitenkant van de hengsels. Wat voor ons de zaak buiten twijfel stelt, dat de verschijningen van zulke bolletjes, al eerder door velen geleverd, bedrieglijk zijn geweest. Over de Cissoïde-lijn had ik niets bedacht voordat ik uw brief ontving; maar om 2) Sinds 1657 was Chr. Wren professor in de astronomie aan het Gresham College te Londen, hij werd pas in 1660 benoemd te Oxford. Zie brief No. 280, n.2. |
[ 359 ]
|
aan uw verzoek te voldoen heb ik na ontvangst van de brief terstond Pappus ingezien die beschikbaar was, om te zien wat hij over die zaak had geleverd (Eutocius 3) was namelijk niet bij de hand, ik heb hem dus niet geraadpleegd), opdat ik niet zou doen wat al gedaan was. En daarna heb ik de draad opgenomen van wat we hebben geleverd in onze Arithmetica infinitorum, met de directe methode heb ik in weinig uren beschreven wat ik nu had ontvangen. In elk geval had ik niets anders eerder of later over dit onderwerp zelf overdacht of van anderen ontvangen; als u tenminste uitzondert dat, toen ik de brief aan u ging verzegelen, waarbij ik hem aan de heer Wren heb laten lezen, deze heeft gezegd dat hij het laatste deel van uw propositie wel al eerder had gevonden, maar niet had opgemerkt dat die lijn de Cissoïde was geweest. Hij wees ook op hetzelfde, waar u nu op wijst, uit de Centrobarica 4) van Guldin; maar aangezien ik dat boek (ik beken het) niet gelezen heb, wist ik niet dat er iets van dien aard bij hem of bij iemand anders voorhanden was. Maar ik weet nog niet of hij dit algemeen heeft geleverd, of (wat de heer Wren aangaf, als ik me goed herinner) dat hij het met enige voorbeelden aanduidt zonder bewijs. Dat u nog twijfelt bij een deel van het oppervlak van de Cissoïde, of onze methode zo ver reikt dat ze de grootte daarvan ter beschikking stelt: ik beken dat mijn verhaal op dit punt enigszins verminkt is. Ofschoon ik namelijk de theorie volledig genoeg lijk te hebben gegeven, over zowel het onderling vermenigvuligenn als delen van directe reeksen, zowel oneindige als ook eindige (dat wil zeggen bij gegeven delen van de oneindige), hebben we daar toch karig gehandeld met het vermenigvuldigen van directe reeksen met omgekeerde reeksen, of delen erdoor. U zult zien dat dit echter gemakkelijk kan worden aangevuld voor wat betreft de oneindige reeksen, uit het voorbeeld dat u hebt ontvangen in mijn laatste brief aan u [<]. En zeker voor wat betreft de eindige reeksen, mits het niet een reeks is van universele wortels, kan ditzelfde met hetzelfde gemak worden gedaan. |
| Maar voor wat betreft eindige reeksen van Universele Wortels*) of Tweetermen of Resten, hoe dat gaat wordt niet geleerd. Om te laten zien wat er namelijk aan de hand is, toen ik dat boek uitgaf en de zaak gebracht had tot waar u ziet, heb ik besloten, deels omdat ik een beetje genoeg had van die bezigheid, deels omdat ik door andere geroepen werd, voor die tijd af te zien van verder onderzoek; en sinds die tijd heb ik tot nu toe zelfs geen tijd gehad om het weer op te pakken; zodat ik zelfs niet heb geprobeerd tot waar het verder uitgebreid kan worden. |
|
Maar ondertussen, wanneer we, ikzelf of iemand anders die serieus zijn aandacht hierop wil richten, het ooit opnieuw proberen, heb ik er alle vertrouwen in dat het niet zonder succes zal blijven. En niet zelden heb ik wel ondervonden dat de zaak ook in dergelijke gevallen geslaagd is; al ben ik nog niet begonnen aan het algemene verhaal ervan. Of het in dit geval zal lukken weet ik niet; en toch geef ik de hoop niet op; maar ik heb geen tijd (barstensvol met verschillende dingen) om het nu te onderzoeken; daarna kan het misschien gedaan worden zodra er tijd vrijkomt. De heer Slusius die u noemt ken ik niet, en ik herinner me niet hiervoor over hem te hebben gehoord. Maar ook niet uw heer Hudde, over wiens Methode van minima en maxima 3) Eutocius Ascalonita (6e eeuw) was commentator van Apollonius, in een editie van zijn Conica. Zie brief No. 5, n.4. [Apollonii Pergaei Conicorum libri quattuor, ed. Commandino, Bon. 1566.] 4) Zie brief No. 101, n.3. [ *) Een 'radix universalis' is √(... de wortel van wat volgt). Zie J. Sesiano, An Introduction to the History of Algebra (2009), p. 123 en ook J.J. Stampioen, Algebra (1639), p. 16.] |
[ 360 ]
|
de heer van Schooten ergens melding maakt; en hoe die methode is zou ik graag horen; ik geloof namelijk dat daarover nog niets in druk verschenen is 5); het heeft mij tenminste niet bereikt. De lengte van de Trochoïde-lijn, zowel voor wat betreft de gehele, als voor wat betreft de delen die de heer Wren heeft geleverd: namelijk dat een segment van de halve trochoïde-lijn begonnen bij de top, afgesneden door een rechte evenwijdig met de basis, het dubbele is van de koorde van de overeenkomstige boog van de voortbrengende cirkel, tussen de top en dezelfde rechte. Maar ook andere heeft hij (als ik me niet vergis) aan Carcavi gestuurd, die de schrijvers van de Historia Trochoidis liever zouden willen verzwijgen dan openlijk erkennen (zoals ook alles van mij); hoe die allemaal zijn weet ik niet, in elk geval had hij besloten mij slechts spaarzaam erover in te lichten, aangezien elk van ons met hetzelfde onderzoek bezig was. En wat ik zelf tot stand heb gebracht, zult u misschien binnenkort uitgebreid horen, wanneer ik de tijd gekregen heb dat in orde te brengen. |
|
Ondertussen begrijp ik dat die verhouding die u levert, van het oppervlak beschreven door de Trochoïde-kromme gewenteld om de basis, tot de voortbrengende cirkel, namelijk van 64 tot 3*), geheel en al waar is. Die is in elk geval gelijk aan die van de Parabool waarvan de basis is viermaal de diameter van de voortbrengende cirkel, de hoogte tweemaal de omtrek daarvan; en de respectievelijke delen ten opzichte van elkaar genomen. En een ander omwentelingsoppervlak van de halve trochoïde, genomen om de as, is gelijk aan twee vierkanten van de omtrek (of, als u liver wilt, aan een rechte hieraan gelijk) min 32/3 van de oppervlakte van de voortbrengende cirkel. En de delen ten opzichte van delen van een zekere vlakke figuur die geen naam heeft, maar waarvan we de afmeting bedoelen. Maar over deze en andere dingen later meer. De oplossingen van Pascal [<] zijn nog niet bij u gekomen, begrijp ik, zoals ook niet bij ons. Waaruit ik opmaak dat hun openbaar maken met een bijzondere betekenis moet worden opgevat. Namelijk het feit dat een van hen het tegen een ander heeft gezegd, dat dit voor geopenbaard te houden is, zodat als iemand anders van de stervelingen ditzelfde heeft gevonden hij toch niet als de uitvinder beschouwd moet worden,; terwijl ze het ondertussen, als niet anderen het gevonden hebben, niet te weten zullen komen van hen. Bij uw overige zeer welkome proposities die u bijvoegt, heb ik niets anders dan mijn dank in plaats van de uwe te stellen. In elk geval heb ik nu de tijd niet om ze geheel te beoordelen, en ook niet (geloof ik) dan nadat er enige tijd vrij zal komen. Aangezien ik echter zie dat enige bezigheden mij van huis wegroepen, wilde ik liever in elk geval dit inderhaast schrijven, dan elk antwoord op uw brief uitstellen. Het ga u goed, weledele heer, en blijf houden van |
Amantissimum pariter atque observantisimum Tui Johannem Wallis. |
| Clarissimo Nobilissimoque Viro, D. Christiano Hugenio, Constantini filio, tradantur Hagae-Comitis.
| ||
1 
| Leave it at ye forraign post-house in London to bee sent to the Hague in Holland. | |
|
5) In Geometria Renati Descartes opera Fr. a Schooten, 1659 (2e ed.), p. 401-506 en 507-516:
|
|
No 625.
Christiaan Huygens aan J. Wallis.9 juni 1659 (Concept).*)
|
| 9 Jun. 1659. |
| Wallis. |
Dat ik deze gelegenheid aan hem te schrijven lang verwacht heb, 3 maanden a). Dat ik deze exemplaren weinige dagen geleden 1) gekregen heb, het mijne wat eerder 2). Dat er een brief van Carcavi 3) bij is, maar oud, waarmee hij mij verzoekt deze 4 4) naar Engeland te zenden; en hij zou zelf geschreven hebben maar was niet wel. Verzoekt mij zijn excuses te doen en vertrouwt dat u die zult willen bestellen, ook aan Hobbes, alhoewel hij u geen vriend is. Verzoekt UE. en hun aller oordeel. Ik verlang er ook naar, en of u ook iets uitgeven zult daarover. |
| Wat mij betreft is het de zeer grote subtiliteit in die aan Carcavi 5) die ik bewonder en heel waardevol vind. De moeilijkheid is heel groot, maar er zijn andere waarbij we subtiliteit en vernuft kunnen aanwenden, die gaan over dingen die aangenamer zijn om te weten. Over de vergelijking van cycloïde-lijnen met ellipsen; ze lijken elegant, daarvoor heeft echter de heer Wren de gelegenheid verschaft met zijn vondst. |
|
Hier kan ik niet nalaten u op de hoogte te stellen van een uitstekende vondst van onze Heuraet, ik weet niet of u deze naam hebt gezien in brieven van van Schooten. Toen hij had vernomen dat ik het oppervlak van een Parabolische Conoïde had gemeten en een rechte lijn gevonden gelijk aan een parabool met verondersteld de kwadratuur van de hyperbool (waarover ik u vroeger heb geschreven), heeft hij niet alleen beide hiervan op eigen houtje gevonden, maar ook heeft hij rechten getoond die absoluut gelijk zijn aan andere krommen, van de soort die we in de Meetkunde hebben opgenomen. De eerste ervan en ook de eenvoudigste is deze ABC, waarbij de derde machten
[ *) Gedeeltelijk in het Nederlands geschreven.] a) Wallis. Wardo. Wren. Hobbes. Of hij wat gereet maeckt. [Huygens.] 1) Op 5 juni. Zie brief No. 622 [daarin genoemd: Lettres de A. Dettonville]. 2) Begin mei. Zie brief No. 615. 3) Zie brief No. 594 [van 7 maart 1659]. 4) De vier personen worden genoemd in noot a. 5) Dat is de brief van A. Dettonville aan P. de Carcavy, zie brief No. 560, n.32. |
[ 417 ]
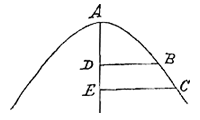van de op de ordinaat gezette CE en BD onderling die verhouding hebben welke de kwadraten van de onderschepte EA en DA hebben. Deze lijn is eerder beschouwd door Meetkundigen en ze hebben de kwadratuur van het oppervlak gegeven; maar er dat een rechte is, gelijk aan een willekeurig gedeelte ervan, heeft tot nu toe niemand opgemerkt. Deze vondst, kort uiteengezet door de bedenker, heeft van Schooten toegevoegd aan de nieuwe uitgave 6), die nu is verschenen, van de Geometria van Descartes, waarin u deze zult vinden 7), en ook andere dingen dan wat door Heuraet scherpzinnig is gevonden. U zult eveneens zien die methode van Hudde 8) voor het bepalen van een maximum of minimum, die we echter bij een lichaam niet aan hem te danken hebben, maar de eerste vinding ervan veeleer aan Fermat. Diens methode had ik namelijk ook al eerder tot deze zelfde bekorting gebracht als die Hudde gebruikt, en de hele grondslag ervan had ik, duidelijker dan door hem is gedaan, in een geschrift uitgelegd ter wille van de heer de Witt, pensionaris van Holland. Het nut ervan is verreweg het grootst bij het vinden van raaklijnen aan krommen.
|
|
In het tweede deel van de Geometria van Descartes, dat nog niet gedrukt is, zullen zowel enkele andere dingen staan, als twee werkjes 9) van de genoemde heer de Witt, het ene over kegelsneden, het andere over vlakke en vaste plaatsen. Ik meen dat geen eeuw even rijk is geweest aan Meetkundigen, onder wie deze man, als hij zijn bezigheden minder zou verdelen, wel de voornaamste plaats zou kunnen krijgen. Mijn Systema Saturnium zal ik u binnenkort toesturen, er zijn namelijk nog enige bladzijden die door de drukker moeten worden gedrukt 10). Hoe de onderneming slaagt voor hen die in Oxford ervoor zorgen dat Uurwerken volgens onze uitvinding worden gemaakt, zou ik willen weten 11). Ik heb er één waarvan de slinger drie voet is.
6) Zie brief No. 306, n.3 [Geometria, 1659, p. 517-520]. 7) Zie over dit artikel van H. van Heuraet brief No. 587, n.5. 8) Zie brief No. 592, n.5. 9) Zie brief No. 597, n.1 [Joh. de Witt, Elementa curvarum linearum, Liber primus, secundus]. 10) Toegevoegd: excudendae supersunt [Apographa]. 11) Toegevoegd: scire velim [Apographa].
|
[ 518 ]
|
No 690.
J. Wallis aan Christiaan Huygens.4 december 1659. 1)
|
| Oxonijs. Novembris 24. 1659.
|
|
Op uw brief (weledele heer) gedateerd op 9 juni 2), had ik het antwoord allang gereed gemaakt, maar aangezien het lang was, en zeker van dien aard dat het vrij goed paste bij de Verhandeling die ik onder de pers had over de Cycloïde 3), heb ik besloten het hieraan toe te voegen; en ik heb gedacht dat het u om deze reden niet minder
1) Chr. Huygens ontving deze brief pas op 10 [20] maart 1660, zoals blijkt uit de brief [No. 736] van 31 maart 1660 2) Zie brief No. 625. 3) J. Wallis, Tractatus duo. Prior, de cycloide ... Posterior, epistolaris ... de cissoide ... de curvarum ..., Oxon. ... 1659. De brief 'Nobilissimo ... Christiano Hugenio Const. F., Johannes Wallis S.' vormt het 2e deel, op p. 75-123 [beginnend (t/m p. 81, Ned. hierna) met het antwoord op Huygens' brief van 9 juni]. Herdruk: Opera, 1695, I, p. 542-569. |
[ 519 ]
|
welkom zou zijn, ook al zult u het wat later hebben ontvangen. Het zou echter niet tot nu toe zijn uitgesteld, als niet ondervonden was dat vertragingen bij de pers groter zijn dan ik gehoopt had. Hoe het ook zij, ik hoop dat u het voor lief zult nemen. Doch ik wil u verder niet tot last zijn, door hier te herhalen wat daarin te vinden is. Dit ene leek mij toch iets om op te merken, namelijk: óf ik volg uw gedachte niet goed genoeg, of er is in datgene wat in uw eerdere brief (gedateerd op de laatste van januari 1659 4)) beschreven moest worden, iets fout gegaan. Toen ik namelijk het oppervlak van een Parabolische Conoïde op mijn manier onderzocht, en daarna mijn regel met de uwe vergeleek, bevond ik dat de uwe (als ik het goed begrijp) noch met onze regel, noch ook met uw getallen overeenkomt; wat maakt dat ik een fout bij het overschrijven vermoed. Het staat er in elk geval als volgt 5):
Maar ik zeg: als AD = DC = CA = 6, zal gelden zoals AD + DC + CA =18, tot AC = 6, zo is AC tot E = 2. Dus AD + DC + E = 14, tot 2/3 AC = 4, zoals 14 tot 4; niet zoals 14 tot 9. Wat we over de Cycloïde hebben verschaft, als u het gezien hebt zult u er geen bezwaar tegen hebben, hoop ik, het vrijmoedig met mij te behandelen als u iets vindt dat anders is dan het zou moeten zijn. Maar als u met mij vindt, dat Pascal en de overige Fransen teveel gehecht zijn aan hun werk dan dat ze het aan buitenlanders zouden aanbieden, zult u niet afkeuren 4) Zie brief No. 574, van 31 jan. 1659 [<]. 5) We vinden hier een deel van brief No. 625 [of 574?] waarvan we alleen het concept hebben. 6) Zie het stuk No. 678, met het theorema in exacte vorm [met: opp. kegel tot opp. conoïde]. [ *) Zie de eerste zin van het P.S. op p. 520.] |
[ 520 ]
|
geloof ik, wat we ter verdediging van Torricelli hebben geschreven [>]. Waarvan ik hoop dat, als het althans Roberval niet mishaagt, er niets in gevonden gaat worden dat iemand mij terecht kwalijk kan nemen. U die de man beter kent dan ik, misschien hebt u gemerkt dat hij wat moeilijker is bij vondsten van anderen, en gunstiger bij de zijne. Sommigen klagen erover, weet ik, dat hij nogal geneigd is bij anderen diefstal te vermoeden, en te beweren dat hem al eerder bekend was wat anderen naar voren brengen, terwijl hij ondertussen niets publiceert tot nut van het algemeen. Hoe het ook zij, ik ben niet afgunstig op zijn vindingen, en hij moet ook niet afgunstig zijn op werken van anderen. En als iemand anders hetzelfde vindt als hij, als hij zelf niet de zijne wil uitgeven, moet hij tenminse dulden dat zij hun vondsten ongestraft openbaar maken; tenzij hij wil dat ze niet tot nut van het algemeen zijn gevonden, maar tot nadeel van het algemeen. Maar dit tot zover. U zult mij intussen vergeven, hoop ik, als ik vrijmoediger met u spreek, dan ik gewend ben met iedereen. Wat uw Uurwerk betreft, dat hebben bij de onzen sommigen op de ene, anderen op een andere manier gewijzigd; echter zo dat de lof voor de onderneming bij u blijft. Onder anderen heb ik er gezien die van uw figuur het rad met zaagtandjes L 7) en dan ook het gevleugelde staafje MN, evenwijdig met de horizon plaatsen, en aan die verlengde MN de slinger hangen; maar sommigen passen ook andere veranderingen toe die niet zo gemakkelijk met woorden zijn uit te leggen. Uw Systema Saturnium heb ik wel gezien (bij de onzen is het in elk geval beshikbaar) en ik keur het goed; maar daarvan heb ik onlangs niets van u ontvangen. Wat ik vermeld opdat er niet een van uw brieven verloren zou gaan (wat ik niet zou willen). Verder, het ga u goed, weledele heer, en blijf houden van |
Tui observantissimum et amantissimum Johannem Wallis. |
Nadat ik het bovenstaande had geschreven, merkte ik op, dat de fout in uw Regel was, dat u twee derde 2/3, in plaats van anderhalf 3/2 hebt gezet. Als dit verbeterd wordt is het voor het overige goed. Ik heb onlangs een waarneming gezien van de heer William Ball, die op 12 november en volgende dagen de band van Saturnus heeft getekend die door het midden van het lichaam gaat, ongeveer op eenzelfde lijn als de lengte van de hengseltjes. Als dit van uw waarnemingen verschilt, moet worden bezien of het komt door een verschil van de kijkers, of door iets anders.
De heer Paul Neile (die u ook laat groeten) vraagt evenzo of u hem wilt kenbaar maken: 7) Zie de figuur tegenover p. 254. [ Wallis beschrijft de eerste constructie van het uurwerk (Coster, 1657), zie T. 17, p. 27, n.1 en fig. 3, 4.] |
[ 521 ]
u doet wanner u  en  waarneemt [Venus en Mercurius]; tenminste wanneer u de diameters meet. Anders zal immers moeten worden geschat dat de diameter van  kleiner is dan u er aan hebt toegekend. 3o. Of de twee glazen het dichtst bij het oog onderling aangrenzend zijn; of zo niet, door een hoe grote tussenruimte gescheiden. Twee exemplaren van het hierboven vermelde boekje zal de heer Samuel Thomson 8), boekhandelaar te Londen, sturen naar de heer Brown 9), boekhandelaar bij de uwen, om aan u te leveren; ik verzoek u ervoor te zorgen dat het andere aan de heer van Schooten wordt gestuurd, met de aan hem geschreven brief.
8) Samuel Thomson was toen boekhandelaar te Londen aan St. Paul's Churchyard. 9) Samuel Broun. Zie brief No. 307, n.1 [zie ook No. 731, n.8].
|
[ 75 ]
|
Nobilissimo Doctissimoque Viro,
D. Christiano Hugenio Const. F. |
TErwijl dit wat u hierbij zult ontvangen, weledele heer, een langdurig oponthoud bij de pers afwachtte, ontving ik na ongeveer een maand uw brief gedateerd op 9 juni. Die deels in herinnering brengt mijn eerder gedane beloften, u dit mee te delen; deels gaat over enige boeken uitgegeven door Dettonville*) oftewel Pascal, die de illustere Carcavi had gestuurd om uit te delen, en die naar hier gezonden moesten worden; zodra ik ze had ontvangen heb ik ze dadelijk uitgedeeld, met een beleefde groet van Carcavi, zoals opgedragen.
|
| De verhandeling van Dettonville. |
|
Wat betreft het nakomen van mijn belofte, met deze geschriften ziet u dit vervuld. De verhandeling van Dettonville (waarover u ook mijn mening vraagt, hetzij uit uw naam hetzij ook die van Carcavi) heb ik niet alleen gretig onvangen, maar ook dezelfde en de volgende dag bestudeerd; en ik vind deze vol scherpzinnigheid. En ik vloog er doorheen, met des te minder hindernissen of struikelblokken, omdat ik bevond dat hij in het geheel niet van mening verschilt met ons, en een niet zeer ongelijke methode neemt; wat u, nadat u de zijne met die van ons hebt vergeleken, snel zult vatten. Aangezien nu de geleerde heer al lang over deze zaak heeft nagedacht (die de Fransen al twintig of ook veertig jaar heeft beziggehouden) en hij zelf die problemen heeft voorgelegd [<] (of ze toen al door hem volkomen doorzien waren of niet, staat voor mij nog niet vast; *) Lettres de A. Dettonville contenant quelques-unes de ses inventions de geometrie, Par. 1659 (T.p.: ex. UCM). |
[ 76 ]
|
maar ik denk dat het onbetwijfelbaar is dat tenminste een groot deel ervan al door hem doorzien was), en de gelegenheid kreeg de geschriften van allen en waarvandaan
ook sinds die tijd hierover geschreven, en met deze aanleiding naar de heer Carcavi gestuurd (zoals verlangd werd) te bestuderen, en daaruit over te nemen wat hij tot het zijne wilde maken, of althans niet onbelangrijke handvaten aan te grijpen om zijn meningen te vervolmaken; daarom ontken ik niet, dat er misschien met veel meer zorg gemaakte dingen van hem te verwachten zijn, dan van mij, die dit zonder anderen en onervaren heb ondernomen. Behalve namelijk wat bij Torricelli voorhanden is [<], en bij van Schooten in zijn aantekeningen bij Descartes (ik weet niet of er ook bij Tacquet iets staat) herinner ik me niet, vóór de uiteenzetting van deze problemen iets over de Cycloïde gelezen of bedacht te hebben. Maar intussen schaam ik me er niet voor, bekend te maken wat ook ons in deze zaak ten deel is gevallen, en het zal degenen die hierin deskundig zijn niet mishagen (hoop ik). Maar aan de zeer geleerde heer moet verzocht worden ons niet te willen beschuldigen van diefstal (wat ik over Torricelli geïnsinueerd zie; hoe terecht weet ik niet, het is tenminste een beetje oneerlijk, nadat hij zoveel jaar geleden is overleden) als toevallig bij hem en bij ons niet zelden hetzelfde is opgekomen (vooral aangezien hij dat van mij eerder gezien heeft dan ik dat van hem); en ook dat hij niet wil dat van onze vondsten iets afgedaan gaat worden, als enige dingen hiervan toevallig door hemzelf of door Roberval (die ik voor een verbonden persoon houd) eerder is gevonden. Zolang zij immers hun vondsten voor zichzelf houden, en niet openbaar maken, zou het geheel en al onbillijk zijn als ze niet verdragen dat ook anderen die dingen vinden die ze zelf geheim houden, en intussen ook de roem van het vinden (als er enige is) wegdragen. |
| Als namelijk bijvoorbeeld (onder andere) ons wordt voorgesteld iets te onderzoeken (en wel voor een prijs) dat lastig is en vol moeilijkheden en dat bezoldiging verdient: Hoeveel is de grootte van het lichaam dat ontstaat uit omwenteling van een Cycloïde om de basis; dan moest het voor ons of onze naam niet nadelig zijn, als Roberval ooit (misschien enige jaren geleden) buiten ons weten dit ook heeft gevonden. En ook, als zowel ik als anderen ditzelfde op eigen houtje vinden (en we intussen niet elkaar diefstal ten laste leggen), moet daarom niet minder gemeend worden dat wij het hebben gevonden, dan Roberval zelf (niets verhindert immers dat hetzelfde wordt gevonden door verschillende mensen op hetzelfde open veld in de natuur). Als zij deze lof voor het vinden wel weggenomen willen hebben, was het behoorlijk geweest ons dit te laten zien als reeds gevonden, niet het voor te leggen als iets dat nu onderzocht moet worden. Wat ook tegelijk gezegd zij over andere vondsten van beide zijden. |
[ 77 ]
| En ik had wel liever gewild*), vooral om deze reden, dat de schrijver van de Histoire de la Roulette zich had ingehouden, tenminste bij wat tegen Torricelli is gezegd (tegen Torricelli, zeg ik; want over Laloubère°) ben ik minder bezorgd, als iemand die nog aanwezig is voor zijn verdediging), dan dat hij de zeer verdienstelijke man, nu al vele jaren geleden overleden, zou hebben beschimpt. We weten in elk geval uit zijn geschriften dat Torricelli zowel een geleerd man en Wiskundige was, als zich in de Wiskunde zeer verdienstelijk heeft gemaakt; ik geloof dat hij ook oprecht was. En ik zie bij hem niet iets verkeerds gedaan, dat bij de geleerde heer, of ook bij Roberval, voor wie hij partij kiest, wrevel zou kunnen wekken. |
| Torricelli heeft in het jaar 1644 onder andere uitgegeven zijn bewijzen over het Cycloïde-oppervlak als drievoudige van de voortbrengende cirkel [<]; maar waarom hij dit niet had mogen doen, zie ik niet. Dat die bewijzen van hem zijn, ontkennen ze niet; en ook geven ze niet als reden op dat hij iets van Roberval als het zijne heeft verkocht. Hij heeft zeker niet gezegd (hij wist het immers niet, ook als ze het zelf zeiden), maar hij heeft ook niet ontkend, dat Roberval dit ook had bewezen. Wat toen al óf algemeen bekend was, of niet. Als het wel zo was, kan dit niet onrechtvaardig zijn voor Roberval, als een ander na hem hetzelfde probleem oplost, niet meer dan voor Archimedes dat Torricelli na hem dezelfde kwadratuur van de parabool heeft bewezen. Als het niet zo was, zal men niet boos moeten worden op Torricelli omdat hij niet wist dat Roberval iets in zijn boekenkast voor zichzelf had gehouden, of ook aan zijn vrienden meegedeeld. Wij zijn tenminste meer verschuldigd aan Torricelli, die zijn bewijzen al in het openbaar bekend heeft gemaakt, dan aan Roberval, die de zijne nog altijd achterhoudt. En we oordelen dat het wel heel onbillijk is dat, als Roberval de zijne niet in druk wil geven, Torricelli dan ook niet de zijne mag geven. |
|
Maar, zeggen zij [p. 3], Torricelli schrijft aan Galileï toe, wat aan Mersenne, en aan zichzelf wat aan Roberval te danken is. Maar neemt u mij niet kwalijk, ik zie toch geen van beide. In elk geval was Roberval de bedenker van zijn oplossingen, en Torricelli niet minder van de zijne. Maar indien Roberval heeft gemeend dat het in zijn belang was dat de wereld zou weten dat de zijne de eerste waren, al wist Torricelli dit niet, stond het hem vrij dit bekend te maken, en hiervoor was het niet nodig Torricelli te beschimpen, die het niet wist, of hem te belasteren met ongerechtvaardigde verdachtmakingen. En het is er wel ver van verwijderd dat hij, ten nadele van Roberval, heeft beweerd dat hij de oplossing van dit probleem als eerste heeft gevonden, zo ver, dat hij zelfs niet zegt dat hij deze gevonden heeft. Maar alleen, na de waarheid van de propositie te hebben erkend, bevestigt hij die met bewijzen. En waarom dit niet ongestraft zou kunnen, zie ik niet.
*) Het volgende (t/m p. 78) wordt geciteerd in C. R. Dati, 'Lettera a Filaleti di Timauro Antiate Della Vera Storia della Cicloide', Fir. 1663, p. 6-7. °) Antonio Lalovera, De Cycloide, 1658; Propositio trigesima sexta, excerpta ex quarto libro de Cycloide Antonii Laloverae nondum quidem edito, 1659. Cf. Dominique Descotes, Blaise Pascal, littérature et géométrie (2001), p. 30-31. |
[ 78 ]
| Maar het zou kunnen zijn, dat hij tussen de papieren van Galileï het geschrift van Beaugrand heeft gezien, waarin deze een bewijs van Roberval, zonder de naam te noemen, naar Galileï had gestuurd; waaraan hij een handvat ontleend kan hebben voor die van hem. Dit vermoeden zij namelijk. Doch of ze dit voor zeker houden is mij onbekend; en ook niet of hij dit zelf heeft erkend, wat ze niet bevestigen, ze delen niet mee op grond waarvan het voor hen kan vaststaan. Maar hoe het ook zij, ze beschuldigen hem er niet van daaruit ontfutselde bewijzen voor de zijne te hebben verkocht, en ze ontkennen niet dat die welke hij aanvoert van hem zijn. |
| Wat het nu is, van welk vergrijp ze hem beschuldigen, begrijp ik in het geheel niet, en behalve slinkse verdenkingen voeren ze niet iets aan waarmee het kan vaststaan. Ja zelfs, zeggen ze (wat bij hen een voortreffelijk argument is) dat ze een brief van zijn hand hebben, die ze als een kleinood bewaren tot op deze dag (alsof de zaak wel van zo groot belang was), waarin hij aan Roberval de hoofdrol gunt bij het oplossen van dit Probleem. Toen de oprechte man tenslotte vernam wat hij niet wist terwijl hij het boek uitgaf, dat Roberval ook (buiten zijn weten) ditzelfde had bewezen, al had hij het niet in druk bekend gemaakt (wat hij nog steeds niet heeft gedaan, geloof ik), heeft hij dat zonder moeite erkend. Maar ze zeggen niet dat hij heeft te kennen gegeven, dat dit hem onbekend was toen hij het boek uitgaf, en ze beweren het ook niet zelf; zelfs leren ze het tegendeel. |
| Daarom weet ik niet wat zij afkeuren, tenzij ze willen dat het ongeoorloofd is, dat iemand anders vindt, of openbaar uitgeeft, wat misschien buiten zijn weten Roberval voor zichzelf houdt, of liever alleen aan de zijnen bekend wil hebben. Wat echter Mersenne betreft, aan wie ontzegd wordt, naar ze aanduiden, wat aan Galileï wordt toegeschreven: mijns inziens berust dat zelfs op geen enkele, of een heel weinig grond. Laat het namelijk zo zijn wat zij beweren, dat Mersenne tenminste in het jaar 1615 deze kromme heeft beschouwd, door hem genoemd la Roulette, en hierover de toenmalige Meetkundigen heeft ondervraagd; als het toch ook waar is wat Torricelli naar voren brengt (waarom dit niet zo is, zie ik niet, en zeggen zij, niet), dat deze zelfde lijn door Galileï al 45 jaar geleden (en dus tenminste al in het jaar 1599, hij publiceerde het boek immers in het jaar 1644) Cycloïde genoemd is. Hoezo, vraag ik dan, gaat het aan Mersenne ontzegd worden, zolang dit wordt gezegd? En hoewel ik niet ieder met gelijke munt wil terugbetalen, ce fut un sujet de rire en France; maar wij in elk geval, die misschien minder geneigd zijn tot uitlachen dan zijn Fransen, verbazen ons er tenminste over (wanneer we de woorden van Torricelli vergelijken met dit geschiedenisje) wat dat is van zo groot belang, dat aan deze zo grote klachten ten grondslag ligt. |
[ 79 ]
| (Alsof namelijk onze Neile uw Heuraet [<] van hetzelfde vergrijp zou beschuldigen, die meent dat hijzelf als eerste datzelfde naar voren brengt, wat al meer dan twee jaar bij de onzen wijd en zijd bekend is, echter zonder dat hij het weet, en door velen bewezen.) |
|
Maar misschien lijk ik teveel in te gaan op andermans zaken. Ondertussen zullen de geleerde heren (die ik hoogschat, en hun Mersenne) het me vergeven als ik die uitspraken liever soberder wil, waarmee de faam van een zeer geleerde, en vroeger heel verdienstelijke man zonder noodzaak wordt aangevallen. Ik zou veeleer hebben gewenst dat, als ze iets van zo groot belang bij zich hebben, dat ze niet willen dat het hun door anderen wordt ontnomen, zij het zelf openbaar maken, waardoor ze het veiliger aan zichzelf kunnen toekennen, en het ook meer van nut is voor algemeen gebruik; zodat het niet nodig is het tenslotte opnieuw voor zich op te eisen. Tenminste als, terwijl ze dit nalaten, het van anderen ergens anders vandaan vernemen, zij dan niet voorwenden dat hun onrecht gedaan wordt, of begrijpen dat het hun door henzelf wordt aangedaan. Maar na deze uitlatingen kom ik terug op onze Dettonville. Aangezien het zijne nu grotendeels, zij het met andere woorden, ook in het mijne voorkomt, ben ik wel eens van plan geweest de overeenkomstige plaatsen met de vinger aan te wijzen, en met dat doel had ik het al eerder nauwkeuriger willen doorlezen (nauwelijks anders namelijk dan zoals men zegt, canis ad Nilum*), hebben we binnen twee dagen dat genoemde doorgelezen, van alle hoofdzaken even proevend); en daar ik het tot nu toe wegens tijdgebrek niet heb kunnen doen, zal het voor u toch makkelijk te doen zijn, nu u elk van beide hebt bestudeerd. |
|
Ik wil echter niet dat u denkt dat ik dit zeg met de bedoeling, alsof ik iets wil afdoen aan de verdiensten van de geleerde heer; of iets van een slinkse verdenking koesteren; maar opdat tenminste werkelijk vaststaat, hoe het in dit soort zaken niet verbazend kan zijn, dat verschillende mensen, ver van elkaar, en niet door elkaar erop gewezen, terwijl ze bezig zijn met dezelfde Meetkundige zaken, op dezelfde meetkundige beschouwingen komen; en zo, dat de een de ander niet zomaar beschuldigt van diefstal (vooral in deze eeuw, die zo vruchtbaar is aan vernuften), of ook anderen ongegrond beledigt omdat hij zelf het als eerste zou hebben gevonden. Want gevonden is wel een kwestie van scherpzinnigheid, maar als eerste gevonden is een kwestie van geluk hebben; en met niet minder subtiliteit of scherpzinnigheid heeft meer dan eens iemand iets later gevonden, dat iemand anders (zonder dat hij het wist) als eerste had gevonden. Doch waarom ik denk dat de geleerde heer al deze problemen van hem nog niet helemaal doorzien had, toen hij ze voorlegde; en niet voordat hij geschriften had ingezien van anderen hierover, naar de heer Carcavi gestuurd, die een hulpmiddel kunnen zijn om zijn vondsten te polijsten en vervolmaken: er zijn veel redenen die het aannemelijk maken. In elk geval heeft de geleerde heer al vanaf het begin, toen hij zijn Problemen voor het eerst uiteenzette, erkend dat hij deze wel niet *) Lett. de hond aan de Nijl, "canis ad Nilum, bibens et fugiens", drinkend en vluchtend. Plinius, Naturalis historia, boek 8, 148/149: "Certum est iuxta Nilum amnem currentes lambere, ne crocodilorum aviditati occasionem praebeant", "Het is bekend dat honden langs de oever van de Nijl rennend drinken om vraatzuchtige krokodillen geen kans te geven.", Ned. vert. J. van Gelder, M. Nieuwenhuis, T. Peters, De Wereld (Amst. 2005). Alexander Ross, Arcana Microcosmi (1651/52), Book II, Chapter 13: "Other Crocodiles, chiefly the American, are gentle, the AEgyptian fierce and cruel, which is the cause that Dogges are so afraid to drink out of Nilus, when arose that proverb, Canis ad Nilum." John Wallis gebruikte "canis ad Nilum" ook in De sectionibus conicis (1655), Dedic. p. I 2. |
[ 80 ]
| allemaal kon oplossen; maar als intussen niet iemand anders ze opgelost zou hebben, dat hij wat hij zelf heeft opgelost, niet aan anderen zou misgunnen, om daaruit belangrijker dingen te verkrijgen dan wat al gevonden is [<]. U ziet hoe voorzichtig dit is gezegd. Ook vergis ik me, of zijn oplossingen (voorzover ik uit oppervlakkig inzien opmaak) berusten op kennis van de lengte van de Cycloïde-lijn, en de verdeling ervan in een gegeven verhouding (behalve dit is namelijk zijn 13e figuur [p. 7] niet in overeenstemming te bengen met alle aanwezige gevallen). En ofschoon hij de vondst ervan aan onze Wren toeschrijft, zal hij geacht moeten worden er niet van te hebben geweten voordat hij de brief van Wren heeft ingezien. |
| En hoezeer hij ook moeite doet deze vondst van Wren te verkleinen, en laat blijken dat zijn Fransen een bewijs ervan konden verschaffen toen deze bekend werd, toch kan hij het niet over zich verkrijgen te bevestigen dat deze eerder aan hem bekend was, of dat wie ook van zijn Fransen, zelfs niet privé, aan iemand heeft laten blijken van deze lijn de lengte te hebben doorzien, of de verdeling in een gegeven verhouding. (Maar intussen kunnen we behoefte voelen aan eerlijkheid, als ik zie wat met zijn Fransen vóór de aangekondigde datum voortdurend is gedeeld; waardoor ze, zo niet op een andere manier, tenminste op grond van dit ingeziene in staat zijn het gevraagde op te lossen.) |
|
Ik voeg er bovendien aan toe, dat de laatste vragen, die tenslotte zijn voorgelegd in die Histoire [p. 7], die afhangen van de verdeling van deze kromme in een gegeven verhouding, een aanwijzing zijn dat de lengte ervan, en van zijn delen, eerder onbekend was. En er schijnt geen andere reden te zijn, waarom die niet samen met de vorige werden voorgelegd. Maar als mijn gissing in deze zaak me heeft misleid, en hij (noem ik hem Pascal, of Dettonville?) zal zeggen dit alles lang geleden te hebben doorzien, betwist ik het niet, maar feliciteer ik hem met zijn vondsten. Nu ben ik nog niet in staat, om de al genoemde reden, over elk punt afzonderlijk mijn mening te zeggen. Toch zie ik niet waarom die dingen die ik enigszins heb beoordeeld niet correct zouden zijn, en naar behoren bewezen. En in het bijzonder die dingen (waarover u mijn mening wil weten) over de gelijkheid van een Parabolische en een Spiraalvormige lijn [fig. 38, laatste brief]. Ofschoon ik namelijk het bewijs ervan nog niet heb bestudeerd, daar die propositie toch waar is — en ik zelf eerder heb doorzien dat dit zo is, zowel anders, als op deze manier op grond van een bewijs met ingeschreven en omgeschreven figuren — ben ik niet geneigd te vermoeden dat de geleerde heer bij het bewijzen een fout heeft begaan. Wat ik des te vrijmoediger uitspreek, omdat ik begrijp dat Roberval vroeger heeft geklaagd, dat ik zonder reden had beweerd dat die propositie fout was; ik had die zeker niet zonder reden en ook niet geheel en al afgewezen, maar alleen |
[ 81 ]
|
het bewijs dat door Hobbes was aangevoerd, afgekeurd als onvoldoende*). De propositie zelf heb ik, zodra ik die had onderzocht, waar bevonden. De berekening, die hij helemaal weglaat, zich ermee tevreden stellend de grondslagen te hebben geleverd, hebben wij geheel laten zien, tot en met het geval dat hij had gekozen uit alle, namelijk over het zwaartepunt van het halve omwentelingslichaam van de halve cycloïde beschreven om de basis (en bijvoorbeeld bij omwenteling van het hele lichaam ervan, gedaan om de as). Ik had gedacht ook bij de overige gevallen (voordat het werk af zou zijn) de berekening uit te voeren; tenminste die van § 65 en 66 samen moet aangevuld worden. Maar aangezien intussen de verhandeling van Dettonville is verschenen, heb ik gemeend er verder niets aan toe te moeten voegen; opdat ik niet met zijn kalf lijk te ploegen [^]. Zodat u nu de verhandeling hebt zoals die in de maand maart geschreven was, en ook naar de zeer geëerde viscount Brouncker gestuurd en die nu geheel in dezelfde staat is uitgegeven. |
|
Ik had dit werk wel veel uitgebreider, en met meer vertoon kunnen uitbrengen, wat ook misschien voor beginnelingen en minder in deze zaken geoefenden meer welkom zou zijn geweest, als ik met de formaliteiten van definities, lemma's, problemen, theorema's en scholia stap voor stap had willen gaan, en overal lineaire bewijzen met een lang apparaat had willen toerusten. Maar ik geloof dat de aangename kortheid u niet minder zal bevallen, en in het weinige ligt veel; u die, zeker met een strenge vinger naar de bronnen verwezen, de kracht van een beknopt geleverd bewijs niet minder begrijpt, dan wanneer het met zoveel formaliteit heel lang zou zijn. Indiens u ergens in de veelvuldige berekening (wat heel goed mogelijk is) ontdekt dat er een getal in plaats van een ander getal is gezet, zult u er geen bezwaar tegen hebben het aan te wijzen en mij te vergeven. En dit is dan wat ik besloten had zowel over Zijn verhandeling als over de Onze te zeggen. Maar voordat ik de Cycloïde geheel laat voor wat hij is: het zal u niet onwelkom zijn geloof ik, als ik de overeenkomst met de Cissoïde laat zien [<]. ...
*) John Wallis, Elenchus geometriae Hobbianae (1655), p. 132. [Elenchus: terechtwijzing.] Thomas Hobbes, Elementorum philosophiae sectio prima (1655), 20.5, p. 177 (Engl. 1656, p. 227). Idem Six Lessons to the professors of the mathematiques, p. 53, 59. John Wallis, Due correction for Mr Hobbes (1656, txt), p. 128. Thomas Hobbes, Stigmai ..., or, Markes of the absurd geometry ... of John Wallis (1657, txt), p. 1. John Wallis, Hobbiani puncti dispunctio (1657), p. 3. (Arithmetica infinitorum, 1656, p. 30.)
|
Naar aanleiding hiervan kwam me in gedachten een zekere stelling van me waarover u niet ontevreden zult zijn, naar ik meen. U kent de 
Laat C het verlengde zijn van één van beide zijden, neem van A, tot aan de loodlijn P. Dan zal gelden (wegens de hoek van 60 graden) C = ½ E. En dus: 
Aangezien de Cissoïde ABCb door constructie zodanig tot stand is gebracht, dat de rechte GB (begrensd door de Cissoïde en de cirkelomtrek, en gericht naar A, het eind van de middellijn AD) doormidden gedeeld wordt door NH (loodrecht staand midden op middellijn AD): Als bovendien getrokken worden zowel de middellijn GNK, als de rechten KA en KB (die de middellijn AD ontmoet in L, en de omtrek in P) toont 
Gegeven de conoïde waarvan de Parabool ABC het snijvlak met de as is, en de driehoek ADC zoals gezegd werd. Ik zeg dat het bolle oppervlak van de Conoïde zich verhoudt tot de cirkel met diameter AC, zoals tot 2/3 AC zich verhoudt een rechte, gelijk aan de twee AD en DC, en de lijn E, die tot AC staat, zoals AC tot de drie zijden van driehoek ADC. 
en