Stampioen de Jonge 1) aan Christiaan Huygens
1645 [of 1644]*)
Manuscript in UB Leiden [HUG 45].

Stampioen de Jonge 1) aan Christiaan Huygens
1645 [of 1644]*)
Manuscript in UB Leiden [HUG 45].

|
Om vorders in de mathematijc te studeeren is voor eerst noodich het solveeren ende ontbinden van eenige geometrische Quaestien, daer toe heel bequaem sijn De hondert geometrische quaestien 2) van meester Sibrant hanssen 3), die alle Arithmetische door Calculatie, ende oock geometrische door passer en liniael moeten opgelost worden.
1) Jan Janszn. [Johan] Stampioen de Jonge [1610 - 1653], sinds 1644 wiskundeleraar van Constantijn jr en Christiaan. [ *) O.C. 22, p. 399, n. 21: 1644 lijkt waarschijnlijker.] 2) Hondert Geometrische questien met hare solutien, Amsterdam ca. 1612. [Zie Matthijs H Sitters, 'Meester in de meetkunde', in Nieuw Archief voor Wiskunde, dec. 2003, 309-16. OC, XI, 23-27, Ned.] 3) Sybrandt Hansz Cardinael [Zie J. van Maanen in NAW 5/4 nr.1 (2003) 51-55.] |
[ 6 ]
|
Om dan noch verder te gaen, ende oock op den hoochsten trap der Wisconst te comen, soo sijn inde snijdinge vande Conus, namentlijck inden Ellipsis, parabole, ende hiperbole, de alder subtijlste wetenschappen verborgen, die imant hier op de werelt sou connen bedencken; daer toe is noodich het Bouck De Elementa Conica Appolloni pergaei 4), die de fondamenten om daer toe te geraecken grondich aen wijst. Aengaende de Optica, ende het gene dat daer aen dependeert sijn Ceplerus 5) ende Vitellius 6) heel goet. Het slijpen van alle glaesen soo tot verre kijckers ende oock tot andere opticae saken is het bouck 7) van de Cartes 8) bequaem. Ende tot de perspectijf die mede een deel is vande Optica can marlois 9), Stevijn 10), ende de Vries 11) toe gebruickt worden. 4) Apollonii Pergaei Conicorum libri quatuor (ed. Commandino), Bologna 1566. [>] 5) Johann Kepler, Dioptrice, Basel 1611. 6) Opticae thesaurus. Alhazeni Arabis libri septem, ... Item Vitellonis .. libri X (ed. Risner), Basel 1572. 7) Discours de la methode ... Plus la dioptrique ..., Leiden 1637 [Ned. 1659, 2011]. 8) René Descartes. 9) Samuel Marolois, Oeuvres mathematiques, den Haag 1614; Perspective, dat is: de doorsichtige, Amst. 1638 [Fr. 1614-1615]. 10) Simon Stevin, Vande Deursichtighe, Leiden 1605. 11) Johan Vredeman de Vries, Perspectiva theoretica ac practica, Amst. 1647. [Perspective, 1604-05 (Ned.); Lat.] |
[ 7 ]
|
De Weech-const can heel volcomme ende perfeckt uit Stevijn 12) ende uit Diophantis 13) geleert worden. sijnde mede een van de fraeijste stucken inde matematic. Tot de fortificatie daer sijn marlois 14) ende fridach 15) heel goet toe. De Architectuier is niet beter als uit Schamotius 16) te leeren, die de beste ende bequaemste proportie daer in observeert. 12) Simon Stevin, De Beghinselen der Weeghconst, Leiden 1586. 13) Stampioen vergist zich hier. 14) Samuel Marolois, Fortificatie, dat is, sterckte bouwing, Amst. 1628]. 15) Adam Freitag, Architectura Militaris Nova, Leiden 1631, Fr. 1635. 16) Vincenzo Scamozzi, L'idea della architettura universale [2], Ven. 1615; Grontregulen der Bow-const, Amst. 1640. |
[ 8 ]
|
Om nu vorders inde Astronomie te studeeren, soo can men niet bequaemmers hebben als alle de boucken 17) van Lansbergen 18) die de nieuste, corexte, ende oock de lichtste sijn om daer uit te begrijpen: Ende dan voorts (deese verstaende) soo canmen daer op leesen Tolemeus 19), Ticho Brae 20), ende nicolaes Copernicus 21). &c.:
17) Opera omnia, Middelburg 1663. Triangulorum geometriae libri quatuor, Midd. 1591, Amst. 1631; Cyclometriae novae libri duo, Midd. 1616, 1628; Progymnasmata ... de motu solis, Midd. 1619, 1628; Chronologiae sacrae libri III, Midd. 1625; Commentationes in motum terrae, Midd. 1630 [Martinus Hortensius' vertaling van Bedenckingen, op den dagelijckschen, ende jaerlijckschen loop vanden Aerdt-cloot, Midd. 1629]; Uranometria, Midd. 1631; Tabulae motuum coelestium perpetuae, Midd. 1632. In quadrantem tum astronomicum tum geometricum; nec non in astrolabium introductio, Midd. 1635 [Verclaringhe van't ghebruyck des astronomischen ende geometrischen quadrants, Midd. 1628, 1630, 1633; en Verclaringhe van de platte sphaere van Ptolemaeus anders astrolabium genaemt, Midd. 1628]. 18) Philips Lansbergen. 19) Claudii Ptolemaei Magnae Constructionis, id est Perfectae coelestium motuum pertractationis, ... lib. XIII, Basel 1538. 20) Tycho Brahe, Astronomiae instauratae progymnasmata, 1602, en Astr. instaur. mechanica, 1598 / 1602. 21) Nicolaus Copernicus, De revolutionibus orbium coelestium, 1543 / 1617. |
[ 9 ]
|
Ende daernae oock Clavius 22) die van alle formen van sonne wijsers een goede onderrechtinge 23) geeft. Hier aen volcht de Astrologia, dat is (de Astronomi verstaende) om daer uit te judiceeren, van gepasseerde ende oock van toecoomende saecken: die heel bequaem geleert can worden uit guido 24), ransovius 25), alhasen 26), alcabitius 27). &c: Inde Arithmetica valt niet veel meer te doen, ten sij dat de sinnelijckheidt streckte tot den Algebra ofte Coss daer toe datmen voor eerst (voor imant die daer 22) Christoph Clavius. 23) Gnomonices libri octo, Rome 1581, [Fabrica et usus instrumenti ad horologiorum descriptionem peropportuni, Romae 1586; Ratio facilis ... solaria, Lov. 1595.] 24) Guidobaldo del Monte, Problematum astronomicorum libri VII, Ven. 1609. [Of: Guido Bonatti, Liber astronomicus, decem continens tractatus (Aug. Vind. 1491, Ven. 1506, Bas. 1550), zie Robert H. van Gent, 'The views of Christiaan Huygens on astrology'.] 25) Heinrich Rantzau, Tractatus Astrologicus, Frankfurt 1593 [... 1633]. 26) Opticae thesaurus. Alhazeni Arabis libri septem, ... De crepusculis ... (ed. Risner), Basel 1572. Cf. 6). 27) Alchabitius, Libellus ysagogicus Abdilazi ... ad magisterium iudiciorum astrorum, Ven. 1482 [1485]. |
[ 10 ]
|
noch niet ingedaen heeft) Antoni Smiters 28) diende te gebruicken 29), ende die verstaende datmen als dan voort gaet tot Christoffel Rudolff 30) ende daer nae tot Franciscus Vieta 31) ende oock het bouck van de Cartes 32) midts daer voordts bij practiseerende soo canmen daer door (namentlijck door het gebruick vande Letters) tot de hoochste kennisse van alle wetenschappen volcomentlijck geraecken. Niet dat het deese voorverhaelde boucken, alleen sullen doen, maer daer wert oock noch toe vereist; Vooreerst een clouck verstant, ten andere geduerige naersticheidt, ende eindelijck oock een volcome lust, ende nijver tot soodanige weetenschappen. die als dan, niet alle te gelijck, maer verlancksamerhant, ijder int particulier door langdurige studi connen vercregen worden. Oock selfs daer noch wat bij te practiseeren tot het gene datmen geleesen heeft, vordert veel meer, als altijt ende geduerich (sonder eijgen practijck) inde boucken te suffen. &c: Dit lesten wert op het alder hoochsten gerecommandeert. 28) Anthoni Smyters. 29) Arithmetica, dat is de reken-konste [1609 / 1612 (Deel 3: Reghel Coss ofte Algebra) / 1620 (1e, 2e)], 1661-63. [ P. Bockstaele, 'Een onbekende arithmetica van Anthoni Smyters', in Gewina 2-2, 1979.] 30) Christoff Rudolff, Die Coss (ed. Stifel), Königsberg 1553 [en Amst. 1615]. 31) François Viète, In artem analyticam isagoge seu Algebra nova, Leiden 1635 [1591]; Opera mathematica, Leiden 1646. 32) Discours de la methode ..., la geometrie, Leiden 1637 [Ned. 1659]. Cf. 7). |


|
Opm. 1. Stampioen noemt niet zijn eigen werk: Algebra ofte Nieuwe Stel-regel, 1639 (met portret en handtekening J. J.). Hierin na opdracht en voorwoord (9 blz) veel gedichten (28 blz), waarin de lof soms lichtelijk overdreven wordt, maar dan 366 blz met zo te zien stevige wiskunde (zie echter opm. 2). Het boek stond in de bibliotheek van vader Constantijn: Catal. 33, nr 241. Het komt ook voor in de catalogus van Thevenot (1694), p. 185. Eerder had Stampioen een 'Kort by-voeghsel der sphaerischer triangulen' gepubliceerd, bij tabellen van F. van Schooten sr. (1632). In 1634 presenteerde hij zich met een pamflet (^) als wiskundeleraar ("Om te leeren soo wel Bejaerde als aenkomende Persoonen"); en met: Solutie op alle de quaestien, openbaer aengeslegen ende voor-gestelt door Ezechiel de Decker, Rott. 1634. Resolutie ende ontbindinghe der twee vraegh-stucken, in den iare 1632, Rott. 1634. In 1638 was er al polemiek: Openbaeringe der valscher pracktycken, ghepleegt door Jacobus a Waessenaer ... over ... het Antwerpsch Vraegh-stuck, 's-Gravenhage 1638. Op 16 juli 1640 schreef Stampioen een brief aan Joachim Jungius en een brief aan Woldeck Weland (die zijn leermeester Jungius vereerde met een Strena mathematica, Leiden 1640). Broer Wilhelmus Jansz Stampioen publiceerde een almanak: Ephemeris sive annalis ofte Dagelyckx iournael op het iaer ... 1640, met een 'Toe-eygeninge Aen alle lief-hebberen der Wis-konst' en een overzicht van "Konsten ende wetenschappen" [<].
Stampioen had zich weinig bemind gemaakt bij het afnemen van examens, zie P. C. Molhuysen, Bronnen tot de geschiedenis der Leidsche universiteit, deel 2, p. 307 (Res. Cur. 5 nov. 1646):
Curatoren besloten aan de bevoegde instantie (de Staten van Holland) te vragen het recht van examen te geven aan de pas benoemde professor (zie ook p. 304).
Aanleiding was geweest de kritiek van Jacob van Wassenaer op de regel van Stampioen (Algebra, 25) "om den Teerling-wortel te trecken uyt twee-naemighe ghetallen", in Aenmerckingen op den nieuwen stel-regel van Johan Stampioen, d'Jonge (1639) — met op p. 23-29 een mooi verhaal over "een waren en oprechten Quacksalver, dat is, een die niet anders en wiste als te lieghen sonder schaemte" en een student uit Padua. En op p. 16-17, over Stampioens bijvoegsel bij de tabellen van F. van Schooten sr (1632): "niet anders als onbequame lappen, hier en daer uyt eenige boecken gescheurt".  (BNF) De professoren Gool (Golius) en Schoten (sr) vonden de kritiek "gefondeert" (Wassenaer, 1640, 86). De inzet van de weddenschap, 600 gulden, ging naar het "Arme Pest huys der Stadt Leyden" (p. 87). Stampioen drukte nog een Verclaringe over het gevoelen by de E: H: professoren matheseos der universiteyt tot Leyden uyt-ghesproken (1640), en Wis-konstigh ende reden-maetigh bewijs (1640). Van Wassenaer noemde het eerste een "schandelijck boecxken", en voelt zich door het tweede "gedwongen de selve [fauten] noch sijne penne noch den druck, maer alleenelijck sijn onwetenheyt toe te schrijven" (Den on-wissen wis-konstenaer, 1640, p. 77). Zie verder over die twist Bierens de Haan, 'Bouwstoffen' xxx, in Versl.Meded.Kon.Ak. 1878, p. 69-112 en H. Bosmans, 1927. Dirck Rembrantsz van Nierop, Des aertrycks beweging, en de sonne stilstant (1e ed. 1661) 1683, p. 39: "hooghmoet gaet voor de val: wy hebben deser gelijcke noch een voorbeelt van Joan Stampioen, geschiet omtrent den Jare 1640." Zie ook Journal tenu par Isaac Beeckman, IV, 218 en D. Lipstorp, Specimina (1653), p. 13, 85. |
|
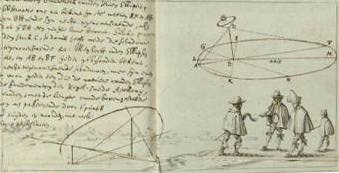
Wassenaer p. 59: de zon gaat niet onder (p. 75: poolshoogte 80° 45').
Gegeven: Een stuurman is op een onbekende plaats in een horizontaal veld, in de lente, de zon schijnt. Hij richt 3 stokken loodrecht op: in A van 6 voet, in B van 18 voet, in C van 8 voet, AB = 33 voet. Op het Groningse exemplaar staan aantekeningen van Frans van Schooten jr, die een oplossing publiceerde in Geometria (1649, p. 295 en 1659, p. 369); zie Jantien Dopper, A life of learning in Leiden : The mathematician Frans van Schooten (1615-1660), 2014, p. 266, 269.
|