Overzicht , Inleiding , Perspectief , glas , bepalingen , ander schaeu , werkstukken , strijding
Spiegels , keerpunt , verschil , holle spiegel , gedwaald , Noten
Stevins Deursichtighe
Boek 1 in Principal Works, IIB, p. 785-965. InleidingHet onderwerp van de Deursichtighe is de optica, zoals ook blijkt uit de titel L'Optique in de Franse vertaling van Stevins werken door Albert Girard (1634). In bepaling 1 noemt Stevin als onderdelen van het vakgebied:
Spiegelbeelden, lichtbreking, hoekmeting met een astrolabium ('platcloot'), de schaduw (G: skia) van de Zon, het hoort er allemaal bij. Betekende het woord 'schaeu' voor Stevin ook 'schaduw' (umbra)? Meestal wordt het gebruikt in de zin van 'dat wat je ziet' (schouw).
Dit noemen we nu het 'perspectief' 1 . Bepaling 4 zegt:
In het tweede boek staat "schaeu {Simulacrum Imago.}", daar gaat het om het 'beeld' in een spiegel van een "verschaeulickpunt {Spectatum.}". Niet alle onderwerpen uit de optica komen aan bod:
Het Cortbegryp der Deursichtighe noemt drie boeken:
Merkwaardig dat Perspectivis hier naast Verschaeuwing staat (is het een fout van de drukker, en moest het er boven staan bij de titel?). Op het volgende blad: Scenographia. Het eerste boek is een gedegen studie van het perspectief. Het tweede een korte verhandeling over spiegelbeelden in vlakke, bolle en holle spiegels. Het is vooral interessant om de foute conclusies die Stevin trekt uit enkele mooi beschreven proeven met 'clootspiegels'. Het derde boek ontbreekt. De 'wanschaeuwing' komt even aan de orde in het eerste boek in begeerte 1, en wordt genoemd in de Hemelloop (1608), als beschreven wordt dat Willem Barentsz en de zijnen op Nova Zembla de Zon zagen terwijl die onder de horizon was. Het onderwerp 'Breeckschaeuwen' vereiste duidelijk meer studie. Heeft Willebrord Snellius nog iets van Stevin geleerd waardoor hij de brekingswet kon vinden? Bij het vertalen van de Wisconstige Gedachtenissen in het Latijn zal hij er minstens even over nagedacht hebben. Aan het eind van het boek over spiegels (blz 108) noemt Stevin een onderwerp,
Na de theorie (beginselen) moet de praktijk (daet) komen, maar bij dit onderwerp is het er niet van gekomen. Wel op het gebied van de 'vrie wisconsten', de fundamentele wetenschappen die gaan over "Ghetal Grootheyt ende Ghewicht": 1: PerspectiefTekenenIn een tijd zonder fotografie was het een hele kunst om de werkelijkheid af te beelden met een goede gelijkenis. Een vak apart was de 'scenografie' (letterlijk: beschrijving van het toneel), waarvan Stevin een studie had gemaakt in verband met zijn 'Huysbau', een boek in wording. 2 In De Sterctenbouwing, uit 1594, staan twee ruimtelijke tekeningen (blz 26 en 32) met nog te veel evenwijdige lijnen.Maurits van Oranje wilde nu het vak ook beheersen. Anden Leser begint met:
Met goede tekeningen kun je de bedoeling duidelijk maken, en Zijn Vorstelijke Genade wilde meer "kennis der oirsaken" hebben dan "de bequaemste meesters in schilderie" hem konden geven.
(De tekeningen in het boek zijn groter.) |
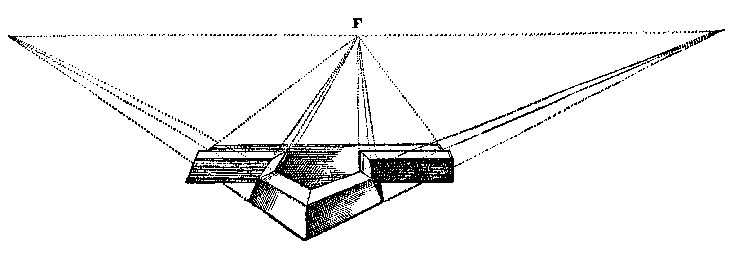
Een perspectivische tekening maak je met plattegrond en doorsnede. Eenvoudiger kan ook, zoals bij bepaling 1 staat:
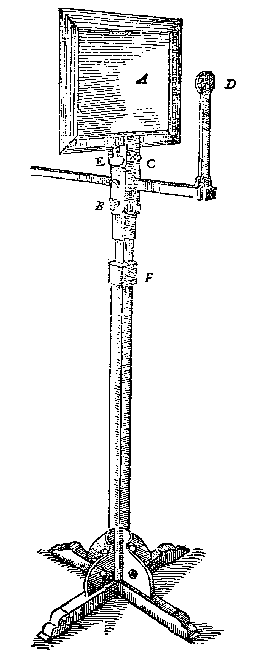
Stevin heeft zoiets gelezen bij Albrecht Durer. Diens houtsnede 'Tekenaar van een zittende man' laat zien hoe dat toegaat: met het oog op een vast punt (Leonardo da Vinci kende het principe ook). Zo'n toestel met een glas werd in opdracht van de prins gemaakt,
Maar het kan niet altijd op deze manier. Het blijft behelpen, zie ook Dürers 'Tekenaar van de kan' (touw nodig, oogpunt te ver van scherm). De andere praktische methode is: projectie met een lens in een donkere kamer, beschreven door Giambattista della Porta (boek 17.6). Stevin schijnt deze methode niet gekend te hebben, want bij zijn behandeling van de holle spiegel blijkt (zie hier onder) dat hij niet geloofde in de realiteit van een beeld dat in de lucht schijnt te hangen. Daadwerkelijk aftekenen is niet altijd mogelijk, omdat:
Met die regels van het perspectief, die Stevin gaat beschrijven, zijn de verkortingen en verlengingen op een gewenste schaal te tekenen.
BepalingenNa de bovengenoemde termen 'verschaeuwing', 'gront-, stantteyckening' definieert Stevin (blz 12):
Opvallend is dat Stevin de straal uit het oog laat komen (zie 7). Dit lijkt op de voorstelling van Euclides en Ptolemaeus: als we naar iets kijken, grijpen we het als het ware met het oog. Maar Stevin had wel Alhazen bestudeerd (zie 2), die uitlegde dat we een voorwerp zien doordat iets daarvandaan in ons oog komt. Een toelichting vond hij kennelijk niet nodig. Ook in het tweede boek, over spiegels, is een straal steeds een rechte lijn tussen twee punten. De optica was inderdaad een soort meetkunde (het woord 'licht' wordt in boek 2 alleen gebruikt bij een kaarsvlam in "een camer sonder ander licht"). Ander schaeuDan volgt in de eerste begeerte een kostelijk stukje dat enkele simpele proefjes beschrijft (opgenomen in het stuk over de taal, zie toelichting daar). Begeerd wordt dat de 'schaeu' van een punt ligt op de rechte lijn tussen dat punt en het oog. Dit is niet altijd waar:
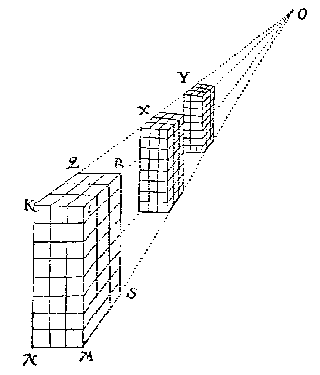
WerckstickenMet zes 'vertoogen' en acht 'wercksticken' behandelt Stevin op 65 bladzijden de meetkunde van het perspectief.Eerst het vinden der 'schaeu', dus het platte namaaksel. De lezer wordt aangespoord aktief mee te doen. Bijvoorbeeld op blz 19, als het gaat over het 'saempunt' van evenwijdige lijnen (verdwijnpunt):
De proef is ook te doen met een boek dat voor je ligt: houd twee linialen zo dat ze langs de zijkanten van het boek schijnen te lopen, en ze kruisen elkaar op ooghoogte.
Het verdwijnpunt van horizontale evenwijdige lijnen is even hoog als het oog.
CorthedenEen tweede gedeelte 'Vande Cortheden en Sekerheden opt Werck', geeft voorbeelden ter oplossing van problemen, in zes leden:
De oplossing is "een cleene lichamelicke bots" (nabootsing), een schaalmodel.
OogHet derde gedeelte van de 'Verschaeuwing' gaat over het vinden van het oog, wat ook van belang is in de kunst:
Deze mismaking, of 'anamorfose', was eerder genoemd: een mooi en geheim deel van het perspectief. 4
Geduldig legt Stevin de moeilijke materie duidelijk uit, voor een aantal bijzondere gevallen. Aan het eind staat een stuk dat misschien beter als inleiding had kunnen fungeren, omdat het gaat over simpele gevallen. Merck 2 (blz 77):
Meestal is de oorspronkelijke plaats van het oog niet te vinden, omdat er meer mogelijkheden zijn.
Er zijn vijf regels om snel te zien of een "verschaeuwing qualick ghedaen" is. StrijdingIn de Anhang, "om leering met gheen strijding te verduysteren", staan acht hoofdstukken over diverse zaken waarover de meningen verschillen. Bij voorbeeld over de vraag of je de regels altijd precies moet volgen (h. 6):
Opmerkelijk is nog dat prins Maurits bedacht dat een perspectieftekening ook is te berekenen:
Hij zal dit wel niet zonder hulp van Stevin gedaan hebben, maar de berekening (blz 90) geeft aan hoe ver de prins ging met zijn wiskundige belangstelling. Elders in de Wisconstige Gedachtenissen zijn veel van zulke voorbeelden te vinden.
2: SpiegelsCatoptricaStevin was al langer bekend met problemen uit de optica. Dit blijkt uit een opmerking in de opdracht van L'Arithmetique (1585):
De vader van Hugo de Groot las de klassieke werken over de optica. 5 Een werk over Catoptrica wordt aangekondigd in de Bewysconst (1595), Tsamespraeck blz 158:
In zijn boek over spiegels noemt Stevin nu, 20 jaar later, weer dezelfde klassieken (Alhazen ook in de Damphooghde). Hij heeft niet alleen de bekende proeven gedaan, maar ook zelf nieuwe bedacht. En op een belangrijk punt kwam hij tot een andere conclusie dan zijn beroemde voorgangers. Bepalingen 1, 2:
|
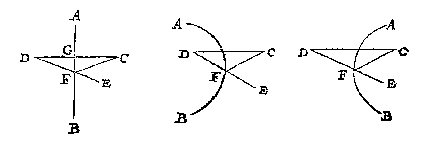
C is het 'verschaeulickpunt', D de 'schaeu' (het beeldpunt). Het 'oogh' E is weer gedefinieerd als "t'punt datmen neemt des oogs sienlick werck te doen". KeerpuntHoe kwam Stevin nu bij zo'n foute beeldvorming in de bolle en holle spiegel?De kern van het probleem wordt misschien het best onthuld in een mooie vergelijking in bepaling 7:
Punt F heet daarom het 'keerpunt'. En bij Stevin bepaalt dat keerpunt de beeldvorming, er is verder niets voor nodig:
Dit staat in voorstel 3, over de vlakke spiegel. En het klopt: het spiegelbeeld van de Zon kun je zien in een waterplas en in een klein spiegeltje.
Want in dat ene punt, het keerpunt, zijn kromme lijn en raaklijn hetzelfde. Voorwerpspunt en keerpunt zijn "alleenlick des schaeus oirsaeck". Opmerkelijk is dat in dit 5e voorstel het woord 'oog' niet voorkomt.
Het vinden van het keerpunt bij een bolvormige spiegel (voorstel 6) staat bekend als het probleem van Alhazen. Ook Stevin kon het niet algemeen wiskundig oplossen:
Gewoon proberen maar, "soo menichmael doen" totdat de hoeken gelijk zijn. Leonardo da Vinci had er een instrument voor ontworpen. VerschilZoals steeds wordt ook hier het geschilpunt behandeld in een Anhang, met verwijzing naar de bedoeling. Het gaat niet om de triomf 'ik weet het beter', maar om:
Verschuldigde hoogachting voor de bekritiseerden en eigen feilbaarheid staan voorop. En dat is maar goed ook, want hier is de kritiek van Stevin "ghemist"!
Een putje in de achterkant van een vlakke spiegel werkt als bol spiegeltje. Je ziet je neuspunt daarin dichterbij (en kleiner) dan in de vlakke spiegel. Uit zulke waarnemingen was opgemaakt dat het spiegelbeeld in een bolle spiegel dichterbij is dan in een vlakke spiegel. Maar Stevin denkt dat elk oog een ander spiegelbeeld ziet.
De tekening (later, op blz 107) maakt het duidelijk: F is de neuspunt, D en E zijn de ogen,
G en H zijn de 'keerpunten' voor de stralen.
Stevin zegt:
Wij zeggen nu: Merkwaardig is dat Stevin hier niet van toepassing vindt wat in begeerte 1 staat, de methode om de afstand te meten tot het beeld in een 'platspieghel':
Iets dat onbereikbaar ver weg is moet je bekijken vanuit twee standen, met driehoeksmeting. 6 Holle spiegelEen holle spiegel kan een reëel beeld maken, als het ware in de lucht hangend. Dat wist Stevin best, zie blz 108, waar hij voorstellen van Alhazen en Vitello (Witelo) noemt:
Bekende oorzaken: dat elk oog een ander beeld zou zien. Het is jammer dat die 'Spiegheldaet' niet is verschenen, misschien hadden we dan kunnen lezen dat Stevin tot andere gedachten was gekomen.
Inderdaad, het beeld kan niet achter je hoofd zijn. Stevin heeft kennelijk nooit het reële beeld opgevangen op een papiertje. Het probleem was waarschijnlijk dat er geen goede holle spiegel beschikbaar was.
Bij een stelling over het zwaartepunt van een parabool stond:
De holle spiegel kan werken als een brandspiegel doordat het beeld van de Zon voor de spiegel komt, en niet er achter. 7 GedwaaldStevin ging zelf uit van 'gedwaelde beginselen', namelijk:- het voorwerp werpt een beeld naar het keerpunt, en dit werpt het terug onder een zelfde hoek, - een beeldpunt in een holle of bolle spiegel is te vinden met een keerpunt en zijn raaklijn. Zo kreeg hij bij elk keerpunt een ander beeldpunt. Maar die beginselen waren niet ver afgedwaald van de 'ervaring':
Het tweede punt, schijnbaar één beeld, blijkt in deze proef:
Ja, maar wel onscherp, want je moet kijken naar de speld, dus je ogen accommoderen op het punt E. (Het is hier te zien door A resp. B met de handen op de juiste afstand af te schermen voor rechter- en linkeroog en te kijken naar een punt tussen je handen.)
Het laatste was in dit geval niet waar. 8
|
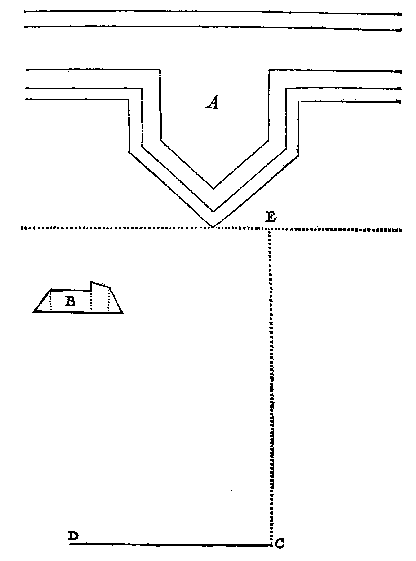 te verschaeuwen een seker bolwerck heel met eerde ghevult, op een rechte gordine, stelde sich voor de grontteyckening hier achter A, wiens verheven wercken, als wallen en bortsweeren daer op commende, anghewesen sijn mette stantteyckening B, voort bediet C de voet, waer op een lini verdocht als siendermaet even an CD, en rechthouckich op de vloer, dats hier opt plat des blats, t'eynde dier lini was de plaets des ooghs inde locht, van daer hy dat bolwerck wilde ghesien hebben, en volghende dat ghestelde, dede daer af de volghende verschaeuwing, welcke uyt sijn teyckening in hout ghesneen wiert, en ghedruckt alsmen hier achter siet.
te verschaeuwen een seker bolwerck heel met eerde ghevult, op een rechte gordine, stelde sich voor de grontteyckening hier achter A, wiens verheven wercken, als wallen en bortsweeren daer op commende, anghewesen sijn mette stantteyckening B, voort bediet C de voet, waer op een lini verdocht als siendermaet even an CD, en rechthouckich op de vloer, dats hier opt plat des blats, t'eynde dier lini was de plaets des ooghs inde locht, van daer hy dat bolwerck wilde ghesien hebben, en volghende dat ghestelde, dede daer af de volghende verschaeuwing, welcke uyt sijn teyckening in hout ghesneen wiert, en ghedruckt alsmen hier achter siet.
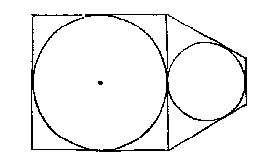 Als je schuin tegen een cirkel aankijkt zie je toch een ellips? Het ging om twee cirkels, gesneden in een elliptische kegel, waarvan de kleine de 'schaeu' is van de grote, met het oog in de top van de kegel. Daarna werd de grote op de grond gelegd; de 'schaeu' werd op een glas getekend en bekeken zoals bij de kegel. Tot zover klopt het.
Als je schuin tegen een cirkel aankijkt zie je toch een ellips? Het ging om twee cirkels, gesneden in een elliptische kegel, waarvan de kleine de 'schaeu' is van de grote, met het oog in de top van de kegel. Daarna werd de grote op de grond gelegd; de 'schaeu' werd op een glas getekend en bekeken zoals bij de kegel. Tot zover klopt het. 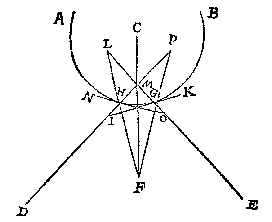
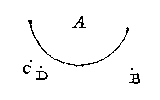 Int ghene hier gheseyt is sijn twee saken t'anmercken, d'een datter twee schaeuwen sijn in verscheyden plaetsen, d'ander datse inde gemeen sne der stralen een selfde schaeu schijnen te wesen. T'eerste blijckt daetlick aldus:
Int ghene hier gheseyt is sijn twee saken t'anmercken, d'een datter twee schaeuwen sijn in verscheyden plaetsen, d'ander datse inde gemeen sne der stralen een selfde schaeu schijnen te wesen. T'eerste blijckt daetlick aldus:
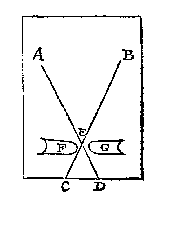 Men sal opt eynde eens tafels twee even hooghe brandende keersen stellen, ontrent een duym of twee lanck, in een camer sonder licht. [...] A, B:
Men sal opt eynde eens tafels twee even hooghe brandende keersen stellen, ontrent een duym of twee lanck, in een camer sonder licht. [...] A, B: