Home | Stevin | < Deursichtighe >
Schilderijen , Werkstuk 6 , 7 , 8 , pylaer , niet algemeen
[ 60 ]
N V V A N T' V I N D E N
D E S O O G H S.
Tot hier toe beschreven sijnde de manier der verschaeuwing, soo worter noch vereyscht kennis waermen om een gheteyckende schaeu in haer volcommenheydt te sien, het oogh moet stellen, dat is, hoemen vinden sal het punt inde locht, dat den verschaeuwer int verschaeuwen sich voor oogh ghestelt had. Om van t'welck by voorbeelt breeder te spreken, tis kennelick datmen schilderyen maeckt, welcke van vooren gesien seer mismaeckt schijnen, niet ghelijckende t'ghene sy beteyckenen moeten, maer de selve schilderie van ter sijden gesien deur een seker gaetken daer toe veroirdent, anwijsende de plaets des ooghs, sy ghelaten seer hupsch: En soo salmen verstaen ander schaeuwen die volcomelick na de const ghemaeckt sijn, sulcken plaets te hebben, alwaer het oogh ghestelt, de schilderye in haer volcommenheyt ghesien wort. Nu soo an alle schilderyen of schaeuwen sulcken gaetken ghestelt wierde, men soude dat niet behouven te soucken: Maer t'selve inde ghebruyck niet sijnde, wy sullen schrijven t'ghene ons van dies nu te vooren comt, als volght.
6 W E R C K S T V C K. 1 2 V O O R S T E L.
Wesende ghegeven een viersijdich of meersijdich plat, dat schaeu is van een ghegheven verschaeulick plat, op t'welck het glas int verschaeuwen een houck maeckte even an een ghegeven houck, en hebbende de selve schaeu ten minsten een sijde, of lini tusschen twee houcken * evewijdich mette glasgrondt: Het oogh te vinden. {*Parallela.}
I Voorbeelt vande schaeu eens verschaeulicke evewijdeghe
rechthouckighe vierhoucx.
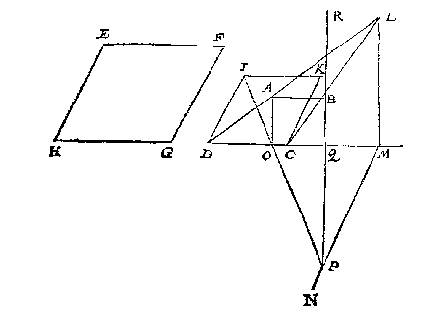
T G H E G H E V E N. Laet de vierhouck ABCD, hebbende twee evewijdege sijden AB en CD, schaeu sijn vande verschaeulicke evewijdeghe rechthouck EFGH, op wiens oneyndelick plat het glas int verschaeuwen rechthouckich stont.
[ 61 ]
De selve schaeu ABCD heeft twee linien, te weten AB, CD, ghetrocken tusschen twee houcken, die na den eysch des voorstels nootsakelick evewijdich mette glasgrondt moeten sijn deur het 2 voorstel.
T B E G H E E R D E. Wy moeten het oogh vinden.
T W E R C K.
Tis voor al te weten dat dit werck ghedaen wort deur verkeerde wech des 5 voorstels van t'vinden der schaeu, deur het ghegheven oogh mette rest: T'welc int gemeen geseyt wesende, wy sullen totte saeck commen. Angesien ABCD, schaeu sijnde van een evewijdeghe vierhouck, twee evewijdeghe sijden heeft, als AB met DC, en dat DC schaeu is der sijde als HG deur t'ghegeven, soo moest int verschaeuwen het glas strecken deur een der sijden EF, HG, of daer me evewijdich sijn deur het 3 voorstel: Maer het hebbe ghestreckt hoet wil, wy sullen de saeck hier, en in derghelijcke navolgende altijt nemen dattet deur een der sijden streckte, overmidts dattet al een selve oogh gheeft, soo wy int bewijs bethoonen sullen.
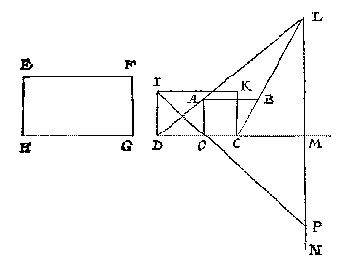
Om dan nu te weten deur welcke sijde, ick sie na de grootste der twee evewijdeghe AB, DC, de selve is DC, welcke schaeu sijnde vande lini HG deur t'ghegheven, soo streckte t'glas deur een sijde als HG. Dit soo sijnde, ick teycken op DC als lijckstandighe met HG, den vierhouck IKCD, gelijck metten vierhouck EFGH: Ick treck daer na DA en CB voorwaert, tot datse malcander ontmoeten int saempunt L, daer na LM als siendermaet rechthouckich op DC, of op haer verlangde als glasgrondt, en de oneyndelicke MN evewijdege met KC, voort AO rechthouckich op de glasgrondt DM, en van I deur O een lini tot datse de oneyndelicke MN ontmoet, als in P, daer na opt punt L een lini ghestelt of bedocht even an PM rechthouckich opt glas, t'eynde dier lini is t'begheerde oogh.
T B E W Y S.
Laet door t'ghedacht t'glas mette schaeu ABCD en de rest diemen verstaet int glas gheteyckent te wesen, scheydelick sijn vande vloer, draeyende t'selve glas op de glasgrondt DM als as, alsoo dattet rechthouckich stae op de vloer, dats oock rechthouckich op de verschaeulicke vierhouck IKCD: Daer na sy op P een sienderlijn ghestelt even ande siendermaet ML, en evewijdich mette selve: T'welck soo sijnde, het oogh ten eynde dier sienderlijn siet de schaeu ABCD dan overcommen met haer verschaeulicke rechthouck IKCD, sulcx dattet oogh daer tot sijn behoirlicke plaets is: Maer t'eynde dier lini en der boveschreven lini even an PM rechthouckich opt glas, is al een selve punt, daerom t'begheerde oogh is ghevonden na den eysch.
[ 62 ]
Maer mocht ymant nu segghen, de saeck is hier boven ghenomen al oft int verschaeuwen het glas ghestreckt hadde deur een vande sijden der verschaeulicke form, t'welck misschien verre van daer was evewijdich met DC. Hier op wort aldus gheantwoort: Staende het oogh voor de schaeu ABCD tot sijn behoirlicke plaets, en datmen vant selve oogh vier oneyndelicke linien treckt of bedenckt, deur de vier punten A, B, C, D, sy begrijpen een oneyndelicke vierhouckighe naelde {Pyramis.}, van sulcker ghedaente, dat alsmense snijt deur DC, met een plat rechthouckich opt glas, de sne is als IKCD, en alle ander sneen met die eerste sne evewijdich en verder vant oogh sijn grooter dan d'eerste, doch daer me ghelijck, en van elck dier verscheyden sneen is ABCD openbaerlick de schaeu ghesien uyt het selve oogh tot een selve plaets: Daerom alsmen het oogh begheert van een der ander sne men mach cortheyts en sekerheyts halven altijt soucken vande sne die t'glas gheraeckt, of dattet selve is, vant glas dat de voorste verschaeulicke sijde gheraeckt, als boven, en men heeft t'begheerde.
M E R C K T.
Wy hebben int boveschreven voorbeelt het glas rechthouckich ghegheven opt oneyndelick plat der verschaeulicke form, of anders gheseyt t'glas rechthouckich ghegheven op de vloer:
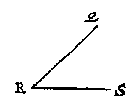 Maer soot daer op een scheefhouck maeckte, even, neem ick, an desen houck QRS, hebbende t'glas na de schaeu toe, ghelijck de lini QR na RS toe helt; In sulcken ghevalle salmen de wercking doen alsvooren, even al of t'glas op de vloer rechthouckich ghegheven waer, vindende PM, om alsoo een lini even an PM, te stellen opt punt L, uytgenomen datse opt glas niet rechthouckich en moet commen alsvooren, maer daer op een houck maken, even anden gegeven houck QRS, welverstaende dat de voorschreven lini even an PM, sijn sal int verdocht plat dat rechthouckich is op de glasgrondt DM, en dat oock rechthouckich is op t'glas,
Maer soot daer op een scheefhouck maeckte, even, neem ick, an desen houck QRS, hebbende t'glas na de schaeu toe, ghelijck de lini QR na RS toe helt; In sulcken ghevalle salmen de wercking doen alsvooren, even al of t'glas op de vloer rechthouckich ghegheven waer, vindende PM, om alsoo een lini even an PM, te stellen opt punt L, uytgenomen datse opt glas niet rechthouckich en moet commen alsvooren, maer daer op een houck maken, even anden gegeven houck QRS, welverstaende dat de voorschreven lini even an PM, sijn sal int verdocht plat dat rechthouckich is op de glasgrondt DM, en dat oock rechthouckich is op t'glas,
merckt noch dat sulcx als wy hier achter dit eerste voorbeelt gheseyt hebben vant glas scheefhouckich op de vloer, derghelijcke sal hem oock verstaen te meughen ghedaen worden inde volghende voorbeelden deser stof, alwaer cortheytshalven t'glas alleenelick rechthouckich op de vloer ghegheven sal worden.
Ander manier van wercking.
Ghelijck t'voorgaende werck ghedaen is deur verkeerde wech van t'vinden des schaeus achter het 11 voorstel, in der cortheden 3 lidts 1 voorbeelt, also canmen oock een wercking doen deur verkeerde wech des 5 voorbeelts van t'selve 3 lidt.
Om t'welck te verclaren, laet ABCD sijn de schaeu,EFGH de verschaeulicke form, en de rest alsvooren: Om hier af het oogh te vinden, ick teycken op DC, als lijckstandighe {Homologa.} met HG, den vierhouck IKCD, gelijck metten vierhouck EFGH, treck daer na DA en CB voorwaert, tot datse vergaren in L, voort de oneyndelicke LM evewijdeghe met DC, snyende CK of haer verlangde in N, en treck AB voorwaert soot noot is tot datse NC ontmoet in O, en teycken inde lini CD of haer verlangde t'punt P, alsoo dat CP even sy an CK;
[ 63 ]
Daer na treck ick van P deur O een rechte lini tot datse de oneyndelicke LM ontmoet, t'welck sy in M, voort stel ick opt punt L, een lini even an NM rechthouckich opt glas. T'welck soo sijnde, het uyterste dier lini moetet begeerde oogh sijn, waer af t'bewijs openbaer is, deur dien wy hier in gedaen hebben de verkeerde wercking van t'vinden der schaeu int 5 voorbeelt vant 3 lidt der cortheden.
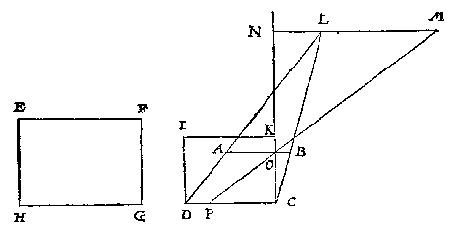
2 Voorbeelt vande schaeu eens verschaeulicke evewijdeghe
scheefhouckighe vierhoucx.
T G H E G H E V E N. Laet inde onderschreven form t'ghegheven en t'werck sijn als int eerste voorbeelt, uytghenomen dat de verschaeulicke vierhouck hier scheefhouckich is, voort dat ghetrocken sijnde IOP, soo en salmen gheen lini op L stellen even an PM als daer, maer de voornomde IOP ghetrocken sijnde, men sal noch trecken PQ, rechthouckich op de glasgrondt DM, en de selve PQ voorwaert tot R, alsoo dat QR even sy an ML, daer na opt punt R een lini ghestelt of bedocht even an PQ rechthouckich opt glas, t'eynde dier lini is
[ 64 ]
t'begheerde oogh, waer af t'bewijs deur t'voorgaende des 1 voorbeelts openbaer is.
De reden waerom int eerste voorbeelt de lini PQR niet ghetrocken en wiert als in dit tweede, is dat R openbaerlick altijt soude vallen in L, en daerom onnoodich ghetrocken.
3 Voorbeelt vande schaeu eens verschaeulicke vierhoucx met
alleenelick twee evewijdeghe sijden, die int verschaeu-
wen evewijdich waren mettet glas.
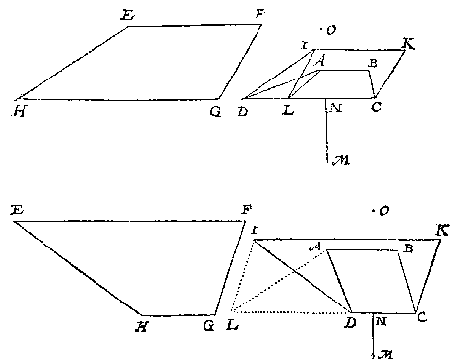
T G H E G H E V E N. Laet ABCD, hebbende twee evewijdeghe sijden als AB en CD, schaeu sijn vande verschaeulicken vierhouck hebbende alleenelick twee evewijdeghe sijden als EF, GH, die int verschaeuwen evewijdich waren mettet glas, op welcx vierhoucx EFGH oneyndelick plat, het glas mette sijde DC int verschaeuwen rechthouckich stont, en hebbende de lijckstandighe sijde met HG diens schaeu DC, inde verschaeuwing evewijdich ghehadt mettet glas.
T B E G H E E R D E. Wy moeten het oogh vinden.
T W E R C K.
Tsy dat int verschaeuwen het verschaeulick plat EFGH, mette sijde HG quam int glas, of niet, so stel ick nochtans my selven voor (om redenen verclaert int bewijs des 1 voorbeelts) dattet mette soodanige sijde daer in quam, sulcx dat DC is soo wel schaeu, als verschaeulicke der lijckstandighe sijde {Homologæ.} met HG: Dit soo sijnde, ick treck op DC als lijckstandighe met HG, den vierhouck IKCD, ghelijck metten vierhouck EFGH; Ick treck daer na van I tot DC of haer verlangde, de lini IL, evewijdeghe met KC, daer na AL.
[ 65 ]
T'welck soo sijnde ABCL is schaeu des evewijdeghen vierhoucx IKCL, ghelijck wy hier onder bewijsen sullen: Daer af ghesocht het oogh, wort bevonden deur het 2 voorbeelt deses voorstels, ten eynde, neem ick, der lini even an MN, gestelt opt punt O rechthouckich opt glas, t'welck ick segh t'begheerde oogh te sijn.
T B E W Y S.
Wy hebben int werck gheseyt dat ABCL schaeu is des vierhoucx IKCL, om van t'welck verclaring te doen ick segh aldus: T'punt A des vierhoucx ABCL, is schaeu van t'punt I, des vierhoucx IKCL, en t'punt L inde glasgrondt, is schaeu van sijn selven deur de 2 begheerte, en daerom is AL schaeu van IL deur het 1 voorstel; Maer AB is schaeu van IK, en BC van KC, daerom de vierhouck ABCL, is schaeu vande vierhouck IKCL, en vervolghens het oogh ghevonden van ABCL, moet oock sijn het oogh van ABCD, want de heele schaeu en haer deel gheen verscheyden ooghen en hebben.
M E R C K T.
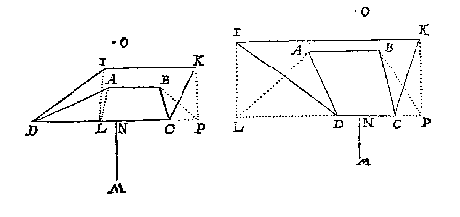
Men soude t'werck oock anders meughen doen met in plaets des scheefhouckighen evewijdeghen verschaeulicken vierhoucx IKCL te crijghen een rechthouck, t'welck aldus toegaet: Ick verteycken de voorgaende form IKCD als hier onder, en treck van I en K twee linien IL, KP rechthouckich op DC, of op haer verlangde, daer na AL met BP, en om de redenen int bewijs hier boven verclaert, soo is den vierhouck ABPL schaeu des verschaeulicken rechthouckighen vierhoucx IKPL: Daerom vande selve het oogh ghesocht deur het 1 voorbeelt, men salt vinden ter selver plaets alsvooren, te weten ten eynde der lini even an MN, ghestelt opt punt O rechthouckich opt glas.
4 Voorbeelt vande schaeu eens verschaeulicke vierhoucx met
alleenelick twee evewijdeghe sijden, die int verschaeuwen
onevewijdich waren mettet glas.
T G H E G H E V E N. Laet ABCD schaeu sijn van een verschaeulick plat, ghelijck metten verschaeulicken vierhouck EFGH, hebbende alleenelick twee evewijdeghe sijden als EH, FG, die int verschaeuwen onevewijdich waren mettet glas,
[ 66 ]
op welcx vierhoucx EFGH oneyndelick plat, het glas mette sijde DC int verschaeuwen rechthouckich stont, en hebbende de lijckstandighe sijde met HG diens schaeu DC, int verschaeuwen evewijdich ghehadt mettet glas.
T B E G H E E R D E. Wy moeten het oogh vinden.
T W E R C K.
Tsy dat int verschaeuwen het verschaeulick plat EFGH mette sijde HG quam int glas of niet, soo stel ick nochtans my selven voor (om redenen verclaert int bewijs des eersten voorbeelts) dattet met soodanighe sijde daer in quam, sulcx dat DC is soo wel schaeu als verschaeulicke der lijckstandighe sijde met HG: Dit soo sijnde, ick teycken op DC als lijckstandighe met HG, den vierhouck IKCD, ghelijck metten vierhouck EFGH, daer na KL even en evewijdeghe met CD; Voort van B tot in AD de lini BM, oock evewijdeghe met CD, t'welck soo wesende, MBCD is schaeu des evewijdeghen vierhoucx LKCD, ghelijck wy hier onder bewijsen sullen, daerom vande selve MBCD ghesocht het oogh, wort ghevonden deur het 2 voorbeelt deses voorstels ten eynde, neem ick, der lini even an NO, ghestelt op t'punt P rechthouckich opt glas, t'welck ick segh t'begheerde oogh te sijn.
T B E W Y S.
Wy hebben int werck gheseyt dat MBCD schaeu is des verschaeulicken evewijdeghen vierhoucx LKCD, om van t'welck verclaring te doen ick segh aldus:
Anghesien AD schaeu is van ID deur t'gestelde, soo moet de schaeu des punts L in AD wesen, sy moet oock sijn in BM, want alsoo KL evewijdeghe is mettet glas, en dat van B schaeu des punts K, ghetrocken is BM evewijdeghe met KL, soo moet de schaeu van KL sijn inde oneyndelicke BM deur het 2 voorstel, en daerom is MB schaeu van LK, en vervolghens de vierhouck MBCD schaeu van LKCD, en vervolghens het oogh ghevonden van MBCD, moet oock sijn het oogh van ABCD, want het deel der schaeu gheen ander oogh en heeft dan de gheheele schaeu.
M E R C K T.
Deur t'ghene gheseyt is int merck ant eynde des 3 voorbeelts, is kennelick datmen het werck oock soude meughen doen, met te trecken vande twee punten L en K twee hanghende op DC, vindende daer na de schaeu eens rechthouckighen vierhoucx deur het 1 voorbeelt.
[ 67 ]
5 Voorbeelt vande schaeu eens verschaeulicke vierhoucx met
vier onevewijdeghe sijden, ende voorste alleenelick eve-
wijdighe mette glasgront.
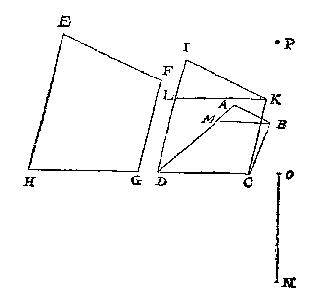
T G H E G H E V E N. Laet ABCD schaeu sijn van een verschaeulick plat gelijck metten verschaeulicken vierhouck EFGH, hebbende vier onevewijdeghe sijden, en op wiens oneyndelick plat het glas mette sijde DC int verschaeuwen rechthouckich stont, en hebbende de lijckstandighe sijde met HG diens schaeu DC, int verschaeuwen evewijdich ghehadt mettet glas.
T B E G H E E R D E. Wy moeten het oogh vinden.
T W E R C K.
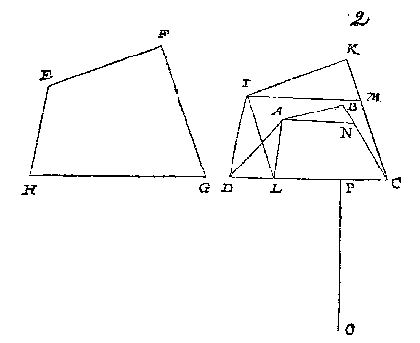
Tsy dat int verschaeuwen het verschaeulick plat EFGH, mette lijckstandige sijde van HG quam int glas of niet, so stel ick nochtans my selven voor (om redenen verclaert int bewijs des 1 voorbeelts) dattet met soodanige sijde daer in quam, sulcx dat DC is soo wel schaeu als verschaeulicke der lijckstandige {Homologæ.} met HG. Dit soo sijnde, ick teycken op DC als lijckstandighe met HG, den vierhouck IKCD, ghelijck metten vierhouck EFGH; Daer na van I twee linien, d'eene als IL evewijdich met KC, en commende L in DC of haer verlangde, d'ander IM even en evewijdeghe met LC: Daer na LA, en van A tot in BC de lini AN evewijdeghe met IM. T'welck soo wesende, ANCL is schaeu des evewijdeghen vierhoucx IMCL, ghelijck wy hier onder bewijsen sullen; Daerom vande selve ANCL ghesocht het oogh, wort bevonden deur het 2 voorbeelt deses voorstels, ten eynde, neem ick, der lini even an OP, ghestelt opt punt Q rechthouckich opt glas, t'welck ick segh t'begheert oogh te sijn.
[ 68 ]
T B E W Y S.
Wy hebben int werck gheseyt dat ANCL schaeu is des verschaeulicken evewijdeghen vierhoucx IMCL, om van t'welck verclaring te doen ick segh aldus: Anghesien t'punt A des vierhoucx ABCL, is schaeu van t'punt I des vierhoucx IMCD, en t'punt L inde glasgront is schaeu van sijn selven deur de 2 begheerte, daerom is AL schaeu van IL deur het 1 voorstel. Voort angesien BC schaeu is van KC deur t'ghestelde, soo moet de schaeu des punts M in BC wesen, sy moet oock sijn in AN, want alsoo IM evewijdich is mettet glas, en dat van A schaeu des punts I, ghetrocken is AN evewijdege met IM, soo moet de schaeu van IM sijn inde oneyndelicke AN deur het 2 voorstel, en daerom is AN schaeu van IM, en NC van MC, en vervolgens de vierhouck ANLC, schaeu van IMCL, en vervolghens het oogh ghevonden van ANCL, moet oock sijn het oogh van ABCD, want de heele schaeu gheen ander oogh en heeft dan haer deel.
M E R C K T.
Deur t'gene wy gheseyt hebben ant eynde des 3 voorbeelts, is kennelick datmen het werck oock soude meughen doen met te trecken vande twee punten I en M twee hanghende linien op DC, vindende daer na de schaeu eens rechthouckighen vierhoucx deur het 1 voorbeelt.
6 Voorbeelt van de schaeu eens verschaeulicke vierhoucx
wiens achterste sijde alleen evewijdighe is mette glasgrondt.
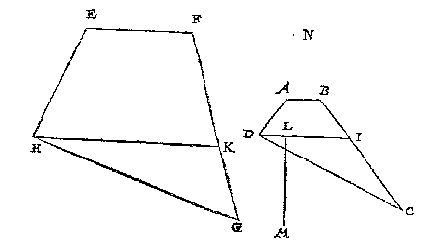
Int boveschreven 4 en 5 voorbeelt heeft des verschaeulicken vierhoucx voorste sijde evewijdich mettet glas gheweest, maer om de ghemeenheyt des voorstels te verclaren in vierhoucken diens achterste sijde alleenelick evewijdege is mette glasgrondt, soo laet ABCD schaeu sijn van een verschaeulicken vierhouck EFGH, hebbende vier onevewijdeghe sijden,
[ 69 ]
en op wiens oneyndelick plat het glas mettet punt C int verschaeuwen rechthouckich stont, en hebbende d'achterste sijde EF diens schaeu AB, int verschaeuwen evewijdich ghehadt mettet glas.
T B E G H E E R D E. Wy moeten het oogh vinden.
T W E R C K.
Ick treck DI evewijdeghe met AB, en commende I in BC; Daer na HK evewijdeghe met EF, en commende K in FG: T'welck soo sijnde, tis kennelick dat ABID is schaeu van EFKH, hebbende twee evewijdeghe sijden als EF met HK, daerom vande selve ABID ghesocht het oogh, wort bevonden deur het 3 voorbeelt deses voorstels ten eynde, neem ick, der lini even an LM ghestelt op t'punt N rechthouckich opt glas, t'welck openbaerlick t'begheerde oogh is.
7 Voorbeelt eens verschaeulicken vierhoucx hebbende alleene-
lick tusschen twee * teghenoverstaende houcken een ver-
dochte lini evewijdich mette glasgront. {*Oppositos angulos.}
By aldien de schaeu waer van een vierhouck als hier onder ABCD, schaeu van EFGH, alsoo dat de verdochte lini DB, waer evewijdich gheweest mette glasgrondt,
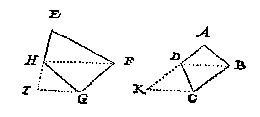 soo soude HF daer me oock moeten evewijdich gheweest hebben: Daerom ist kennelick datmen dan soude trecken HF, daer na EH oneyndelick voorwaert na I, en GI evewijdeghe met FH, S'ghelijcx DB, daer na AD oneyndelick voorwaert na K, en CK evewijdeghe met BD, en dat alsdan DBCK schaeu soude sijn van HFGI, waer af het oogh gevonden deur het 3 voorheelt, men sal t'begheerde hebben.
soo soude HF daer me oock moeten evewijdich gheweest hebben: Daerom ist kennelick datmen dan soude trecken HF, daer na EH oneyndelick voorwaert na I, en GI evewijdeghe met FH, S'ghelijcx DB, daer na AD oneyndelick voorwaert na K, en CK evewijdeghe met BD, en dat alsdan DBCK schaeu soude sijn van HFGI, waer af het oogh gevonden deur het 3 voorheelt, men sal t'begheerde hebben.
8 Voorbeelt van een verschaeulick rechtlinich plat meer dan
vier sijden hebbende.
Ghegheven sijnde de schaeu mette verschaeulicke form die meer dan vier sijden heeft, en de rest na t'inhoudt des voorstels, men sal om t'oogh te vinden uyt het selve verschaeulick plat verkiesen vier houck punten, soo dat daer tusschen bedocht of getrocken vier linien die een bequaem vierhouck maken, daer af een sijde int verschaeuwen evewijdich was mettet glas. S'ghelijcx salmen tusschen dier vier punten schaeuwen, trecken vier rechte linien en den vierhouck daer tusschen begrepen sal sijn schaeu van d'ander, daerom vande selve het oogh ghevonden deur een der boveschreven voorbeelden na de gheleghentheyt des verschaeulicken vierhoucx diemen alsoo gecreghen heeft, men sal oock hebben het oogh vande heele schaeu.
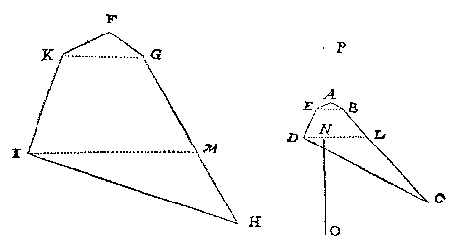
Laet by voorbeelt ABCDE schaeu sijn van een verschaeulick vijfhouck FGHIK, op wiens oneyndelick plat het glas mettet punt C int verschaeuwen rechthouckich stont, en hebbende de verdochte rechte lini van K tot G int verschaeuwen evewijdich ghehadt mettet glas.
T B E G H E E R D E. Wy moeten het oogh vinden.
[ 70 ]
T W E R C K.
Ick treck EB als schaeu van KG, en haer evewijdeghe DL, commende L in BC, daer na IM evewijdege met KG, en commende M in GH: T'welck soo sijnde, t'is kennelick dat EBLD schaeu is van KGMI, hebbende twee evewijdeghe sijden als KG met IM; Daerom vande selve EBLD ghesocht het oogh, wort bevonden deur het 3 voorbeelt deses voorstels ten eynde der lini, neem ick, even an NO, gestelt op t'punt P rechthouckich opt glas, t'welck openbaerlick t'begheerde oogh is.
T B E S L V Y T. Wesende dan ghegheven een viersijdich of meersijdich plat, dat schaeu is van een ghegheven verschaeulick plat, op t'welck het glas int verschaeuwen een houck maeckte even an een ghegeven houck, en hebbende de selve schaeu ten minsten een sijde of lini tusschen twee houcken evewijdich mette glasgrondt, wy hebben het oogh ghevonden, na den eysch.
M E R C K T.
Sooder bekent waer wat houck eenige vande sijden der verschaeulicke form int verschaeuwen op de glasgront maeckte, t'is openbaer dat deur de voorgaende manier ghevonden soude worden het oogh van alle ghegheven schaeu eens rechtlinich plats, om dat alle rechte lini ghetrocken uyt een houck der schaeu, evewijdich mette glasgrondt, schaeu is der lini ghetrocken inde verschaeulicke form uyt der ghelijcken houck oock evewijdich mette glasgrondt.
Maer anghesien het selden ghebeurt, dat in sulcke ghegheven schaeuwen soodanighen houck bekent is, soo soude dat inde daet weynich ghebruyck connen hebben. Doch als de ghegheven verschaeulicke form ten minsten heeft twee evewijdeghe sijden, of twee evewijdeghe linien die tusschen de houcken getrocken sijn of getrocken connen worden, soo isser deur ander wech eenichsins middel om daer toe te commen, waer af wy het volghende voorstel sullen beschrijven.
[ 71 ]
7 W E R C K S T V C K. 1 3 V O O R S T E L.
Wesende ghegeven een evewijdich viersijdich plat, dat schaeu is van een verschaeulick plat, op t'welck het glas int verschaeuwen een houck maeckte even an een ghegeven houck, en wesende de selve schaeu sonder eenighe sijde of lini die tusschen twee houcken evewijdich mette glasgrondt is, maer hebbende de verschaeulicke form ten minsten twee evewijdeghe sijden, of linien die tusschen de houcken ghetrocken sijn, of ghetrocken connen worden: Het oogh te vinden.
T G H E G H E V E N. Laet ABCD schaeu sijn, sonder eenighe sijde of lini die tusschen twee houcken evewijdich mette glasgrondt is, en dat vande verschaeulicke evewijdeghe vierhouck EFGH, op welcke het glas int verschaeuwen rechthouckich stont.
T B E G H E E R D E. Wy moeten het oogh vinden.
T W E R C K.
Ick treck DA en CB voorwaert, tot datse vergaren in I, sghelijcx BA en CD vergarende in K, daer na IK, en een oneyndelicke deur C, evewijdeghe met IK als LM glasgront beteyckenende, ick treck daer na AD voorwaert tot die oneyndelicke, ontmoetende de selve in L; S'ghelijcx AB voorwaert gherakende de selve oneyndelicke in M, en teycken int middel van LM t'punt N, en van N treck ick de oneyndelicke NO rechthouckich op LM; Daer na EP, alsoo dat den houck HEP even is anden houck PEF, treck daer na uyt de oneyndelicke NO, eenighe lini als OQ, alsoo dat den houck QON, even sy anden houck HEP, voort van L tot inde oneyndelicke NO, de lini LR evewijdeghe met QO, en beschrijf deur de drie punten L R M een booch; alwaer te ghedencken staet, dat wanneer den houck als HEF recht is als hier, soo valt des rondts middelpunt daer de booch op beschreven wort in N, en dien houck scherp sijnde, valt daer boven in NR, maer plomp sijnde valt daer onder inde verlangde RN: Voort treck ick EG; Daer na vande twee punten C en M, treck ick twee linien tot een selve punt des boochs, als tottet punt S, soo dat den houck CSM, even is anden houck GEF, (doch is te weten dattet wisconstich trecken {Mathematica operatio.} deses houcx, my int beschrijven van desen niet te vooren en quam, maer tuychwerckelick {Mechanicè.} macht ghedaen worden onder anderen met te snyen een papieren houck even an GEF, hebbende de sijden EG, EF lanck ghenouch, en desen papieren houck soo gheleyt, dat de sijden als EF, EG, gheraken de twee punten C M, en den uytersten punt als E inden omtreck, t'welck deur keering en wending ter eender en ander sijde daer toe ghebrocht can worden; Tis oock te weten, dat sulck gheraecksel des uytersten punts vant papier, alleenelick gheschien can wisconstelick, welverstaende int punt S, want van daer na M, soo comt dan dat punt buyten den omtreck, en van S na L vallet overal daer binnen. Dese tuychwerckelicke manier hebben wy liever hier ghestelt, dan de saeck ongheroert te laten, te meer op dat ander dieder lust toe hebben de wisconstighe wercking soucken meughen)
[ 72 ]
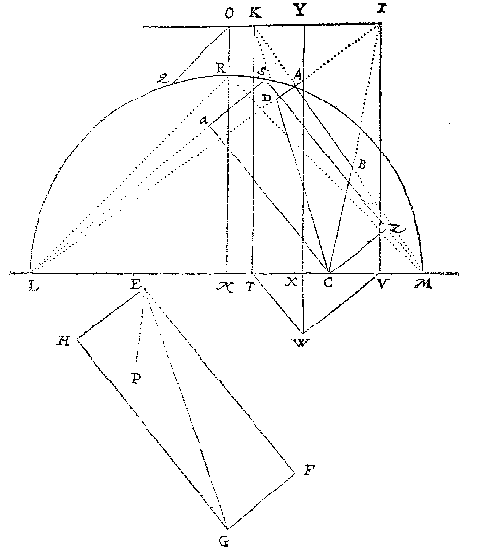
daer na LS, voort van K en I, twee linien KT, IV, rechthouckich op de oneyndelicke LM, voort VW evewijdeghe met SL, en van T tot inde oneyndelicke VW, de lini TW evewijdeghe met SM, daer na WX rechthouckich op LM, en WX voorwaert tot Y in KI, daer na stel ick opt punt Y een lini even an WX rechthouckich opt glas, t'welck soo sijnde, ick segh t'eynde der selve lini t'begheerde oogh te wesen.
T B E R E Y T S E L. Laet ghetrocken worden van C tot in SM de lini CZ, evewijdeghe met LS, sghelijcx van C tot in SL de lini Ca evewijdeghe met MS, daer na RM.
T B E W Y S.
Den houck LRN, is even anden houck MRN, en den houck HEP, even sijnde met LRN deur t'werck, is oock even anden houck PEF, daerom den houck LRM is even anden houck HEF; Maer den houck LSM (commende inde selve booch LRM ) is even anden selven houck LRM {21 voorst. 3 boucx Eucl.},
[ 73 ]
daerom den houck LSM is even anden houck HEF, voort is den houck CSZ even anden houck GEF, en ghelijck GF evewijdeghe is met HE, en GH met FE, alsoo CZ met aS, en Ca met ZS, daerom den vierhouck SZCa, als verschaeulicke vierhouck, is ghelijck metten vierhouck EFGH, en van desen vierhouck SZCa, wesende W de voet, of anders gheseyt wesende het oogh ten eynde der lini even an WX, ghestelt opt punt Y rechthouckich opt glas, soo is ABCD de schaeu, als de linien der form uytwijsen, lijckformich sijnde ande wercking van t'vinden der schaeu in der cortheden 3 lidts 6 voorbeelt. Maer wesende ABCD schaeu gesien uyt sulcken oogh, soo moet dat oogh oock t'begheerde sijn.
T B E S L V Y T. Wesende dan ghegheven een evewijdich viersijdich plat, dat schaeu is van een verschaeulick plat, op t'welck het glas int verschaeuwen een houck maeckte even an een ghegeven houck, en wesende de selve schaeu sonder eenige sijde of lini die tusschen twee houcken evesijdich mette glasgront is, maer hebbende de verschaeulicke form ten minsten twee evewijdeghe sijden, of linien die tusschen de houcken ghetrocken sijn, of ghetrocken connen worden, wy hebben het oogh ghevonden na den eysch.
8 W E R C K S T I C K. 1 4 V O O R S T E L.
Wesende ghegeven een viersijdich of meersijdich plat, dat schaeu is van een verschaeulick plat, op t'welck het glas int verschaeuwen een houck maeckte even an een ghegheven houck, en wesende de selve schaeu sonder eenighe sijde of lini die tusschen twee houcken evewijdich mette glasgrondt is, maer hebbende de verschaeulicke form ten minsten twee evewijdeghe sijden, of linien die tusschen de houcken ghetrocken sijn, of ghetrocken connen worden, en boven dien bekent sijnde den houck die eenighe sijde der ghegheven schaeu int verschaeuwen op de glasgrondt maeckte: Het oogh te vinden.
Dit 14 voorstel verschilt vant 13 daer in, dattet ghemeen is over alle veelsijdeghe platten {Multilatera plana.}, maer weerom daer teghen moeter bekent sijn wat houck eenighe lini der schaeu int verschaeuwen op de glasgrondt maeckte, t'welck int 13 voorstel niet noodich en was, om dat de glasgront uyt de ghegheven schaeu ghevonden wiert. Doch anghesien sulcken houck dickwils bekent wort in voorghestelde schaeuwen of schilderyen, deur eenighe ander bystaende linien diemen weet op de glasgront rechthouckich te commen, soo can t'vinden des ooghs van sulcke schaeuwen inde daet sijn ghebruyck hebben, waer deur wy t'selve hier beschrijven.
[ 74 ]
I Voorbeelt vande schaeu eens verschaeulicken vierhoucx met
alleenelick twee evewijdeghe sijden.
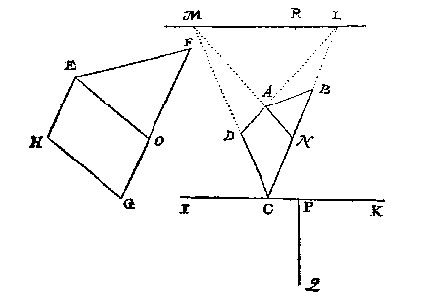
T G H E G H E V E N. Laet ABCD, de schaeu sijn vande verschaeulicke form EFGH inde vloer, waer af de twee sijden HE, GF, evewijdich sijn, maer d'ander twee GH, FE onevewijdich, en den houck D sy schaeu van H, en t'glas heb int verschaeuwen rechthouckich gheweest opt verschaeulick plat, en evewijdich met IK, die ick hier (tsy datser int verschaeuwen deur streckte of niet) doe strecken deur t'punt C sulcx dat den houck die eenighe sijde ick neem DC, int verschaeuwen op de glasgront maeckte, even was metten houck DCI.
T B E G H E E R D E. Wy moeten het oogh vinden.
T W E R C K.
Ick treck DA en CB voorwaert, tot datse vergaren in L, en deur L de oneyndelicke LM evewijdeghe met KI, daer na CD voorwaert tot datse die oneyndelicke ontmoet, t'welck sy in M, en van M deur A een lini tot datse CL ontmoet, t'welck sy in N, voort van E, tot in FG de lini EO, evewijdeghe met GH: Dit soo sijnde, ANCD is schaeu des evewijdeghen vierhoucx EOGH; Hier af het oogh ghevonden deur het 1 voorbeelt van desen [voorstel 7], t'welck sy ten eynde der lini even an PQ, ghestelt opt punt R, rechthouckich opt glas, men heeft t'begheerde, waer af t'bewijs openbaer is. deur de verkeerde wercking vant vinden der schaeu in der cortheden 3 lidts 6 voorbeelt.
2 Voorbeelt vande schaeu eens verschaeulicken rechtlinich plats
soot valt, doch hebbende ten minsten na t'inhoudt des
voorstels, twee evewijdeghe sijden of linien, die tusschen
de houcken ghetrocken sijn of ghetrocken connen worden.
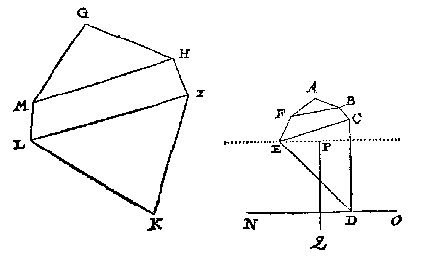
T G H E G H E V E N. Laet ABCDEF de schaeu sijn vande verschaeulicke form GHIKLM soot valt, doch hebbende de verdochte of ghetrocken linien tusschen de houcken M, H, en I, L, evewijdich, dat is MH evewijdich met LI, en den houck A sy schaeu van G, voort hebbe t'glas int verschaeuwen gheweest rechthouckich opt verschaeulick plat, en de glasgrondt evewijdich met NO, sulcx dat den houck die eenighe sijde ick neem ED int verschaeuwen op de glasgront maeckte, even was metten houck EDN.
T B E G H E E R D E. Wy moeten het oogh vinden.
[ 75 ]
T W E R C K.
Want den houck F schaeu is van M, en B van H, soo treck ick FB; S'ghelijcx want den houck E schaeu is van L, en C van I, soo treck ick EC, t'welck soo sijnde, de vierhouck FBCE, is schaeu des verschaeulicken vierhoucx MHIL, hebbende twee evewijdeghe sijden, daer af het oogh ghevonden deur het 1 voorbeelt, treckende de glasgront deur E evewijdich met NO, en de rest als int selve 1 voorbeelt, men vindt dat oogh ten eynde der lini, neem ick, even an PQ, ghestelt opt punt R rechthouckich opt glas, en men heeft t'begheerde: Waer af t'bewijs openbaer is.
T B E S L V Y T. Wesende dan ghegeven een viersijdich of meersijdich plat, dat schaeu is van een verschaeulick plat, opt welck het glas int verschaeuwen een houck maeckte, even an een ghegheven houck, en wesende de selve schaeu sonder eenighe sijde of lini die tusschen twee houcken evewijdich mette glasgront is, maer hebbende de verschaeulicke form ten minsten twee evewijdeghe sijden of linien, die tusschen de houcken ghetrocken sijn of getrocken connen worden, en boven dien bekent sijnde den houck die eenighe sijde der ghegheven schaeu int verschaeuwen op de glasgront maeckte, wy hebben het oogh ghevonden na den eysch.
V E R V O L G H.
Anghesien de schaeuwen van lichamen al in platten bestaen, soo volght daer uyt dattet oogh van een dier platten ghevonden sijnde deur de voorgaende reghelen, datmen heeft het oogh des heelen lichaems (uytgenomen van schaeuwen die int verschaeuwen met haer verschaeulicke form evewijdich waren, want die int besonder of alleen anghesien meughen het oogh overal hebben, om datse als int glas sijnde, gheen verandering en crijghen deur versetting des ooghs) Ia oock van alle ander omstaende schaeuwen der verschaeulicke formen by dat lichaem vervought, en t'selve angaende. Maer op dat alles noch claerder sy, sullen daer af voorbeelt stellen in deser voughen.
[ 76 ]
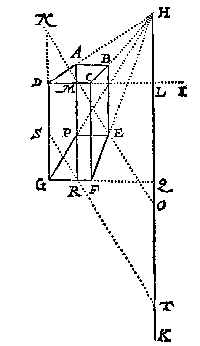
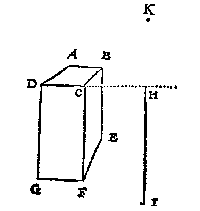 T G H E G H E V E N. Laet ABCDEFG sijn de schaeu eens verschaeulicken viercanten pylaers, die ghelijck is anden pylaer wiens hooghde DG, en sijde des gronts GF, en was het glas int verschaeuwen evewijdich mettet plat als DCFG tusschen den gront en het decksel: En heeft dese schaeu in haer de schaeuwen van drie platten als blijckt.
T G H E G H E V E N. Laet ABCDEFG sijn de schaeu eens verschaeulicken viercanten pylaers, die ghelijck is anden pylaer wiens hooghde DG, en sijde des gronts GF, en was het glas int verschaeuwen evewijdich mettet plat als DCFG tusschen den gront en het decksel: En heeft dese schaeu in haer de schaeuwen van drie platten als blijckt.
T B E G H E E R D E. Wy moeten het oogh vinden.
T W E R C K.
Ick stel my selven voor dattet glas int teyckenen streckte (t'sy dat den verschaeuwer dat int verschaeuwen soo mocht ghestelt hebben of niet) deur de evewijdege vierhouck DCFG, daerse int verschaeuwen evewijdich me was, en nemende het verschaeulick decksel diens schaeu ABCD, al oft op de vloer laghe, ick vinde deur het 1 voorbeelt des 12 voorstels het oogh als ten eynde der lini even, neem ick, an HI ghestelt opt punt K rechthouckich opt glas, welck oogh oock het oogh der heele verschaeulicke form moet sijn.
 I M E R C K.
I M E R C K.
Wy hebben int werck ghenomen dattet verschaeulick decksel diens schaeu ABCD op de vloer light: En volghende sulck ghestelde het oogh ghevonden: Maer want dat de eyghentlicke vloer niet en is, en dat ymant ant besluyt mocht twijfelen, soo sullen wy daer af verclaring doen.
Laet ABCDEFG een viercante pylaer sijn alsvooren, maer deurluchtich, waer in noch gheteyckent sijn de linien als volght: DA en CB sijn voortghetrocken tot datse versamen in H, en DC die als glasgront ghenomen wiert, is oneyndelick voortghetrocken na I, waer op rechthouckich ghetrocken de oneyndelicke HK, sy snijt DI in L; Daer nae getrocken AM rechthouckich op DI, en GD voortghetrocken tot N, alsoo dat DN even sy an DC, daer na van N deur M een rechte lini tot datse HK ontmoet in O, voort op het punt H een lini ghestelt even an OL, en rechthouckich opt plat daer de schaeu in is, het eynde der selve is het oogh, ghelijck int voorgaende werck ghevonden wiert.
Maer om nu te bethoonen dat dit soo wel het waer oogh is, als het oogh ghevonden deur wercking op den eyghen vloer, soo laet ghetrocken worden GH, en FE voorwaert, die vallen moet in H, daer na EP, evewijdege met FG, en commende P in GH, sulcx dat PEFG de schaeu beteyckent des verschaeulicken grondts inde eyghen vloer.
[ 77 ]
Om van dese schaeu PEFG het oogh te vinden, ick doe alsvooren, treckende de glasgrondt GF voorwaert, tot datse HK ontmoet in Q, en PR rechthouckich op de glasgrondt GQ, en teycken in GD t'punt S, alsoo dat GS even is an GF, daer na van S deur R een lini tot datse HK ontmoet in T, voort opt punt H een lini ghestelt even an TQ, en rechthouckich opt plat daer de schaeu in is, het eynde der selve moet openbaerlick het oogh wesen.
Maer dat dit eynde, en t'eynde der lini na t'eerste besluyt, al een selve punt is, volght daer uyt, dat TQ even is an OL, t'welck aldus bethoont wort: AM voortghetrocken sijnde, streckt deur P tot R, sulcx dat des rechthouckigen driehoucx SGR, sijde GR, even is an DM, en GS even an DN, deur t'werck, en daerom is de derde sijde NM, even en evewijdeghe met SR, en haer voortgetrocken linien als MO en RT, moeten inde twee rechthouckighe driehoucken MOL, RTQ, oock even en evewijdich sijn, alsoo oock moeten ML met RQ, en vervolghens, ghelijck wy bethoonen wilden, OL met TQ.
Hier uyt is oock openbaer ghenouch, datmen t'selve oogh alsoo vinden can deur d'ander twee afgaende vierhouckighe schaeuwen BEFC, APGD, te weten deur BEFC nemende de oneyndelicke daer FC in is voor glasgront: Maer deur de vierhouck APGD nemende de oneyndelicke daer GD in is voor glasgront, want deur de selve ghevonden de boveschreven lini die op H moet staen, sy sal oock even sijn met OL of TQ. Sulcx datmen uyt soodanighe vier vierhouckighe schaeuwen, verkiesen mach de bequaemste daer de tuychwerckelicke handeling de meeste sekerheyt in heeft.
2 M E R C K.
Want ymant dencken mocht, waerom hier int vinden des ooghs niet begost en wiert met voorbeelden wesende de schaeu een punt, lini, of driehouck, soo sullen wy daer af de reden verclaren, welcke int ghemeen gheseyt, is, datse gheen seker eenich besluyt, maer oneyndelicke besluyten hebben.
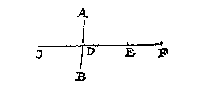 Om t'selve breeder te verclaren, en eerst van t'punt, soo laet AB een glas sijn over cant ghesien, C een verschaeulick punt, D sijn schaeu, daer na ghetrocken van C deur D de lini CDE, en E voor oogh ghenomen, tis kennelick dattet voor oogh van C sal meughen verstrecken. Maer CDE voortghetrocken tot F, soo sal F mette selve reden oock voor oogh van C meughen ghenomen worden, en alsoo met oneyndelicke ander.
Om t'selve breeder te verclaren, en eerst van t'punt, soo laet AB een glas sijn over cant ghesien, C een verschaeulick punt, D sijn schaeu, daer na ghetrocken van C deur D de lini CDE, en E voor oogh ghenomen, tis kennelick dattet voor oogh van C sal meughen verstrecken. Maer CDE voortghetrocken tot F, soo sal F mette selve reden oock voor oogh van C meughen ghenomen worden, en alsoo met oneyndelicke ander.
Angaende de lini ick segh aldus; soo t'een uyterste der verschaeulicke lini int glas is, t'ander daer buyten, de schaeu vant uyterste punt dat daer buyten is, wort ghesien totte selve plaets des glas deur oneyndelicke verscheyden ooghen, als boven gheseyt is, en t'ander eynde int glas wesende, sijn schaeu en verandert van plaets niet, deur verstelling des ooghs, daerom can de schaeu van sulcke lini uyt oneyndelicke verscheyden plaetsen ghesien worden.
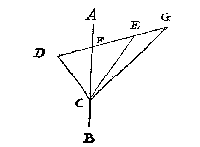 Om t'welck by voorbeelt te verclaren, Laet AB t'glas sijn over cant ghesien, CD een verschaeulicke lini, diens uyterste C int glas is, t'ander uyterste D daer buyten, E het oogh, van welck getrocken het strael ED, deurborende t'glas AB in F, als schaeu van D, en FC is de schaeu der verschaeulicke DC.
Om t'welck by voorbeelt te verclaren, Laet AB t'glas sijn over cant ghesien, CD een verschaeulicke lini, diens uyterste C int glas is, t'ander uyterste D daer buyten, E het oogh, van welck getrocken het strael ED, deurborende t'glas AB in F, als schaeu van D, en FC is de schaeu der verschaeulicke DC.
[ 78 ]
Maer om nu te bethoonen dat dese FC oock voor schaeu van DC can verstrecken, ghesien wesende van een ander oogh dan E, soo laet DE voortgetrocken worden tot G, welck punt G voor oogh genomen, het siet FC noch voor schaeu van DC, en alsoo met oneyndelicke ander.
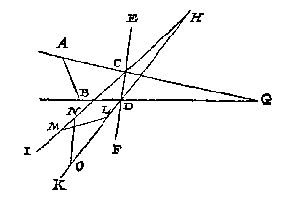
Maer de verschaeulicke lini t'eenemael buyten t'glas sijnde, als neem ick AB, diens schaeu CD, int glas EF overcant ghesien, en G het oogh, ick segh dat alle punt van ghedaente als H voor oogh ghenomen, soo can CD schaeu sijn van oneyndelicke ander verschaeulicke linien even an AB; want treckende van H deur C en D, twee linien als HCI, en HDK, en daer tusschen vervought de linien LM, NO even an AB, de selve LM, NO sijn openbaerlick verschaeulicke linien diens schaeu CD, en vervolghens de schaeu CD can oneyndelicke menichte van verscheyden ooghen hebben.
Tis wel waer dat soomen de verschaeulicke lini t'haerder ghestelde plaets gave, datmen alsdan het oogh nerghens versetten en can sonder verandering der schaeu te crijghen, doch wantet selden ghebeurt dat de verschaeulicke lini int glas onder of by, of inde schaeu met sulcke beteyckening ghestelt wort, soo en schijnet niet dat de vinding des ooghs deur sulcke manier seer begheert is.
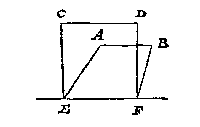
Nochtans om hier met een te verclaren, hoemen, of sulcx ghebeurde, daer me leven soude, soo laet AB schaeu sijn vande verschaeulicke CD, welcke schaeu AB evewijdich sijnde mette glasgront EF, alsoo gesien wiert doen t'glas rechthouckich stont op de glasgront, en ligghende de verschaeulicke CD inde vloer tot die ghegeven plaets oock evewijdich van EF, en dat nootsakelick deur dien CD daer af evewijdeghe is. Om hier van het oogh te vinden, ick treck vande twee punten C en D, op EF, eenighe twee evewijdeghe linien als CE, DF, tot op de glasgront EF. T'welck soo sijnde ick souck hier het oogh van dese ghegheven ABFE der verschaeulicke CDFE, na de manier des 13 voorstels, en heb t'begheerde.
Maer soo de schaeu niet evewijdich en waer mette glasgrondt, als neem ick dese lini AB, schaeu vande verschaeulicke CD, onevewijdich vande glasgrondt EF, men sal om t'oogh te vinden, aldus doen: Ick treck DC en BA voorwaert, tot datse inde glasgrondt vergaren in G (inde glasgrondt moetense vergaren, soo t'ghegheven warachtich is, te weten AB ware schaeu te sijn van CD, inder voughen als vooren:)
[ 79 ]
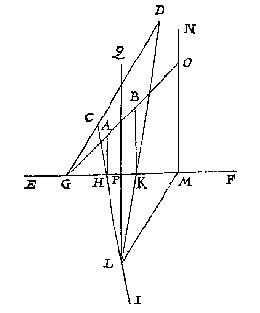 Ick treck daer na AH rechthouckich op EF, en van C verschaeulick punt des schaeus A, treck ick deur H de oneyndelicke CI; S'ghelijcx treck ick BK rechthouckich op EF, en van D verschaeulick punt des schaeus B, deur K de lini DL, ontmoetende de oneyndelicke CI in L, daer na LM evewijdeghe met GD, en gherakende de glasgront EF in M, voort de oneyndelicke MN rechthouckich op de selve glasgront, en GB voorwaert tot inde oneyndelicke MN, die gherakende in O, daer na LPQ rechthouckich op de glasgront EF, en snyende de selve in P, oock alsoo dat PQ even is an MO. Dit soo sijnde men sal opt punt Q een lini stellen even an LP, en opt glas sulcken houck makende als t'glas op de vloer, en t'uyterste dier lini is openbaerlick t'begheerde oogh.
Ick treck daer na AH rechthouckich op EF, en van C verschaeulick punt des schaeus A, treck ick deur H de oneyndelicke CI; S'ghelijcx treck ick BK rechthouckich op EF, en van D verschaeulick punt des schaeus B, deur K de lini DL, ontmoetende de oneyndelicke CI in L, daer na LM evewijdeghe met GD, en gherakende de glasgront EF in M, voort de oneyndelicke MN rechthouckich op de selve glasgront, en GB voorwaert tot inde oneyndelicke MN, die gherakende in O, daer na LPQ rechthouckich op de glasgront EF, en snyende de selve in P, oock alsoo dat PQ even is an MO. Dit soo sijnde men sal opt punt Q een lini stellen even an LP, en opt glas sulcken houck makende als t'glas op de vloer, en t'uyterste dier lini is openbaerlick t'begheerde oogh.
Angaende den driehouck die heeft oock oneyndelicke besluyten, want soo een sijde inde glasgront is, die en verandert niet deur beweging des ooghs, alsoo oock en doen d'ander twee linien, als t'oogh beweeght int oneyndelick strael vande verschaeulicken houckpunt deur haer schaeu, sulcx dat de heel schaeu des driehoucx dan sonder verandering blijft, altijt den verschaeulicken driehouck bedeckende, en daer me overcommende. Derghelijcke is oock te verstaen vande driehouck die de naeste sijde evewijdich heeft mette glasgrondt, om datmen int soucken des ooghs het glas daer deur mach doen strecken.
Maer soo de verste sijde des verschaeulicken driehoucx mettet glasgront evewijdich waer het oogh can oock tot oneyndelicke verscheyden plaetsen vallen. Om t'welck by voorbeelt te verclaren; Laet ABC de schaeu sijn eens verschaeulicken driehoucx ghelijck met DEF, voort is de verste sijde AB evewijdich neem ick mette glasgront GCH, diens glas int verschaeuwen rechthouckich stont opt plat der verschaeulicke form:
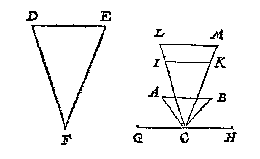 Laet nu vant punt C ghetrocken worden de twee linien CI, CK en IK, sulcx dat de driehouck IKC ghelijck is met DEF: Laet daer na CI voortghetrocken worden tot L, en CK tot M, daer na LM evewijdeghe met IK, en sal soo wel den driehouck LCM, als ICK, gelijck sijn met DEF. Dit soo wesende, tis openbaer meughelick het oogh alsoo te connen gestelt worden, datmen de twee punten A B (midts datmen verstae ABC te sijn int glas rechthouckich op de vloer) sal sien overcommen mette twee punten I K, als schaeuwen der selve, en sal dan ABC sijn schaeu der verschaeulicke IKC: Tis oock openbaer meughelick het oogh te connen ghestelt worden tot noch een ander plaets, alsoo datmen de voorschreven twee punten A, B, sal sien overcommen mette twee punten L, M, als schaeuwen der selve, en sal dan ABC, sijn schaeu der verschaeulicke form LMC, die soo wel als IKC, ghelijck sijnde met DFE, verstrecken elck voor ghegheven verschaeulicke form. Sulcx dat de schaeu ABC can ghesien worden van twee verscheyden ooghen, en vervolghens van oneyndelicke verscheyden ooghen.
Laet nu vant punt C ghetrocken worden de twee linien CI, CK en IK, sulcx dat de driehouck IKC ghelijck is met DEF: Laet daer na CI voortghetrocken worden tot L, en CK tot M, daer na LM evewijdeghe met IK, en sal soo wel den driehouck LCM, als ICK, gelijck sijn met DEF. Dit soo wesende, tis openbaer meughelick het oogh alsoo te connen gestelt worden, datmen de twee punten A B (midts datmen verstae ABC te sijn int glas rechthouckich op de vloer) sal sien overcommen mette twee punten I K, als schaeuwen der selve, en sal dan ABC sijn schaeu der verschaeulicke IKC: Tis oock openbaer meughelick het oogh te connen ghestelt worden tot noch een ander plaets, alsoo datmen de voorschreven twee punten A, B, sal sien overcommen mette twee punten L, M, als schaeuwen der selve, en sal dan ABC, sijn schaeu der verschaeulicke form LMC, die soo wel als IKC, ghelijck sijnde met DFE, verstrecken elck voor ghegheven verschaeulicke form. Sulcx dat de schaeu ABC can ghesien worden van twee verscheyden ooghen, en vervolghens van oneyndelicke verscheyden ooghen.
[ 80 ]
S'ghelijcx salmen oock verstaen vande driehouck sonder eenighe evewijdeghe mette glasgront. Laet by voorbeelt ABC schaeu sijn eens verschaeulicken driehoucx ghelijck met DEF: Voort is de sijde AB evewijdich, neem ick, mette glasgrondt GCH, diens glas int verschaeuwen rechthouckich stont opt plat der verschaeulicke form. Laet nu vant punt C ghetrocken worden de twee linien CI, CK, en IK, sulcx dat den driehouck IKC ghelijck is met DEF, en schaeu van ABC. Laet voort op een ander plaets geteyckent worden den driehouck LMC, oock ghelijck met DEF, maer grooter dan IKC, en dat tot sulcken plaets daermen de verschaeulicke lini LM can sien overcommen met haer schaeu AB. Dit soo wesende, de woorden der verclaring op de voorgaende form ghedaen, sullen oock dienen tot dese, en sal eyntlick besloten worden ABC schaeu te connen sijn van oneyndelicke verschaeulicke driehoucken gelijck met DEF uyt verscheyden ooghen ghesien.
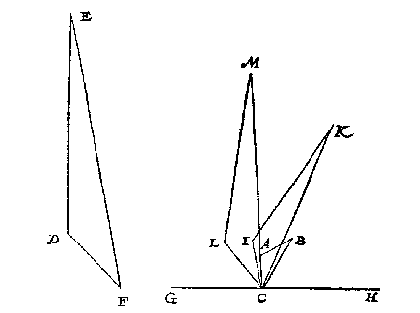
Maer soo den verschaeulicken driehouck ghegheven waer t'haerder plaets daerse int verschaeuwen was, soo en valter maer een besluyt. Om van t'welck by voorbeelt te spreken, laet den driehouck ABC de schaeu sijn des verschaeulicken driehoucx DEC, en FG de glasgrondt, diens glas opt verschaeulick plat rechthouckich quam. Om hier af het oogh te vinden, ick treck van E tot inde glasgrondt de lini EG evewijdeghe met DC, en van G deur B de oneyndelicke GBH, en CA voorwaert ontmoetende die oneyndelicke in H, en deur H de oneyndelicke HI evewijdege met FG, en AB voorwaert ontmoetende die oneyndelicke in I, en vande twee punten H en I twee linien rechthouckich op FG, als HF en IK; Daer na de oneyndelicke FL evewijdeghe met DC, en KM evewijdeghe met ED, en gerakende FL in M, daer na MN rechthouckich op FG, en de selve MN treck ick voort tot O in HI, daer na op O een lini ghestelt even an NM en rechthouckich opt glas; Het eynde dier lini is t'begheerde oogh.
[ 81 ]
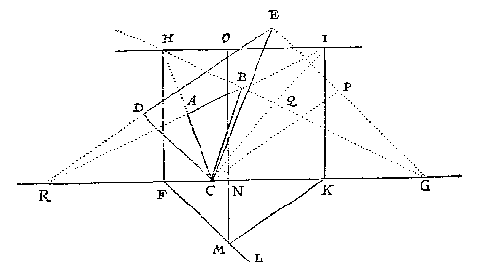
T B E R E Y T S E L V A N T B E W Y S. Ick treck CP even en evewijdege met DE, voort CI snyende GH in Q, en ED met BA voorwaert vergarende nootsakelick inde glasgront GF, t'welck sy in R.
T B E W Y S.
Dit bereytsel soo ghedaen sijnde, men siet een form van gedaente als die der cortheden 3 lidts 6 voorbeelt alwaer blijct dat ABQC schaeu is des verschaeulicken vierhoucx DEPC, en deur de verkeerde wercking van dien blijckt dattet oogh moet commen als boven gheseyt is.
Home | Simon Stevin | Deursichtighe | Verschaeuwing - d (top) | Vervolg
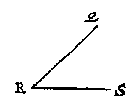 Maer soot daer op een scheefhouck maeckte, even, neem ick, an desen houck QRS, hebbende t'glas na de schaeu toe, ghelijck de lini QR na RS toe helt; In sulcken ghevalle salmen de wercking doen alsvooren, even al of t'glas op de vloer rechthouckich ghegheven waer, vindende PM, om alsoo een lini even an PM, te stellen opt punt L, uytgenomen datse opt glas niet rechthouckich en moet commen alsvooren, maer daer op een houck maken, even anden gegeven houck QRS, welverstaende dat de voorschreven lini even an PM, sijn sal int verdocht plat dat rechthouckich is op de glasgrondt DM, en dat oock rechthouckich is op t'glas,
Maer soot daer op een scheefhouck maeckte, even, neem ick, an desen houck QRS, hebbende t'glas na de schaeu toe, ghelijck de lini QR na RS toe helt; In sulcken ghevalle salmen de wercking doen alsvooren, even al of t'glas op de vloer rechthouckich ghegheven waer, vindende PM, om alsoo een lini even an PM, te stellen opt punt L, uytgenomen datse opt glas niet rechthouckich en moet commen alsvooren, maer daer op een houck maken, even anden gegeven houck QRS, welverstaende dat de voorschreven lini even an PM, sijn sal int verdocht plat dat rechthouckich is op de glasgrondt DM, en dat oock rechthouckich is op t'glas, 







 soo soude HF daer me oock moeten evewijdich gheweest hebben: Daerom ist kennelick datmen dan soude trecken HF, daer na EH oneyndelick voorwaert na I, en GI evewijdeghe met FH, S'ghelijcx DB, daer na AD oneyndelick voorwaert na K, en CK evewijdeghe met BD, en dat alsdan DBCK schaeu soude sijn van HFGI, waer af het oogh gevonden deur het 3 voorheelt, men sal t'begheerde hebben.
soo soude HF daer me oock moeten evewijdich gheweest hebben: Daerom ist kennelick datmen dan soude trecken HF, daer na EH oneyndelick voorwaert na I, en GI evewijdeghe met FH, S'ghelijcx DB, daer na AD oneyndelick voorwaert na K, en CK evewijdeghe met BD, en dat alsdan DBCK schaeu soude sijn van HFGI, waer af het oogh gevonden deur het 3 voorheelt, men sal t'begheerde hebben.



 T G H E G H E V E N. Laet ABCDEFG sijn de schaeu eens verschaeulicken viercanten pylaers, die ghelijck is anden pylaer wiens hooghde DG, en sijde des gronts GF, en was het glas int verschaeuwen evewijdich mettet plat als DCFG tusschen den gront en het decksel: En heeft dese schaeu in haer de schaeuwen van drie platten als blijckt.
T G H E G H E V E N. Laet ABCDEFG sijn de schaeu eens verschaeulicken viercanten pylaers, die ghelijck is anden pylaer wiens hooghde DG, en sijde des gronts GF, en was het glas int verschaeuwen evewijdich mettet plat als DCFG tusschen den gront en het decksel: En heeft dese schaeu in haer de schaeuwen van drie platten als blijckt.
 Om t'selve breeder te verclaren, en eerst van t'punt, soo laet AB een glas sijn over cant ghesien, C een verschaeulick punt, D sijn schaeu, daer na ghetrocken van C deur D de lini CDE, en E voor oogh ghenomen, tis kennelick dattet voor oogh van C sal meughen verstrecken. Maer CDE voortghetrocken tot F, soo sal F mette selve reden oock voor oogh van C meughen ghenomen worden, en alsoo met oneyndelicke ander.
Om t'selve breeder te verclaren, en eerst van t'punt, soo laet AB een glas sijn over cant ghesien, C een verschaeulick punt, D sijn schaeu, daer na ghetrocken van C deur D de lini CDE, en E voor oogh ghenomen, tis kennelick dattet voor oogh van C sal meughen verstrecken. Maer CDE voortghetrocken tot F, soo sal F mette selve reden oock voor oogh van C meughen ghenomen worden, en alsoo met oneyndelicke ander.  Om t'welck by voorbeelt te verclaren, Laet AB t'glas sijn over cant ghesien, CD een verschaeulicke lini, diens uyterste C int glas is, t'ander uyterste D daer buyten, E het oogh, van welck getrocken het strael ED, deurborende t'glas AB in F, als schaeu van D, en FC is de schaeu der verschaeulicke DC.
Om t'welck by voorbeelt te verclaren, Laet AB t'glas sijn over cant ghesien, CD een verschaeulicke lini, diens uyterste C int glas is, t'ander uyterste D daer buyten, E het oogh, van welck getrocken het strael ED, deurborende t'glas AB in F, als schaeu van D, en FC is de schaeu der verschaeulicke DC.


 Ick treck daer na AH rechthouckich op EF, en van C verschaeulick punt des schaeus A, treck ick deur H de oneyndelicke CI; S'ghelijcx treck ick BK rechthouckich op EF, en van D verschaeulick punt des schaeus B, deur K de lini DL, ontmoetende de oneyndelicke CI in L, daer na LM evewijdeghe met GD, en gherakende de glasgront EF in M, voort de oneyndelicke MN rechthouckich op de selve glasgront, en GB voorwaert tot inde oneyndelicke MN, die gherakende in O, daer na LPQ rechthouckich op de glasgront EF, en snyende de selve in P, oock alsoo dat PQ even is an MO. Dit soo sijnde men sal opt punt Q een lini stellen even an LP, en opt glas sulcken houck makende als t'glas op de vloer, en t'uyterste dier lini is openbaerlick t'begheerde oogh.
Ick treck daer na AH rechthouckich op EF, en van C verschaeulick punt des schaeus A, treck ick deur H de oneyndelicke CI; S'ghelijcx treck ick BK rechthouckich op EF, en van D verschaeulick punt des schaeus B, deur K de lini DL, ontmoetende de oneyndelicke CI in L, daer na LM evewijdeghe met GD, en gherakende de glasgront EF in M, voort de oneyndelicke MN rechthouckich op de selve glasgront, en GB voorwaert tot inde oneyndelicke MN, die gherakende in O, daer na LPQ rechthouckich op de glasgront EF, en snyende de selve in P, oock alsoo dat PQ even is an MO. Dit soo sijnde men sal opt punt Q een lini stellen even an LP, en opt glas sulcken houck makende als t'glas op de vloer, en t'uyterste dier lini is openbaerlick t'begheerde oogh.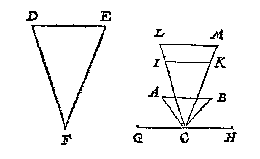 Laet nu vant punt C ghetrocken worden de twee linien CI, CK en IK, sulcx dat de driehouck IKC ghelijck is met DEF: Laet daer na CI voortghetrocken worden tot L, en CK tot M, daer na LM evewijdeghe met IK, en sal soo wel den driehouck LCM, als ICK, gelijck sijn met DEF. Dit soo wesende, tis openbaer meughelick het oogh alsoo te connen gestelt worden, datmen de twee punten A B (midts datmen verstae ABC te sijn int glas rechthouckich op de vloer) sal sien overcommen mette twee punten I K, als schaeuwen der selve, en sal dan ABC sijn schaeu der verschaeulicke IKC: Tis oock openbaer meughelick het oogh te connen ghestelt worden tot noch een ander plaets, alsoo datmen de voorschreven twee punten A, B, sal sien overcommen mette twee punten L, M, als schaeuwen der selve, en sal dan ABC, sijn schaeu der verschaeulicke form LMC, die soo wel als IKC, ghelijck sijnde met DFE, verstrecken elck voor ghegheven verschaeulicke form. Sulcx dat de schaeu ABC can ghesien worden van twee verscheyden ooghen, en vervolghens van oneyndelicke verscheyden ooghen.
Laet nu vant punt C ghetrocken worden de twee linien CI, CK en IK, sulcx dat de driehouck IKC ghelijck is met DEF: Laet daer na CI voortghetrocken worden tot L, en CK tot M, daer na LM evewijdeghe met IK, en sal soo wel den driehouck LCM, als ICK, gelijck sijn met DEF. Dit soo wesende, tis openbaer meughelick het oogh alsoo te connen gestelt worden, datmen de twee punten A B (midts datmen verstae ABC te sijn int glas rechthouckich op de vloer) sal sien overcommen mette twee punten I K, als schaeuwen der selve, en sal dan ABC sijn schaeu der verschaeulicke IKC: Tis oock openbaer meughelick het oogh te connen ghestelt worden tot noch een ander plaets, alsoo datmen de voorschreven twee punten A, B, sal sien overcommen mette twee punten L, M, als schaeuwen der selve, en sal dan ABC, sijn schaeu der verschaeulicke form LMC, die soo wel als IKC, ghelijck sijnde met DFE, verstrecken elck voor ghegheven verschaeulicke form. Sulcx dat de schaeu ABC can ghesien worden van twee verscheyden ooghen, en vervolghens van oneyndelicke verscheyden ooghen.