A   N   H   A   N   G,

Y ghedenckende van t'mishaghen dat ick somwylen ghehadt heb inde strijtredens  {Argumentis.} ettelicker schrijuers, welcke ghedreuen van haer ghemoet, ander persoonens dwalinghen in consten so verachtelick berispten, dat sy daermede een ghetuych gauen, van haer veel slimmer dwalinghen inde seden; ende dat my daer beneuen ouervloedighe stof  {Materia.} ontmoet was, om te connen weerlegghen veel dolinghen vande wichtighe ghedaenten duer sommighe beschreuen: Heb ghevreest int verclaren der seluer, den Leser van my een vermoeden te mueghen gheuen, van sulcx als my in anderen misuiel.
  Nochtans achtende hier beneuen, dattet gantschelick verswyghen (want wy met voorset daer af inde voorgaende boucken niet en hebben willen roeren, om de leering met gheen strijding  {Argumentatione.} te verduysteren) den sommighen eenich misverstant ende achterdeel mocht veroirsaken, heb my ghepoocht naer t'middel te trachten, ende inde plaets van veel besonder dwalinghen, alleen haer ghemeene oirspronck duer de twee eerstvolghende hooftsticken  {Capita.} te verclaren niet tot vermindering des naems van so weerdigen schrijuers, maer veel eer om die met danckbaerheyt te helpen vermeerderen, als van beweghende oirsaken haerder nacommers, sonder welcke veel besonderheden dickmael ongheroert souden ghebleuen hebben.

I^e   H O O F T S T I C, {Caput I.}  D A T   D E R   E V E S T A L T-

W I C H T I G H E N   O I R S A E C K   N I E T   E N   S C H V Y L T

onder de ronden beschreuen met d'uytersten der ermen.

E  redenen waerom euen swaerheden an euen ermen euestaltwichtich sijn, is duer ghemeene wetenschap bekent, maer niet also d'oirsaeck der euestaltwichticheyt van oneuen swaerheden an oneuen ermen met haer euerednich {Proportionales.}, welcke oirsaeck d'ouden ondersouckende, hebben die gheacht te schuylen onder de ronden beschreuen duer d'uytersten der ermen, als blijct by Aristoteles in Mechanicis met sijn nauolghers; T'welck wy ontkennen ende reden daer af aldus gheuen:
  E.   Dat stil hangt en beschrijft gheen rondt;
  A.   Twee euestaltwichtighe hanghen stil;
  E.   Twee euestaltwichtighe dan en beschrijuen gheen rondt.
  Ende veruolghens soo en isser gheen rondt; Maer alwaer gheen rondt en is daer en can t'rondt het ghene niet wesen daer eenige oirsaeck onder schuylt, waer duer de ronden hier t'ghene niet en sijn, daer d'oirsaeck der euestaltwichticheyt onder bestaet. Angaende (op dat wy des Bewysredens tweede voorstel {Syllogismi minorem.} verclaren) t'roersel ofte te [de] beschrijuing der ronden welcke haer ooghenschijnlick mach vertooghen, die en is niet eyghen der euestaltwichtighen, maer by gheualle, als duer windt, hurting, oft eenighe ander beweghing, met welcke niet alleen dese, maer oock d'oneuestaltwichtighe ronden connen beschrijuen. Tis dan openbaer dat dese oirsaeck in gheen ronden en bestaet, maer onder t'ghene int I^e voorstel des I^en boucx van de beghinselen der Weeghconst, daer af Wisconstlick {Mathematicè.} bethoocht is. Daerom die sulcke dwaling voor seker grondt namen, ten is gheen wonder dat sy, sonder te comen tot kennis der oirsaecken, oock sonder te crijghen form van Weeghconst, hemlien in veel valsche voorstellen oeffenden, die wy hier int besonder souden connen weerlegghen, maer sulcx laten om de redenen hier bouen verhaelt, te meer dat sy duer haer contrari, als t'voornoemde warachtighe, ghenouch bekent sijn.
  Men soude hier oock mueghen weerlegghen ettelicke voorstellen van scheefwichten, beschreuen duer Cardanus lib. 5. De proportionib. [1570] daer hyse raemt uyt seker houcken van linien oft platten, maer dat de selue ghemist sijn, is openbaer ghenouch duer het Wisconstich bewys van ander eueredenheyt {Proportione.}, int 19^e voorstel des I^en boucx van de beghinselen der Weeghconst.

I I^e   H O O F T S T I C K,   D A T   D E   G H E-

R O E R D E N   M E T   H A E R   B E L E T S E L E N   I N

gheen eueredenheyt {Proportione.} en bestaen.

Y  hebben inde voorreden der Weegdaet anden Leser, gheseyt, dat de gheroerden met haer beletselen niet euerednich en sijn, oock aldaer belooft elders van dies eyghentlicker bewys te doen, t'welck wy hier veroirdent hebben, alwaer weerleyt sullen worden de strijtredens {Argumenta.} vande ghene die de contrarie meynen, aldus:

Aristoteles int 4^e bouck der Natuer int hooftstuc des ydels met sijn nauolghers, willen, dat vallende twee lijckformighe lichamen duer de locht, ghelijck de swaerheyt van t'een tot die van t'ander, also diens tijt des duerlijdens tot desens, dat is, ghelijck swaerheyt tot swaerheyt, also belet tot belet. T'welck sijn meyning soo te wesen hy in verscheyden boucken opentlicker verclaert als lib. 6. Phys. oock lib. 1. 2. 3. 4. de Cælo, tot veel plaetsen.
Hier in heeft teghen Aristoteles gheschreuen Ioannes Taisnier Hannonius [1562], willende oock eueredenheyt, doch so, dat die twee voornomde lichamen in euen tijden duer euen langden des lochts vallen; In welcke meyning Cardanus oock is lib. 5. de Proportionib. prop. 110. Maer d'een noch d'ander en heeft de saeck ghetroffen, t'welck wy eerst met daetlicke eruaring verclaren sullen, ende daer naer d'oirsaeck bethoonen.
D'eruaring teghen Aristoteles is dese:
Laet nemen (soo den hoochgheleerden  H.  I A N   C O R N E T S   D E   G R O O T  vlietichste ondersoucker der Naturens verborghentheden, ende ick ghedaen hebben) twee loyen clooten d'een thienmael grooter en swaerder als d'ander, die laet t'samen vallen van 30 voeten hooch, op een bart oft yet daer sy merckelick gheluyt tegen gheuen, ende sal blijcken, dat de lichste gheen thienmael langher op wech en blijft dan de swaerste, maer datse t'samen so ghelijck opt bart vallen, dat haer beyde gheluyden een selue clop schijnt te wesen. S'ghelijcx beuint hem daetlick oock also, met twee euegroote lichamen in thienvoudighe reden der swaerheyt, daerom Aristoteles voornomde eueredenheyt is onrecht.
D'eruaring teghen Taisnier is dusdanich:
Neemt een cleen ynckel cort haerken boomwols, ende een paxken des selfden stijf in een ghebonden, weghende een pondt, ende van ghelijcke form mettet haerken, dese laet t'samen neeruallen van vijf ofte ses voeten hooch, ende d'eruaring sal betoogen dattet haerken (niet teghenstaende sijn stof veel dichter in een ghesloten is, dan des pacx, waer in veel ledighe plaets ofte locht is) wel vijuentwintich mael langher op wech blijft dan t'paxken. daerom sy en vallen na sijn meyning op gheen euen tijden duer euen langden des lochts.
Ander eruaring blijct oock teghen Taisnier int rijsend wicht, als in een lanck claer glas vol waters, t'welck gheroert, also datter veel lochtclooten ofte lochtbellen in commen, ende daerna stil ghehouden, de grootste bellen sullen snellick in een ooghenblick opcommen, de cleender niet soo ras, maer de minste als sandekens, soo traechlick als een slecke cruypt; t'welck verre is van euen tijden.
Dit is van d'eruaring gheseyt.
Daer rest nu noch d'oirsaeck te verclaren, waerom hier gheen eueredenheyt en is, aldus:
Yder roerende lichaem heeft eenich belet sijns roersels, dat van een vallende lichaem duer de locht, is t'ghenaecsel sijns vlacx {Superficiei.} teghen de locht,

daerom ontfangt t'meeste der ghelijcke lichamen wel t'meeste beletsel, maer ouermidts der lichamen grootheden met haer vlacken selfs niet euerednich en sijn (want twee teerlinghen in achtvoudighe reden, hebben haer vlacken alleen in viervoudighe) so en connen sy met die beletselen niet euerednich wesen, ende daerom ist dat de minste lichamen meer belet ontfangen, int ansien der eueredenheyt, dan de meeste, waerduer sy oock traechlicker neervallen.

  Ende of de vlacken schoon inde reden haerder grootheden waren, so is t'middel daer de lichamen duer vallen, alleen oock een oirsaeck die sulcke eueredenheyt weert, t'welck opentlick blijct in twee lichamen, t'een int water sinckende, t'ander daer op driuende, wiens beletselen der vlacken eenighe reden hebben, maer de tijden gheen, daerom en sijnse niet euerednich. Ymant sal hier toe mueghen segghen t'ghemeen woort D'ander parich {Caeteris paribus.}, dat is, hem sulcx alleen te verstaen van lichamen die beyde duer t'water sincken. Ick seg dat de voornomde eueredenheyt in sulcke oock niet en bestaet:
Om t'welck te bewysen so laet twee lichamen sijn, A t'swaerste, B t'lichste, die beyde int water sincken, ende tusschen hun besta de voornomde eueredenheyt. Dit soo wesende, tis kennelick datmen neuen A, ander oneindelicke menichte van lichamen voughen can, t'een lichter als t'ander, ende elck lichter als B, die alle daer in sincken. Nu yder van dese verleken met A, men sal allencx naerderen t'ghene bouen gheseyt is gheen eueredenheyt te wesen, dat is men sal naken de verlijcking eens lichaems dat sinct, met een dat niet en sinct: Maer dit soo naerderende, ende in A, B, de begheerde eueredenheyt bestaende, seker gheen dier oneindelicke menichte der lichamen met A verleken, en sullen die eueredenheyt hebben; want sooser in waer, sy en souden niet naerderen, t'welck teghen t'ghestelde is. Daerom soo wy voorghenomen hadden te verclaren, t'middel daer de lichamen duer vallen, is oock een oirsaeck die de voornomde eueredenheyt weert.

  Maer hier aldus bethoont hebbende, gheen eueredenheyt te bestaen tusschen de gheroerden met haer beletselen inde aldergheschicste voorbeelden, alwaer maer een eenvoudich strijcsel der vlacken en is teghen de locht, oft teghen t'water, soo en salder uyt noch stercker reden, gheen eueredenheyt wesen in ongheschicter voorbeelden van verscheyden stoffen, als in reetschappen van haut, ijser, en dier ghelijcke, want dit wort beolijt, dat besmeert, t'een can met een vochtich weer opswellen, t'ander verroesten, alle welcke (ick laet veel ander varen) de roerselen der reetschappen verlichten of beswaren.
Daerom soo gheseyt is inde boueschreuen voorreden der Weeghdaet, men sal hem op dese schijn van eueredenheyt niet verlaten, maer t'ghene Cardanus lib. 5. de Proportionibus in veel verscheyden voorstellen, met meer ander Schrijuers daer af besluyten, voor dwalinghen houden, sich vernoughende met de Wisconstighe kennis der euestaltwichticheyt van t'roerende ende het te roeren, als tottet voornemen ghenouch doende.

I I I^e.   H O O F T S T I C K,   D A T   D E   W E E G H-

C O N S T   E E N   B E S O N D E R   V R I E   W I S C O N S T   I S.

{Ars Mathematica.}

I S  wel waer, dat van der dinghen namen die de saeck niet en verduysteren, dickwijls onnoodighe verschillen {Quæstiones.} sijn, onder de welcke ick niet en ontken dit derde hooftstick te mueghen gherekent worden, doch anghesien wy de Weeghconst daert te pas ghecommen heeft, een vrye Wisconst ghenoemt hebben, soo moeten wy met corte woorden daer af wat redens gheven, aldus:
Ouermits de stof {Materia.} des ghetals al een ander is dan die der grootheyt, soo sijn de leeringhen haerder eyghenschappen te recht vanden anderen ghescheyden, ende elck voor een besonder Const ghehouden, als Telconst {Arithmetica.} ende Meetconst {Geometria.}, op dat elcke alsoo oirdentlicker, eyghentlicker, ende verstaenlicker soude mueghen beschreuen worden.
Ten anderen, want haer diepsinnighe ancleuinghen {Accidentia.} ons niet uyter natuer bekent en sijn, maer dat wy die leeren uyt de vergaerde schriften der ghene die duer besonder vliet hun daer in gheoeffent hebben, ia dickmael by gheualle ter kennis van yet besonders gherocht sijn, ende dat haer wetenschap den menschen daerenbouen seer nut is, soo wordense met recht vrye consten ghenoemt.
Ten derden, nadien de sekerheyt in haer bestaende, de ghewisheyt van d'ander Consten verre te bouen gaet, soo wordense billichlick daerbeneuen Wisconsten gheheeten. T'selue is om der ghelijcke redenen vande Weeghconst oock te oirdelen; want anghesien haer stof, te weten swaerheyt, al een ander is dan ghetal ofte grootheyt; oock dat de nutte eyghenschappen van dese, in diepsinnicheyt an d'eyghenschappen van die niet en wycken (t'welck daerin blijct, dat sy om sulcx laetst tot smenschen kennis ghecomen sijn, ende of sy v schoon licht dochten, dat muecht ghy d'onbegrijpelicke volmaectheyt der Duytsche spraeck dancken) Voorts dat sy duer haer uyterste beghinselen, in sulcken ghewisheyt bestaet als die, soo sal sy om haer ghemeene reden, een besonder vrye Wisconst ghenoemt worden.

  Yemant sal hier teghen mueghen segghen, dat de Meetconst tot haer bewysen dickmael ghebruyct wort, ende die daerom als afcomst {Species.} der Meetconst stellen. Ick antwoord de Telconst sulcx oock te ghebueren, nochtans een besonder vrye Wisconst blijuende. Want wat voornamelicke Vertoogen {Theoremata.} heeftse, diens grondelicke kennis duer de Meetconstighe formen niet vercreghen en wort? Ia die Meetconst seluer hoe soudese sonder ghetalen bestaen? Siet haer beghinselen als die van Euclides, hoe dickmael d'een form des anders dobbel, dese drie platten euen an die twee gheseyt worden.

T'blijct dan die voorstellen sonder t'behulp van ghetalen onbewyslijck te wesen, nochtans d'een des anders afcomst niet sijnde, ende alsoo oock met de Weeghconst.

  Angaende dat de Duersichtighe {Perspectiua} ende Spieghelconst {Catoptrica} voor gheen besonder vrye Wisconsten, maer als afcomsten der Meetconst gheacht sijn, by welcke yemandt de Weeghconst mocht willen verlijcken; hun redens sijn seer verscheyden, ouermidts de stof van dese, te weten swaerheyt, sulcx is, dat sy ghelijck de grootheyt, bestaet in alle voorghestelde wesentlicke saeck, met s'menschen groote nutbaerheyt; maer niet also de stof van die. Wy besluiten dan te recht, de Weeghconst een besonder vrye Wisconst te sijne, ghelijck ons voornemen was te bethoonen.

I I I I^e.   H O O F T S T I C K,   D A T   S O M M I G H E

V O O R G A E N D E   B E W Y S E N   D V E R   T'B E H V L P

der ghetalen Wisconstich {Mathematicæ.} siin.

E  gheleerden maken onderscheyt tusschen Wisconstich ende Werckelick {Mechanicam} bewys: T'welck niet sonder reden en is, want dat is ghemeen ouer allen, oock grondelick d'oirsaeck verclarende, dit besonder alleenlick op t'ghegeuen, sonder kennis der reden waerom dat also gheschiet. Als by voorbeelt, yemant om te bewysen dattet viercant der langste sijde eens rechthouckich driehoucx, euen is ande twee viercanten van d'ander sijden, neemt een driehouck, diens cortste sijde van 3 voeten, d'ander van 4, de derde van 5 voeten is, de selue wort rechthouckich beuonden; Bethoont daer mede dattet viercant der langste sijde 25, euen is ande viercanten van d'ander twee sijden, als 16 ende 9. Maer dit is alleenlick bewys van dat voorghestelde, waer uyt niet en volght sulcx ouer alle rechthouckighe driehoucken soo te moeten wesen, oock en sietmen daer duer d'oirsaeck niet, waerom dat also ghebuert. ende ouermits dit aldus werckelick gheschiet, so wordet daerom oock werckelick bewys gheheeten. Maer t'betooch van sulcx duer Euclides ghedaen int 47^e voorstel des I^en boucx, is ghemeen ouer allen, anwysende duer d'uyterste beghinselen, de reden waerom dat so is, ende niet anders sijn en can; t'selue wort om sulcke ghewisheyt Wisconstich ghenoemt, t'welck de Wisconstnaers {Mathematici} om de redenen hier vooren verhaelt, lieuer ghebruycken dant werckelick duer ghetalen.
Yemandt mocht nu segghen; Dit so sijnde, waerom hebdy dan de bewysen der 4^e, 11^e, 12^e, 18^e, voorstellen des 2^en boucx vande beghinselen der Weeghconst, duer ghetalen ghedaen? D'antwoort valt daer op, dat de ghetalen der bewysen ons op tweederley manieren ontmoeten, d'eene die als palen {Termini.} alleenlick de redenen {Rationes.} ende eueredenheden {Proportiones.} der deelen des voorghestelden forms verclaren, d'ander de menichvuldicheyt {Quantitatem.};

T'bewys duer die is Wisconstich, wanttet hem op alle afcomsten {Species.} des voorghestelden forms verstaet, ende d'oirsaken verclaert, maer dese [maer duer dese] niet om de contrarie redenen. T'welck Eutochius uytleggher {Commentator.} van Appollonius int 11^e voorstel des I^en boucx*) alsoo mede verstaet segghende: Niemant en beroer hem hier in dat dit duer de ghetalen bethoont is, want d'ouden pleghen sulcke bewysinghen te ghebruycken, so sy doch beter Wisconstich siin dan Telconstich, om de eueredenheyts wil; Merct oock dattet begheerde Telconstich is, want de eueredenheden, ende de menichvuldicheden der eueredenheden, oock de menichvuldighinghen {Multiplicationes.}, siin ten eersten in ghetalen, ten anderen duer ghetalen inde grootheden, na t'oirdeel van hem die aldus gheschreuen heeft:

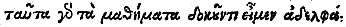
tauta gar ta mathèmata dokounti eimen adelpha.

dat is, dese Consten alle een moers kinderen te schijnen.
Nu soude ymant mueghen voortbrengen, dat Ptolæmeus, Archimedes, Appollonius, Commandinus, Regiomontanus, ende meer ander in der ghelijcke voorstellen, alle palen met gheen so uytghedruckte ghetalen en beteeckenen, als hier ghedaen is. Daerop antwoord ick, dat met alsulcke reden als sy segghen van der palen tweevoudicheyt, drievoudicheyt, mette selue salmen oock mueghen spreken daert te pas comt, van haer t'welfvoudicheyt, als AD tot RD int voornomde 23^e voorstel, ende van haer reden als 37 tot 23, ghelijck AR tot RD des boueschreuen 11^e voorstels, ende also met allen anderen, want sulcke linien in yder voorghestelde form dier afcomst, gheen ander reden en hebben. Nu anghesien datmen int ondersoucken der eyghenschap sulcker formen, dese ghetalen ghebruyct, die ons als seker anwys, met lichticheyt tot claer verstant der saeck brenghen, soo ist nut int beschrijuen der seluer, die ghetalen daer oock by te setten, om voor anderen niet duyster na te laten, t'ghene den Vinders {Inventoribus} selfs licht ende openbaer was. Want sulcx is t'recht Wisconstich bewys, t'voorghestelde duer d'oirsaken verclarende; T'welck ons voornemen was te bethoonen.

  Angaende sommighe bewysen des eersten boucx vande beghinselen der Weeghconst, oock des Waterwichts, inde welcke de swaerheden duer ghetal ende bekent ghewicht, als ponden, beteeckent sijn, t'welck yemant voor gheen Wisconstighe, maer voor werckelicke handeling mocht achten; die sal weten, dat beneuen soodanighe, oock mede ghestelt sijn haer Wisconstighe bewysen, als int I^e voorbeelt des eersten voorstels van t'eerste bouck, alwaer duer ghetalen ende bekent ghewicht, des voorstels inhoudt bethoont is, maer int tweede voorbeelt, is t'selue oock Wisconstelick bewesen, ende also met d'ander. Inder voughen dattet werckelick bewys tot meerder claerheyt somwylen bij t'Wisconstich ghevoucht is.

---

  [ *)  Geciteerd eb vertaald in Waterwicht, p. 6, met: "int eerste dier keghelsche boucken dat wy dencken int Duytsch te laten uytgaen".
Zie voor de uitspraak van Eutochius: Apollonii Pergaei Conicorum libri quattuor (Bon. 1566), 14v .]

V^e.   H O O F T S T I C K,   W E L C K   V E R C L A-

R I N G   I S   O P   H E T   V I I I^e   V O O R S T E L   D E  R

beghinselen des Waterwichts.

A E R  is int boueschreuen 8^e voorstel aldus gheseyt: Yder styflichaems swaerheyt is so veel lichter int water dan inde locht, als de swaerheyt des waters met hem euegroot.  Waer uyt ymant sulcken veruolgh mocht willen maken:

Yder styflichaems swaerheyt is so veel lichter int quicksiluer dan int water, als de swaerheyt des quicksiluers met hem euegroot.  Ofte aldus:
Yder styflichaems swaerheyt is so veel lichter int water dan inde olie, als de swaerheyt des waters met hem euegroot.  ende soo met dierghelicke.
Welck nootlick veruolgh, de saeck eenuoudichlick anghesien, d'eruaring teghen schijnt, want een pont loot en sal na de ghemeene ghebruyck van wegen, int water niet so veel lichter sijn dan in de olie, als de swaerheyt des waters met hem euegroot, maer alleenlick soo veel lichter, als t'verschil tweer lichamen van water en olie met dat voornomde loot euegroot. Doch den grondt dieper inghesien, ende d'ander parich ghestelt {Ceteris paribus.}, so bestaet alles in d'uyterste volmaectheyt.
Om t'welck te bewysen, so is t'anmercken, dat inde I^e begheerte der beghinselen des Waterwichts versocht is, Der lichamen ghewicht inde locht eyghen ghenoemt te worden, ende in de 5^e begheerte, T'vlacvat vol waters uytghegoten siinde, ledich te blijuen, dat is vol lochts te wesen duer de 11^e bepaling, daerom ghenomen dat de twee middelen quicsiluer en water sijn, alwaer nu water inde plaets des lochts ghestelt is, ende datmen hier sghelijcx begheere, Der lichamen ghewicht int water eyghen ghenoemt te worden.  Oock, T'vlacvat vol quicsiluers uytghegoten siinde, vol waters te blijuen, so is t'voornomde voorstel (Yder stijflichaems swaerheyt is soo veel lichter int quicksiluer dan int water, als de swaerheyt des quicksiluers met hem euegroot) waerachtich.
Om t'welck duer ghelijcknis noch opentlicker te verclaren, so neemt dat een man gantsch onder t'water sy, aldaer by hem hebbende quicsiluer, gout, met een waegh, ende houdende t'water als voor locht: Ick seg dattet gaudt aldaer so veel lichter sal sijn int quicsiluer dan int water, als de swaerheyt des quicsiluers mettet gaudt euegroot: t'welck openbaer is. Tis wel waer dat soomen naem, Der lichamen ghewicht int ydel eyghen ghenoemt te worden, soot in eenvoudich ansien oock is, men soude naer sulcke eyghenheyt mueghen segghen, Yder stijflichaems swaerheyt is soo veel lichter int water dan int ydel, als de swaerheyt des waters met hem euegroot.  Maer anghemerct d'omstaende, te weten dat ons ghemeene daetlicke weghinghen (naer welcke de Spiegheling {Theoria.} altijt opsicht behoort te nemen) niet int ydel en gheschien, maer inde locht, soo ist beter na d'eerste wyse, der lichamen eyghenwicht inde locht te stellen; Int ansien van welcken, t'boueschreuen 8^e voorstel met dieder uytvolghen, in haer uyterste volcommenheyt sijn, soo wy voorghenomen hadden te verclaren.

T' E I N D E   D E S   A N H A N G S.