D E N B V R G M E E S T E R S

E N D E R E G I E R D E R S D E R

S T A D T N V R R E N B E R G

V E E L G H E L V C X.

H E L I I C T onnutte cost waer, een groote stercke grondt te legghen, die een svvaer ghesticht draghen can, sonder eintlick eenich gebau daerop te vvillen brenghen; Alsoo is de spiegheling {Theoria.} inde beghinselen der consten verloren arbeydt, daer t'einde totte daet {Effectum.} niet en strect. Ghelijck oock na de natuerlicke oirden, dien grondt voor t'oppergebau gaedt, alsoo dese spiegheling voor huer daet.

Dit soo sijnde, ende vooren beschreuen hebbende de Beghinselen der Weeghconst, soo ist vouglick de W E E G H D A E T {Praxis.} te volghen; Oock my niet onbetamelick, de selue an ulieder E. Heeren toe te eyghenen, ende dat om drie besonder redenen:

D'eerste, dat haer voorstellen {Propositiones.} niet alleen onghehoort, maer oock nut sijn.

[ 4 ]

D'ander, dat haer voordering van nerghens merckelicker te vervvachten en scheen, dan vande ghene daer de Consten inde grootste acht sijn, vvaer af niet alleen en ghetuyghen de schriften veler gheleerden, maer oock selfs u ondersatens constighe daden {Effecta.}, verspreydt in allen houcken des vveerelts.

De laetste ende voornaemste, dat ick my duer sulcx toecommende voorthelpers hoopte te bereyden, tot seker daden mijns voornemens;
Met vvelcke eindelicke meining hier eindende, vvensch V.H. alle voorspoet ende vvelvaren.

Vyt Leyden in Oogstmaendt des 1586^e. Iaers.

[ 5 ]

A N D E N L E S E R.

V A N T in ettelicke voorstellen {Propositiones} der Weeghdaet ghehandelt sal worden vande roerselen der lichamen, soo heeft my goet ghedocht, eer wy tot de saeck commen, den Leser van dies wat te verclaren. Te weten dat de Weeghconst ons alleenlick leert, het roerende ter euelstaltwichticheyt brenghen mettet teroeren.
Angaende t'ghewicht ofte de macht, die t'roerende bouen dien noch behouft, om het teroeren ter roerlicke daet te crygen (welck ghewicht ofte macht, ouerwinnen moet des teroeren beletsel, dat in yder teroeren onscheydelicke ancleuing {Inseparabile accidens.} is) de Weeghconst en leert dat ghewicht ofte die macht niet Wisconstlick {Mathematicè.} vinden, d'oirsaeck is dattet een gheroerde ende siin beletsel niet euerednich {Proportionalis.} en is mettet ander gheroerde ende siin beletsel.

Maer op dat den sin van desen duer ghelijcknis opentlicker verstaen worde, soo laet by voorbeelt een waghen bekender swaerheyt, te trecken siin op een berch ofte hoochde bekender steylheyt; Ick seg dat de Weeghdaet leert, soo duer het 4^e voorbeelt des 9^en voorstels blijcken sal, hoe groote macht met die waghen euestaltwichtich, ofte euemachtich sal staen, sonder t'ansien roersel met siin belet, als assen teghen de bussen, rayers teghen de straet, waghen teghen de locht, etc. welcke macht des beletsels de Weeghconst niet en leert vinden, om dat sulcke beletselen ende haer gheroerden in gheen everedenheyt en bestaen,
so wy hier souden connen bethoonen, weerleghende de strijtredens {Argumenta.} vande ghene die in vallende swaerheden de contrarie meinen, ten waer ons voornemen is, in dese Weeghconst alleenlick met de leering voort te varen, ende d'oude dwalinghen der wichtighe ghedaenten elders te verworpen.

[ 6 ]

Merct oock dat dese kennis der euestaltwichticheyt tot de saeck ghenouch doet, want ligghende in elcke schael des waeghs eueveel ghewichts, ghelijck wy dan weten (hoewel de waegh oock haer belet des roersels heeft) dat tottet roersel der schalen luttel machts behouft, alsoo in allen anderen.

Dit is van t'belet des roersels tot dien einde gheseyt, op dat yemant duer de daet, de roerende macht altemet wat grooter beuindende, dan de gheroerde, niet en dencke sulcxs t'ghebreck der const te wesen, maer nootsaecklick, ouermidts, als vooren gheseyt is, t'roerende bouen de euestaltwichticheyt soo veel swaerder ofte machtigher moet siin, dan het teroeren, dattet sulck belet ouerwint.
Ten anderen, op dat niemant, die hem in sulcke schijn van eueredenheyt mocht betrouwen, bedroghen en worde, t'welck den ghenen alderlichtelicxt ghebuert, die t'valsche voor warachtich houden.

C O R T B E G R Y P.

{Argumentum.}

E S E Weeghdaet sal veruaten de werclicke vinding des swaerheyts middelplats, swaerheyts middellini, ende swaerheyts middelpunts: Voort de making des alderuolmaecsten Waeghs, met verclaring van etlicke huer ghedaenten. Oock den aldervolmaecsten Onsel. Wyder, de ghedaenten der steerten daermen ghewelt me doet: De ghedaenten der gedreghen ghewichten; Der Windassen; Der getrocken ghewichten; Ende des Almachtichs.

[ 7 ]

D E W E E G H D A E T

{Praxis artis Ponderaria.}

B E S C H R E V E N D V E R

S I M O N S T E V I N.

I. V O O R S T E L.
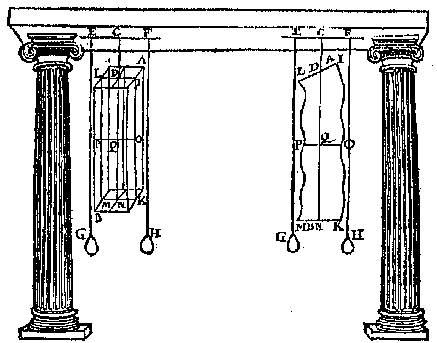
W E S E N D E ghegheuen een lichaem van form soot valt: Sijn swaerheyts middelplat, swaerheyts middellini, ende swaerheyts middelpunt werckelick te vinden.

I^e V O O R B E E L T.
T' G H E G H E V E N. Laet AB een lichaem sijn van form soot valt.
T' B E G H E E R D E. Wy moeten sijn swaerheyts middelplat, swaerheyts middellini, ende swaerheyts middelpunt werckelick vinden.
T' W E R C K. Men sal t'lichaem hanghen ande coorde CD, treckende duer t'opperste punt C, de rechte lini EF, hanghende uyt de selue lini twee fijne draen met hare ghewichtkens, als EG, FH, neuens het lichaem AB, ende t'plat veruaet tusschen de linien GE, FH, t'welck by ghedacht duer t'lichaem lijt, is des lichaems swaerheyts middelplat.

blok hangend aan koorde, tussen twee gewichtjes aan draden

[ 8 ]
Maer om sijn uyterste sijden op t'lichaem te teeckenen, men mach de draen EF, GH, bekriten, die ghespannen treckende, ende daer op teeckenende, ghelijck de Saghers haer boomen doen daer sy doorsaeght moeten sijn; Ick neme die linien te wesen IK, LM, teeckenende daer naer insghelijcx de linien LI, ende MK, t'plat LIKM, sal t'begheerde sijn.

Maer om nu de swaerheyts middellini te vinden, men sal t'lichaem noch hanghende an C, een weynich draeyen ende teeckenen een ander der ghelijcke swaerheyts middelplat, sniende t'voorgaende ick neem onder in N, ende bouen in D, ende haer ghemeene sne DN sal de begheerde sweerheyts middellini sijn:
Maer om t'swaerheyts middelpunt te vinden, men sal t'lichaem verhanghen inde dweersde, ick neem by t'punt O, ende vinden aldaer oock des lichaems swaerheyts middellini alsvooren, ick neem die te wesen OP, ende daer sy de lini DN sniit, als in Q, is t'begheerde swaerheyts middelpunt.

I I^e V O O R B E E L T.
T' G H E G H E V E N. Laet AB een lichaem sijn van form soot valt.
T' B E G H E E R D E. Wy moeten sijn swaerheyts middelplat, swaerheyts middellini, ende swaerheyts middelpunt werckelick vinden.
T'werck. Men sal t'lichaem AB legghen op eenighen scherpen cant als CD, dat vertreckende ter eender ende ander sijde, tot datmen sich bemercke de euestaltwichticheyt beyder sijden ghetroffen te hebben, t'welc ick neem te wesen in E, langwerpig voorwerp (boomstam?), op scherpe kant balancerend daerom t'plat rechthouckich op den sichteinder {Horizontem.} t'lichaem door E sniende, sal t'begheerde swaerheyts middelplat sijn. Ende een der ghelijcke plat t'voorgaende plat doorsniende, huer ghemeene sne sal swaerheyts middellini sijn. Ende soodanighen derde plat sniit die swaerheyts middellini in des lichaems swaerheyts middelpunt. Welcker bewys uyt de voorgaende openbaer is.
T' B E S L V Y T. Wesende dan ghegheuen een lichaem van form soot valt, wy hebben sijn swaerheyts middelplat, swaerheyts middellini, ende swaerheyts middelpunt werckelick gheuonden, naer de begheerde.

I I. V O O R S T E L.
E E N aldervolmaeckste waegh te maken.

T' W E R C K. Men sal eerst int middel des balcx AB, wiens tong ter behoirlicker plaets sy, teeckenen de lini CD onder t'middel der tong, rechthouckich op de canten des balcx,

[ 9 ]
ende vylen ofte weeren van d'een ende d'ander sijde soo veel stof, tot dat den balck (ligghende met de lini CD op eenighen scherpen cant) ouer beyden sijden met euen ermen euewichtich beuonden wort. Daer naer sal men trecken DE oock rechthouckich op de canten, ende legghen den balck op eenen scherpen stalen punt, ghenakende inde lini DE, souckende inde selue lini DE des balcx swaerheyts middellini, te weten den balck ter eender ende ander sijde vertreckende (welverstaende dat den stalen punt altijt inde lini DE blijue) tot datmen bemerckt de euewichticheyt ghetroffen te sijne, t'welck ic neem te wesen in F;

Daernaer gheteeckent een derghelijcke punt ouer d'ander sijde, de rechte lini door die twee punten sal de swaerheyts middellini des balcx sijn, beteeckenende t'scherp vanden dweersas, soo noem ick t'yserken daer op den balck int huysken rust.

[ 10 ]

Daer naer soo de schalen an dien balck met haecken moeten hanghen, man sal de plaetsen der ghenaecselen des balcx ende dier haecken als an A, B, alsoo stellen, dat sy ende t'scherp vanden dweersas in een rechte lini AFB commen te staen: verstaet wel t'voornomde woort Ghenaecselen, want wy spreken vande eyghen wesentlicke ghenaecselen der haecken teghen de stof des balcx. Maer soo t'ghene daer mede de schalen anden balck hanghen yet anders waer dan haecken, men sal op haer derghelijcke naecselen letten. T'welck ghedaen sijnde ende t'huysken t'sijnder plaets ghevoucht wesende, soodanighen waegh met alle euen ghewichten diemen in haer schalen soude mueghen legghen, sal, so lang den dweersas op haer scherpte rust, alle ghestalt houden diemen haer gheeft, door het 10 voorstel des I^en boucx vande beghinselen der Weeghconst.

Maer dat alsulcken waegh de aldervolmaecste sy, is openbaer door het I^e voorbeelt van het II^e [12e] voorstel des voornomden I^en boucx, alwaer bethoont is, dat wesende E vastpunt, wat ghewicht men an D soude moeten hanghen, om den as in ghegheuen gestalt te houden, maer so t'vastpunt aldaer had gheweest N, te weten het swaerheyts middelpunt des ghegheuens, daer en soude gheen ghewicht so cleen connen sijn Wisconstelick {Mathematicè.} sprekende, dat an D ghehangen, die sijde niet en soude doen gantselick neerdalen: T'selue is hier oock alsoo te verstaen, te weten dat tot d'een ofte d'ander deser euewichtigher deelen een seer cleen ghewicht gheleyt, die sijde sal stracx ten gronde sincken, daer sy van sommeghe ander waghen nau verroeren en soude.

Maer soot den Waeghmakers te moeylick viel die plaets van t'scherp des dweersas, metgaders de ghenaeckselen der haecken ende des balcx, altijt soo puntelick te treffen, sy mueghen t'ghene gheseyt is houden als voor hun wit, dat soo naer commende als sy willen oft connen; Ende so sy van t'volmaecste yet souden begheeren te verschillen, mueghen ghedachtich sijn t'naecsel der haecken ende des balcx lieuer te stellen een haerken beneden de rechte lini AB, dan daer bouen, want daer bouen ghestelt sijnde, alles keert omme duer het 8^e voorstel des I^en boucx, t'welck onbequaem is om te weghen; Ia t'ghene t'swaerste waer, soude altemet t'lichtste schijnen, voornamelick als den as duer de langde des balcx int beghin des weghens niet euewydich en waer vanden sichteinder {Horizonte.}, ouermits alles an die sijde keert daert eerst beghint.

Angaende dat de ermen des balcx euelanck moeten wesen, dat is kennelick, want soo d'eene een honderste deel des erms langher waer als d'ander, dat soude een bedriechlicke waegh sijn, ouermidts t'ghene euewichtich schene, soude een ten hondert verschillen; ende waer d'een een vyuentwintichste deel langer als d'ander, t'soude 4 ten hondert schillen, &c. Want ghelijck den langsten erm tot den cortsten, alsoo dit ghewicht tot dat, duer het I^e voorstel des I^en boucx.

[ 11 ]

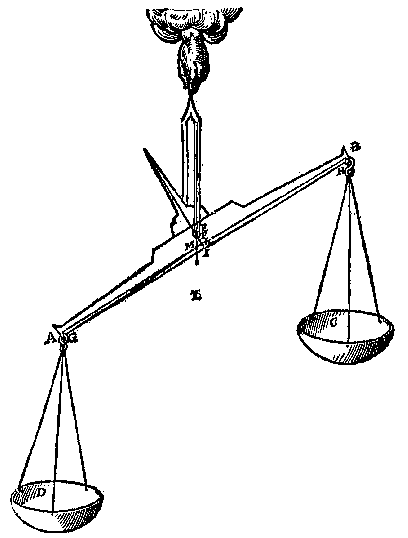
M E R C K T oock dat inde langste dunste ende lichtste balcken, t'grooste voordeel is om scherpelick te weghen. Want wesende twee euesware balcken maer d'een tweemael langher als d'ander, tis kennelick dat een once, aes oft wattet sy, ande langste tweemael meer ghewicht sal doen dan ande cortste duer t'voornoemde I^e voorstel.

T' B E S L V Y T. Wy hebben dan een aldervolmaeckste waegh ghemaeckt na t'voornemen.

I I I. V O O R S T E L.
W E S E N D E ghegheuen een waegh diens balck euewydich blijft vanden sichteinder {Horizonte.}: T'ghewicht te vinden dat in d'een schael gheleydt, den balck in begheerde ghestalt houde.

T' G H E B V E R T dickmael dat d'een waegh veel stegher gaet als d'ander, sonder datmen weet waer an het liecht, want t'scherp des dweersas is van d'een soo bequaem als van d'ander, ende inde reste en openbaert hem niet ooghenschynelicx daermen de reden duer bemercken can: Daerom sullen wy d'oirsaeck beschrijuen, bethoonende wat ghewicht men in d'een schael van soodanighen waegh sal moeten legghen op dat den balck blijue in begheerde ghestalt aldus:
T' G H E G H E V E N. Laet de waegh ABCD sulck sijn, dat alles vry hanghende, den balck soude eintlick euewydich vanden sichteinder rusten, ende E sy t'scherp vanden dweersas.
T' B E G H E E R D E. Wy moeten inde schael D eenich ghewicht legghen, sulcx, dat den balck in die ghegheuen ghestalt blijue.
T' W E R C K. Men sal t'huysken ende de schalen met haren coorden ende haecken afdoen, vindende des balcx met de tong daeran swaerheyts middellini, euewydich mettet scherp vanden dweersas E, door het I^e voorstel deses boucx, t'welck ick neem F te sijne, daer naer salmen trecken een lini tusschen de plaetsen der naecselen des balcx ende der haecken vande schalen, welcke sy GH, wiens middel sy I: 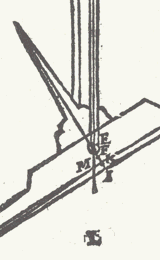balans, detail bij ophangpunt

Daernaer salmen FI deelen, alsoo dat de stucken inde reden sijn van t'ghewicht des balcx met de tong, welcke sy 1 lb, tot de schalen met haer coorden ende haecken, welcke ick neem te weghen oock 1 lb, daerom ghedeelt FI, int middel K, soo sal K t'punt sijn daer an de ghegheuen waegh alle ghestalt soude houden diemen haer gheeft; Daernaer ghetrocken de lini KG, ende de hanghende duer E als EL, sniende KG in M; Ick seg dat een ghewicht in sulcken reden tot 2 lb (te weten 1 lb voor den balck, ende 1 lb voor de schalen, t'samen 2 lb) als MK tot MG, t'begheerde sal sijn, t'welck gheleydt inde schael D, de waegh in die standt sal houden.

[ Fig. toegevoegd. ]

[ 12 ]

Ghenomen dan dat MK het vijuentwintichste deel waer van MG, so sal het vijuentwintichste deel van 2 lb de waegh in die ghestalt houden, waer af t'bewys openbaer is duer het 12^e voorstel des I^en boucx, maer wy sullender hier om meerder claerheyt, noch een weynich af segghen.

[ 13 ]

T' B E W Y S. Anghesien K swaerheyts middelpunt beteeckent des ghegheuens, so sal de hanghende {Perpendicularis.} duer K, des selfden swaerheyts middellini wesen, ende de hanghende duer G, is swaerheyts middellini des toegheleyden inde schael D, daerom de lini KG, tusschen die twee swaerheyts middellinien, is der seluer weeghconstighen balck; Maer sy is ghedeelt in M, also dat den erm MG, sulcken reden heeft tot den erm MK, als diens swaerheyt tot desens; De hanghende dan duer M, is swaerheyts middellini ofte handtaef des heels, ende veruolghens den balck blijft in die ghestalt, t'welck wy bewysen moesten.
T' B E S L V Y T. Wesende dan ghegheuen een waegh, diens balck euewydich blijft vanden sichteinder, wy hebben t'ghewicht gheuonden, dat in d'een schael gheleyt, den balck in begheerde ghestalt houdt, na t'voornemen.

I I I I. V O O R S T E L.
W E S E N D E ghegheuen een balck welcke met haer schalen euewydich blijft vanden sichteinder {Horizonte.}, maer sonder schalen op t'scherp vanden dweersas niet rusten en can: Te vinden hoe sware schalen men daer an hanghen sal, op dat den balck alle ghestalt houde diemen haer gheeft.

T' G H E B V E R T sommighe balcken, dat sy sonder schalen op t'scherp van haren dweersas niet rusten en connen, maer wel de schalen daer an hanghende, welcker dinghen oirsaken wy duer de daet versoucken moeten.
T' G H E G H E V E N. Laet AB een balck wesen van ghedaente deses voorstels, wiens dweersassens scherp sy C.
T' B E G H E E R D E. Wy moeten an desen balck twee schalen vinden (daerby men verstaen sal schalen met haer coorden en haecken) van sulck ghewicht, dat sy den balck alle ghestalt doen houden diemen haer gheeft.
T' W E R C K. Men sal vinden des balcx met de tong daer an swaerheyts middellini, euewydich van t'scherp des dweersas C duer het I^e voorstel deses boucx, welcke sy D, bouen C, want in C noch onder C en salse niet vallen, ouermidts den balck op C, duer t'ghestelde niet rusten en can, noch min onder C. Daer naer salmen trecken de lini EF tusschen de plaetsen der ghenaecselen des balcx, ende de haecken der schalen, de selue sal nootsaecklick vallen onder C, want vielse daer in, of daer bouen, gheen schalen hoe swaer sy waren, en souden den balck alle ghestalt connen doen houden diemen haer gaue, ofte euewydich doen blijuen vanden sichteinder. Daer naer gheteeckent G int middel van EF, men sal trecken de rechte lini DCG, ende ghelijck dan CD, tot CG, alsoo moet tghewicht der begheerde schalen HI sijn, tot t'ghewicht des balcx;

[ 14 ]

ick neme dat CD euen sy an CG, t'ghewicht dan der schalen sal euen moeten wesen an t'ghewicht des balcx, waer af t'bewys Wisconstlick {Mathematicè.} ghedaen is int 10^e voorstel des I^en boucx, daer toe wy hier tot meerder claerheyt noch een weynich sullen segghen.

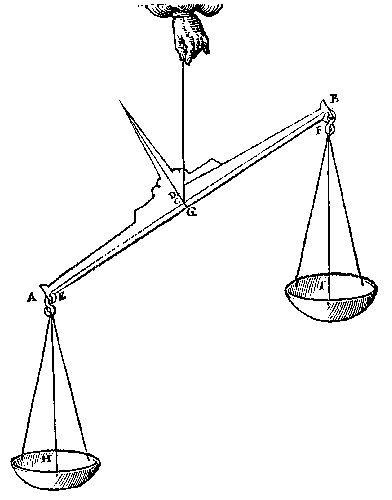
T' B E W Y S. De hanghende {Perpendicularis.} duer D, is swaerheyts middellini des balcx ter eender sijden, ende de hanghende door G is swaerheyts middellini der schalen ter ander sijde; GD dan is Weegconstighen balck:

[ 15 ]

Maer ghelijck den erm CD tot den erm CG, also dese swaerheyt tot die duer t'ghestelde', het houdt dan op C alle ghestalt diemen hem gheeft, t'welck wy bewysen moesten.
T' B E S L V Y T. Wesende dan ghegheuen een balck, welcke met haer schalen euewydich blijft vanden sichteinder, maer sonder schalen op t'scerp vanden dweersas niet rusten en can; wy hebben gheuonden hoe sware schalen men daer an hanghen sal, op dat de balck alle ghestalt houde diemen haer gheeft, naer de begheerte.

M E R C K T.
Tis openbaer, dat by alsien de schalen yet swaerder waren dan bouen gheseyt is, ofte dat in haer eenighe euen swaerheden gheleyt wierden, soo en soude den balck dan niet alle ghestalt houden diemen hem gheeft, maer euewydich blijuen vanden sichteinder, daerom en sijn sulcke waghen niet de volmaeckste.

Home | Simon Stevin | Weeghdaet | Begin, Voorstel 1 - 4 (top) | 5 - 7