Home | Stevin | Weeghdaet | Woordenlijst

Overzicht , Inleiding , zwaartepunt , werklieden , peert , snaphaen , steerten , Almachtich , Noten

---

Stevins Weeghdaet De Weeghdaet is uitgegeven in 1586, samen met De Beghinselen der Weeghconst, De Beghinselen des Waterwichts, en een 'Anhang'. Er zijn 43 bladzijden, hier verdeeld in vier stukken: Begin met:  Opdracht, Anden Leser, Cortbegryp, en Voorstel 1 t/m 4:  Swaerheyts middelplat, -lini, en -punt, Waegh Voorstel 5 t/m 7:  Onsel, Scheefwaeg, Steerten daermen ghewelt me doet Voorstel 8, 9:  Ghedreghen swaerheden, Windassen en Ghetrocken swaerheden Voorstel 10:  Almachtich, Ghebruyck, Cracht, Keeren des crucx, Verclaring. In 1605 kwam er nog een Byvough, met andere praktische toepassingen van de weegkunde. Een eerdere was het braadspit, ook als uurwerk en wieger te gebruiken. Zie deel 1 van Principal Works voor een facsimile van De Weeghdaet.   Origineel bij Google (UvA). Ander ex. (BSB) heeft het gedicht 'Om de weeghconst' van Jan de Groot, en de 'Uytspraeck' over de taal; dan Weeghdaet, Weeghconst, Waterwicht. Inleiding De Weeghdaet is opgedragen aan de burgemeesters van Neurenberg, een stad die in de 15e eeuw, onder invloed van de geleerde Regiomontanus, een belangrijk centrum geworden was voor de wiskundige wetenschappen. Boekdrukkers en instrumentmakers verspreidden de kennis over Europa*). In de opdracht vergelijkt Stevin zijn Beghinselen der Weeghconst met een "stercke grondt" waarop nu een "ghebau" gezet gaat worden. Spiegeling en daad kunnen niet los van elkaar staan. Uit de onderwerpen blijkt: een 'weeghdaet' is niet alleen een meting van de zwaarte van iets, met een "waegh" (balans) of "onsel" (ongelijkarmige balans met weeghaak) 1. Het gaat ook over tillen en torsen, duwen en trekken, zoals de tekeningen duidelijk laten zien. Uitgangspunt is hierbij het eerste voorstel uit het eerste boek der Beghinselen, de 'hefboomwet': Wesende twee evestaltwichtighe swaerheden, de swaerste heeft sulcken reden tot de lichtste, als den langsten erm tot den cortsten. In onze woorden: als aan een hefboom twee gewichten elkaar in evenwicht houden is de verhouding van zwaarste tot lichtste gelijk aan die van langste arm tot kortste. Maar de praktijk is nog wat anders dan de theorie, er is altijd wrijving (beletsel). Om iets op gang te krijgen is er meer nodig dan voor evenwicht. In Anden Leser staat het zo: dat de Weeghconst ons alleenlick leert, het roerende ter evestaltwichticheyt brenghen mettet teroeren. Angaende t'ghewicht ofte de macht, die t'roerende boven dien noch behouft, om het teroeren ter roerlicke daet te crygen (welck ghewicht ofte macht, overwinnen moet des teroeren beletsel [...]) de Weeghconst en leert dat ghewicht ofte die macht niet Wisconstlick vinden, d'oirsaeck is dattet een gheroerde ende siin beletsel niet everednich en is mettet ander gheroerde ende siin beletsel. De extra-kracht valt niet te berekenen, want de wrijving is niet evenredig met het te bewegen voorwerp. Ook andere 'beghinselen' komen aan de orde. Stevin legt op heldere manier uit, vaak met tekeningen, hoe je ze toepast in praktische situaties.   *)  J. G. Doppelmayr, Historische Nachricht von den Nürnbergischen Mathematicis und Künstlern (1730). Zwaartepunt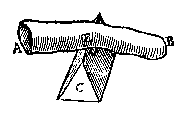 Het eerste voorstel gaat over de bepaling van het zwaartepunt. Om te weten wat je moet doen om dit "werckelick te vinden" (niet wiskundig, maar met echt werk) hoef je eigenlijk alleen maar naar de tekening te kijken. Heel anders dan de hooggeleerden van zijn tijd kon Stevin zich goed verplaatsen in de leefwereld van simpeler mensen, en met eenvoudige woorden in de eigen taal maakte hij de wereld van het denken voor hen toegankelijk: Laet AB een leere [ladder] wesen, op t'een einde swaerder als op t'ander soo sy ghemeenlick sijn, welcke ghedreghen moet worden van twee mannen, alsoo dat d'een soo veel ghewicht draghe als d'ander, dat is elck den helft [...] Men sal de leere op eenighen scherpen cant legghen, die vertreckende voorwaert ende achterwaert, tot datmen bemercke de euestaltwichticheyt ghetroffen te sijne, t'welck ick neem in E te wesen, ende sosy dicwils moet verdreghen sijn van d'een plaets ten anderen, men mach an E een kerfken stellen Hoe elk de helft van de ladder krijgt te dragen laat hij zien met tekeningen van het dragen op de schouder, of aan de hand. En dan veralgemeent hij: "yder lichaem", "ende dat de selue mannen eenen berch ofte hoochde opsteghen". Door deze bladzijden kan veler ervaring in het torsen van zware lasten verrijkt zijn (en worden) met inzicht. Werklieden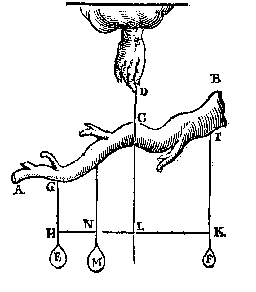 Omdat "veler wercklieden gheleghentheyt niet en is die voorstellen te leeren" laat Stevin ook zien hoe zij natuurkunde kunnen bedrijven in het vrije veld, zodat ze "wat ooghenschijnelicx saghen, waer duer sijt gheloofden": die mueghen nemen een rechten gheschickten, ofte crommen ongheschickten stock, soot valt [...] hanghende anden stock even ghewichten als E, F, alsoo dat [...] HL even sy an LK, den stock sal haer eerste stant houden [...] t'selve sal sy oock doen soomen E weerde, ende datmen anhinghe t'ghewicht M, dobbel an F, ende also dat LK oock dobbel sy an LN Aanwijzingen bij het maken van een balans ("waegh"): Maer soot den Waeghmakers te moeylick viel die plaets van t'scherp des dweersas, metgaders de ghenaeckselen der haecken ende des balcx, altijt soo puntelick te treffen, sy mueghen t'ghene gheseyt is houden als voor hun wit, dat soo naer commende als sy willen oft connen; Het woord 'wit' in de betekenis van 'doel' kennen we nog in 'doelwit'. Ende so sy van t'volmaecste yet souden begheeren te verschillen, mueghen ghedachtich sijn t'naecsel der haecken ende des balcx liever te stellen een haerken beneden de rechte lini AB, dan daer boven, want daer boven ghestelt sijnde, alles keert omme [...] De haken, waaraan de schalen hangen, kunnen de balk beter raken onder de horizontale lijn door het zwaartepunt; anders ontstaat een labiel geheel. Angaende dat de ermen des balcx evelanck moeten wesen, dat is kennelick, want soo d'eene een honderste deel des erms langher waer als d'ander, dat soude een bedriechlicke waegh sijn, overmidts t'ghene evewichtich schene, soude een ten hondert verschillen [...] 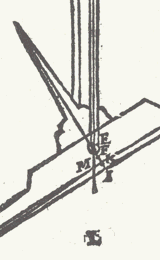T'ghebeurt dickmael dat d'een waegh veel stegher gaet als d'ander, sonder datmen weet waer an het liecht, want t'scherp des dweersas is van d'een soo bequaem als van d'ander, ende inde reste en openbaert hem niet ooghenschynelicx daermen de reden duer bemercken can: Daerom sullen wy d'oirsaeck beschrijven, bethoonende wat ghewicht men in d'een schael van soodanighen waegh sal moeten legghen op dat den balck blijve in begheerde ghestalt Afbeelding: TU Delft De ene balans gaat stugger dan de andere: er is meer gewicht nodig voor een zelfde uitslag. Het verband tussen gewicht en uitslag wordt als volgt gevonden: E is het ophangpunt van de balk, F het zwaartepunt van balk met 'tong' (wijzer), I het midden van de lijn tussen de ophangpunten van de schalen (links G), K het midden van FI (genomen dat de schalen met koorden en haken even zwaar zijn als balk met tong). Dan is K het punt waar de balans bij elke stand in evenwicht is, oftewel het zwaartepunt van het geheel. Als M het snijpunt is van KG met de vertikaal EL (L onderaan) geldt de verhouding: gewicht op linkerschaal : gewicht van balans = MK : MG. Paard Met het paard leeft Stevin mee, als hij voorrekent: hoe veel ghewichts een peert in een waghen ghespannen, meer treckt een hoochde op styghende, dan opt plat landt. [...] Daerom t'gareel oft riem oft sulcx alst waer, druckt t'peert soo stijf voor den borst L, als een pack van 500 lb op sijn rugghe duwen soude, ende dat (wel verstaende alst voortgaet) bouen het duytsel dattet lijdt op t'plat landt treckende. Een 'duytsel' is een ingedrukt merkteken, vergelijk: duit. De ervaring van de gewone man wordt verklaard met de theorie: als het paard de wagen trekt op het platte land is het bevorderlijk de 'strengen' niet horizontaal te doen, maar achter wat lager. Waarom is dat zo? op eenen oneffenen hobbelighen ende sandighen [wech], so voorderet de strijnghen achter wat leegher te doen dan vooren. T'welck den Hollantschen voerlien duer dervaring niet onbekent en is, diens waghens daer naer ghemackt sijnde, doen de strijnghen, langs t'zeestrant varende, ende in derghelijcke even harde weghen, achter hoogher, dan inde oneven ende sandighe. Reden is dese, dat wesende de strijnghen evewydich vanden sichteinder, so en sijnse niet evewydich met die oneven verhefselen, t'welck int overtrecken nootsakelick meerder last anbrengt, dan als de strijnghen achter leegher sijn Meer over het paard in de Byvough: de Toomprang.   De afbeelding werd kennelijk gebruikt voor de titelpagina van G. van Aelst, Theoremata mathematica. Scientiae staticae, 1624.  [>] De naam Stevinus komt daar voor (met eronder de 'clootcrans') in de figuur bij nr. 7. Vergelijk ook de voorlaatste figuur (nr. 19) met die van Weeghdaet, p. 25: 2 mannen die een last een helling op dragen. De afbeelding staat gespiegeld in: Georg Philipp Harsdörffer, Delitiae philosophicae et mathematicae ... Erquickstunden, 3, Neurenberg 1653, p. 396. Snaphaan Stevins formuleringen doen ons wel eens komisch aan, juist ook bij zijn heel serieuze uitleg. Maar wij missen waarschijnlijk vaak de momenten waarop hij zelf zat te grinniken bij het schrijven. Humor is bij hem zeker aanwezig, maar dan op een onderkoelde manier. Een voorbeeld is te vinden op blz 21, waar eerst de krachten berekend worden bij het dragen van een lans op de schouder:

Maer so den man A waer een Snaphaen, met een ghesnapten haen I an K hanghende, weghende 3 lb, [...] tis kennelick dat den buyt sijn handt van 9 lb meer verswaren [...] soude. Het woord 'snaphaan' betekende: rover 2, maar Stevin neemt het letterlijk: de man heeft een haan 'gesnapt'. De buit voelt lekker zwaar, maar dat komt door de grote afstand tot zijn schouder.   Devreese & Vanden Berghe (2003, p. 176): de tekening is in spiegelbeeld, sabel rechts i.p.v. links. Nooit maakt Stevin iemand anders belachelijk, niet als het gaat over de "aerbeyders", en ook niet als hij met ervaringen uit de praktijk enkele dwaze uitspraken van geleerden bestrijdt. Oude dwalingen worden in de Anhang verworpen op een sobere manier: inde plaets van veel besonder dwalinghen, alleen haer ghemeene oirspronck Over de "strijtredens" van de geleerden spreekt hij zijn "mishaghen" uit. Steerten Bij het gebruik van hefbomen, de "steerten daermen ghewelt mede doet", is het handig als je snapt hoe het werkt: Siende de menschen datmen met langher steerten een merckelicker grooter ghewelt dede dan met de corter, sy hebben veel ghemeene reetschappen tot hueren grooten dienste ende voordele daer duer ter daet ghebrocht: Maer want sulcx alleen gheschiede duer ervaringhen, ende niet duer grondelicke kennis der everedenheyt {Proportionis.} in huer bestaende, soo en sijn veel groote nieuwe wercken dickmael niet wel gheluckt, tot groote schade der Makers, ende verachtering des voornemens. Stevin laat zien hoe je een nieuwe situatie in verband brengt met een bekende, en hij geeft weer zo'n tip voor de werklieden die het echt willen snappen: maak zelf een tekening! Wy hebben tot hier de ghedaente verclaert alwaer twee steerten sijn, over elcke sijde des vastpunts een; Wy sullen nu een voorbeelt gheven vanden steert alleenlick over een sijde.   T' G H E G H E V E N.   Laet AB een steert sijn, vast an t'einde A, de rest verroerlick, [...]   De vraegh is hoe sterck men an B sal moeten heffen om den steert met t'ghewicht F op te lichten.

T' W E R C K.   [ ... ]   Men sal dan an B soo grooten ghewelt moeten doen om met de reste evestaltwichtich te sijn, als oftmen 280 lb ophielde. 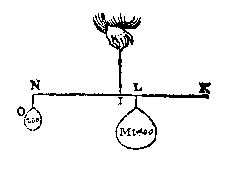  Maer soo den Wegher de voornoemde rekening wilde maken door naeckter kennis des grondts, hy mach sich selfs Weeghconstighe formen beschrijven, ghelijck den Meter {Geometricus.} om t'verstercken des ghedachts, hem Meetconstighe voorstelt, aldus: Ick treck de lini IK, beteeckenende den steert AB van 10 voeten, ende overmits AH twee voeten was, ende H swaerheyts middelpunt, ick teecken L, alsoo dat IL beteecken 2 voeten van IK 10, hanghende M 1400 lb an L, treckende daer naer IN even an IK, ende houdende I voor vastpunt, ick sie wat ghewicht an N sal moeten hanghen, op dattet met M evestaltwichtich sy [...] Maer O doet so veel an N dalende, als t'selve ghewicht an K heffende En dan komt hij voor de 'steert' AB weer uit op: hy moet 280 lb lichten an B, om met de rest evestaltwichtich te wesen. Der ghelijcke formen mach den Wegher in alle werckelicke voorbeelden sijn selven altijt voorstellen, welcke hier om cortheyt achterghelaten sijn. Almachtich Als Stevin zijn nieuwe krachtwerktuig het 'Almachtich' gaat beschrijven blijkt dat hij de klassieken kent, maar ook dat hij op de hoogte is van wat pas verschenen is: P L V T A R C H V S  ende ander, schrijven dat Hiero Koninck van Sicilien, dede bauwen een schip van uytnemender grootheyt ende constigher form, om te schencken an Ptolemeus Koninck van Egypten; T'welck, doent [toen het] volmaeckt was, de burgheren van Syracusa om sijn swaerheyt in zee niet crijghen en conden, maer doen Archimedes daer an ghestelt had sijn reetschap die de Griecken Charistion noemen, Hiero heeft het daer duer selfs alleen metter handt vertrocken. Dese Charistion (naer de form die Iacques Besson daer af heeft laten uytgaen, ghevonden inde bouckamer {Bibliotheca.} des Kuenincx van Vranckrijck) had assen met vijsen, draeyende inde canten van ettelicke raeyers: Een werck voorwaer weerdich sijn eeuwighe ghedachtnis, ende soudent hier beschriven overmidts wy tot sulcke stof ghecommen sijn, ten waer wy in die plaets stelden  T A L M A C H T I C H  (reetschap die wy om sijne overgroote macht dien naem gheven) tot sulcke daet bequamer, te weten Stercker gheduerigher werck; Van minder cost; Duer t'welckmen op corter tijt meer afveerdicht; Ende (ghelijck de Charistion) van oneindelicke cracht, machtelick welverstaende, niet daetlick {Potentia non actu.}. Dit is uit 1586, in de latere uitgave van de 'Weeghconst', van 1605, is de formulering iets anders 3. 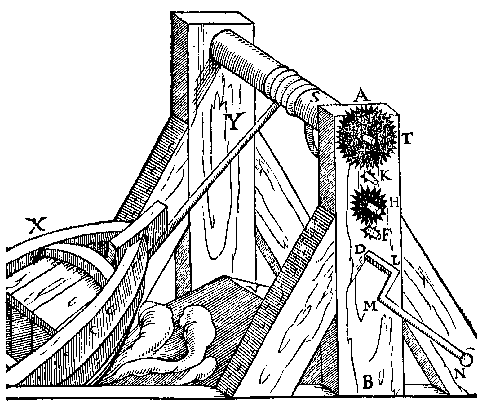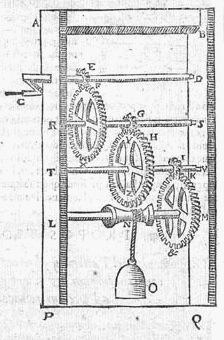Dan volgt een uitvoerige beschrijving, en een gebruiksvoorbeeld: Maer om de ghebruyck dese Almachtichs te verclaren, wy sullen een voorbeelt gheven daer alle d'ander ghenouch duer sullen bekent sijn, te weten van schepen daer mede over dammen of dijcken te trecken, want dat den cleynsten dienst niet en schijnt, die dese landen hier in ghedaen mach worden, voornamelick Hollandt. Een schip werd toen over een dam getrokken met een windas. Die had een vaste overbrengingsverhouding. Het Almachtich is beter, omdat de tandwielen makkelijk zijn in te stellen op een grote of kleine kracht: want om een cleyne lichte schuyt, ghebruycktmen duer windassen, t'ghene een veel grooter cracht vermach, t'welck den tijdt langher doet anloopen. Om een licht schuitje over de dam te trekken gebruikt men met een windas iets dat een veel grotere kracht vermag, en dat duurt te lang.

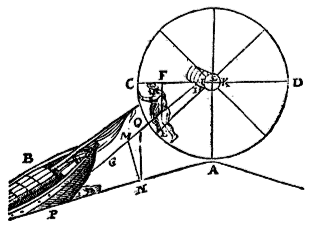
Berekening: De man weegt 150 pond, en kan (onder F, verhouding 1 : 6) een kracht van 900 pond aan het touw geven. Die kracht wordt voorgesteld door het lijnstukje OM, als NM loodrecht op de helling is, en ON het gewicht van het schip. OM : ON = 1 : 3, dus het schip weegt 2700 pond (3/4 last). (Dit geldt alleen bij evenwicht, zonder wrijving.)   Een dergelijke figuur staat bij een vraagstuk in: Dirck Rembrantz van Nierop, Mathematische calculatie (1659), p. 164, met dezelfde (nu wel rechthoekig getekende) driehoek MNO. Als het schip te zwaar is voor de windas kan het beschadigd worden, door een groot aantal ('menichte') mensen of paarden die met horten en stoten het schip van zijn plaats krijgen: Maer is het tetreckenwicht swaerder dan daer duer bequamelick can ghedaen worden, soo moetmen daer toe nemen groote menichte van menschen ofte peerden, welcke met grooten arbeydt altemet voortgaen, altemet stilstaen, ende daer duer den tijt verlanghen; Ia boven dien de schepen seer beschadighen, want een der grootste die over den Leydtschen Dam*) ghetrocken worden van derthien oft veerthien last, behouft twintich menschen die inde raeyers gaen, welcke dickwils naer eenen stillestandt alt samen neerdalen, ende met eenen grooten gheweldighen hurt de schepen seer quetsen, t'welck duer t'Almachtich niet gheschien en can, overmidts t'schip altijdt eenvaerdelick ende sachtkens voortcomt.   *)  Afb. Iven Besout 1755 (geen overtoom, maar een verlaat, zie 'Schuttejagers'); zie ook Kabinet van Nederlandsche en Kleefsche Outheden, 3 (1732), p. 85 (Abr. Rademaker, prent 107 in ed. 1725: geen overtoom te zien). C.G.D. de Wilt, Delflands kaarten belicht (2000), p. 105. Damwachters, 'De Leytsche Dam'. Het Almachtich wordt verder behandeld in hoofdstukken met berekening van verhoudingen, en van benodigde tijd: Reden dieder is vande keeren des krucx tot de keeren des as [p. 37]. Reden vande cracht des draeyers ande cruc, tot het ghetrockenwicht als t'schip X [p. 38]. Vande menichte der keeren des crucx om t'schip over den dam te winden: Ende vanden tijdt die de aerbeyders behouven [p. 39]. Aan het eind van de Weeghdaet moet Stevin toch nog even 'spieghelen'. In een hoofdstuk "Verclaring van t'ghene vooren belooft is" fantaseert hij over de "oneindelicke cracht" van zijn hijsinstrument. Eerst vergelijkt hij: Maer om vande oneindelicke cracht te segghen, het is te weten datmen met de kruc [...] soo veel vermach alsmen soude met een windas diens radts middellini van 324 voeten waer [...] Maer de meeste diemen maeckt en schijnen de 30 voeten niet te bereycken, waer uyt opentlick blijckt hoe veel t'Almachtich meer vermach dan de windassen, wel is waer dat eenen gaende int radt eens windas, sijn ghewelt met minder aerbeydt doet, maer ghemerckt de voorgaende omstaende, ten is niet het nutste. Terloops wordt dus toch nog een voordeel vermeld van de windas met looprad: je laat de zwaartekracht het werk doen (maar je moet wel steeds klimmen).

Laet ons nu ande kruck (stekende anden leeghsten as van soodanighen Almachtich) een kindeken stellen, wat meer macht daer an doende dan een hanghende pondt, t'selve soude op den hoochsten as een ghewicht winden van 100000000000000000000000000000000 lb (maer ghedenckt dat dien hoochsten as op den eersten dach gheen heelen keeren doen en soude) dat is een ghewicht swaerder dan vierduysent mael t'eertrijck met al datter in is

1. De 'onsel' of unster komt als 'ontser wicht' voor in Roemer Visscher, Sinnepoppen (1614), LIX: een handig weeginstrument, maar niet zo nauwkeurig en "selden ghebruyckt in dinghen te wegen van groote waerdyen: maer meest in't ontlossen van Waghens en Muylen, om de vracht aen den Wagenaer of Muyletier te betalen."
   Meer interessante afbeeldingen zijn daar te vinden, zoals op p. 3: ploeg, p. 6: kompas, 16: heugel, 19: sluizen, 29: letterslot, 83: windas met tredmolen ("raeyers daer menschen in gaen", Weeghdaet, p. 28-29), 121: heien, 141: zee-astrolabium, 161: balans.   «

   
   

2. Erasmus gebruikte al het woord 'snaphaan' in zijn Samenspraak 'Rijke bedelaars', maar dan in het Latijn (snaphanus).
   Colloquium XXX, Ptôchoploúsioi (Franciscani), in Familiarum colloquiorum opus (1526), p. 305.

   Olim Monachi nihil aliud eramus quam purior pars laicorum. Et hoc intererat inter Monachum et alium laicum, quod nunc interest inter frugalem et probum virum suis manibus alentem familiam, et inter Snaphanum ex praedationum reditu iactantem sese.

   De XXXV t'Samen-sprekinge, Ptochoplousii Franciscani, De kap maekt de man niet (1664), p. 406:

   Eertijts en waren wy Moniken anders niet dan het suyverste deel der Leken, en dit onderscheyt was daer tussen een Monik en een ander Leek, dat hedensdaegs is tussen een gematigd' vroom Man, die met zijn handen zijn huysgesin onderhoud, en tussen een opsnapper, die hem van de inkomst zijner roverijen beroemt.

   Zie:  A. H. Wesseling, 'Dutch Proverbs and Expressions in Erasmus' Adages, Colloquies, and Letters', in Renaissance Quarterly, 2002; 55 (1), 81-147.  En eventueel het daar genoemde pamflet tegen roverbaronnen, met de titel: Schnaphan (1523) — "fürt eyn armes reüter leben" (p. 1); het gaat om Franz von Sickingen (p. 2).   «

   
   

3. In 1605 kwam de 'Weeghconst' in de 'Wisconstighe Ghedachtenissen' voor prins Maurits, met een Byvough. De spelling is iets gemoderniseerd, maar de tekst is vrijwel gelijk. Wat opvalt is een verandering in het voorstel over het Almachtige, waarvan 1e en 2e versie luiden:

   T' M A E C K S E L  ende de eyghenschappen des Almachtichs te verclaren.

   Ghedaenten en omstandigen der oneyndelicke crachten te verclaren.

   Het Almachtig werktuig was kennelijk niet zo'n doorslaand succes geworden als Stevin gehoopt had. De inleiding verwijst nu naar een tekening ervan, als een voorbeeld om krachten uit te leggen (p. 112):

   De menschen maecken verscheyden reetschappen om cracht met te doen, waer in sy de ghewelt altijt connen vermeerderen sonder eynde, welcke wy daerom int ghemeen oneyndelicke crachten noemen.
   Om te verclaren de ghedaenten en omstandighen der selfde; Als wat doende ghewelt in sulcken voorghestelden tuych evestaltwichtich sal sijn teghen het vertreckelick ghewicht: Hoe langhe tijt datter sal behouven om t'selve een seker verheyt te beweghen, en dierghelijcke, daer toe sal ick een form teyckenen van eenvoudighe gedaente, doch sulcx dat icker mijn voorghenomen verclaring bequamelick me sal connen te kennen gheven, eerst wat geseyt hebbende van Archimedes oneyndelicke cracht, daer Plutarchus en ander af schrijven. Te weten dat Hiero [...]

   En dan volgt wat in de eerste versie op blz 34 stond.
   De zin over het Charistion in het boek van Besson is ook veranderd:

   [...] inde bouckamer {Bibliotheca.} des Kuenincx van Vranckrijck)  had assen met vijsen, draeyende inde canten van ettelicke raeyers:

   [...] inde bouckas des Coninx van Vranckrijk)  hadde assen met oneyndelicke schrouven:

Hoe het schip van Hiero in zee getrokken werd volgens Besson (1572/8), pl. 54.
Archimedes werkt hier "cum opera trispasti", m.b.v. een toestel met 3 katrollen.
(Een 'oneindige schroef' staat op pl. 53.)

Verder wordt de naam 'Almachtich' gebruikt zoals eerst. Maar wel consequent:

Wy hebben hier vooren int t'beghin deses voorstels belooft, dattet Almachtich soude sijn stercker werck [...]

Ick heb hier vooren in t'begin deses voorstels gheseyt dat dese oneyndelicke cracht mijns bedunckens soude sijn stercker werck [...]

Stevin is nu ouder en wijzer: de belofte van "stercker werck" is er niet meer!
Het Almachtige was misschien de 'inventie' waarop in 1584 octrooi verleend werd, om schepen "over dammen te voeren" (zie Principal Works deel 5, blz 11, 26). Kennelijk was een praktische uitvoering met de bestaande technieken nog niet mogelijk.
  Besson's afbeelding komt voor in:
Wolfgang Lefèvre, Jürgen Renn, Urs Schoepflin, The power of images in early modern science, 2003.

  Over het woord 'charistion' zie:
-  E.J. Dijksterhuis, 'Het leven van Archimedes', in Euclides, 11-4 (1934/35) 171-173. Over het schip: p. 168-170.
-  René Dugas, A history of mechanics (1955/2012), p. 37: "Liber Charastonis is the Latin version of an arabic text due to the geometer Thâbit ibn Kurrah (836-901). The original greek version remains unknown, and the question of whether Karaston (in Arabic - karstûn) refers merely to the roman balance or to the name of the greek geometer Charistion (a contemporary of Philon of Byzantium in the IInd Century B.C.) has been the subject of much scholarly debate."
-  F. de Gandt, p. 111 in J. Barnes e.a. (ed.), Science and Speculation (1982/2005): het is niet zeker of het woord 'charistion' komt van het Armeens-Perzische 'qarastun', en de Griekse meetkundige Charistion is imaginair.
-  Jessica Wolfe, Humanism, machinery, and Renaissance literature (2004), p. 54: 'grace machine', van het Griekse 'charis' - welgevallen (zoals in charisma). Misschien was het gewoon de hefboom (Engl. lever).
-  M. Abattouy, 'An Arabic science of weights', in A shared legacy (Barcelona 2008), p. 86: "qarastun or steelyard" (unster).
Principal works 1, p. 355, 371. Pierre Duhem, The Origins of Statics (1991), o. a. p. 67 (Fr. 1905).
  «

4. Meer informatie over Stevins grote voorbeeld: Archimedes Home Page.
   Het was een lumineus idee, dat iemand de Aarde zou kunnen verplaatsen als hij maar een vast punt had om op te staan. Het staat in beeld gebracht op de titelpagina van Guidobaldo del Monte's Mechanicorum Liber (1577; Engl.), en dit beeld is het logo geworden van het 'Archimedes Project', dat zoveel werk van oude mechanica-meesters toegankelijk maakt. Al in een vroeg stadium werd bij dit project de 'Weegconst' van Stevin gedigitaliseerd. De 'Weegdaet' is er alleen in het Latijn (vertaald door Willebrord Snellius): De staticae praxi.
   
   In 1603 legde Christoph Grienberger uit hoe zelfs een gouden Aarde verplaatst zou kunnen worden (met figuur); zie ook de in noot 5 genoemde Gaspar Schott, Magia universalis (1658) III & IV, 235: "Machina II. Ons glossocomum [>], door de macht waarvan de hele aarde verplaatst wordt, als ze van goud was", zie Icon. X en Icon. XI.
     Een recent idee om de aarde te verplaatsen is: een komeet bijsturen met een raketmotor. Die moet dan een zodanige baan om de zon beschrijven dat hij energie van Jupiter aan de aarde kan geven. Zo kunnen we in enkele miljarden jaren de baan van Mars bereiken (Zenith juli/aug. 2001, Korycansky, 2001).   «

   
   

5. De grenzen van wat mogelijk was met werktuigen zijn ook door anderen verkend, zoals bijvoorbeeld te zien is in het schetsboek van Villard de Honnecourt (zie de vijzel-animatie), en bij de 'database machine drawings' van het Archimedes Project: afbeeldingen uit werken van Agricola, Besson, Caus, Errard, Mariano (Taccola) e. a. (de laatstgenoemde tekende ca. 1430 ook een bootwagen; hij was een voortreffelijk tekenaar, zie ook bij IMSS en: 'De machinis', 'De ingeneis', Siena, omstreeks 1427-1441).
     Anonymus der Hussitenkriege, 'Liber machinarum', 1430 [BSB Clm 197, I, met 197, II: Taccola].
   BNF ms Latin 7239: Taccola, 'De re militari et machinis bellicis', ca. 1453.
   
   Errard liet in Le premier livre des instruments mathematiques mechaniques (1584, p. 11) zien hoe een boot over een dam getild kon worden met behulp van een kraan. En Salomon de Caus beschreef in Von gewaltsamen Bewegungen (1615, p. 7v-8r) een 'Almachtich' dat de kracht bijna 3 miljoen maal vergroot, met zesmaal een overbrengingsverhouding van 1 op 12.
     Salomon de Caus, Les raisons des forces mouvantes 1615, p. 8r.
     Zie ook de figuren van Octavius de Strada (1617, 1618), Vittorio Zonca Novo teatro di machine et edificii (1607, 1621) Agostino Ramelli, Le diverse et artificiose machine..., (1588); en Claude Flamand, Les mathematicques ... (1597), p. 221 (in boek 6, h. 6: 'De la multiplication des forces mouvantes ...').
   
   Het hiernaast afgebeelde werktuig heeft driemaal een overbrengingsverhouding van 1 op 12, en daarmee kan de hand aan de kruk een gewicht van 86400 pond ophijsen, als zonder het instrument 50 pond getild kan worden; aldus Marin Mersenne, Cogitata physico-mathematica (1644), 'Tractatus mechanicus', p. 40.
   Meer raderen gebruiken heeft geen zin, zegt Mersenne, want er is geen materiaal dat sterk genoeg is. Hij bespreekt ook de lengte van de kruk, en de dikte van de onderste as bij N.

   Afbeelding: IMSS.

   
   John Wilkins, Mathematicall Magick. Or, the wonders that may be performed by mechanicall geometry (1648), toont op p. 98 ook een afbeelding van zo'n 'Almachtich', met wel twaalf raderparen.
   
   In Stevins rekenvoorbeeld zijn er vier raderparen, met een totale overbrengingsverhouding van 1 op 162 (driemaal 1 op 3, eenmaal 1 op 6). De afmetingen van kruk en laatste as geven dan een resulterende verhouding van 1 op 216. De kruk kan ook op een andere as geplaatst worden, zodat er niet te lang gezwengeld behoeft te worden als de vereiste kracht niet heel groot is (het niet benodigde gedeelte is dan te ontkoppelen). Het ontwerp van Stevin lijkt dus minder onrealistisch dan andere genoemde voorstellen.
   
   Nog in 1658 wordt door Gaspar Schott het "Pancratium infinitae potentiae Simonis Stevini" genoemd en uitgelegd, in Magia universalis naturae et artis, Pars III & IV, p. 249 en Icon. XII, Fig. III.

   In hetzelfde jaar laat Paolo Casati het 'Pancratium' of 'Glossocomum'*) van Archimedes bespreken door Galileï, Guldin en Mersenne, in: Terra machinis mota (1658), p. 3-13.
   

   
   Pancratium of glossocomum volgens Casati
   Afbeelding: ECHO
   Op p. 9 staat een praktische opmerking: de tanden van een tandrad gaan te snel kapot, reparatie is gemakkelijker bij gebruik van touwen (zie andere fig.).
   
     *)  Glossocomum - kist, oorspronkelijk: foedraal voor mondstukken als van fluit, later: geldbuidel, geldkist. Dit woord werd eveneens gebruikt door Mersenne (1644, zie voorgaande afbeelding), en is ook te vinden bij het hydraulisch orgel van Hero, in Commandino, Heronis Alexandrini Spiritalium liber (1575), p. 70 (figuur, links): kistje voor mondstuk van orgelpijp — Engl.: "small boxes, like those used for money".
   Baldi: "una sorte di cassettino ...", in De gli automati (1589), p. 44.
   Een 'glossocomum' werd ook een chirurgisch instrument bij het zetten van gebroken benen (Beinlade), ook met andere spelling 'glossocomium', zie ook de figuur bij Ambroise Paré, 1585.
   
   Schott kende Casati, en diens verklaring van de krachtvergroting wordt aangehaald in bovengenoemd werk, Magiae universalis naturae et artis, Pars III & IV, Würzburg 1658, p. 223.
     Een interessante opmerking op p. 230:

   Met dit kunstmiddel hebben, zoals Aristoteles ook vermeldt, de Ouden de standbeelden van hun goden toegerust, met binnenin verborgen wielen, zodat — terwijl door heimelijk draaien aan het ene de andere zouden gaan bewegen, en daardoor verschillende bewegingen van de standbeelden zouden ontstaan — het onwetende volk ertoe gebracht zou worden het aan een wonder toe te schrijven, omdat het niet wist dat het op natuurlijke wijze gebeurde.

   De index in Magia geeft aan dat de term 'Glossocomum' voorkomt op:
   - p. 231 (figuur ernaast, naar Pappus - zie hieronder),
   - p. 235 (gouden aarde bewegen - vgl. Grienberger hierboven),
   - p. 245 (andere vorm).
   Verder vinden we daar:
   - p. 234: Bettini, Apiaria (zie fig.),
   - p. 243: berekening, zoals bij Stevin, hoe lang een omwenteling van het grootste rad duurt,
   - p. 248: de bovengenoemde Besson, het woord 'Charistion', en Mersenne (zie Universae geometriae ..., 1644, 471, met een nuchtere opmerking: het duurt veel te lang).
     Meer over Schott in: Michael John Gorman, 'Athanasius Kircher and the baroque culture of machines' (waarin ook de "frauds of the ancient priests" aan de orde komen).

   
   

   
   Glossocomum
   in: Pappi Alexandri mathematicae collectiones,
   ed. Commandino, 1588 (p. 314v) en 1660, p. 461.
   
   Een later werk met figuren van machines: Georg Andreas Boeckler, Theatrum machinarum novum, 1661 (Duits), 1662 (Latijn).
   
   Francesco Lana de Terzi, Magisterium naturae et artis (1684) geeft ook figuren, alle aan het eind. Op blad II vinden we er twee die zijn overgenomen van Stevin: Fig. 22, 'Almachtich' (p. 35) en Fig. 23, 'schepen over dammen' (p. 37). Uitleg ervan geeft Lana op p. 87-88: "Pancratium seu Glossocomum ...", Hero en Pappus worden genoemd, en "Stevinus lib. 3 staticae prop. 10".
   Figurenblad XIII, F. 5: de 'clootcrans' van Stevin, behandeld op p. 321 bij beweging op een hellend vlak.