W E E G C O N S T is die, welcke leert de Redenen, Eueredenheden, ende ghedaenten vande ghewichten ofte swaerheden der lichamen.
 H E L I I C K de Meetconst {Geometria} ansiet der formen grootheden niet hare swaerheden, houdende die alleenelick voor euen ofte oneuen, diens grootheden euen ofte oneuen sijn; Alsoo ansiet ter contrarie de Weegconst haer swaerheden, niet haer grootheden, houdende die voor euen ende oneuen, diens ghewichten euen ofte oneuen sijn:
H E L I I C K de Meetconst {Geometria} ansiet der formen grootheden niet hare swaerheden, houdende die alleenelick voor euen ofte oneuen, diens grootheden euen ofte oneuen sijn; Alsoo ansiet ter contrarie de Weegconst haer swaerheden, niet haer grootheden, houdende die voor euen ende oneuen, diens ghewichten euen ofte oneuen sijn:
Ende ghelijck diens voornamelicke wercking bestaet int ondersoucken der Redenen Eueredenheden, ende Ghedaenten {* Rationum, proportionum & qualitatum.} haerder grootheden, Also desens int ondersoucken der Redenen Eueredenheden, ende ghedaenten haerder swaerheden ofte ghewichten, welcker bescriuing t'voornemen is deses handels.
Swaerheydt eens lichaems, is de macht sijnder daling in ghestelde plaets.
D E swaerheydt ofte lichticheydt die wy ghemeenelick segghen een lichaem te hebben, en is niet sijn eyghen wesentlicke ghedaente, maer veroirsaect uyt sijn ghemeenschap met een ander (wiens breeder verclaring wy elders gheschict hebben) want veel Stoffen {Materia.} die swaer sijn inde locht, worden licht beuonden int water, ende de lichte inde locht, sijn elders swaer;
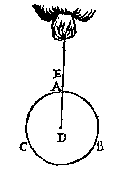
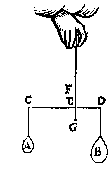
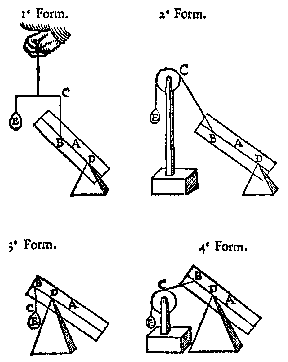
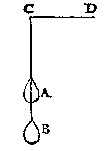 E N D E de swaerheydt hoogher ofte leegher hangende, altijt van een selfde gewicht te blijven.
E N D E de swaerheydt hoogher ofte leegher hangende, altijt van een selfde gewicht te blijven. 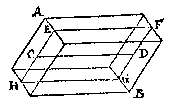
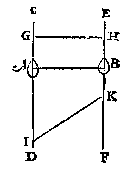
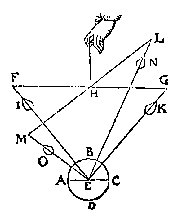 alwaer het blijct, dat de hanghende linien FI, ende GK, gheen euewydighe en sijn, maer onder naerder malcander dan bouen;
alwaer het blijct, dat de hanghende linien FI, ende GK, gheen euewydighe en sijn, maer onder naerder malcander dan bouen; 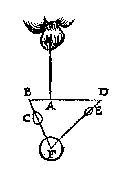 Maer om t'selue by voorbeelt te verclaren, laet AB den cortsten erm sijn, diens ghewicht C, ende AD den langsten erm, diens ghewicht E in sulcken reden sy tot tghewicht C, als AB tot AD, ende F sy t'sweerelts middelpunt; Alwaer blijct dat den houck FBA plomper ende den rechthouck naerder is, dan den houck ADF, waer uyt volght (door tvoornoemde 22e voorstel) dat C naer de ghestalt swaerder sal sijn dan E.
Maer om t'selue by voorbeelt te verclaren, laet AB den cortsten erm sijn, diens ghewicht C, ende AD den langsten erm, diens ghewicht E in sulcken reden sy tot tghewicht C, als AB tot AD, ende F sy t'sweerelts middelpunt; Alwaer blijct dat den houck FBA plomper ende den rechthouck naerder is, dan den houck ADF, waer uyt volght (door tvoornoemde 22e voorstel) dat C naer de ghestalt swaerder sal sijn dan E.