Overzicht , Inleiding , hefboom , limiet , hellend vlak , kracht , ingenieur , Noten
Stevins Weeghconst
Het eerste deel bestaat uit twee boeken, samen 95 blz, hier verdeeld in 10 stukken.
De Beghinselen des Waterwichts Anhang Byvough
Zie deel 1 van Principal Works voor een facsimile.
InleidingDe Beghinselen der Weeghconst begint met definities, en dan komen de stellingen, compleet met: T' G H E G H E V E N , T' B E G H E E R D E , T' B E W Y S , zoals Euclides dit gedaan had voor de meetkunde. De weegkunde is wat we nu noemen de Statica, een onderdeel van de Mechanica. Voor wie snel een indruk wil krijgen: Meester Simon legt de hefboomwet uit. Hefboomwet
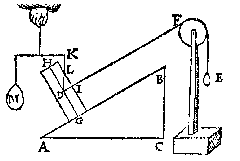
In de 13e eeuw vertaalde Willem van Moerbeke enkele werken van Archimedes in het Latijn. Maar pas in de 16e eeuw (omstreeks Stevins geboortedatum 1) ging men in Europa grondig bestuderen wat Archimedes had nagelaten. Italiaanse wiskundigen, o.a. de in de Weeghconst genoemde Commandino, gebruikten zijn geschriften bij het bepalen van zwaartepunten. Simon Stevin zette Archimedes' werk voort op een originele manier. Hij gaf bijvoorbeeld bij de zwaartepunten een eenvoudiger bewijs, met de limiet-methode: als het verschil tussen een driehoek en zijn ingeschreven vierhoeken willekeurig klein gemaakt kan worden door meer lijnen te trekken, dan is er geen verschil. Dit "oneindelick naerderen" komt in de plaats van het oude 'bewijs uit het ongerijmde' (reductio ad absurdum) en is te zien als voorloper van de differentiaalrekening van Newton en Leibniz. De methode is ook te vinden in het 'Waterwicht', bij de berekening van het "gheprang" van water tegen een wand. Een reguliere universitaire opleiding had Stevin niet genoten, en hij had dus niet geleerd dat Aristoteles de enige bron van alle kennis was 2. Maar hij las diens werk wel, en hij vond uitspraken waarmee hij het niet eens was. Bijvoorbeeld: dat bij de valbeweging het zwaarste voorwerp het eerst beneden zou zijn. Stevin kwam tot de conclusie dat de navolgers van Aristoteles geen "kennis der oirsaken" hadden 3. Bij het vernuftige bewijs van de hefboomwet in de Weeghconst is Archimedes zijn voorbeeld, maar hij maakt het meer aanschouwelijk. Vijf tekeningen geven duidelijk het verloop van het betoog aan: hij neemt een "pilaer" (balk), opgehangen in het zwaartepunt, en snijdt deze dan in twee ongelijke stukken. Zo laat hij op een simpele manier zien dat algemeen geldt: "ghelijck de swaerste swaerheyt tot de lichtste, also den langsten erm tot den cortsten". Geen draaibeweging is nodig, en in de Anhang wordt nog eens benadrukt: "Dat der evestaltwichtighen oirsaeck niet en schuylt onder de ronden beschreven met d'uytersten der ermen." [>] Hellend vlak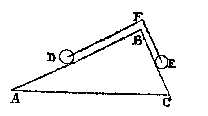 Twee even zware bollen, verbonden door een touw (via een katrol), steunen op twee vlakken met verschillende hellingshoek. Is er evenwicht?
Wie deze situatie voor het eerst ziet denkt misschien van wel. Ghelijck des driehoucx rechter sijde tot de slincker, also t'staltwicht des cloots op de slincker sijde, tottet staltwicht des cloots op de rechter sijde.Het 'staltwicht' is het gewichtseffect in een opstelling, hier dus op het hellend vlak. Dus: als AB = 2 BC dan trekt E dubbel zo hard als D. Hoe bewijs je deze stelling? Stevin toont het aan zonder wiskundige uiteenzetting, in het beroemde 'clootcrans-bewijs' met de bollenkrans (zijn 'logo'). Hij gebruikt wel veel woorden, een verkorte versie staat in Parels.
Na zijn gouden greep met de krans volgt meer nieuws. Daarvoor heeft hij nodig het 'hefwicht', al gebruikt in voorstel 14. Waar wij eenvoudig een krachtmeter (geijkte veer) zouden gebruiken, daar laat hij een gewicht omhoog trekken via een gelijkarmige balans. In voorstel 13 bewees hij eerst: daelwicht en hefwicht doen aan gelijke armen gelijke 'ghewelden'. En in bepaling 12 liet hij al zien dat het ook scheef kan: met een katrol.
ghelijck LD tot DI , also M tot E.De 'pilaer' wordt in die stand gehouden hetzij door gewicht E en de helling (DI en IL als krachtvectoren), hetzij door de balans met M (vector DL als tegengestelde van de zwaartekracht). Nu kan ook berekend worden welk "treckwicht" (zoals E) nodig is bij een wagen op een helling. En dan komt een belangrijk inzicht te voorschijn: bij een wagen op een horizontaal vlak, en bij een schip in het water, is de benodigde trekkracht nul! Zij "behouven gheen vlieghesterctens macht tot haer verroersel" meer dan de "verhindernissen". Deze uitspraak is nog maar een haarbreedte verwijderd van het traagheidsprincipe. 4 Hierna onderzoekt Stevin allerlei andere situaties waarin de pilaer door twee krachten in een bepaalde stand gehouden wordt. Steeds geldt: Ghelijck rechtheflini tot scheefheflini, also rechthefwicht tot scheefhefwicht.(Deze zin neemt hij in zijn lofrede op de taal als voorbeeld: in welke andere taal kun je dit zo zeggen, zonder "langhe redenen te stellen, die t'onderscheyt der palen [4 termen], ende de form der everedenheyt overal seer verduysteren"?) Tenslotte laat hij zien "Alle de everedenheden, welcke hier vooren beschreven sijn vanden pilaer [...] te wesen van yder lichaem", met in de tekening een boomstam in scheve stand. KrachtSwaerheydt eens lichaems, is de macht sijnder daling in ghestelde plaets.In de Weeghdaet heeft hij het uitgebreid over zijn krachtwerktuig het "Almachtich [...] van oneindelicke cracht". Het woord 'cracht' komt daar nog een aantal malen voor, maar meestal is het macht: een gheduerighe macht soo groot als 25 lb souden neertrecken, t'welck ick de macht schat van een man, ende grooter als hy wilIn het boek Waterwicht staat bij de berekening van de kracht van water tegen een wand (bodem): swaerheyts middelpunt [..] vande macht des gheprangs vergaert inden bodemDe woordenlijst bij de 'Uytspraeck' over de taal geeft: Kracht. Force. Virtus.Later, in de Byvough, is het meestal 'ghewelt', zoals in Tauwicht, waermen by verstaen mach, een handel verclarende wat ghewelt datter ancomt op yder tau, van verscheyden tauwen daer een bekende swaerheyt anhangt.En in "dese ghemeene weeghconstighe reghel": Ghelijck wech des doenders, tot wech des lijders, Meer over de natuurkunde van Stevin in: Parels, en: inleiding bij Weeghdaet en bij Waterwicht. Zie Devreese over de betekenis van het werk van Simon Stevin voor de natuurkunde. Stevin de ingenieurop dat sy lijckformigher soude siin an t'ghene inde daet gheschiet (want men can binnen int lichaem qualick de linien [...] trecken) wy hebben de hanghende lini [..] int voorbeelt uytwendich ghenomen.Het oog voor de praktijk wordt genoemd in het eind van het Anhang-hoofdstuk bij de wet van Archimedes: daetlicke weghinghen (naer welcke de Spiegheling {Theoria.} altijt opsicht behoort te nemen)In tegenstelling tot zijn grote voorbeeld Archimedes vindt Stevin dat de theorie in dienst moet staan van de toepassing. In zijn opdracht van de Weeghdaet vergelijkt hij zijn Beghinselen der Weeghconst met een "stercke grondt" waarop een "ghebau" gezet gaat worden. De "spieghelingh" moet leiden tot de "daet of tuychwerckelicken handel". Na de Beghinselen des Waterwichts komt ook de Waterwichtdaet, maar daarvan is er alleen een 'Anvang'. Zie ook: Spiegeling en daad. Het is niet vreemd te stellen dat Stevins bekendheid met de praktijk ook leidde tot een betere theorie. Bijvoorbeeld: bij het meten van krachten had hij een 'scheefwaeg' met een katrol, om duer ogenschijnelicke eruaring te sien, ondersoucken, ende verstaen, de waerheydt der voorstellen vande everedenheydt soodanigher ghewichten int eerste bouck Wisconstlick {Mathematicè.} beschreven, op datmen hem alsoo te vastelicker betrau in t'ghene men inde Daet tot s'menschen voordering daer duer uytrechten wil.Maar "op datmen een scheefwaegh heb die scherpelick weghe" moet er wel een goede katrol zijn: Ick heb voor my daer toe doen drayen een caterol van bosboom, wiens dickte niet meer en was dan als den rugghe van een dun mes, ende des rondts middellini van ontrent vijf duymen, ende den as (al met den anderen ghedraeyt) van yvoor, vande dickte als een cleermakers naelde, te weten soo dun alst den draeybanck lijden mocht.Stevin was ook ontwerper: zijn watermolen werd enkele jaren na het verschijnen van de 'Weeghconst' met succes gebruikt in Delft. Maar een dergelijke molen in IJsselstein functioneerde niet goed. Dat zal hem veel geleerd hebben over uitvoeringsproblemen, evenals een kennelijke ontgoocheling na zijn belofte van "stercker werck" met het Almachtige werktuig.
Voor de watermolen en enkele andere uitvindingen is octrooi verleend: namaak verboden. Bij het braadspit (dat ook uurwerk en wieger was) werd expliciet vermeld dat daar op "int ijzer" moest staan Stevins beeldmerk, de clootcrans. In 1600 werd in Leiden een ingenieursschool opgericht voor landmeters en vestingbouwers. Simon Stevin stelde het programma op voor deze "Duytsche Mathematique".
Noten |