SIMON STEVIN BRUGGHELINCK"Spiegheling en Daet"Jozef T. DevreeseUniversiteit Antwerpen &Technische Universiteit Eindhoven"Magic Without Magic" luidt de titel van een huldeboek (1) - vol met nieuwste ontwikkelingen in de fysica - aangeboden bij de zestigste verjaardag van Professor John Archibald Wheeler, de befaamde hedendaagse natuurkundige, specialist in de kernfysica, astrofysicus, één der pioniers van de recente opbloei van de algemene relativiteitstheorie, en die tevens een grote school creëerde.  Figuur 1. Ruim vierhonderd jaar geleden verscheen - "Tot Leyden, Inde Druckerye van Christoffel Plantijn" (1586) - het meesterlijke werk van historische betekenis: "De Beghinselen der Weeghconst beschreven duer Simon Stevin van Brugghe". In het vignet op de geïllustreerde voorpagina is, op de banier, de uitspraak "Wonder en is gheen Wonder" aangebracht. Intuïtief wordt "Wonder en is gheen Wonder" mooi als "Magic without Magic" vertaald. Juistere en meer inspirerende vertaling van Simon Stevins adagium kan moeilijk worden bedacht en het opduiken van deze gedachte in de moderne toonaangevende natuurkunde-literatuur zoals op de titelpagina van Wheelers huldeboek, ook als deze onafhankelijk zou zijn "herontdekt", is als een hulde aan Simon Stevin op te vatten. Kan men stellen dat Simon Stevins bijdragen tot de mechanica en de hydrostatica alleszins met te weinig bronvermelding aan bod komen in de moderne basis-leerboeken dan stemt het tot voldoening dat in het meesterwerk van de hedendaagse basis-natuurkunde leerboeken, namelijk in de onvolprezen "Feynman lectures on Physics" Simon Stevins bewijs met de "Clootcrans" betreffende de samenstellingswet voor krachten, de hemel wordt ingeprezen. Eerst ontwikkelt Feynman twee andere afleidingen van deze samenstellingswet doch dan stelt hij: "Cleverness, however, is relative. It can be deduced in a way which is even more brilliant, discovered by Stevinus and inscribed on his tombstone." (2)  Figuur 2. The epitaph of Stevinus Uit: "The Feynman Lectures on Physics." Hierbij merkt Feynman op: "Cleverness, however, is relative. It can be deduced in a way which is even more brilliant, discovered by Stevinus and inscribed on his tombstone, (If you get an epitaph like that on your gravestone, you are doing fine.)" Het is de geïnspireerde meester van de 20-eeuwse theoretische natuurkunde, "de Mozart der Fysica", Richard Feynman, niet ontgaan dat Simon Stevin een uiterst geniaal - in eerste instantie intuïtief - idee naar voor bracht toen hij de samenstellingswet voor krachten afleidde. Wel dient opgemerkt dat het graf van Simon Stevin niet werd teruggevonden, zodat Feynmans opmerking over de inscriptie op de grafzerk, evenals de uitlating iets verder in de hoger geciteerde leerboektekst: "If you get an epitaph like that on your gravestone, you are doing fine" als dichterlijke vrijheid zijn op te vatten. Moderne beoefenaars van de klassieke mechanica die in contact komen met Stevins bewijs met de "crans" (of "kogelsnoer") zijn veelal opgetogen. Bijvoorbeeld Martin Gutzwiller, een leidende autoriteit op dit gebied - dat thans een nieuwe opleving kent - vertelde op een conferentie in Tutzing met groot enthousiasme en oprechte bewondering over dit wonderbaarlijke gedachtenexperiment van Simon Stevin (3). De bovenstaande voorbeelden illustreren hoe de betekenis van het werk van Simon Stevin bij een aantal hedendaagse fysici gestadig meer doordringt, al mag hier worden aan toegevoegd dat de geniale Joseph Louis Lagrange en geleerden als Ernst Mach zich bewust waren van de waarde van Simon Stevins werk in de mechanica. Lagrange noemt het bewijs met het kogelsnoer "une démonstration très ingénieuse" (4). De doelstelling van dit essay is na te gaan in welk opzicht het werk van Simon Stevin grensverleggend en innoverend is geweest. De discussie wordt daarbij geconcentreerd op de natuurkunde alhoewel ook summier iets wordt gezegd over andere gebieden van wetenschap en technologie, die in meer detail aan bod komen in de overige bijdragen tot dit volume. De hoofdconclusie zal zijn dat Simon Stevin een aantal inderdaad grensverleggende bijdragen heeft geleverd in het bijzonder tot de natuurkunde en dit zowel op het methodologische als op het conceptuele vlak. Daarbij kan tevens gesteld worden dat de onvolprezen biograaf van Simon Stevin, E.J. Dijksterhuis, in zijn quasi-definitief standaardwerk (5) de bijdrage van Simon Stevin zeer precies en genuanceerd analyseert en belicht, doch dat hij daarbij de betekenis ervan, voornamelijk voor de natuurkunde, misschien toch nog eerder onderschat. I. Summiere biografische gegevens over Simon Stevin. II. De innovaties van Simon Stevin op het gebied der natuurkunde en de betekenis ervan. III. (Appendix) Korte nota over Simon Stevin en de Nederlandse Taal. I. De schaarse biografische gegevens over SIMON STEVIN.Wat de biografische gegevens betreft kan men Simon Stevin enigszins vergelijken met Pieter Bruegel de Oude: ook deze sublieme schilder en humanist kennen we vrijwel uitsluitend door zijn werk, al is de kans groot dat althans enige zelfportretten in zijn werk kunnen worden geïdentificeerd. Van het, naar verluidt door een tijdgenoot geschilderde portret van Simon Stevin dat zich in de bibliotheek van de Universiteit te Leiden bevindt, kunnen we enkel hopen dat het ons inderdaad een idee geeft van zijn uiterlijke verschijning. De schaarse gegevens over de levensloop van Simon Stevin werden door E.J. Dijksterhuis kritisch geëvalueerd en beperken zich essentieel tot wat in Tabel I wordt weergegeven. TABEL I. LEVENSLOOP VAN SIMON STEVIN Geboren te Brugge in 1548 als de natuurlijke zoon van Antheunis Stevin (geboren in Veurne) en Cathelyne vander Poort. Klerk bij de Imposten (Belastingen) bij het Brugse Vrije (1577-1581). Tevoren: kassier en boekhouder in Antwerpen (periode niet precies bekend). Vestigt zich te Leiden in 1581, schrijft zich in als student aan de universiteit aldaar op 16 februari 1583. Rond 1590 wordt hij raadsman van Prins Maurits, graaf van Nassau. Op 68-jarige leeftijd treedt hij in het huwelijk met Catherine Cray, toen zij reeds vier kinderen hadden. Simon Stevin overlijdt in 1620, wellicht in Den Haag.  Deze tabel leert ons niet of Simon Stevin een inspirerende leermeester had, noch wat het aanknopingspunt was dat het hem mogelijk maakte de eerste belangrijke vooruitgang op het gebied van de statica en hydrostatica te maken die iets toevoegt aan het werk van Archimedes. Was hij een autodidact? Waarom verliet hij Brugge om eerst in Antwerpen en later te leiden te verblijven? Hoe kan verklaard worden dat hij, als het ware uit het niets, in 1585 "De Thiende" en in 1586 een meesterwerk als "De Beghinselen der Weeghconst" kan voortbrengen?  Figuur 3. Wanneer heeft hij de buitenlandse reizen gemaakt die hem toelieten gedetailleerde waterbouwkundige ontwerpen te maken ondermeer voor de stad Danzig? Op deze vragen moeten we het antwoord schuldig blijven. We kunnen slechts hopen dat, in nog niet ontgonnen archieven, nieuwe gegevens over Simon Stevin aan het licht zullen komen, wie weet samen met het belangrijke manuscript "vant Lochtwicht" dat jammer genoeg is verloren gegaan. II. Innovaties op het gebied van de natuurkunde.Essentieel kan gesteld worden dat nog niets was toegevoegd aan het werk van Archimedes op het gebied van de mechanica en de hydrostatica, met uitzondering van de behandeling in de school rond Johannes Nemorarius (? - 1237) van de samenstelling van krachten op grond van de dynamische theorie toegeschreven aan Aristoteles. Ter situering: Simon Stevin overleed 22 jaar vóór Newton werd geboren, hij was 16 jaar ouder dan Galileo Galilei (1564-1642) en leefde ook decades vroeger dan Pascal (1623-1662) of Christiaan Huyghens (1629-1695). Simon Stevin was een tijdgenoot van figuren als Calvijn, Palestrina, El Greco. Het is belangrijk het werk van Simon Stevin te situeren tegen de achtergrond van de kennis en de stand van wetenschap en techniek in de 16de eeuw. Het is bijvoorbeeld pas rond 1550 dat werken van Appolonius, Archimedes, Pappus e.a. stilaan algemeen beschikbaar worden in Latijnse vertalingen. Tegen deze historische achtergrond treedt Simon Stevin naar voren met briljante bijdragen op het gebied van de statica resp. de hydrostatica: In de statica bewijst hij (met de "crans") de wet der samenstelling van krachten. In de hydrostatica ontdekt hij de vermaarde hydrostatische paradox en brengt hij tevens een meer algemeen bewijs van de wet van Archimedes naar voren dan door de grote man van Syracuse was gegeven. Wat daarbij opvalt is dat hij telkens uiterst originele gedachtenexperimenten introduceert. Merkwaardig is ook dat hij hetzelfde principe, namelijk de onmogelijkheid van het perpetuum mobile, - in het prachtige Nederlands van Simon Stevin "eeuwigh roersel...dat valsch is..." - (figuur 4) weet te gebruiken, voor het eerst in de geschiedenis, zowel bij de behandeling in de statica "met het kogelsnoer" als bij de afleiding van de wet van Archimedes uit de hydrostatica.  Figuur 4. Zijn bewijsvoering in de statica komt strikt genomen neer op een toepassing van de wet van het behoud van energie die pas rond 1840, i.e. 260 jaar later, door verschillende geleerden, waaronder von Helmholtz (1821-1894) werd geformuleerd. Zoals Dijksterhuis terecht opmerkt plaatst Simon Stevin zich aldus op één lijn met Torricelli en Huyghens die eveneens de wet van het behoud van energie anticipeerden. In zijn bewijs "met het kogelsnoer" van de samenstellingswet voor krachten gebruikt Simon Stevin opnieuw op intuïtieve wijze de facto reeds het symmetrie-concept dat zo centraal staat in de theoretische natuurkunde van deze tijd. Laten we enige der innoverende bijdragen van Simon Stevin tot de statica en de hydrstatica in meer detail bekijken. II.1. "WONDER EN IS GHEEN WONDER" Figuur 5. Simon Stevin beschouwt een rechthoekige driehoek ABC waar AB tweemaal zo lang is als BC en "den grondt AC evewijdich vanden sichteinder,..". Hij veronderstelt dat een bol D ligt op de zijde AB en een bol E, met hetzelfde gewicht "evewichtig ende evegroot", op BC. In zijn gedachtenexperiment beeldt hij zich nu in dat deze twee bollen deel uitmaken van een aantal (identieke) bollen. Deze bollen maken samen een snoer uit dat kan glijden over de vaste punten S, T en V. "Laet ons maecken rondom den driehouck ABC eenen crans van veerthien clooten, evegroot, evewichtig, ende evewijt van malcanderen ... al ghesnoert an een lini...". Dit snoer is de "clootcrans". Het aantal bollen op AB is dus tweemaal het aantal op BC. Simon Stevin wil nu bewijzen dat het zogenaamde "staltwicht" van de bollen D, R, Q, P op AB gelijk is aan dat van de bollen E, F op BC. Met "staltwicht" bedoelt Simon Stevin het "effectief" gewicht van een bol langs een hellend vlak; dit is de componente van de kracht langs een hellend vlak. Veronderstel dat het eerste "staltwicht" (dat van de bollen P, Q, R, D) groter is dan het tweede (dat van de bollen E, F). De vier denkbeeldige bollen O, N, M, L zijn in evenwicht met de vier denkbeeldige bollen G, H, I, K; bijgevolg zal de groep van acht bollen D...L zwaarder wegen dan de groep van zes bollen E....K. Daarom zullen deze acht bollen naar beneden rollen en de andere zes naar boven: "de acht cloten sullen neerwaert rollen, ende d'ander zes rijsen...". Daarbij gaat nu iedere bol op een bepaald ogenblik de plaats innnemen van zijn voorganger. Beschouwd als een geheel zal de positie van de "crans" evenwel niet gewijzigd worden door deze substitutie. "Den crans der clooten sal alsulcken ghestalt hebben als sy te vooren dede, ....". De beweging zal daarom voortduren; m.a.w. de bollen zullen een perpetuum mobile uitvoeren wat absurd is: "ende de clooten sullen uyt haer selven een eeuwich roersel maken, t' welck valsch is." De crans zal daarom in rust blijven, de linkse en de rechtse groep bollen "balanceren" elkaar. Indien links de vier bollen O...L worden weggedacht en rechts de vier bollen G...K, die de andere vier in evenwicht houden, zal het evenwicht niet verstoord worden. Daarom volgt de stelling: omdat de vier bollen D, R, Q, P de twee E, F in evenwicht houden, is het "staltwicht" van E tweemaal dat van D net zoals de lengte van AB tweemaal die van BC is. De keuze van de verhouding der lengten AB en BC is evenwel willekeurig. Er volgt dan de beroemde samenstellingswet dat twee bollen op hellende vlakken, verbonden door een touw dat over een katrol loopt bij de top T in evenwicht zullen zijn, indien de reden van hun gewicht gelijk is aan de reden van de lengte van de twee. De opmerking die strikt genomen kan geformuleerd worden, is dat in afwezigheid van wrijving, luchtweerstand enz. een perpetuum mobile wel mogelijk is en dat de klassieke mechanica precies onder deze idealiserende voorwaarde wordt geformuleerd. Het is evenwel perfect mogelijk om de redenering van Stevin lichtjes aan te passen en in het kader van de klassieke mechanica - maar dan op grond van de wet van het behoud van energie - aan te tonen dat de "crans" zoals opgevat door Simon Stevin niet in beweging zal treden indien er geen beginsnelheid wordt gegeven. Simon Stevin ontleedt verder in de "Beghinselen der Weeghconst", uitgaande van zijn bovengeschetst bewijs, talrijke situaties waarbij gewichten op hellende vlakken optreden.  Figuur 6. Hij analyseert het evenwicht van lichamen met een vast punt, (figuur 7) het evenwicht als drie krachten optreden, hij bepaalt zwaartepunten van vlakken ("vande Platten") en van ruimtelijke figuren ("Nu vande vinding der swaerheits middelpunten vande lichamen").  Figuur 7. Bij deze zwaartepuntsbepalingen volgt hij essentieel de methode van Archimedes doch maakt daarbij een historische vooruitgang tot de formulering van het begrip limiet. (ref. 5 p 129). In de "Weeghdaet" worden dan tal van practische toepassingen behandeld, betreffende werktuigen waarbij wrijvingskrachten, weer-standen, valproeven... aan bod komen. Een merkwaardige verhandeling te vinden in het "Vierde deel des byvoughs der weeghconst" is "Vande Toomprang", tot stand gekomen op vraag van Prins Maurits "Hebbende sijn Vorstelicke Ghenade van kintsche daghen af tot noch toe, hem gheduerlick met grooten yver seer vlietich gheoeffent inde Ruyterconst, ....". Hierin behandelt Simon Stevin hoe de druk van het bit op de lip en van de kinketting op de onderkaak van het paard afhangen. Het zal ook de hedendaagse ruiter nog interesseren.  Figuur 8. Op één plaats, bij studies over de wrijvingskrachten, komt Simon Stevin in contact met de dynamica: hij bestudeert er de valbeweging (met als bedoeling zekere inzichten van Aristoteles terzake te weerleggen). Dit heeft geleid tot de uitvoering van een valproef waarbij Stevin, met de hulp van zijn vriend Johan Cornets de Groot, twee loden bollen met verschillend gewicht gelijktijdig liet vallen vanop een hoogte van dertig voet, en concludeerde (alhoewel niet helemaal correct) dat beide bollen op hetzelfde ogenblik op een plank vallen. Deze valproef werd uitgevoerd vóór 1586 waarbij dient opgemerkt (ref. 6 p. 130) dat de gelijkaardige valproef vanop de scheve toren van Pisa, die aan Galileo wordt toegeschreven - als die al werd uitgevoerd - pas na 1589 kan worden gesitueerd. Toch moet worden gezegd dat Simon Stevin - afgezien van zijn opmerkingen over de dynamica van Aristoteles - geen verdere bijdragen heeft geleverd tot de dynamica, in tegenstelling tot Galileo. De valproef van Simon Stevin illustreert wel de waarde die hij hecht aan het experiment bij de opbouw der natuurwetenschap. De overgang naar de "hoe"-vraag in de natuurkunde, die aan de naam Galileo wordt geassocieerd, wordt dus in die zin door Simon Stevin geanticipeerd: waarschijnlijk was dit methodologisch concept bij verschillende geleerden onafhankelijk aanwezig in die periode. Stevin was daarbij een één der eersten maar de naam van Galileo Galilei groeide uit tot een symbolisch begrip om de overgang van middeleeuws naar modern denken te karakteriseren: hoe complex deze overgang was en hoe controversieel de bijdragen der verschillende actors leert men bijvoorbeeld uit een werk zoals "New Perspectives on Galileo" dat in 1978 werd gepubliceerd. We kunnen stellen dat Simon Stevin in de mechanica essentieel bijdragen leverde tot de statica; daarbij nam hij de draad op waar Archimedes gebleven was. Hij verrijkte de statica met prachtige bewijsvoeringen en concepten. Het belang van zijn bijdrage ligt vooral in het vinden van nieuwe wegen en methodes om de mechanica uit te bouwen. Verder in dit essay wordt teruggekeerd op de betekenis van de bijdrage van Stevin tot de statica. In zijn boek "The Scientific Revolution" gaat H.F. Cohen (7) dieper in op de vraag waarom Stevin en zijn tijdgenoten er voor het eerst in slaagden nieuwe paden te vinden en een nieuwe start te nemen na de lange stilstand sinds de Grieken en Archimedes. II.2. BIJDRAGEN TOT DE HYDROSTATICAZoals hoger vermeld zijn de bijdragen van Simon Stevin tot de hydrostatica van grensverleggende betekenis. Zijn methodes zijn opnieuw innoverend en conceptueel verdienen ze het epitheton "magisch", een aantal resultaten zijn nieuw met de "hydrostatische paradox" als hoogtepunt. Stevin berekende de kracht van water per eenheid van oppervlak zodat hij feitelijk als eerste met het begrip druk werkte, weliswaar zonder het begrip te voeren tot de universele dimensie eraan gegeven door Pascal. Op het gebied der hydrostatica was Simon Stevin de eerste die iets toevoegde aan het werk van Archimedes. Hij was trouwens een der eersten die het werk van Archimedes las in latijnse vertaling. Het was pas rond 1550 dat de uit het Grieks naar het Latijn vertaalde werken van Archimedes beschikbaar werden. Er zij nog opgemerkt dat het een Vlaming was, Willem van Moerbeke, een vriend van Thomas van Aquino, die - in het Vaticaan - werken van Archimedes had vertaald rond 1250. Willem, die een grondige en uitzonderlijke kennis bezat van de Oosterse talen, bracht het tenandere tot patriarch van Constantinopel. In dit essay zal herinnerd worden aan de bewijsvoering van Simon Stevin ter veralgemenining van de wet van Archimedes. tevens zal het gedachtenexperiment uitgelegd worden waarmede Simon Stevin de kracht berekent die een vloeistof, door haar gewicht, uitoefent op de bodem van een vat. II.2.a. Veralgemeende afleiding van de wet van ArchimedesII.2.b. De hydrostatische paradox van Simon Stevin."..dat 1 lb. waters meer ghewelts sal connen doen, dan hondert duysent ponden...".Hier wordt niet ingegaan op de details van de bewijs-voering: er wordt verkozen een sleutel-element ervan te belichten: Bij de bepaling van de kracht door water uitgeoefend op de bodem "des waters" wordt opnieuw een pareltje van een gedachten-experiment aangebracht: Stevin gaat uit van de vaten in bijgaande figuur 9. 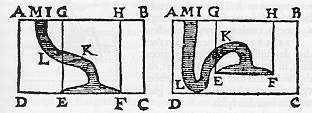
 Figuur 9. Om de kracht op het grondvlak aangegeven met EF te bepalen, beeldt hij zich in dat het water overal in vaten is bevroren (i.e. vervangen door een "stijflichaem"), behalve in de gearceerde gebieden. De kracht op EF zal daardoor geen wijziging ondergaan. Hieruit volgt dat deze kracht steeds gelijk is aan het gewicht van de kolom EFGH. De hydrostatische paradox, dat de kracht op de bodem niet hoeft gelijk te zijn aan het gewicht van de inhoud ..volgt hieruit. Het zou aangewezen zijn in de literatuur naar de "hydro-statische paradox van Simon Stevin" te verwijzen. De hydrostatische paradox leidt tot de hydrostatische krik of vijzel zoals Simon Stevin expliciet inziet. Het toegepaste stuk van de studie van het waterwicht beslaat slechts acht pagina's en werd door Stevin "Anvang der Waterwicht-daet" genoemd. Zich richtende "Anden Leser" verklaart hij: "...welcke ons niet weerdich dunckende, den naem van Waterwichtdaet te verstrecken,....., wij noemen Anvang van dien." en: "de rest t'sijnder tijdt te verwachten." Voor zover bekend is, heeft Stevin geen vollediger Waterwichtdaet laten verschijnen. De drie voorstellen (proposities) in de Anvang der Waterwichtdaet betreffen de vraag hoe diep een schip zinkt in het water, (figuur 10) verder voorbeelden ter illustratie van de hydrostatische paradox en tenslotte "D'Oir-saeck te verclaren waerom een mensch diep onder t'water swemmende, niet doot gheprangt en wort, van t'groot ghewicht des waters op hem ligghende". Speciale aandacht verdient hier Stevins experiment om aan te tonen hoe opwaartse druk optreedt in een vloeistof. Dit experiment wordt vandaag nog getoond in vele secundaire scholen (figuur 11).  Figuur 10.  Figuur 11. Met de bovenstaande onderwerpen werden de belangrijkste bijdragen van Simon Stevin tot de natuurkunde aangegeven. Andere bijdragen van Stevin die verband houden met de natuurkunde zijn te vinden in geschriften over "De Hemelloop", "Van de Spiegheling der Ebbenvloet", "De Havenvindingh", "De Zeijlstreken" en in "Spiegheling der Singconst". Van belang is alleszins de kinematische getijdentheorie die Stevin ontwierp en die het werk van Newton voorbereidt. Ook merkwaardig is dat Simon Stevin de eerste blijkt te zijn (ref. 5) die een volledige theorie geeft voor het toonsysteem waarbij het octaaf in twaalf gelijke halve tonen wordt ingedeeld. daarbij corrigeert hij het werk van de vader van Galileo, die wiskundige en musicus was. Op deze bijdrage buiten de statica en de hydrostatica wordt in dit essay niet verder ingegaan. II.3. De betekenis van het werk van Simon Stevin over NatuurkundeHet feit dat Simon Stevin het kernbegrip hydrostatische druk niet in zijn algemeenheid invoerde (dit is de bijdrage van Pascal die er toe kwam na heel wat gissen en missen) komt niet in mindering van zijn unieke ontdekking van de belangrijke natuurwet die de hydrostatische paradox is. Trouwens aangezien Simon Stevin, zoals hoger vermeld, de grootte van de kracht uitgeoefend door een vloeistof op een willekeurig oppervlak berekende werkte hij reeds - telkens waar nodig - met het concept druk. Het grote inzicht van Pascal bestond erin het algemeen karakter van het begrip druk en de uniforme voortplanting van de druk in een vloeistof voorop te stellen. Het is verwonderlijk dat in de vakliteratuur niet stelselmatig wordt verwezen naar de "(hydrostatische) paradox van Stevin" - wat terecht zou zijn - maar naar de "hydrostatische paradox" tout court. Men spreekt wel over "het principe van Huyghens" (in de optica), of over de "wet van Pascal" (hydrostatica) waar het om vindingen van dezelfde allure gaat. De associatie van zijn naam aan een wet of formule is niet enkel een gepast eerbetoon aan de ontdekker, het verstrekt de onderzoeker spelenderwijs een zeker inzicht in de geschiedkundige evolutie van zijn discipline, ook al kan een toewijzing wel eens controversieel zijn. Getransformeerd naar de 20ste eeuw is de ontdekking van de "hydrostatische paradox van Simon Stevin" slechts te vergelijken met de doorbraken van de eerste orde zoals bijvoorbeeld de "val der pariteit" bedacht door Lee en Yang. Het gaat hierbij om het vinden van natuurwetten. Talrijke geleerden hebben belangwekkende bijdragen geleverd tot de wetenschap zonder daarom een natuurwet te ontdekken. Bij Stevins bewijs met de "clootcrans" is de methode van de afleiding - het originele gedachtenexperiment - minstens zo belangrijk als het bekomen resultaat dat reeds via een andere weg bekend was. Het gedachtenexperiment met de clootcrans is m.i. zelfs zo prachtig en verrassend, dat het pas door Einstein in estetische waarde en doeltreffendheid werd benaderd. (n.a.v. de ondertussen overbekende gedachtenexperimenten uit de speciale relativiteitstheorie met bewegende treinen, liften, klokken.) Het is inderdaad een visionnaire stap van Simon Stevin, een meesterlijk inzicht, om - bij het bepalen van het evenwicht der bollen aan de hand van figuur 3 - in gedachten de crans te sluiten door zich een snoer identische bollen in de vorm van een halve cirkel in te beelden, daarbij intuïtief gebruik makend van een diepe symmetrie en deze concepten dan nog te combineren met de onmogelijkheid van het perpetuum mobile om tenslotte, doeltreffend, de samenstellingswet voor krachten te voorschijn te toveren. Het weze herhaald dat, wat het perpetuum mobile betreft, Simon Stevin de eerste is in de geschiedenis der wetenschap die er gebruik van maakt. Zoals hoger gezegd toont een nadere analyse weliswaar dat bij de afleiding met het kogelsnoer eigenlijk gebruik dient te worden gemaakt van het principe van het behoud van energie en dat strikt genomen hier niet het verwerpen van het perpetuum mobile de kern is. Zoals Dijksterhuis terecht opmerkt doet dit niets af van de de fundamenteel juiste intuïtie van Simon Stevin. Het is van belang erop te wijzen dat in de natuurwetenschap het methodologische, vooral met de diepgang die hier bij Simon Stevin wordt bereikt, van uitnemende betekenis is. Zo we het intuïtieve clootcrans bewijs rigoreus formuleren dan zijn de sleutel-ingrediënten: - Het "transponeren" van het probleem door de toevoeging van denkbeeldige bollen die dus niet echt optreden in het probleem. In Simon Stevins gedachtenexperiment is dit een verre van voor de hand liggende transformatie van het probleem; het betreft hier iets diepers dan het bedenken van een hulpconstructie bij een oefening van vlakke meetkunde: Stevins "sluiten" van het snoer doet eerder denken aan gesofistikeerde methodes uit de hedendaagse theoretische natuurkunde waar bij bepaalde fundamentele problemen - en dit wordt dan technisch - fictieve deeltjes ("ghosts") werden toegevoegd aan de theorie, teneinde toe te laten dat zekere onfysische benaderingen in de loop der berekening kunnen worden vermeden. Aan het eind der berekening verdwijnen de "ghosts" net als de denkbeeldige bollen van Simon Stevins crans. - Het toepassen van een symmetrieprincipe waarbij het evenwicht van de vier bollen O N M L met de vier bollen G H I K wordt geponeerd. Strikt genomen is het slechts de intuïtie ten gronde aan deze symmetriebeschouwing die overleeft. In de theoretische natuurkunde van de twintigste eeuw is de grote kracht van symmetrieprincipes gebleken: o.a. het bestaan van sommige elementaire deeltjes - die nadien experimenteel werden ontdekt - werd via symmetrieprincipes voorspeld. Het gebruik van een - zij het intuïtief - symmetrieargument door Simon Stevin is dus opnieuw zijn tijd ver vooruit. - Behoud van energie: zoals hoger aangegeven komt het principe van het behoud van energie tussen bij een rigoreuse formulering van het kogelsnoerbewijs en - in strikte zin - niet het verwerpen van het perpetuum mobile. Simon Stevin beweegt zich hier in het limietgeval van infinitesimale wrijving, en behoort - samen met Huyghens en Torricelli - en drie eeuwen voor de verdere studie van deze begrippen tot de eersten die deze behoudsprincipes reeds aanvoelden. De methodes en gedachtenexperimenten die Simon Stevin invoert zijn niet van het type die onmiddellijk door tijdgenoten, volgelingen en volgende generaties (kunnen) worden overgenomen (zoals wel het geval was met de infinitesimaalrekening die door de Bernouilli's en Euler tot een universeel instrumentarium werd ontwikkeld). Het gaat bij Stevin over dermate diepgaande intuïtie dat de methodes waarnaar wordt verwezen pas in de 19-de resp. de 20-ste eeuw een hoge vlucht blijken te gaan nemen. Ook het combineren van niet minder dan drie originele principes verdient de aandacht evenals het feit dat een bewijs resulteert dat, zoals Dijksterhuis terecht onderstreept, geen voorkennis veronderstelt bij de lezer (dit is waarschijnlijk uniek in de natuurkunde). Het bewijs met de clootcrans is niet enkel onovertroffen om het gestelde doel te bereiken (het krachtenparallellogram) doch het mag in het geheel der natuurkunde gelden als een pareltje van estetica, klaarheid, overtuigingskracht. II.4. De natuurwetenschappelijke methodeReferenties.
NaschriftIII. Appendix. Simon Stevin en de nederlandse Taal.In een recente studie (8) heeft M. Kool, voor de rekenkunde, grondiger onderzocht welke termen uit de werken van Simon Stevin al dan niet reeds vroeger kunnen worden aangetroffen. Als woorden die Simon Stevin heeft geput uit wat reeds in de taal voorhanden was noemt de auteur van (8) ondermeer: menichvuldighen, noemer, rekenen, somme, telder, tellen, vergaderen (voor: optellen) viercant, wortel, worteltrecken, mael, verkeerdelijk, aftrekken, cijfer, deelder, deler, delinghe, ghebroken (= breuk), getal, helft. Neologismen die Simon Stevin met grote waarschijnlijkheid heeft ingevoerd en die de Auteur van (8) alleszins niet in vroegere werken heeft aangetroffen, zijn uytbreng (product bij een vermenigvuldiging), parich (even), onparich (oneven), soomenichmael (betekent: quotiënt), teerlincxwortel (derde machtswortel), thiendetal (getal uitgedrukt volgens het decimaal systeem), ghebreeckende (het getal nul). Het zou interessant zijn indien ook voor de natuurkunde, de zeevaartkunde, de krijgswetenschap enz. een grondiger studie zou worden gemaakt van de originele bijdragen van Simon Stevin tot de Nederlandse taal. In 1995 verscheen een studie (9) waarin o.a. werd nagegaan in hoeverre termen die in de werken van Simon Stevin voor het eerst werden gebruikt, overgenomen zijn in het eerste systematisch en grondig woordenboek van het Nederlands dat door Kiliaen, corrector in de Officina Plantiniana, in 1599 werd uitgegeven (10). De motieven van Simon Stevin ten gunste van het gebruik van het Duytsch worden ondermeer uiteengezet in de inleiding tot de Weeghconst onder de hoofding: "Uytspraeck van de weerdicheyt der Duytsche tael". Op de analyse van deze gronden en van de sociale en culturele achtergrond waartegen Simon Stevin voor de volkstaal opkomt wordt hier niet verder ingegaan. |