20, 21: Evenredigheid , 22, 23: trekwicht , 24: grootste geweld bij rechte hoek ,
25 - 27: hangende pilaer , 28: ieder lichaam
|
W E S E N D E inden as des pilaers een vastpunt, ende een roerlick, daer an hy door een rechthefwicht ende scheefhefwicht in seker standt ghehouden wort: Ghelijck rechtheflini tot scheefheflini, also rechthefwicht tot scheefhefwicht. |
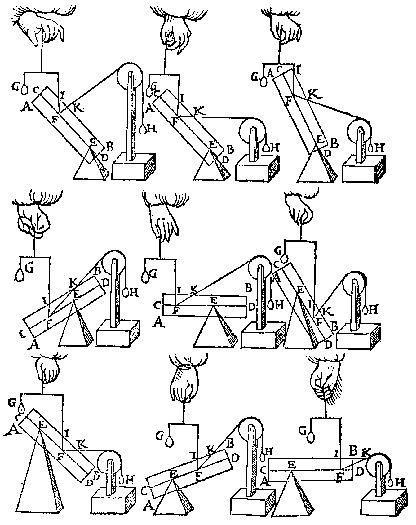
| T' G H E G H E V E N. Laet AB een pilaer sijn diens as CD, ende t'vastpunt E, ende roerlick punt F, daeran den pilaer door t'rechthefwicht G in die ghestalt ghehouden wort, daer an oock den pilaer door t'scheefhefwicht H (welverstaende G gheweert sijnde) in die ghestalt ghehouden wort, ende de rechtheflini snie de sijde des pilaers in I, maer de scheefheflini snie de selue sijde in K: Ick seg dat ghelijck de rechtheflini IF, tot de scheefheflini FK, alsoo trechthefwicht G, tot het scheefhefwicht H, waer af t'bewys uyt de voorgaende openbaer is. |

[ 52 ]
|
T' B E S L V Y T. Wesende dan inden as des pilaers een vastpunt, &c. M E R C K T. Soo eenighe der linien als IF, FK, de sijde des pilaers niet en sneen, men sal die sijde voorder trecken tot dat sy ghesneen wort, als inde voorgaende laetste form.
W E S E N D E inden as des pilaers een vastpunt, ende een roerlick, daer an hy door een rechtdaelwicht ende scheefdaelwicht in seker standt gehouden wort: Ghelijck rechtdaellini tot scheefdaellini, also rechtdaelwicht tot scheefdaelwicht.
*) Feil: inde form EL is te lanck want sy moet euen siin met EF. |
|
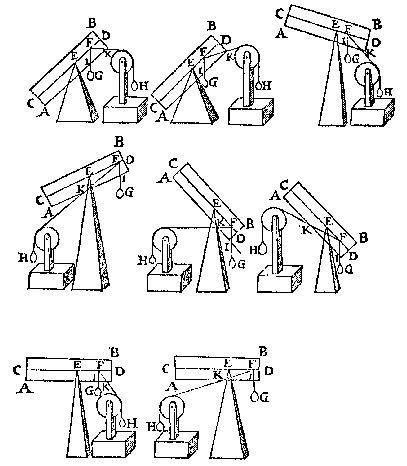
T' G H E G H E V E N. Laet ABCD een pilaer sijn weghende 6 lb, ende ghedeelt als int Ie voorstel, ende t'vastpunt sy X, ende het roerende punt S, an t'welck gheuoecht sy een onbekent scheefhefwicht Y, met den pilaer euestaltwichtich, ende sijn scheefheflini snie de sijde des pilaers AB in Œ. T' B E G H E E R D E. Wy moeten dat onbekende scheefhefwicht Y bekent maken. T' W E R C K. Men sal sien wat rechthefwicht an S den pilaer in die ghestalt soude houden, 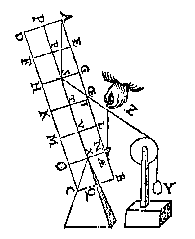 wort beuonden door 14e voorstel, van 4 lb, daer naer salmen ondersoucken wat reden eenighe hanghende lini {Perpendicularis.} als ZÆ, heeft tot ZŒ, ick neme als van 2 tot 1, daer uyt seg ick 2 gheeft 1, wat t'rechthefwicht van 4 lb ? comt voor Y 2 lb, t'welck ick seg sijn waer ghewicht te sijne.
wort beuonden door 14e voorstel, van 4 lb, daer naer salmen ondersoucken wat reden eenighe hanghende lini {Perpendicularis.} als ZÆ, heeft tot ZŒ, ick neme als van 2 tot 1, daer uyt seg ick 2 gheeft 1, wat t'rechthefwicht van 4 lb ? comt voor Y 2 lb, t'welck ick seg sijn waer ghewicht te sijne.T' B E R E Y T S E L. Laet ons trecken de hanghende door S welcke sy AS. T' B E W Y S. Ghelijck AS tot SŒ, also t'rechthefwicht tottet scheefhefwicht Y door het 20e voorstel, maer den driehouck ŒZB, is ghelijck anden driehouck ŒSA, welcker lijckstandighe linien {Homologa.} sijn ŒZ met ŒS, ende ZÆ met SA: Daerom ghelijck AS tot SŒ, alsoo ÆZ tot ZŒ, ende vervolghens ghelijck ÆZ 2, tot ZŒ I, also t'rechthefwicht 4 lb tot Y, daerom Y weghende 2 lb is bekent ghemaect, t'welck wy bewysen moesten. Ende sghelijcx sal den voortganck sijn in allen anderen voorbeelden. T' B E S L V Y T. Wesende dan ghegheuen een bekenden pilaer met een vastpunt inden as, &c. W Y souden inde wercking hebben mueghen segghen, AS 2, gheeft SŒ 1, wat t'rechthefwicht 4 lb ? comt voor Y 2 lb, maer op dat sy lijckformigher soude siin an t'ghene inde daet gheschiet (want men can binnen int lichaem qualick de linien AS, SŒ trecken) wy hebben de hanghende lini ZÆ int voorbeelt uytwendich ghenomen. T I S openbaer door de verkeerde ende oueranderde Eueredenheydt {Inuersam & alternam proportionem.}, hoe dat elck van d'ander onbekende palen {Terminorum} als Rechthefwycht, Rechtheflini, Scheefheflini, Pilaer, door drie bekende palen altijdt bekent sullen worden, welcker bescriuing wy om de cortheyt achterlaten. |
|
E V E N ghewichten der trecklinien van een selfde punt des as, ende op verscheyden sijden met den as euen houcken makende; doen anden pilaer euen ghewelden. T G H E. Laet AB een pilaer sijn diens as CD, ende vastpunt daer in E, en t'roerlick punt F, an t'welck een scheefhefwicht G sy, dat den pilaer in die ghestalt houde, ende diens scheefheflini FH. Laet oock an t'selue punt F gheuoucht wesen een scheefhefwicht I, ouer d'ander sijde, ende met G euewichtich, ende diens scheefheflini FK, den houck KFD euen make anden houck HFC. 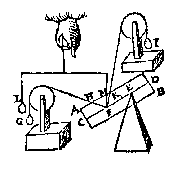 T' B E G H E E R D E. Wy moeten bewysen dat I anden pilaer euen sulcken ghewelt doet als G, te weten dat I (G gheweert sijnde) den pilaer oock in die ghestalt sal houden.
T' B E G H E E R D E. Wy moeten bewysen dat I anden pilaer euen sulcken ghewelt doet als G, te weten dat I (G gheweert sijnde) den pilaer oock in die ghestalt sal houden.T' B E R E Y T S E L. Laet an t'punt F gheuoucht worden t'rechthefwicht L dat den pilaer oock in die ghestalt can houden, ende sijn rechtheflini sy FM. T' B E W Y S. Want de linien FH, FK, sijn tusschen de euewydighe {Parallelas.} HK, CD, ende dat den houck HFC, euen is (door t'ghegheuen) an den houck KFD, so sijn FH ende FK euen. waer uyt volght dat ghelijck MF tot FH, alsoo MF tot FK, Maer ghelijck MF tot FH, alsoo L tot G, daerom oock ghelijck MF tot FK, also L tot G; maer I is euen an G door t'ghestelde, ghelijck dan MF tot FK, alsoo L tot I. T'welck so sijnde, I houdt den pilaer in die ghestalt door het 20 voorstel. Sghelijcx sal oock t'bewijs sijn in alle anderen voorbeelden. T' B E S L V Y T. Euen ghewichten dan der trecklinien van een selfde punt des as, ende op verscheyden sijden met den as euen houcken makende; doen anden pilaer euen ghewelden, t'welck wy bewysen moesten. A L S des ghewichts trecklini rechthouckich op den as is; Soo doedet anden pilaer ghegeuener ghestalt de grootste ghewelt. |
|
T' G H E G H E V E N. Laet AB een pilaer sijn diens as CD, ende vastpunt E, ende roerlick punt F, waer an gheuoucht is t'scheefhefwicht G, dat den pilaer in die ghestalt houdt, ende also dat sijn scheefheflini HF rechthouckich op den as CD is; Laet oock an F gheuoucht worden t'scheefhefwicht I, euen an G, ende sijn scheefheflini sy KF. T' B E G H E E R D E. Wy moeten bewysen dat G meerder ghewelt doet anden pilaer, dan I, oock gheen meerder ghewelt daer an doen en can. T' B E R E Y T S E L. Laet ons an F voughen t'rechthefwicht L dat den pilaer in die ghestalt houden can, diens rechtheflini FM. T' B E W Y S.
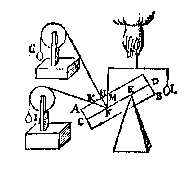 D E S bewysredens {Syllogismi.} tweede voorstel wort aldus bethoont, T'ghewicht G (t'welck den pilaer in die ghestalt houdt) heeft sulcken reden tot L, als HF tot FM, maer I is euen an G, ende KF is meerder dan FH {47.v.I.b. E.}, daerom I heeft minder reden tot L, dan KF tot FM, waer duer soo wy bouen gheseyt hebben, t'ghewicht I is te licht om den pilaer in die ghestalt te houden; maer G cander hem in houden, G dan doet anden pilaer meerder ghewelt dan I.
D E S bewysredens {Syllogismi.} tweede voorstel wort aldus bethoont, T'ghewicht G (t'welck den pilaer in die ghestalt houdt) heeft sulcken reden tot L, als HF tot FM, maer I is euen an G, ende KF is meerder dan FH {47.v.I.b. E.}, daerom I heeft minder reden tot L, dan KF tot FM, waer duer soo wy bouen gheseyt hebben, t'ghewicht I is te licht om den pilaer in die ghestalt te houden; maer G cander hem in houden, G dan doet anden pilaer meerder ghewelt dan I.Maer dat G daer an gheen meerder doen en can, is daer uyt openbaer, dat van F op de sijde des pilaers gheen corter lini en can ghetrocken worden dan FH, anghesien sy daer op rechthouckich is. T' B E S L V Y T. Als dan des ghewichts trecklini rechthouckich op den as is, soo doedet an den pilaer ghegheuener ghestalt de grootste ghewelt, t'welck wy bewysen moesten. H E T blijft [blijct] dat hoe de houcken der trecklinien vande ghewichten, op den as den rechthouck naerder sijn, hoe de ghewichten meerder ghewelt doen; Ende ter contrarie hoe sy vanden rechthouck meer verschillen, hoe de ghewichten minder ghewelt doen. |
|
T W E E oneuewydighe linien daer een pilaer an hangt beyde oneindelick voortghetrocken, snien malcanderen inde swaerheydts middellini des pilaers. T' G H E G H E V E N. Laet AB een pilaer sijn hanghende ande twee oneuewydighe linien CD, EF, welcke voortghetrocken sijn tot G, H, sniende malcanderen in I. 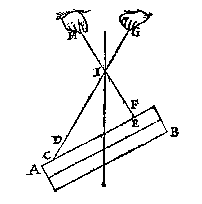 T' B E G H E E R D E. Wy moeten bewysen dattet punt I inde swaerheyts middellini is des pilaers AB.
T' B E G H E E R D E. Wy moeten bewysen dattet punt I inde swaerheyts middellini is des pilaers AB.T B E W Y S. Den houck FEC, ofte IEC, ofte HEC, is al een selfden houck, also oock is DCE, ofte ICE, ofte GCE, daerom wat punten wy inde linien HE, ende CG voor uytersten nemen, den pilaer houdt daer an sijn ghegheuen standt. Laet ons nemen I, ghemeen uyterste punt van d'een ende d'ander lini, den pilaer dan houdt daer an sijn ghegeuen standt. Maer hanghende den pilaer an t'punt I, so is de hanghende {Perpendicularis.} door I des pilaers swaerheydts middellini inde welcke I is. T' G H E G H E V E N. Laet AB een pilaer sijn hanghende ande oneuewydighe linien CD, EF, welcke voortghetrocken sijn tot G, H, sniende malcanderen in I. T' B E G H E E R D E. Wy moeten bewysen dattet punt I, inde swaerheyts middellini is des pilaers AB. T B E W Y S. Laet ons DG ende FH ansien voor stylen ofte stiue linien daer den pilaer op rust, welcke door de 2e begheerte niet en breken noch en buyghen; |
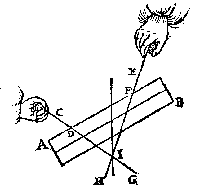 der seluer ghewelt is euen ande ghewelt der linien CD, EF, want ghelijck dese den pilaer in sijn ghegheuen standt houden alsoo oock die. Ende wat punten wy inde linien DG, FH voor uytersten nemen, den pilaer houdt daer op sijn ghegheuen standt.
der seluer ghewelt is euen ande ghewelt der linien CD, EF, want ghelijck dese den pilaer in sijn ghegheuen standt houden alsoo oock die. Ende wat punten wy inde linien DG, FH voor uytersten nemen, den pilaer houdt daer op sijn ghegheuen standt. Laet ons nemen I, ghemeen uyterste punt van d'een en d'ander lini; den pilaer dan houdt daer op (Wisconstlick {Mathematicè.} verstaende) sijn ghegheuen standt, maer rustende den pilaer op t'punt I, soo is de hanghende door I des pilaers swaerheydts middellini, inde welcke I is. T' G H E G H E V E N. Laet AB een pilaer sijn welcke in die standt ghehouden wort door de scheefdaellini CD, ende scheefheflini EF, de selue sijn voortghetrocken tot G, H, sniende malcanderen in I. 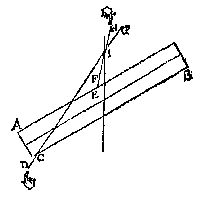 T' B E G H E E R D E. Wy moeten bewysen dat I inde swaerheydts middellini is des pilaers AB.
T' B E G H E E R D E. Wy moeten bewysen dat I inde swaerheydts middellini is des pilaers AB.T' B E W Y S. Laet ons GC ansien voor styl, ofte stijue lini ende nemen dat de macht die an D int neertrecken was, nu neerstekende sy in yder punt tusschen C en G daermen haer stelt, ende den pilaer AB, sal alsoo op allen punten diemen tusschen C, G ende E, H voor uytersten neemt, sijn ghegheuen standt houden. Laet ons nemen I ghemeen uyterste van d'een en d'ander lini, den pilaer dan houdt daer an sijn ghegheuen standt; maer hanghende den pilaer an t'punt I, de hanghende door I is des pilaers swaerheyts middellini, inde welcke I is. T' G H E G H E V E N. Laet AB een pilaer sijn, welcke in die standt ghehouden wort door de scheefdaellini CD, ende de scheefheflini EF, de selue sijn voortghetrocken tot G H, sniende malcanderen in I. T' B E G H E E R D E. Wy moeten bewysen dat I inde swaerheyts middellini is des pilaers AB. |
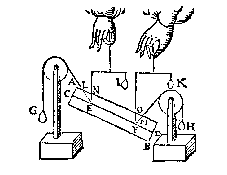 T' B E W Y S. Laet ons F ansien voor vastpunt, ende E voor t'roerlick, daerom (door het 20e voorstel) ghelijck LE tot EN, alsoo G tot I. Laet ons ten tweeden E ansien voor vastpunt, ende F voor t'roerlick; Daerom (door t'voornoemde 20e voorstel) ghelijck MF tot FO, alsoo H tot K.
T' B E W Y S. Laet ons F ansien voor vastpunt, ende E voor t'roerlick, daerom (door het 20e voorstel) ghelijck LE tot EN, alsoo G tot I. Laet ons ten tweeden E ansien voor vastpunt, ende F voor t'roerlick; Daerom (door t'voornoemde 20e voorstel) ghelijck MF tot FO, alsoo H tot K.T' B E S L V Y T. Hanghende dan een pilaer euestaltwichtich teghen twee scheefhefwichten: Ghelijc scheefheflini tot rechtheflini, alsoo elck scheefhefwicht tot sijn rechthefwicht, t'welck wy bewysen moesten. 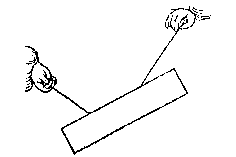
H A N G H E N D E een bekende pilaer an twee oneuewydighe linien als hier neuen; Tblyckt dat bekent sal worden hoe veel ghewichts an yder lini hangt, ofte hoe veel ghewelts yder lini doet. 
W Y hebben tot veel voorbeelden der voorstellen deses boucx, ghenomen den pilaer, als bequaemste form tot de verclaring des voornemens oock vastpunt ende roerlickpunt ghestelt inden as. Wy sullen nu door dit laetste voorstel, bethoonen de reghelen van dien ghemeen te wesen ouer alle formen der lichamen hodanich sy siin met vastpunt ende roerlickpunt daert valt. |
|
A L L E de eueredenheden {Proportiones.}, welcke hier vooren beschreuen sijn vanden pilaer tot de ghewichten an hem hanghende, ende dier ghewichten linien: De selue te wesen van yder lichaem tot de ghewichten an hem alsoo hanghende, ende dier ghewichten linien. 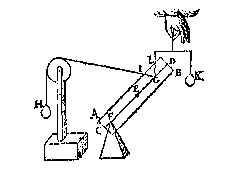 T' G H E G H E V E N. Laet ons t'voorbeelt nemen der eueredenheydt des 20e voorstels aldus: Het sy een pilaer AB, diens as CD, ende swaerheyts middelpunt E, ende vastpunt daer in F, ende roerlick punt G, an t'welc gheuoucht sy een scheefhefwicht H, dat den pilaer in die ghestalt houde, diens scheefheflini GI. Daer naer trechthefwicht K, dat den pilaer oock in die ghestalt houde, diens rechtheflini GL, alwaer wy segghen, ghelijck IG tot GL, also H tot K.
T' G H E G H E V E N. Laet ons t'voorbeelt nemen der eueredenheydt des 20e voorstels aldus: Het sy een pilaer AB, diens as CD, ende swaerheyts middelpunt E, ende vastpunt daer in F, ende roerlick punt G, an t'welc gheuoucht sy een scheefhefwicht H, dat den pilaer in die ghestalt houde, diens scheefheflini GI. Daer naer trechthefwicht K, dat den pilaer oock in die ghestalt houde, diens rechtheflini GL, alwaer wy segghen, ghelijck IG tot GL, also H tot K.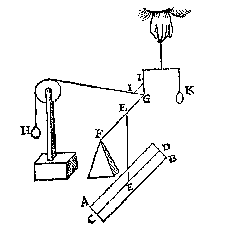 T' B E G H E E R D E. Wy moeten bewysen dat dese eueredenheydt niet alleenlick also en bestaet in t'lichaem AB een pilaer sijnde, maer van sulcke form alst valt.
T' B E G H E E R D E. Wy moeten bewysen dat dese eueredenheydt niet alleenlick also en bestaet in t'lichaem AB een pilaer sijnde, maer van sulcke form alst valt.T B E W Y S. Laet ons den pilaer AB (blijuende de linien FG ende IL op haer plaetsen) neertrecken, alsoo dat hy bliue hanghende an sijn swaerheyts middelpunt {Centrum grauitatis.} E, wiens ghestalt dan sy als hier neuens. Ende door de 3e begheerte den pilaer en veroirsaect op de punten F, G, gheen ander swaerheydt dan d'eerste; ende alles blijft noch euestaltwichtich, ende ghelijck IG tot GL, alsoo noch H tot K. |
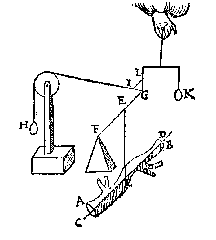 L A E T nu de form des pilaers (al de stoff bliuende) verandert worden in eenighe ander ongheschickte form, als AB hier neuens, diens swaerheydts middelpunt E sy, ende een rechte lini daer duer CD (welcke vinding des swaerheyts middelpunts ende rechter linien inde Weeghdaet verclaert sal worden, werckelick, niet Wisconstelick {Mechanicè non Mathematicè.}) ende alles blijft noch euestaltwichtich, ende ghelijck IG tot GL, also noch H tot K.
L A E T nu de form des pilaers (al de stoff bliuende) verandert worden in eenighe ander ongheschickte form, als AB hier neuens, diens swaerheydts middelpunt E sy, ende een rechte lini daer duer CD (welcke vinding des swaerheyts middelpunts ende rechter linien inde Weeghdaet verclaert sal worden, werckelick, niet Wisconstelick {Mechanicè non Mathematicè.}) ende alles blijft noch euestaltwichtich, ende ghelijck IG tot GL, also noch H tot K.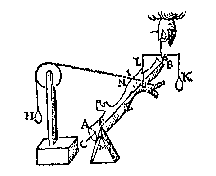 L A E T nu t'lichaem AB opghetrocken worden, tot dat FG is inde lini CD, wiens ghestalt dan sy als hier neuens, ende alles blijft noch euestaltwichtich: want het lichaem AB hoogher ofte leegher hanghende, blijft van een selfde ghewicht door de 3e begheerte, ende veruolghens ghelijck IG tot GL, alsoo noch H tot K. De eueredenheydt dan des 20e voorstels en is niet alleenelick alsoo met den pilaer, maer met yder lichaem: Ende der ghelijcke salmen oock alsoo bethoonen van al t'ghene hier vooren in alle d'ander voorstellen vanden pilaer gheseyt is.
L A E T nu t'lichaem AB opghetrocken worden, tot dat FG is inde lini CD, wiens ghestalt dan sy als hier neuens, ende alles blijft noch euestaltwichtich: want het lichaem AB hoogher ofte leegher hanghende, blijft van een selfde ghewicht door de 3e begheerte, ende veruolghens ghelijck IG tot GL, alsoo noch H tot K. De eueredenheydt dan des 20e voorstels en is niet alleenelick alsoo met den pilaer, maer met yder lichaem: Ende der ghelijcke salmen oock alsoo bethoonen van al t'ghene hier vooren in alle d'ander voorstellen vanden pilaer gheseyt is.T' B E S L V Y T. Alle de eueredenheden dan, welcke hier vooren bescreuen sijn vanden pilaer tot de ghewichten an hem hanghende, ende dier ghewichten linien; de selue sijn van yder lichaem tot de ghewichten an hem alsoo hanghende, ende dier ghewichten linien, t'welck wy bewysen moesten. |
|
T I S oock openbaer dat de ghegheuen punten als F, G, niet nootsaeckelick en moeten inde lini CD sijn, maer daert valt. by voorbeelt ande uytersten des lichaems M, N, Want voortghetrocken de lini IN tot inde rechte CD, t'welck ick neem te vallen in G, sghelijcx ghetrocken door M de hanghende {Perpendiculars.} tot inde lini CD, welcke ick neem te vallen in F, de voornoemde eueredenheydt, te weten ghelijck IG tot GL, alsoo H tot K, blijft noch staende.
|