VIe V O O R B E E L T.
T' G H E G H E V E N. Laet ABCDEF een ongheschickt seshouck sijn.
T' B E G H E E R D E. Wy moeten sijn swaerheydts middelpunt vinden.
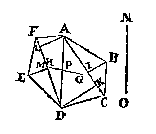 T' W E R C K. Men sal den seshouck deelen in vier driehoucken, met eenighe linien als AC, AD, FD, vindende daer naer het swaerheyts middelpunt des vierhoucx ADCB door het 4e voorbeelt, t'welck G sy, ende des vierhoucx ADEF, t'welck H sy, ende de lini HG is balck. Daernaer ghetrocken BI ende DK rechthouckich op AC, insghelijcx AL ende EM beyde rechthouckich op FD, men sal der drie linien welcker eerste FD, de tweede AC, de derde BI met KD, vinden de vierde euerednighe, welcke NO sy, deelende den balck HG in P, also dat den erm PG, sulcken reden hebbe tot den erm PH, ghelijck AL met EM, tot NO; Ick seg dat P het begheerde swaerheyts middelpunt is.
T' W E R C K. Men sal den seshouck deelen in vier driehoucken, met eenighe linien als AC, AD, FD, vindende daer naer het swaerheyts middelpunt des vierhoucx ADCB door het 4e voorbeelt, t'welck G sy, ende des vierhoucx ADEF, t'welck H sy, ende de lini HG is balck. Daernaer ghetrocken BI ende DK rechthouckich op AC, insghelijcx AL ende EM beyde rechthouckich op FD, men sal der drie linien welcker eerste FD, de tweede AC, de derde BI met KD, vinden de vierde euerednighe, welcke NO sy, deelende den balck HG in P, also dat den erm PG, sulcken reden hebbe tot den erm PH, ghelijck AL met EM, tot NO; Ick seg dat P het begheerde swaerheyts middelpunt is.
Ende soo salmen voort mueghen varen met ander veelhouckeghe platten.
[ Figuren ingevoegd.]
|
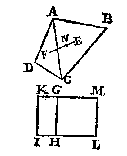
T' B E W Y S. Ghelijck int eerste voorbeelt HI tot HL, alsoo den erm NE tot den erm NF, maer {I. v. 6. B. E.} ghelijck HI tot HL, alsoo den vierhouck GHIK, tot den vierhouck GHLM, ghelijck dan GHIK tot GHLM, also NE tot NF, maer GHIK is euen an den driehouck ACD, ende GHLM anden driehouck ACB door t'werck, ghelijck dan den driehouck ACD tot ACB, alsoo den erm NE tot NF.
Het punt dan N is (door het Ie voorstel des Ien boucx) des vierhoucx swaerheyts middelpunt. Sghelijcx sal oock bewijs sijn des 2e ende 3en voorbeelts.
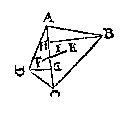
T'vierde voorbeelt is openbaer als wy bewesen hebben dat ghelijck DG, tot HB, alsoo den driehouck ACD, tot ACB in deser voughen:
Nemende AC voor hoochde, ende DG ende HB voor gronden, soo heeft den rechthouck begrepen onder AC ende DG, sulcken reden tot den rechthouck onder AC ende HB, ghelijck DG tot HB {I. v. 6. B. E.}; Maer ghelijck dien rechthouck tot desen, alsoo den driehouck ACD tot ACB, want elck driehouck is sijn rechthoucx helft {41. v. I. B. E.}, ghelijck dan DG tot HB, alsoo den driehouck ACD tot ACB.
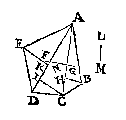
Des 5en voorbeelts bewys sal oock claer sijn als wy bewesen hebben, dat ghelijck EK met IC tot LM, alsoo den vierhouck ACDE tot den driehouck ACB, aldus:
Anghesien LM vierde euerednighe is der drie AD, AC, HB, de rechthouck begrepen onder AD ende LM, sal euen sijn {16. v. 6. B. E.} an den rechthouck begrepen onder AC ende HB, Laet ons nu EK, IC, LM, ansien voor gronden, wiens ghemeene hoochde AD;
|
![]() Y aldien de platten eenich ghewicht hadden, ende datmen toeliete die te wesen inde reden haerder grootheden, wy souden eyghentlick mueghen spreken van haer Swaerheydt, Swaerheyts middelpunt, Swaerheyts middellini, &c.
Y aldien de platten eenich ghewicht hadden, ende datmen toeliete die te wesen inde reden haerder grootheden, wy souden eyghentlick mueghen spreken van haer Swaerheydt, Swaerheyts middelpunt, Swaerheyts middellini, &c.
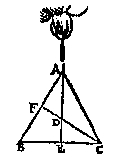 T' B E R E Y T S E L. Laet ghetrocken worden van A tot int middel van BC, de lini AE, sghelijcx van C tot int middel van AB, de lini CF.
T' B E R E Y T S E L. Laet ghetrocken worden van A tot int middel van BC, de lini AE, sghelijcx van C tot int middel van AB, de lini CF. 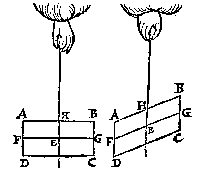 T' B E R E Y T S E L. Laet ghetrocken worden FG, tusschen de middelpunten van AD ende BC, insghelijcx HI, tusschen de middelpunten van AB ende DC.
T' B E R E Y T S E L. Laet ghetrocken worden FG, tusschen de middelpunten van AD ende BC, insghelijcx HI, tusschen de middelpunten van AB ende DC. 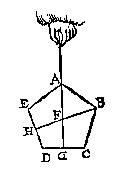 T' B E W Y S. Wesende den vijfhouck opghehanghen byde lini AG, het deel AGDE sal euewichtich hanghen teghen het deel AGCB, want sy sijn euegroot, ghelijck, ende van ghelijcker ghestalt: AG dan is swaerheyts middellini des vijfhoucx, ende om de selue reden sal BH oock des selfden vijfhoucx swaerehyts middellini wesen; maer dese doorsnien malcanderen in des formens middelpunt F, ende elck dier linien heeft in haer het swaerheyts middelpunt, tis dan F.
T' B E W Y S. Wesende den vijfhouck opghehanghen byde lini AG, het deel AGDE sal euewichtich hanghen teghen het deel AGCB, want sy sijn euegroot, ghelijck, ende van ghelijcker ghestalt: AG dan is swaerheyts middellini des vijfhoucx, ende om de selue reden sal BH oock des selfden vijfhoucx swaerehyts middellini wesen; maer dese doorsnien malcanderen in des formens middelpunt F, ende elck dier linien heeft in haer het swaerheyts middelpunt, tis dan F. 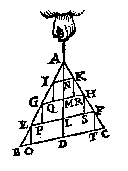 T' B E W Y S. Ouermits EF euewydighe is van BC, ende EO, FT met LD, soo sal EFTO, euewydich vierhouck sijn, wiens EL euen is met LF, oock met OD ende DT, waer duer het swaerheyts middelpunt des vierhoucx EFTO in DL is, duer het Ie voorstel deses boucx. Ende om de selue reden sal het swaerheyts middelpunt des euewydichs vierhoucx GHSP wesen in LM, ende van IKRQ in MN, ende vervolghens het swaerheyts middelpunt der form IKRHSFTOEPGQ ghemaect vande voornoemde drie vierhoucken, sal wesen inde lini ND, ofte AD.
T' B E W Y S. Ouermits EF euewydighe is van BC, ende EO, FT met LD, soo sal EFTO, euewydich vierhouck sijn, wiens EL euen is met LF, oock met OD ende DT, waer duer het swaerheyts middelpunt des vierhoucx EFTO in DL is, duer het Ie voorstel deses boucx. Ende om de selue reden sal het swaerheyts middelpunt des euewydichs vierhoucx GHSP wesen in LM, ende van IKRQ in MN, ende vervolghens het swaerheyts middelpunt der form IKRHSFTOEPGQ ghemaect vande voornoemde drie vierhoucken, sal wesen inde lini ND, ofte AD. 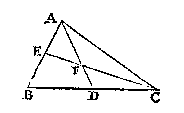 T' W E R C K. Men sal van A tot int middel van BC, trecken de lini AD, sghelijcx van C tot int middel van AB, de lini CE, sniende AD in F: Ick seg dat F t'begheerde swaerheydts middelpunt is.
T' W E R C K. Men sal van A tot int middel van BC, trecken de lini AD, sghelijcx van C tot int middel van AB, de lini CE, sniende AD in F: Ick seg dat F t'begheerde swaerheydts middelpunt is.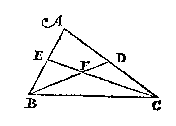 T' B E G H E E R D E. Wy moeten bewysen dat CF dobbel is an FE.
T' B E G H E E R D E. Wy moeten bewysen dat CF dobbel is an FE.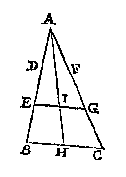 T' B E G H E E R D E. Wy moeten bewysen dat EG duer des driehoucx ABC swaerheyts middelpunt streckt
T' B E G H E E R D E. Wy moeten bewysen dat EG duer des driehoucx ABC swaerheyts middelpunt streckt T' W E R C K. Men sal den vierhouck deelen in twee driehoucken met de lini AC, ende vinden het swaerheyts middelpunt van elck driehouck, duer het 3e voorstel, dat van ACB sy E, ende van ACD sy F, ende de lini EF sal balck wesen. Daer naer salmen maken {Doorhe45.v.I.B.E.} twee euewydighe vierhoucken van een selfde hoogde, als GHIK, euen anden driehouck ACD, ende GHLM, euen anden driehouck ACB, daer naer deelende den balck {Door het 10.v.6.B.E.} FE in N, alsoo dat den erm NE, sulcken reden hebbe tot den erm NF, als HI tot HL; Ick seg dat N t'begheerde swaerheyts middelpunt is.
T' W E R C K. Men sal den vierhouck deelen in twee driehoucken met de lini AC, ende vinden het swaerheyts middelpunt van elck driehouck, duer het 3e voorstel, dat van ACB sy E, ende van ACD sy F, ende de lini EF sal balck wesen. Daer naer salmen maken {Doorhe45.v.I.B.E.} twee euewydighe vierhoucken van een selfde hoogde, als GHIK, euen anden driehouck ACD, ende GHLM, euen anden driehouck ACB, daer naer deelende den balck {Door het 10.v.6.B.E.} FE in N, alsoo dat den erm NE, sulcken reden hebbe tot den erm NF, als HI tot HL; Ick seg dat N t'begheerde swaerheyts middelpunt is.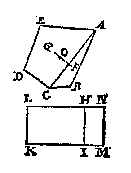 T' G H E G H E V E N. Laet ABCDE een ongheschickt vijfhouck sijn.
T' G H E G H E V E N. Laet ABCDE een ongheschickt vijfhouck sijn.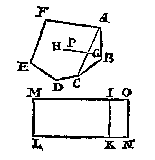 T' G H E G H E V E N. Laet ABCDEF een ongheschickt seshouck sijn.
T' G H E G H E V E N. Laet ABCDEF een ongheschickt seshouck sijn.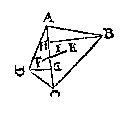 T' W E R C K. Men sal den vierhouck deelen in twee driehoucken, met de lini AC, ende vinden t'swaerheydts middelpunt van elcken driehouck door het 3e voorstel, dat van ACB sy E, ende vanden driehouck ACD sy F, de lini dan EF is balck. Daer naer salmen trecken DG ende BH, beyde rechthouckich op AC, deylende den balck FE en I, alsoo dat den erm IE, sulcken reden hebbe tot den erm IF, als DG tot BH; Ick seg dat I t'begheerde swaerheyts middelpunt is.
T' W E R C K. Men sal den vierhouck deelen in twee driehoucken, met de lini AC, ende vinden t'swaerheydts middelpunt van elcken driehouck door het 3e voorstel, dat van ACB sy E, ende vanden driehouck ACD sy F, de lini dan EF is balck. Daer naer salmen trecken DG ende BH, beyde rechthouckich op AC, deylende den balck FE en I, alsoo dat den erm IE, sulcken reden hebbe tot den erm IF, als DG tot BH; Ick seg dat I t'begheerde swaerheyts middelpunt is.  T' W E R C K. Men sal den vijfhouck deelen in drie driehoucken, met eenighe linien als AD, AC, vindende daer naer het swaerheyts middelpunt des vierhoucx ACDE duer het 4e voorbeelt, t'welck F sy, ende des driehoucx ACB duer het 3e voorstel, t'welck G sy, ende de lini FG, is balck, Daer naer ghetrocken BH rechthouckich op AC; Ende CI met EK rechthouckich op AD, men sal der drie linien AD, AC, HB, vinden de vierde euerednighe {Proportionalis.}, welcke sy LM, deelende den balck {Door het 12. v. 6. B. E.} FG in N, alsoo dat den erm NG sulcken reden hebbe tot den erm NF, ghelijck CI met EK, tot LM; Ick seg dat N het begheerde swaerheydts middelpunt is.
T' W E R C K. Men sal den vijfhouck deelen in drie driehoucken, met eenighe linien als AD, AC, vindende daer naer het swaerheyts middelpunt des vierhoucx ACDE duer het 4e voorbeelt, t'welck F sy, ende des driehoucx ACB duer het 3e voorstel, t'welck G sy, ende de lini FG, is balck, Daer naer ghetrocken BH rechthouckich op AC; Ende CI met EK rechthouckich op AD, men sal der drie linien AD, AC, HB, vinden de vierde euerednighe {Proportionalis.}, welcke sy LM, deelende den balck {Door het 12. v. 6. B. E.} FG in N, alsoo dat den erm NG sulcken reden hebbe tot den erm NF, ghelijck CI met EK, tot LM; Ick seg dat N het begheerde swaerheydts middelpunt is.
 T' W E R C K. Men sal den seshouck deelen in vier driehoucken, met eenighe linien als AC, AD, FD, vindende daer naer het swaerheyts middelpunt des vierhoucx ADCB door het 4e voorbeelt, t'welck G sy, ende des vierhoucx ADEF, t'welck H sy, ende de lini HG is balck. Daernaer ghetrocken BI ende DK rechthouckich op AC, insghelijcx AL ende EM beyde rechthouckich op FD, men sal der drie linien welcker eerste FD, de tweede AC, de derde BI met KD, vinden de vierde euerednighe, welcke NO sy, deelende den balck HG in P, also dat den erm PG, sulcken reden hebbe tot den erm PH, ghelijck AL met EM, tot NO; Ick seg dat P het begheerde swaerheyts middelpunt is.
T' W E R C K. Men sal den seshouck deelen in vier driehoucken, met eenighe linien als AC, AD, FD, vindende daer naer het swaerheyts middelpunt des vierhoucx ADCB door het 4e voorbeelt, t'welck G sy, ende des vierhoucx ADEF, t'welck H sy, ende de lini HG is balck. Daernaer ghetrocken BI ende DK rechthouckich op AC, insghelijcx AL ende EM beyde rechthouckich op FD, men sal der drie linien welcker eerste FD, de tweede AC, de derde BI met KD, vinden de vierde euerednighe, welcke NO sy, deelende den balck HG in P, also dat den erm PG, sulcken reden hebbe tot den erm PH, ghelijck AL met EM, tot NO; Ick seg dat P het begheerde swaerheyts middelpunt is.