Home | Stevin | < Deursichtighe
Anden Leser , Cortbegryp , bepalingen , begeerten , vlakke spiegel , bolvormige , Anhang
[ ]
T W E E D E
B O V C K D E R
D E V R S I C H T I G H E,
V A N D E
B E G H I N S E L E N D E R
S P I E G H E L S C H A E V W E N.
[ ]
Anden Leser.
 L S O ick my eens begaf tottet ondersoucken vande eyghenschappen der spieghelschaeuwen, beschreven door Alhazen en Vitello, en dat ick int bewijs van veel cromvlackige voorstellen geen seker besluyt en merckte, oock metter daet deur sommighe spieghelsche ervaringhen, daer in openbaerlick fauten bevant:
L S O ick my eens begaf tottet ondersoucken vande eyghenschappen der spieghelschaeuwen, beschreven door Alhazen en Vitello, en dat ick int bewijs van veel cromvlackige voorstellen geen seker besluyt en merckte, oock metter daet deur sommighe spieghelsche ervaringhen, daer in openbaerlick fauten bevant:
Soo ghevouchde ick my na sekerder gront te trachten, welcke ick na mijn meyning becommen hebbende, en ghevonden dat Euclides 17 en 18 voorstel *), met der gelijcke van Alhazen en Vitello als gront van veel ander voorstellen der cromvlackighe spieghelschaeuwen t'samen ghemist waren, ick schickte die by malcander beginselsche wijse.
Daer na sijn V O R S T E L I C K E G H E N A D E tot kennis der spieghelschaeuwen begheerich sijnde, ick en heb hem om de voorgaende redenen tottet deurgronden der boucken vande voorseyde schrijvers niet connen raden: Sulcx dat wy in die plaets dese beginselen namen: welcke int overlesen deur het nau ondersouck van sijn V O R S T E L I C K E G H E N A D E noch verbetering crijghende, sijn eyntlick ter form gherocht en onder sijn W I S C O N S T I G H E G H E D A C H T E N I S S E N vervought als volght.
[ *) Euclidis optica & catoptrica, Par. 1557 (ed. J. Pena), p. 55.]
C O R T B E G R Y P.
{Argumentum.}
 A 7 bepalinghen {Definitiones.} en 2 begheerten {Postulata.} sullen volghen 9 voorstellen: Achter welcke een Anhang {Appendix.} sal vervought sijn, inhoudende strijdinghen {Argumentationes.} die wy na ons ghemeene wijse mette leering niet en willen vermenghen.
A 7 bepalinghen {Definitiones.} en 2 begheerten {Postulata.} sullen volghen 9 voorstellen: Achter welcke een Anhang {Appendix.} sal vervought sijn, inhoudende strijdinghen {Argumentationes.} die wy na ons ghemeene wijse mette leering niet en willen vermenghen.
[ 95 ]
B E P A L I N G H E N.
{Definitiones.}
I B E P A L I N G.
Beginselen der spieghelschaeuwen sijn die, welcke de redenen verclaren vande formen der schaeuwen, veroirsaeckt deur der lichamen teghenwoordicheyt voor spieghels.
2 B E P A L I N G.
Alle wisconstighe vlacken {Mathematicæ superficies.} in welcke men sich voorstelt al ofter spieghelicke ghedaente in bestonde, heeten wy spieghels.
 A T V E R L I C K sprekende meugen alle blinckende vlacken als van glas, stael, water en dierghelijcke, voor spieghels ghehouden worden, Maer in desen wisconstighen handel stellen wy ons wisconstighe vlacken voor, die hier voor spieghels nemende. De selve ontfanghen na de ghemeene manier van ander saken, een naem na de ghestalt haerder form, als plat wesende, sy heet platspieghel; maer clootvlack, kegelvlack of seulvlack sijnde, alsdan clootspieghel, keghelspieghel, seulspieghel. Voort is bolle spieghel {Speculum Convexum.}, diens blinckende ghedaente genomen wort te staen op de bolle sijde, en holle spieghel {Concavum.}, diens blinckende ghedaente genomen wort op de holle sijde te wesen.
A T V E R L I C K sprekende meugen alle blinckende vlacken als van glas, stael, water en dierghelijcke, voor spieghels ghehouden worden, Maer in desen wisconstighen handel stellen wy ons wisconstighe vlacken voor, die hier voor spieghels nemende. De selve ontfanghen na de ghemeene manier van ander saken, een naem na de ghestalt haerder form, als plat wesende, sy heet platspieghel; maer clootvlack, kegelvlack of seulvlack sijnde, alsdan clootspieghel, keghelspieghel, seulspieghel. Voort is bolle spieghel {Speculum Convexum.}, diens blinckende ghedaente genomen wort te staen op de bolle sijde, en holle spieghel {Concavum.}, diens blinckende ghedaente genomen wort op de holle sijde te wesen.
Maer om t'voorgaende by gheteyckende formen opentlicker te verclaren, laet in elck deser drie formen de linien AB spieghels beteyckenen, d'eerste plat, overcant ghesien, de tweede een bolle clootspieghel, te weten bol over de sijde C; en de derde een holle clootspieghel, te weten hol over de sijde C.
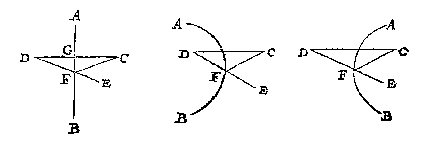
3 B E P A L I N G.
Verschaeulickpunt {Spectatum.} is diens schaeu {Simulacrum Imago.} genomen wort in een spieghel te connen verschijnen.
Laet inde drie formen der 2 bepaling, gheteyckent worden voor yder spiegel het punt C, diens schaeu inde spieghel wy nemen te sijn D. Nu want dit punt C aldus ghenomen wort in een spiegel te connen verschijnen, of verschaeut worden, soo heetet verschaeulickpunt.
[ 96 ]
4 B E P A L I N G.
Oogh is t'punt datmen neemt des oogs sienlick werck te doen.
Laet inde drie formen der 2 bepaling, gheteyckent worden t'punt E, t'welck wy nemen des ooghs sienlick werck te doen, namelick te sien D schaeu des verschaeulickpunts C: Dit soo sijnde, dat punt E heet oogh.
5 B E P A L I N G.
Ooghstrael, en verschaeulick puntstrael, sijn de rechte linien vant oogh en verschaeulickpunt totte schaeu.
Laet inde drie formen der 2 bepaling gheteyckent worden de rechte linien ED, CD: T'welck soo sijnde, de lini ED vant oogh E totte schaeu D, heet ooghstrael, En vant verschaeulickpunt C totte selve schaeu D, verschaeulickpunts strael.
6 B E P A L I N G.
Keerpunt is de ghemeene sne des spieghels en ooghstraels.
Laet inde drie formen der 2 bepaling de ghemeene sne des spieghels AB, en des ooghstraels ED, gheteyckent worden met F: T'selve punt F wort keerpunt gheseyt. D'oirsaeck des naems sal inde volghende 7 bepaling breeder verstaen worden.
7 B E P A L I N G.
Keerlijnen {Lineæ refractæ.} sijn de twee rechte van t'keerpunt tottet oogh en verschaeulick punt: Die na t'oogh streckt heet eyghentlick ooghkeerlijn, d'ander verschaeulickpunts keerlijn.
Laet inde drie formen der 2 bepaling, ghetrocken worden de rechte lini FC: T'welck soo sijnde, de twee linien FC, FE, vant keerpunt F, tottet oogh E, en tottet verschaeulickpunt C, heeten keerlijnen, welcker FE van t'keerpunt F tottet oogh E, heet ooghkeerlijn: En van F, tottet verschaeulickpunt C, verschaeulickpunts keerlijn.
Maer om d'oirsaeck des naems te verclaren, ick segh aldus: Ghelijck een bal gheworpen sijnde van C af, teghen de spieghel AB opt punt F, weerom can botten en te rugh keeren tot E, Also schijnt het verschaeulickpunt C, int ansien des ooghs E, sijn schaeu te worpen opt punt F, en van daer te keeren tottet oogh E: En van weghen sulcke ghelijckheyt wort FE, om datse van F na t'oogh keert, Ooghkeerlijn gheheeten. En om der ghelijcke redenen heet FC verschaeulickpunts keerlijn: En daerom oock F keerpunt.
[ 97 ]
B E G H E E R T E N.
{Postulata.}
I B E G H E E R T E.
Verschijnende t'verschaeulickpunt voor een platspieghel, wy begheeren toeghelaten te worden dattet even soo wijt vanden spieghel is als sijn schaeu: Oock het verschaeulickpunts strael op de spieghel rechthouckich te wesen.
Laet G in de platspieghel AB der 2 bepaling, de ghemeene sne sijn des selven spieghels en des verschaeulickpunts strael DC: Daer wort begeert datmen toelate GC even te wesen an GD, oock dat DC op AB rechthouckich is: En die hier af deur dadelicke ervaring meerder sekerheyt begheerde, soude meugen de verheyt des schaeus meten deur twee standen {Stationes.}, ghelijck men de ongherakelicke langden meet na de manier des 2 voorstels vant 2 bouck der Meetdaet {Praxis Geometricæ.}.
Angaende dattet verschaeulickpunts strael rechthouckich op de platspieghel comt dat canmen dadelick soo bevinden, met sijn oogh voor verschaeulickpunt te nemen, en des selfden ooghs schaeu te sien overcommen langs de sijde eens winckelhaecx, die op de platspieghel rechthouckich is.
2 B E G H E E R T E.
Mette ghemeene sne des spieghelvlacx, en des plats daer t'verschaeulickpunt, de schaeu en het oogh in sijn, verstaen te worden de ghegheven spieghel.
Laet de lini AB inde 2 bepaling, wesen de ghemeene sne des spieghelvlacx en des plats daer de drie punten C, D, E, in sijn: Daer wort begeert datmen met sulcken beschreven lijn AB de spieghel verstaen sal.
N V D E
V O O R S T E L L E N.
{Propositiones.}
I W E R C K S T I C K. I V O O R S T E L.
{Problema.}
Wesende ghegheven een oneyndelicke platspieghel, en een verschaeulickpunt: Sijn schaeu te vinden.
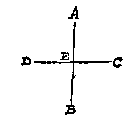
T G H E G H E V E N. Laet AB een oneyndelicke platspieghel sijn, ende C een verschaeulickpunt daer voor.
T B E G H E E R D E. Wy moeten sijn schaeu vinden.
T W E R C K.
Men sal trecken de lijn CD rechthouckich op AB, snyende de selve in E, ende alsoo dat ED even sy an EC: Ick segh
[ 98 ]
t'punt D de begheerde schaeu te sijn, waer af t'bewijs deur d'eerste begheerte openbaer is.
T B E S L V Y T. Wesende dan ghegheven een oneyndelicke platspieghel, en een verschaeulickpunt, wy hebben sijn schaeu ghevonden na den eysch.
V E R V O L G H.
Anghesien de lijn uyt oneyndelicke menichte van punten bestaet, ende dat de schaeu van yder dier punten ghevonden wort deur t'boveschreven 1 voorstel;
 Soo volght dat de beschrijving des schaeus van alle lijn in een platspieghel bekent is. Laet tot voorbeelt AB een platspieghel sijn, ende CD een cromme lijn met oneyndelicke menichte van punten daer in gheteeckent als C, E, F, G, D: Nu ghevonden haer schaeuwen H, I, K, L, M, alsboven, de lijn ghetrocken deur sulcke oneyndelicke menichte van punten als de lijn HIKLM, is de begheerde schaeu.
Soo volght dat de beschrijving des schaeus van alle lijn in een platspieghel bekent is. Laet tot voorbeelt AB een platspieghel sijn, ende CD een cromme lijn met oneyndelicke menichte van punten daer in gheteeckent als C, E, F, G, D: Nu ghevonden haer schaeuwen H, I, K, L, M, alsboven, de lijn ghetrocken deur sulcke oneyndelicke menichte van punten als de lijn HIKLM, is de begheerde schaeu.
Voort anghesien yder lichaems vlack, uyt oneyndelicke menichte van linien bestaet, ende yder lichaem in vlacken begrepen is, soo volght uyt redenen alsvooren, dat de beschrijving des schaeus van yder lichaem in een platspieghel oock openbaer is.
2 W E R C K S T I C K. 2 V O O R S T E L.
Wesende ghegheven een oneyndelicke platspieghel, met een verschaeulickpunt en t'oogh: T'keerpunt te vinden.
T G H E G H E V E N. Laet AB een oneyndelicke platspieghel sijn, C t'verschaeulickpunt, ende D het oogh.
T B E G H E E R D E. Wy moeten t'keerpunt vinden.
T W E R C K.
 Men sal vinden de schaeu van C, als E, deur het 1 voorstel, dat is treckende de lini CE rechthouckich op AB, snyende de selve in F, ende also dat FE even sy an FC, daer na de rechte ED, snyende AB in G, welcke sne G ick segh t'begheerde keerpunt te wesen.
Men sal vinden de schaeu van C, als E, deur het 1 voorstel, dat is treckende de lini CE rechthouckich op AB, snyende de selve in F, ende also dat FE even sy an FC, daer na de rechte ED, snyende AB in G, welcke sne G ick segh t'begheerde keerpunt te wesen.
T B E W Y S.
Angesien E de schaeu is des verschaeulickpunts C deur het 1 voorstel, ende D oogh deur t'ghegheven, soo is ED ooghstrael deur de 5 bepaling, en daerom G keerpunt deur de 6 bepaling.
T B E S L V Y T. Wesende dan ghegheven een oneyndelicke platspieghel met een verschaeulickpunt, en t'oogh; Wy hebben t'keerpunt ghevonden nae den eysch.
[ 99 ]
I V E R T O O C H. 3 V O O R S T E L.
T'verschaeulickpunt en sijn schaeu, staen evewijt vant oneyndelick plat des voortghetrocken platspieghels.
T G H E G H E V E N. Laet AB een platspieghel sijn, wiens oneyndlick voortghetrocken plat CD is, ende E sy een verschaeulickpunt, alsoo dat de lijn EF rechthouckich op CD, niet en streckt deur de spieghel AB, ende EF snye CD in G.
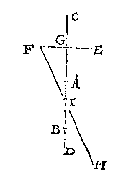 T B E R E Y T S E L. Laet ghenomen worden CD teenemael een platspieghel te wesen, ende eenich oogh ghestelt worden als H siende de schaeu F deur t'keerpunt I inde spieghel AB.
T B E R E Y T S E L. Laet ghenomen worden CD teenemael een platspieghel te wesen, ende eenich oogh ghestelt worden als H siende de schaeu F deur t'keerpunt I inde spieghel AB.
T B E W Y S.
Wesende CD aldus een platspieghel, ende F schaeu des verschaeulickpunts E, so sijn E ende F evewijt van G deur de I begheerte. Laet ons nu wech doen de spiegheldeelen AC ende BD, soo datter maer spieghel en blijve AB: T'welck so sijnde, het oogh H siet noch de schaeu F want blijvende t'keerpunt des spieghels I onverandert ende ongheroert, de wechdoening van al de rest des spieghels, en belettet oogh niet deur I t'punt F te sien: Maer de schaeu F van t'oogh H daer alsoo ghesien wesende, soo isse in die plaets niet teghenstaende tusschen E F geen spieghel en is, oock even soo wijt vant oneyndelick plat des voortghetrocken platspiegels, als sijn verschaeulickpunt E.
T B E S L V Y T. T'verschaeulickpunt en sijn schaeu dan, staen evewijt vant oneyndelick plat des voortghetrocken platspieghels, t'welck wy bewijsen moesten.
2 V E R T O O C H. 4 V O O R S T E L.
Des verschaeulickpunts keerlijn, ende d'oogh keerlijn, maken op den platspieghel even houcken.
T G H E G H E V E N. Laet AB een platspieghel sijn, ende C t'verschaeulickpunt, D de schaeu, CD verschaeulickpunts strael, snyende AB in E, ende F het oogh, DF ooghstrael; G keerpunt, GC verschaeulickpunts keerlijn, GF ooghkeerlijn.
T B E G H E E R D E. Wy moeten bewijsen dat den houck CGA, even is anden houck FGB.
T B E W Y S.
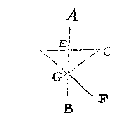 Anghesien EG rechthouckich op DC, ghemeene sijde is der driehoucken DEG, ende CEG, oock dat DE even is an EC deur de I begheerte, so is DG even an CG {26.v.I.b.E.}, voort is den houck CGE even anden houck DGE {15.v.I.b.E.}; Maer den houck FGB, is oock even anden houc DGE, daerom den houck CGE, is even anden houck FGB. Maer den houck CGE ofte CGA is al een selfde, daerom den houck CGA, is even anden houck FGB.
Anghesien EG rechthouckich op DC, ghemeene sijde is der driehoucken DEG, ende CEG, oock dat DE even is an EC deur de I begheerte, so is DG even an CG {26.v.I.b.E.}, voort is den houck CGE even anden houck DGE {15.v.I.b.E.}; Maer den houck FGB, is oock even anden houc DGE, daerom den houck CGE, is even anden houck FGB. Maer den houck CGE ofte CGA is al een selfde, daerom den houck CGA, is even anden houck FGB.
T B E S L V Y T. Des verschaeulickpunts keerlijn dan, ende d'ooghkeerlijn, maken op den platspieghel even houcken, t'welck wy bewijsen moesten.
[ 100 ]
3 V E R T O O C H. 5 V O O R S T E L.
Wesende een clootspieghel en verschaeulickpunt, van t'welck deur des clootspieghels middelpunt een oneyndelicke lini ghetrocken is: De schaeu in die lijn, en t'verschaeulickpunt, sijn evewijt vande clootspieghel.
{Teghen het 21 voorstel des 1 boucx ? van Euclides en sijn navolghers.}
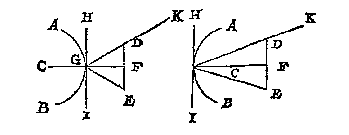
T G H E G H E V E N. Laet A B twee clootspiegels sijn, d'een bol, d'ander hol, diens middelpunt C is, ende D sy t'verschaeulickpunt, van t'welck deur C ghetrocken is, de oneyndelicke DE, snyende de spieghel in F.
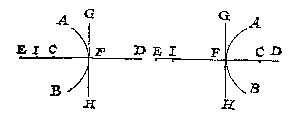
T B E G H E E R D E. Wy moeten bewijsen dat de schaeu inde lijn DE, even soo wijt is vande clootspieghel, dat is vant t'punt F, als t'verschaeulickpunt D.
T B E R E Y T S E L. Laet ghetrocken worden de platspiegel GH, deur t'punt F, ende rechthouckich op CF, daer na sy geteyckent t'punt I, alsoo dat IF even sy an FD.
T B E W Y S.
Anghesien CF rechthouckich is op GH, soo gheraeckt GH de lijn AB int punt F {28.v.3.b.E.}, daerom F is ghemeen punt des platspieghels ende clootspieghels, deur welck punt F het verschaeulickpunt D verschijnt; Daerom oock is de schaeu in d'een en d'ander spieghel op een selfde plaets: Maer de schaeu des platspieghels is I deur het 1 voorstel, de schaeu dan des clootspieghels is oock I: Maer I is inde platspieghel even soo wijt van t'punt F, als D, daerom de schaeu des clootspieghels AB, is even soo wijt vande clootspieghel, dat is van t'punt F, als sijn verschaeulickpunt D.
A N D E R B E W Y S.
Laet ons nemen dat de clootspieghel AB, recht ghetrocken worde tot inde platspieghel GH, alsoo datse beyde in een selve plat staen; t'welck soo wesende, I is ghemeene schaeu van d'een en d'ander spieghel des verschaeulickpunts D deur het 1 voorstel, ende F ghemeene sne der spieghels, met des verschaeulickpunts strael ID. Laet ons nu nemen dattet plat AB, blijvende t'punt F onverroerlick, weder ghecromt worde in sijn eerste clootsche ghestalt: Dit soo sijnde, de schaeu I is noch op haer selve plaets, want blijvende de punten F en D (die alleenlick des schaeus oirsaeck sijn, overmidts d'ander stof des spieghels buyten t'punt F, tot de saeck en gheeft noch en neemt) onverroert, soo moet de schaeu I inde clootspieghel oock op haer plaets onbeweeghlick blijven, dat is in sulcke wijde van F, alsser D af is.
T B E S L V Y T. Wesende dan een clootspiegel, en een verschaeulickpunt, van t'welck deur des clootspieghels middelpunt een oneyndelicke lijn ghetrocken is: de schaeu in die lijn en t'verschaeulickpunt, sijn evewijt vande clootspieghel t'welck wy bewijsen moesten.
[ 101 ]
M E R C K T.
Hier boven wort eyghentlick gheseyt vande schaeu inde lijn DE, want met al d'ander schaeuwen die inde clootspiegel van oneyndelicke menichte connen sijn, ist anders ghestelt, soo int volghende blijcken sal.
3 W E R C K S T I C K. 6 V O O R S T E L.
Wesende ghegheven een clootspieghel, t'verschaeulickpunt, en t'oogh t'welck de schaeu sien can: T'keerpunt te vinden.
Oogh dat de schaeu sien can, is diens rechte lijn tusschen t'oogh en t'verschaeulickpunt, den cloot niet en raeckt, noch daer deur en lijdt: Oock diens keerlijn op t'ghegheven deel des clootspieghels even houcken connen maken, en dat om bekende redenen.
I Voorbeelt alwaer t'verschaeulickpunt en het oogh, evewijt van t'middelpunt des clootspieghels sijn.
T G H E G H E V E N. Laet AB een clootspieghel wesen, diens middelpunt C is, en t'verschaeulickpunt sy D, maer het oogh E, welcke D ende E evewijt van t'middelpunt C sijn.
T B E G H E E R D E. Wy moeten t'keerpunt vinden.
T W E R C K.
Men sal trecken de lijn DE, ende uyt haer middel F, de lijn FC, snyende AB in G: t'welck soo sijnde, ick segh G t'begheerde keerpunt te wesen.
T B E R E Y T S E L. Laet ghetrocken worden GD, GE, voort HI, als platspieghel gherakende AB in t'punt G.
T B E W Y S.
Anghesien DF des driehoucx DFG, even is an FE des driehoucx EFG, ende haer ghemeene GF daer op rechthouckich, so is den driehouck DFG, even ende ghelijck an den driehouck EFG, daerom oock den houck DGF, even anden houck EGF: Voort, na dien HI den booch AB in G gheraeckt, soo is HI rechthouckich op GF: Daerom oock den houck FGH, even anden houck FGI: Nu van dese twee even houcken, ghetrocken de twee even houcken DGF, EGF, de blijvende houcken DGH ende EGI sijn oock even, ende vervolghens soo is G keerpunt des platspieghels HI deur het 2 voorstel: Maer G is ghemeen punt des clootspieghels AB, ende platspieghels HI, daerom de schaeu van D, welcke vant oogh E ghesien wort deur G des platspieghels,
[ 102 ]
de selve schaeu worter oock afghesien deur G des clootspieghels: G dan is oock keerpunt des clootspieghels AB, t'welck wy bewijsen moesten.
2 Voorbeelt, alwaer t'verschaeulickpunt ende het oogh, onevewijt van t'middelpunt des clootspieghels staen.
T G H E G H E V E N. Latet verschaeulickpunt nu inde boveschreven form K wesen, verder vant middelpunt des spieghels C, dant oogh E.
T B E G H E E R D E. Wy moeten t'keerpunt vinden.
M E R C K T.
Alsoo my hier af alsnu gheen wisconstighe manier te vooren en comt, wy sullent tuychwerckelick {Mechanicè.} doen in deser voughen.
T W E R C K.
Men sal trecken eenighe twee linien KG, EG, makende eenighen houck KGE, die t'begheerde soo na comt als uyt het oogh mach gheoirdeelt worden, daer na salmen deur t'punt G, trecken de lini CGF, welcke soo sy den houck KGE even in tween deelt, soo heeftmen t'begheerde keerpunt, dies niet, soo salmen de twee linien als KG, EG, trecken uyt een punt als G so veel opwaert of neerwaert, ende dat soo menichmael doen, tot dat soodanighe lini als CF, den houck ghelijck KGE, even in tween doorsnijt, twelck soo wesende t'bewijs is deur t'voorgaende openbaer.
4 W E R C K S T I C K. 7 V O O R S T E L.
Wesende ghegheven een clootspieghel, t'verschaeulickpunt, en het oogh dat de schaeu sien can: De schaeu te vinden.
T G H E G H E V E N. Laet AB een clootspieghel sijn, C t'verschaeulickpunt, D het oogh dat de schaeu sien can.
T B E G H E E R D E. Wy moeten de schaeu vinden.
T W E R C K.
Men sal eerst t'keerpunt vinden deur het 2 voorstel, t'welck E sy, treckende de rechte lijn FG, alsoo datse den booch AB gherake int punt E, daer na de lijn CH rechthouckich op FG, die snyende in I, ende alsoo, dat IC even sy an IH. Ick segh H de begheerde schaeu te wesen.
T B E W Y S.
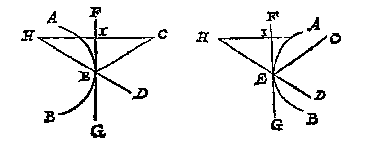
Anghesien FG den booch AB in E gheraeckt, soo is FG rechthouckich op des clootspiegels bedochte middellijn deur E, de selve middellijn soude den houck CED openbaerlick int middel deelen, daerom oock is den houck CEF, even anden houck DEG:
[ 103 ]
T'welck soo wesende, H is de schaeu des verschaeulickpunts C, inde platspieghel FG deur het 1 voorstel: Maar t'keerpunt E des platspieghels FG, is oock t'keerpunt des clootspieghels AB, daerom valt de schaeu van d'een en d'ander spieghel op een selve plaets, want by aldient op een ander viel, soo soude de stof des clootspieghels buyten E daer af d'oirsaeck moeten wesen; t'welck onmeughelick is, overmidts die tot de saeck en gheeft noch en neemt. H dan is de begheerde schaeu, t'welck wy bewijsen moesten.
T B E S L V Y T. Wesende dan ghegheven een clootspieghel t'verschaeulickpunt en t'oogh welck de schaeu sien can, Wy hebben de schaeu gevonden na den eysch.
5 W E R C K S T I C K. 8 V O O R S T E L.
Wesende ghegheven een spieghel van form soot valt, t'verschaeulickpunt en t'oogh, t'welck de schaeu sien can: T'keerpunt te vinden.
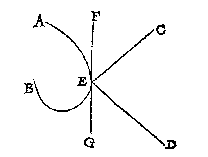
T G H E G H E V E N. Laet AB eenich cromvlackich spieghel sijn van form soot valt, C t'verschaeulickpunt en D het oogh.
T B E G H E E R D E. Wy moeten t'keerpunt vinden.
M E R C K T.
Alsoo my hier af (ghelijck oock vant 2 voorbeelt des 6 voorstels) gheen wisconstighe manier te vooren en comt, wy sullent tuychwerckelick {Mechanicè.} doen in deser voughen.
 T W E R C K.
T W E R C K.
Ick teycken inde spieghel AB eenich punt als E, ter plaets daer my uyter oogh dunckt het keerpunt te willen vallen, treck daer na deur t'selve punt E de lini FG als platspieghel, gherakende sonder snyen de spieghel AB, treck daer na EC en ED. By aldien, nu den houck CEF, even bevonden wort anden houck, DEG, soo is E t'begheerde keerpunt. Maer by aldien die twee houcken oneven bevonden wierden, men sal het punt als E hoogher of legher stellen tot dat sulcke twee houcken even vallen, t'welck ick neem te ghebeuren wesende dat punt an E: Dit soo sijnde ick segh E t'begheerde keerpunt te wesen.
T B E W Y S.
Anghesien de platspieghel FG, de cromvlackighe spieghel AB in t'punt E gheraeckt, soo is t'punt E ghemeen in d'een en d'ander spiegel, daerom de schaeu des verschaeulickpunts C, die vant oogh D ghesien wort deur E als keerpunt des platspieghels FG, de selve schaeu worter oock ghesien deur E als keerpunt des ghegheven cromvlackighe spieghels AB, en daerom is E oock keerpunt des selven spiegels AB, t'welck wy bewijsen moesten.
T B E S L V Y T. Wesende dan ghegheven een spieghel van form soot valt, t'verschaeulickpunt, en t'oogh t'welck de schaeu sien can, wy hebben t'keerpunt ghevonden, na den eysch.
[ 104 ]
6 W E R C K S T I C K. 9 V O O R S T E L.
Wesende ghegheven een spieghel van form soot valt, t'verschaeulicklickpunt, en het oogh t'welck de schaeu sien can: De schaeu te vinden.
T G H E G H E V E N. Laet AB eenich cromvlackich spieghel sijn van form soot valt, C t'verschaeulickpunt, D het oogh.
T B E G H E E R D E. Wy moeten de schaeu vinden.
T W E R C K.
Men sal eerst het keerpunt vinden deur het 8 voorstel t'welck E sy, en de lini die int vinden des selven punts E ghetrocken wort als platspieghel sy FG, daer na sy ghetrocken de lini CH rechthouckich op FG die snyende in I, also dat IC even sy an IH.
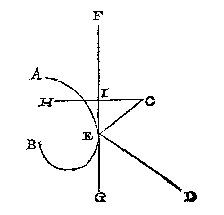 Dit soo wesende ick segh H de begheerde schaeu te wesen.
Dit soo wesende ick segh H de begheerde schaeu te wesen.
T B E W Y S.
Anghesien de platspieghel FG, de cromvlackighe spieghel AB int punt E gheraect, soo is t'punt E ghemeen in d'een en d'ander spiegel: Daerom de schaeu des verschaeulickpunts die vant oogh D ghesien wort deur E als keerpunt des platspieghels FG, de selve schaeu wort oock ghesien deur E als keerpunt des gegeven cromvlackighe spieghels AB, en daerom is H oock schaeu inde selve spiegel AB.
T B E S L V Y T. Wesende dan ghegeven een spieghel van form soot valt, t'verschaeulickpunt en het oogh t'welck de schaeu sien can, wy hebben de schaeu gevonden, na den eysch.
V E R V O L G H.
Wesende deur dit 9 voorstel openbaer de vinding des schaeus van yder verschaeulickpunt sienlick in een spieghel van form alst valt, soo volght oock in alle spiegel bekent te wesen de vinding des schaeus van yder lini, vlack en lichaem, te weten de lini deur oneyndelicke beschrijving van punten, en t'vlack deur beschrijving van linien, en t'lichaem deur beschrijving van vlacken.
[ 105 ]
A N H A N G.
Inhoudende dat de voorstellen van Euclides, Alhazen, en Vitello, met hun navolghers, leerende het vinden der schaeuwen in onplatte spieghels, ghemist sijn, als op ghemiste beginselen {Elementa.} ghegront wesende.
Met sulcke meyning als int begin des Anhangs ten eynde vant bouck der clootsche driehoucken vergaert sijn ander schrijvers fauten, mette selve meyning worden hier de volgende fauten beschreven. Om dan totte saeck te commen ick segh aldus.
De vinding vande ware plaets des schaeus, is een der voornaemste eynden deser const: De selve is inde platspieghels bycans als deur ghemeen wetenschap bekent, maer inde oneven spieghels niet alsoo, want Euclides int 17 en 18 voorstel [1557], Alhazen int 3, 6, ende 16 des 5 boucx, Vitello int 11 des 6 boucx [1572], hebben die schaeu inde clootspieghels gheraemt te wesen inde ghemeene sne des ooghstraels, ende des oneyndelicken rechten lijns, vant verschaeulickpunt deur des clootspieghels middelpunt, t'welck deur het 7 voorstel van desen ghemist is, alwaer die schaeu op een ander plaets wisconstlick {Mathematicè.} bethoont wort.
D'ervaring die hun bedrooch wort by voorbeelt aldus verclaert: Alsmen met beyde d'ooghen de schaeu sijns aensichts siet in een clootspieghel die recht voor t'aensicht staet; daer na in een platspiegel die even so wijt vant aensicht is, De schaeu inde clootspiegel ghelaet heur spiegelvlack naerder dan de schaeu inde platspieghel.
Om van t'welck sekerheyt te hebben, men sal nemen een cristalijnen platspiegel, hebbende inde canten van achter cleyne ronde putkens, die van vooren clootspieghelkens ghelaten, want soo worden de cristalijne platspieghels veel ghemeenlick ghemaeckt: Stellende, daer na die spieghel alsoo, dat het cleen schaeuken van een dier clootspieghelkens, passe op de nues des grooten schaeus inde platspieghel, men sal daetlick sien het cleen schaeuken naerder het vlack te wesen dan de groote schaeu, want soo verre sijn grootheyt streckt, soo bedecket de groote schaeu, waer af de contrari soude gebeuren soot verder waer. T'welck daer an noch sekerder is, dat alsmen siet na de schaeu sijns nuespunts int clootspieghelken, men ghevoelt daetlick datmen scheel siet, ende sijn gesichten meer na malcander keert, dan alsmen de schaeu sijns nuespunts inde platspieghel siet.
Daerom de twee linien streckende vande gesichten tot de schaeu des nuespunts inde clootspieghel, sijn binnen de twee linien streckende vande ghesichten tot de schaeu des nuespunts inde platspieghel: Waer uyt men besluyt dat de schaeu des nuespunts inde clootspieghel naerder heur spieghelvlack is dan de schaeu in de platspieghel, deur het 21 voorstel des 1 boucx van Euclides. Nu want hem dit dus uyterlick gheliet, hebben t'ghene soo scheen besloten soo te wesen.
Maer wy van t'een en t'ander beter voorsien, connen metter oirsaken kennis daer in voortvaren, versekert sijnde datter in d'ervaring, overmidts sy teghen de Wisconstighe beginselen strijt, bedroch is, t'welck aldus ontdeckt wort: Alsmen met beyde d'ooghen in een clootspieghel eenighe schaeu siet, ick neem de schaeu des voornoemden nuespunts inde ghestalt alsvooren, yder oogh siet deur een besonder keerpunt een eyghen nuespunts schaeu, te weten t'rechter oogh siet de schaeu ter slinckersijde, ende t'slincker oogh de schaeu ter rechter sijde, inder
[ 106 ]
voughen datmen deur twee verscheyden keerpunten twee verscheyden schaeuwen siet, die eyghentlick verder van d'ooghen staen, dan de ghemeen sne der stralen, ende nochtans in die sne der stralen een selfde schaeu schijnen te wesen.
Int ghene hier gheseyt is sijn twee saken t'anmercken, d'een datter twee schaeuwen sijn in verscheyden plaetsen, d'ander datse inde gemeen sne der stralen een selfde schaeu schijnen te wesen.
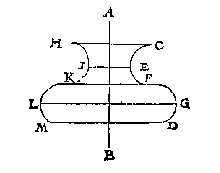
T'eerste blijckt daetlick aldus:
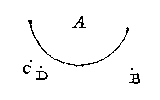 Neemt voor een bol clootspieghel als A, een brandende keers wiens vlam deur t'punt B beteeckent sy, in een camer sonder ander licht (tis wel waer datmen sulcx met eenich ander lichaem soude meughen doen voor een clootspieghel inden dach, maer wy hebben liever t'merckelickste voorbeelt te stellen) met de twee punten C, D, worden beyde d'ooghen beteeckent, welcke soo staen, dat D naerder de spieghel is dan C, inder voughen datmen sijn ooghen sal moeten keeren ende sijdeling naer de schaeuwen sien.
Neemt voor een bol clootspieghel als A, een brandende keers wiens vlam deur t'punt B beteeckent sy, in een camer sonder ander licht (tis wel waer datmen sulcx met eenich ander lichaem soude meughen doen voor een clootspieghel inden dach, maer wy hebben liever t'merckelickste voorbeelt te stellen) met de twee punten C, D, worden beyde d'ooghen beteeckent, welcke soo staen, dat D naerder de spieghel is dan C, inder voughen datmen sijn ooghen sal moeten keeren ende sijdeling naer de schaeuwen sien.
De voornoemde brandende keers salmen inde rechterhant houden over d'een sijde des spieghels, brenghende beyde d'ooghen C D neven de spieghel over d'ander sijde, maer alsoo, dat beyde de schaeuwen des vlams B, niet en sijn int plat {Plano.} deur beyde d'ooghen C, D, t'welck deur verheffing of daling des keers licht gheschien can. Dit soo wesende, men sal daetlick beyde de verscheyden schaeuwen des vlams sien.
D'oirsaeck waerom men die deur scheel te sien niet op malcander en can brenghen, ghelijckt ghebeurt alsmen recht na de clootspieghel siet, is datse met d'ooghen niet in een selfde plat en sijn, ende dat de verroering der ooghen int scheelsien alleenlick in een selfde plat ghebeurt, want de natuer en heeftet soo niet gevoucht, dattet een oogh opwaert can sien t'ander neerwaert.
Wy hebben dan bethoont datter met twee ooghen inde clootspieghel twee verscheyden schaeuwen ghesien worden. Daer rest noch dadelick te bewijsen datse inde ghemene sne der stralen een selfde schaeu schijnen te wesen aldus:
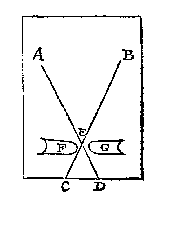
Men sal opt eynde eens tafels twee evenhooghe brandende keersen stellen, ontrent een duym of twee lanck, in een camer sonder licht. Deser keersen vlammen sijn beteeckent met de punten A, B: Daer na salmen stellen ande cant vant ander eynde des tafels twee punten C, D, van malcander soo wijt als des ondersouckers ghesichten d'een van d'ander staen, treckende daer na de linien of stralen AD, ende BC, malcander snyende in E, men sal in die ghemeen sne E een spelt of naelde recht overeynde steken, stellende inden houck AEC eenich schutsel, ick neem een bouck F over eynde staende, alsoo dat het oogh an C de vlam A niet sien en can, maer alleenlick de vlam B. S'ghelijcx een bouck G, inden houck BED, inder voughen dat het oogh an D, de vlam B niet sien en can, maer alleenlick de vlam A.
Dit so bereyt wesende, men sal sien na de spel die an E ghesteken was, t'welck doende beyde de vlammen A, B, schijnen een selfde vlam, ende dat segh ick ter plaets van E, want alle strael, ofte lijn van t'ghesicht tottet ghesien, is deur gemeen wetenschap recht, daerom de vlam A en can ant oogh D niet schijnen buyten de lijn AD, noch de vlam B, ant oogh C, buyten de lijn BC, Maer dese twee lijnen en vergaren nerghens dan in E, daerom is E d'eyghen plaets van sulck schijnsel.
Even eens gadet in ons voorbeelt der clootspieghels toe, want ghelijck twee vlammen hier een vlam ghelaten, tot een ander plaets dan de ware, alsoo schijnen
[ 107 ]
daer twee schaeuwen een schaeu te wesen, tot een ander plaets als de warachtighe.
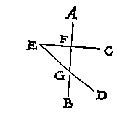
Maer om t'selve deur voorbeelt in clootspiegels noch claerder te maken, laet A, B, clootspiegels sijn, d'een bol, d'ander hol, diens middelpunt C is, D, E, twee ooghen, F t'nuespunt, G t'keerpunt van FE, ende H t'keerpunt van FD, ende IK een platspieghel gherakende den clootspiegel int punt G, ende FL sy rechthouckich op KI, oock alsoo dat IL even sy an IF: t'welck soo wesende L is schaeu des verschaeulickpunts F ghesien vant oogh E deur het 7 voorstel deser beginselen ende FL verschaeulickpunts strael, maer LE ooghstrael, deur de 5 bepaling.
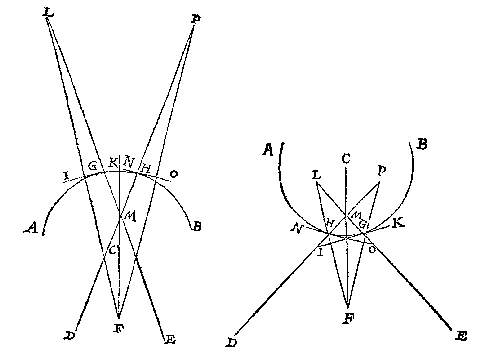
Laet nu ghetrocken worden de lijn deur C F snyende LE in M, ende NO als platspieghel gherakende den clootspieghel in H, ende FP rechthouckich op ON, alsoo dat OF even sy an OP. Dit soo wesende P is de schaeu des verschaeulickpunts F ghesien vant oogh D, ende FP verschaeulickpunts strael, PD ooghstrael snyende de middellijn die deur CF streckt oock in M.
Nu merct op den sin: L, P, sijn twee schaeuwen, welcke om de boveschreven redenen in M bedriechlick schijnen te staen ende daer een schaeu te wesen, daerom oock hebben sy bedroghen sijnde ghemeent M de ware plaets des schaeus te wesen, dat is (ghelijck wy boven gheseyt hebben hun voorstellen in te houden) de ghemeene sne des ooghstraels LE, en des rechten lijns van t'verschaeulickpunt F deur des clootspiegels middelpunt C, waer mede d'oirsaeck der d'waling grontlick verclaert is, want uyt de voorseyde 3, 6, ende 16 voorstellen der bolle ende holle clootspieghels van Alhazen in sijn 5 bouck, sijn oock beschreven der gelijcke van bolle ende holle pylaerspieghels ende keghelspieghels, te weten inde 4, 7, 8, en 10, voorstellen des selfden 5 boucx, die Vitello int 36 ende 37 voorstel sijns 5 boucx vervaet, welcke altemael gedwaelde beginselen sijn daer een groote menichte van ghedwaelde voorstellen uyt ghesproten is, als onder anderen de ghene die daer handelen van schaeuwen buyten de spiegels inde locht, t'welck [deur]
[ 108 ]
door ander bekende oirsaken ghebeurt dan sy stellen, daer af wy een andermael inde spiegheldaet misschien handelen sullen.
Angaende dat de schaeu van F inde holclootspieghel hier boven bedriechlick in M schijnt te staen, t'welck buyten de spiegel is tusschen de oogen ende t'spieghelvlack, waer uyt ymant dencken mocht dat sy wetens sulck schijnsel voor t'warachtighe ghenomen hebben, maer tis anders daer mede ghestelt, want alsmen na t'inhout haerder voorstellen de schaeu met een oogh siet, soo is sulck bedriechlick ghelaet gheweert. Ende oftmen al schoon met twee ooghen saghe, soo en can sulck ghelaet van schaeu achter t'gesicht niet sijn, of elders inde locht, alsoo dat de spieghel niet recht achter die schijnende schaeu en sta ghelijck sy besluyten.
In somme de voorstellen der bolle ende holle clootspieghels, pylaerspiegels, ende keghelspiegels handelende van der schaeuwen plaets soo wel binnen als buyten de spieghels sijn gemist, ende dat overmidts sy, ghelijck wy in desen Anhang bewijsen wilden, op ghemiste beginselen ghegrondet sijn.*)
D E S T W E E D E N B O V C X
E Y N D E.
[ *) Enkele opmerkingen hierover in Isack Beeckman, Journal, II, p. 405.]
Home | Simon Stevin | Deursichtighe | Spieghelschaeuwen (top)
 L S O ick my eens begaf tottet ondersoucken vande eyghenschappen der spieghelschaeuwen, beschreven door Alhazen en Vitello, en dat ick int bewijs van veel cromvlackige voorstellen geen seker besluyt en merckte, oock metter daet deur sommighe spieghelsche ervaringhen, daer in openbaerlick fauten bevant:
L S O ick my eens begaf tottet ondersoucken vande eyghenschappen der spieghelschaeuwen, beschreven door Alhazen en Vitello, en dat ick int bewijs van veel cromvlackige voorstellen geen seker besluyt en merckte, oock metter daet deur sommighe spieghelsche ervaringhen, daer in openbaerlick fauten bevant: 
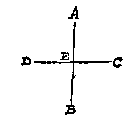
 Soo volght dat de beschrijving des schaeus van alle lijn in een platspieghel bekent is. Laet tot voorbeelt AB een platspieghel sijn, ende CD een cromme lijn met oneyndelicke menichte van punten daer in gheteeckent als C, E, F, G, D: Nu ghevonden haer schaeuwen H, I, K, L, M, alsboven, de lijn ghetrocken deur sulcke oneyndelicke menichte van punten als de lijn HIKLM, is de begheerde schaeu.
Soo volght dat de beschrijving des schaeus van alle lijn in een platspieghel bekent is. Laet tot voorbeelt AB een platspieghel sijn, ende CD een cromme lijn met oneyndelicke menichte van punten daer in gheteeckent als C, E, F, G, D: Nu ghevonden haer schaeuwen H, I, K, L, M, alsboven, de lijn ghetrocken deur sulcke oneyndelicke menichte van punten als de lijn HIKLM, is de begheerde schaeu.  Men sal vinden de schaeu van C, als E, deur het 1 voorstel, dat is treckende de lini CE rechthouckich op AB, snyende de selve in F, ende also dat FE even sy an FC, daer na de rechte ED, snyende AB in G, welcke sne G ick segh t'begheerde keerpunt te wesen.
Men sal vinden de schaeu van C, als E, deur het 1 voorstel, dat is treckende de lini CE rechthouckich op AB, snyende de selve in F, ende also dat FE even sy an FC, daer na de rechte ED, snyende AB in G, welcke sne G ick segh t'begheerde keerpunt te wesen. T B E R E Y T S E L. Laet ghenomen worden CD teenemael een platspieghel te wesen, ende eenich oogh ghestelt worden als H siende de schaeu F deur t'keerpunt I inde spieghel AB.
T B E R E Y T S E L. Laet ghenomen worden CD teenemael een platspieghel te wesen, ende eenich oogh ghestelt worden als H siende de schaeu F deur t'keerpunt I inde spieghel AB. Anghesien EG rechthouckich op DC, ghemeene sijde is der driehoucken DEG, ende CEG, oock dat DE even is an EC deur de I begheerte, so is DG even an CG {26.v.I.b.E.}, voort is den houck CGE even anden houck DGE {15.v.I.b.E.}; Maer den houck FGB, is oock even anden houc DGE, daerom den houck CGE, is even anden houck FGB. Maer den houck CGE ofte CGA is al een selfde, daerom den houck CGA, is even anden houck FGB.
Anghesien EG rechthouckich op DC, ghemeene sijde is der driehoucken DEG, ende CEG, oock dat DE even is an EC deur de I begheerte, so is DG even an CG {26.v.I.b.E.}, voort is den houck CGE even anden houck DGE {15.v.I.b.E.}; Maer den houck FGB, is oock even anden houc DGE, daerom den houck CGE, is even anden houck FGB. Maer den houck CGE ofte CGA is al een selfde, daerom den houck CGA, is even anden houck FGB.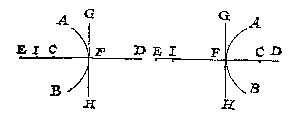

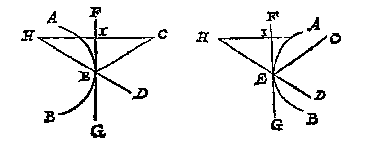

 Dit soo wesende ick segh H de begheerde schaeu te wesen.
Dit soo wesende ick segh H de begheerde schaeu te wesen. Neemt voor een bol clootspieghel als A, een brandende keers wiens vlam deur t'punt B beteeckent sy, in een camer sonder ander licht (tis wel waer datmen sulcx met eenich ander lichaem soude meughen doen voor een clootspieghel inden dach, maer wy hebben liever t'merckelickste voorbeelt te stellen) met de twee punten C, D, worden beyde d'ooghen beteeckent, welcke soo staen, dat D naerder de spieghel is dan C, inder voughen datmen sijn ooghen sal moeten keeren ende sijdeling naer de schaeuwen sien.
Neemt voor een bol clootspieghel als A, een brandende keers wiens vlam deur t'punt B beteeckent sy, in een camer sonder ander licht (tis wel waer datmen sulcx met eenich ander lichaem soude meughen doen voor een clootspieghel inden dach, maer wy hebben liever t'merckelickste voorbeelt te stellen) met de twee punten C, D, worden beyde d'ooghen beteeckent, welcke soo staen, dat D naerder de spieghel is dan C, inder voughen datmen sijn ooghen sal moeten keeren ende sijdeling naer de schaeuwen sien.