Home | Stevin | < Waterwicht >

10: Kracht op bodem , met iets drijvends , ander vlak , hydrostatische paradox
11: kracht tegen wand , vertikaal , schuin , ellips , getallenvoorbeeld

S . S T E V I N S     B E G H I N S E L E N   D E S   W A T E R W I C H T S.

[ 20 ]

V I I I   V E R T O O C H.           X   V O O R S T E L.

  O P  yder bodem des waters euewydich sijnde vanden sichteinder {Parallelum cum Horizonte.} , rust een ghewicht euen ande swaerheyt waters die euegroot is met den pilaer, wiens grondt dien bodem is, ende hoochde, de hanghende lini van t'plat {Perpendicularis.   Plano.}  duer t'waters oppervlack tot den grondt.

  T' G H E G H E V E N.   Laet ABCD een water sijn, van form een lichamelick rechthouck, diens oppervlack AB is, ende eenighen bodem daer in EF, euewydich vanden sichteinder; Laet oock GE de hanghende lini sijn van t'plat duer t'waters oppervlack totten grondt EF, ende den pilaer begrepen onder den bodem EF ende hoochde EG, sy GHFE.
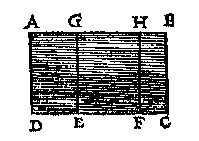bak water      T' B E G H E E R D E.   Wy moeten bewysen dat opden bodem EF, rust het ghewicht euen ande swaerheyt waters des pilaers GHFE.
  T' B E W Y S.   Soo op den bodem EF meer ghewicht rust dan des waters GHFE, dat sal moeten commen van weghen t'neuenstaende water; Laetet sijn soot mueghlick waer, van t'water AGED ende HBCF; Maer dat soo ghenomen, daer sal op den bodem DE, van weghen t'water GHFE, om dat de reden de selue is, oock meer ghewichts rusten dan des waters AGED; ende op den bodem FC, oock meer ghewichts dan des waters HBCF, ende veruolghens op den heelen bodem DC sal meer ghewichts rusten, dan des heelen waters ABCD, t'welck (ghemerckt ABCD een lichamelick rechthouck is) ongheschickt waer.
S'ghelijcx salmen oock bethoonen dat opden bodem EF niet min en rust dan t'water GHFE, daer rust dan nootsakelick op t'ghewicht euen ande swaerheyt waters des pilaers GHFE.

I   V E R V O L G H.

  Laet ons nu in t'water ABCD des 10en voorstels, legghen een styflichaem IKLM, stoflichter dan water, dat is driuende op t'water, mettet deel NOLM daer binnen, ende mettet deel NOKI daer buyten, welcker ghestalt dan sy als hier onder.


[ 21 ]
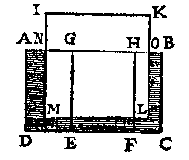bak water, drijvend blok Dit soo sijnde, t'stijflichaem IKLM is euewichtich metter water euegroot an NOLM duer het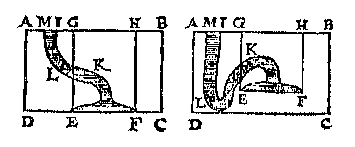 5e voorstel, waer duer t'lichaem IKLM, met de rest des waters rondom hem, euewichtich is an een lichaem waters euegroot an ABCD: daerom segghen wy noch naer luyt des voorstels, dat teghen den bodem EF een ghewicht rust, euen ande swaerheyt waters die euegroot is met den pilaer, diens grondt EF is, ende hoochde de hanghende lini GE, van t'plat {Plano.} AB, duer t'waters oppervlack AN totten grondt EF:
Waer uyt blijckt dat eenighe drijuende stof in t'water gheleyt, sy en verswaert noch en verlicht (welverstaende als t'water inde selfde hoochde blijft) den grondt niet.

I I.   V E R V O L G H.

  Laet andermael int water ABCD, legghen een styflichaem, ofte verscheyden styflichamen euestofswaer mettet water, ick neem alsoo, datter maer water en blijft als t'begrepen binnen IKFELM; T'welck so sijnde, dese lichamen en beswaren noch en verlichten den grondt EF niet meer dan t'water eerst en dede:

2 bakken, water in smalle vormen met zelfde brede bodem
Daerom segghen wy noch naer luyt des voorstels, dat teghen den bodem EF, een ghewicht rust euen ande swaerheydt waters die euegroot is metten pilaer, wiens grondt EF is, ende hoochde de hanghende lini GE, van t'plat AB duer t'waters oppervlack MI, totten grondt EF.

I I I   V E R V O L G H.

  Laet wederom ABCD t'eenemael water sijn, ende EF een bodem daer in euewydich vanden sichteinder. T'welck soo wesende, t'water onder den bodem EF, stoot euen soo stijf daer teghen opwaert, als t'water bouen den bodem EF, daer teghen neerwaert stoot:
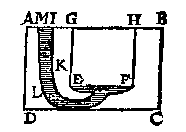bak, water in smalle vorm, nu van onder tegen zelfde bodem Want by aldient soo niet en waer, t'cranckste soude voor t'sterckste wycken, t'welck niet en ghebuert, want yder houdt sijn ghegheuen plaets duer het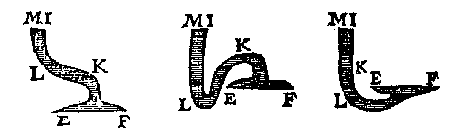 Ie voorstel. Laet nu eenighe styflichamen euestofswaer mettet water, alsoo gheleyt worden, dattet water IKEFLM, van onder anstoot teghen EF, als hier neuens. Dit soo sijnde, t'water onder den bodem EF, stoot nu so stijf teghen EF, dat is teghen t'stijflichaem, alst te vooren teghen t'water dede;

[ 22 ]
maer t'stac daer teghen soo stijf als t'bouenste teghen EF stiet, soo vooren gheseyt is, ende t'bouenste stiet teghen EF naer luydt deses voorstels, daerom t'onderste stoot oock teghen EF naer luydt deses voorstels, dat is soo wy bouen gheseyt hebben, dat teghen den bodem EF noch een ghewicht rust, euen ande swaerheyt waters die euegroot is metten pilaer, diens grondt EF is, ende hoochde de hanghende lini GE, van t'plat AB duer t'waters oppervlack MI totten grondt EF.

I I I I   V E R V O L G H.

  Laet ons nu de styflichamen des 2en ende 3en vervolghs tot haer plaets hechten, ende t'water uytghieten, ende daer sal een ledighe plaets IKFELM blijuen, ende den grondt EF en sal geen ghewicht draghen; waer uyt blijckt, dat met die cleyne ledighe plaets weder vol waters te ghieten, so salmen den grondt EF euen so seer beswaren, als of t'gheheele vat ABCD (de ingheleyde styflichamen gheweert sijnde) vol waters waer.

V   V E R V O L G H.

  Maer anghesien de ingheleyde styflichamen des 2en ende 3en veruolghs t'haerder plaets gehecht sijn, soo en gheeft noch en neemt haer uyterste stof tot de beswaring ofte verlichting des grondts EF, daerom laet ons de stof der seluer rondtom afcorten, alsoo datter blijuen de inwendighe ongheschickte formen ofte vaten met water ghevult MIKFEL, als hier onder.

3 vormen met water, zonder bak
  Ende sullen noch segghen naer luyt des voorstels, dat teghen den bodem EF een ghewicht rust, euen ande swaerheyt waters die euegroot is metten pilaer, wiens grondt EF is, ende hoochde de hanghende lini van t'plat duer t'waters oppervlack MI, totten grondt EF.   Ende dit alsoo om de selue reden van alle ander formen diens bodems in een plat sijn euewydich vanden sichteinder.
  T' B E S L V Y T.   Op yder bodem dan des waters euewydich sijnde, &c.

  Lees d'eruaringhen hier af breeder inden Anuang der Waterwichtdaet.

[ 23 ]
  M E R C K T.   Wy souden t'boveschreuen 10e voorstel eyghentlicker aldus uytghesproken hebben:

  O P  yder bodem des waters in een weereltvlack sijnde, rust een ghewicht euen ande swaerheyt waters die euegroot is mettet clootsdeel begrepen tusschen den bodem ende tweereltvlack duer t'waters hoochste punt, ende t'vlack tusschen die twee vlacken, beschreuen met de oneindelicke rechte lini vast in t'weerelts middelpunt, ende ghedraeyt duer des bodems omtreck.   {Circumferentiam.}

  Daer af bewysende sulcx als bouen bewesen is, maer om de redenen onder de 7e begheerte verclaert, soo ist beter ghelaten.


I X.   V E R T O O C H.           X I.   V O O R S T E L.

  W E S E N D E  een gheschickt bodem diens hoochste punt in t'waters oppervlack is: T'ghewicht daer teghen rustende is euen anden helft des pilaers waters, diens grondt euen an dien bodem is, ende hoochde, de hanghende lini {Perpendicularis.}  van des bodems hoochste punt, tot het plat {Plano.}  euewydich vanden sichteinder {Horizonte.}  duer des bodems leeghste punt.

Ie   V O O R B E E L T.

  T' G H E G H E V E N.   Laet AB een vat waters wesen, ende den bodem ACDE sy ten eersten een euewydich vierhouck, oneuewydich vanden sichteinder, daer op rechthouckich, diens hoochste sijde AC in t'waters oppervlack ACFG is, ende AE sy de hanghende lini van des bodems hoochste punt, tot het plat euewydich vanden sichteinder, ende duer des bodems leeghste punt, dat is duer ED, ende AG sy so lanck alst valt. Laet oock de lini DB euewydich sijn vanden sichteinder, ende daer in gheteeckent H, alsoo dat DH euen sy an DC, oock ghetrocken worden CH, ende met ACHDE sy beteeckent den helft des pilaers diens grondt ACDE, ende hoochde DH euen an AE.
  T' B E G H E E R D E.   Wy moeten bewysen dattet ghewicht waters teghen den bodem ACDE rustende, euen is anden voornoemden haluen pilaer ACHDE;

[ 24 ]   [ Figuur vereenvoudigd, zie 25 ]

bak, katrol
Dat is (om t'selue opentlicker te verclaren) ghenomen dat I een scheefwicht sy, eueswaer met ACHDE, diens trecklini KL, euewydich is met DH, ende dat K swaerheyts middelpunt sy vande macht des gheprangs vergaert inden bodem (wiens middelpunts vinding duer t'volghende 18e voorstel bekent wort) t'ghewicht I staet teghen t'gheprang des waters euewichtich, houdende den bodem ACDE (ghenomen datse beweeglick waer) in die standt.

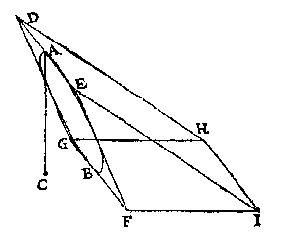
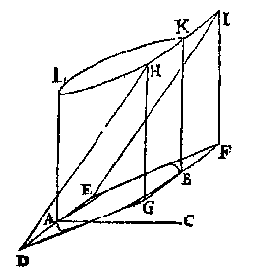
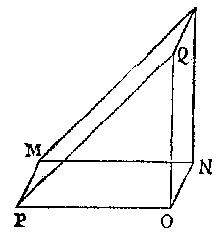driehoekig prisma   Ofte tot meerder claerheyt, laet MNOP een bodem sijn, euen ende ghelijck an ACDE, te weten de sijde MP lijckstandighe {Homologa.} met AC, ende MN met AE, op welcken bodem MNOP, light een stijflichaem MNOPQ, euen, ghelijck, ende eueswaer met den haluen pilaer ACHDE, ende de lini QO euen an DH, sy rechthouckich opden sichteinder.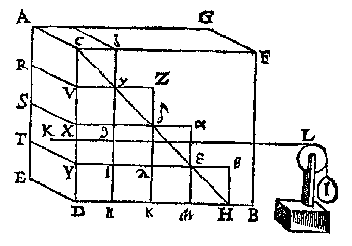
Ick seg dat alsulcken gheprang als dat stijflichaem MNOPQ, doet teghen den bodem MNOP, te weten meer pranghende naer NO dan naer MP, om dattet aldaer dicker en swaerder is dan alhier, euen soodanighen gheprang doet t'water AB, oock teghen den bodem ACDE, meer pranghende naer ED dan naer AC.

  T' B E R E Y T S E L.   Laet de sijde AE ghedeelt worden in vier euen deelen, met de punten R, S, T, ende daer uyt ghetrocken worden RV, SX, TY, euewydiche met AC; Laet oock ghetrocken worden VZ, Xalpha, Ybeta euewydighe met DH, ende sniende CH inde punten gamma, delta, epsilon, ende also, dat yder der linien gammaZ, deltaalfa, epsilonbeta, euen sy an Vgamma; Laet daernaer duer t'punt gamma ghetrocken worden de lini zetaeta, euewydighe met CD, sniende Xalfa in theta, ende Ybeta in iota, sghelijcx de lini Zkappa duer delta, sniende Ybeta in labda, sghelijcx de lini alfamu duer epsilon, ende ten laetsten betaH.

[ 25 ]   [ Figuur van blz 24 ]

blok, lijnen, katrol
  T' B E W Y S.   Teghen den bodem ACVR rust meer ghewichts dan niet, want waer dien bodem in t'waters oppervlack, soo souder niet teghen rusten, maer sy comt nu leegher, daer rust dan meer teghen als niet:
Ten anderen seg ick datter min teghen rust dan t'lichaem waters ACzetagammaVR, want waer sy euewydich vanden sichteinder duer RV, so souder dat lichaem ACzetagammaVR teghen rusten, duer het 10e voorstel, maer sy comt nu hoogher, daer rust dan min teghen.

S'ghelijcx seg ick dat teghen den bodem RVXS, meer ghewichts rust dan des lichaems ACzetagammaVR, want waer dien bodem euewydich vanden sichteinder duer RV, daer soude dat lichaem teghen rusten duer het 10e voorstel, maer sy comt nu leegher, daer rust dan meer teghen, maer t'lichaem RVgammathetaXS is euen an t'lichaem ACzetagammaVR, daerom teghen den bodem RVXS, rust meer ghewichts dan des lichaems RVgammathetaXS.
Ten anderen seg ick datter min teghen rust dan t'lichaem ACzetathetaXS, want waer dien bodem euewydich vanden sichteinder duer SX, soo souder dat lichaem ACzetathetaXS teghen rusten duer het 10e voorstel, maer sy comt nu hoogher, daer rust dan min teghen, maer t'lichaem RVZdeltaXS is euen an t'lichaem ACzetathetaXS, daerom rust teghen den bodem RVXS min als t'lichaem RVZdeltaXS.

S'ghelijcx seg ick dat teghen den bodem SXYT meer ghewichts rust dan des lichaems ACzetathetaXS, want waer dien bodem euewydich vanden sichteinder duer SX, daer soude dat lichaem teghen rusten duer het 10e voorstel, maer sy comt nu leegher, daer rust dan meer teghen, maer t'lichaem SXdeltalabdaYT is euen an t'lichaem ACzetathetaXS, daerom teghen den bodem SXYT rust meer ghewichts dan des lichaems SXdeltalabdaYT.
Ten anderen seg ick datter min teghen rust dan t'lichaem ACzetaiotaYT, want waer dien bodem euewydich vanden sichteinder duer TY, soo souder dat lichaem ACzetaiotaYT teghen rusten, duer het 10e voorstel, maer sy comt nu hoogher, daer rust dan min teghen, maer t'lichaem SXalfaepsilonYT is euen an t'lichaem ACzetaiotaYT, daerom rust teghen den bodem SXYT min als t'lichaem SXalfaepsilonYT.

S'ghelijcx seg ick dat teghen den bodem TYDE, meer ghewichts rust dan des lichaems ACzetaiotaYT, want waer dien bodem euewydich vanden sichteinder duer TY, daer soude dat lichaem teghen rusten duer het 10e voorstel, maer sy comt nu leegher, daer rust dan meer teghen, maer t'lichaem TYepsilonmuDE is euen an t'lichaem ACzetaiotaYT, daerom teghen den bodem TYDE rust meer ghewichts dan des lichaems TYepsilonmuDE.
Ten anderen seg ick datter min teghen rust dan t'lichaem ACzetaetaDE, want waer dien bodem euewydich vanden sichteinder duer ED, so souder dat lichaem ACzetaetaDE teghen rusten, duer het 10e voorstel, maer sy comt nu hoogher, daer rust dan min teghen, maer t'lichaem TYbetaHDE, is euen an t'lichaem ACzetaetaDE, daerom rust teghen den bodem TYDE min als t'lichaem TYbetaHDE.

[ 26 ]
Nu anghesien als vooren bewesen is, dat teghen den bodem ACVR meer rust dan niet, ende teghen den bodem RVXS m eer als t'lichaem RVgammathetaXS, ende teghen den bodem SXYT meer dan t'lichaem SXdeltalabdaYT, ende teghen den bodem TYDE meer als t'lichaem TYepsilonmuDE, soo rust teghen den heelen bodem ACDE meer dan t'ghewicht van alle die lichamen t'samen, t'welck is t'binneschreuen lichaem RVgammathetadeltalabdaepsilonmuDE inden haluen pilaer ACHDE:
Tis oock bewesen dat teghen den bodem ACVR min rust dan t'lichaem ACzetagammaVR, ende teghen den bodem RVXS min als tlichaem RVZdeltaXS, ende teghen den bodem SXYT min dan t'lichaem SXalfaepsilonYT, ende teghen den bodem TYDE min als t'lichaem TYbetaHDE, daerom rust teghen den heelen bodem ACDE min dan t'ghewicht van alle die lichamen t'samen, dat is t'omschreuen lichaem ACzetagammaZdeltaalfaepsilonbetaHDE.

Maer datmen nu den bodem ACDE welcke hier bouen ghedeelt is in vier euen deelen, alsoo deelde in acht euen deelen, tis kennelick dat het binneschreuen lichaem inden haluen pilaer ACHDE, ende het omschreuen, alsdan van dien haluen pilaer maer den helft soo veel verschillen en souden als sy nu doen, tis dan openbaer duer sulcke oneindelicke deeling des bodems, datter gheen ghewicht soo cleen ghegheuen en can worden, oft men sal bethoonen dattet verschil (sooder eenich waer) des ghewichts teghen den bodem ACDE rustende, tot het ghewicht des haluen pilaers ACHDE noch minder is, waer uyt ick aldus strije:
A.   Alle swaerheyt die min verschilt ven t'ghewicht teghen den bodem ACDE rustende dan ghegheuen can worden, is euen mettet ghewicht teghen den bodem ACDE rustende ;
I.   T'ghewicht des haluen pilaers ACHDE, is een swaerheyt die min verschilt van t'ghewicht teghen den bodem ACDE rustende dan ghegheuen can worden ;
I.   T'ghewicht dan des haluen pilaers ACHDE, is euen mettet ghewicht teghen den bodem ACDE rustende.


I Ie   V O O R B E E L T.

  T' G H E G H E V E N.   Laet AB andermael een vat waters wesen, ende den bodem ACDE sy een euewydich vierhouck des selfden, oneuewydich vanden sichteinder, ende daerop scheefhouckich, diens hoochste sijde AC in t'waters oppervlack ACFG is; T'selue water ende bodem sy alsoo ghedeelt ende gheteeckent als t'water des Ien voorbeelts, ende Anu sy hanghende lini van des bodems hoochste sijde, tot het plat euewydich vanden sichteinder duer des bodems leegste sijde ED.
  T' B E G H E E R D E.   Wy moeten bewysen dattet ghewicht waters teghen den bodem ACDE rustende, euen is anden helft des pilaers diens bodem ACDE, ende hoochde Anu.

[ 27 ]

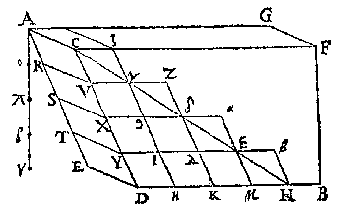
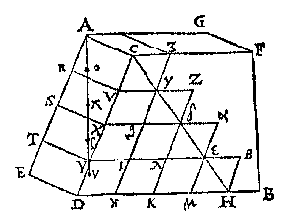
blok met schuine kant, lijnen
  T' B E R E Y T S E L.   Laet de sijde Anu ghedeelt worden in vier euen deelen, met de punten nu, pi, rho
  T' B E W Y S.   Teghen den bodem ACVR, rust meer ghewichts dan niet, want waer dien bodem in t'waters oppervlac, soo souder niet teghen rusten, maer sy comt nu leeger, daer rust dan meer teghen als niet:
Ten anderen seg ick datter min teghen rust dan den pilaer diens gront ACVR is, ende hoochde Ao, want waer sy euewydich vanden sichteinder duer RV, soo souder dien pilaer teghen rusten duer het 10e voorstel, maer sy comt nu hoogher, daer rust dan min teghen, maer ACzetagammaVR is euen an dien pilaer {31. v. II. B. E.}, daerom teghen den bodem ACVR rust min ghewicht dan des pilaers ACzetagammaVR.
blok met schuine kant, lijnen
S'ghelijcx salmen oock al de rest bethoonen euen soo sy in t'eerste voorbeelt bewesen was, waer uyt besloten sal worden dattet ghewicht teghen den bodem ACDE rustende, euen is an t'lichaem ACHDE, maer dat lichaem is euen anden helft des pilaers diens bodem ACDE, ende hoochde Anu, (want Anu is euen ande hanghende van H rechthouckich op t'plat duer ACDE)
Daerom t'ghewicht teghen den bodem ACDE rustende, is euen anden helft des pilaers waters diens grondt euen is an ACDE, ende hoochde Anu.


I I I.   V O O R B E E L T.

  T' G H E G H E V E N.   Laet AB eenich gheschickt bodem sijn; Ick neem een scheefrondt {Ellipsim.}, diens hoochste punt A in t'waters oppervlack is, ende B sy t'leeghste punt, ende AC de hanghende lini van t'hoochste punt A, tot het plat euewydich vanden sichteinder duer B.

[ 28 ]

ellips in schuin vlak
  T' B E G H E E R D E.   Wy moeten bewysen dattet ghewicht waters teghen den bodem AB rustende, euen is anden helft des pilaers diens grondt den bodem AB is, ende hoochde AC.
  T' B E R E Y T S E L.   Laet ghetrocken sijn een euewydich vierhouck DEFG, in wiens plat begrepen sy t'scheefrondt AB, alsoo dat DE in t'waters oppervlack sijnde, naecke an t'punt A, ende dat GF naecke an t'punt B; Laet daernaer ghetrocken worden FI euen an AF ende rechthouckich op FG maer euewydich vande sichteinder, ende uyt GF ende FI sy beschreuen den rechthouck FGHI, voorts de linien EI ende DH.
vorige gekanteld
  Laet daer naer een ander form ghestelt sijn euen, ghelijck, ende eueswaer met de voorgaende, maer alsoo dat FI rechthouckich sy opden sichteinder ghelijck hier neuen. Ende laet in dese tweede form t'lichaem DEFGHI een stijflichaem wesen, rustende opden bodem DEFG.

  T' B E W Y S.   Alsulcken drucksel als t'stijflichaem DEFGHI der tweeder form, veroirsaeckt teghen den bodem DEFG, euen soodanighen drucksel veroirsaeckt het water des eersten forms teghen sijn bodem DEFG, soo bouen bewesen is, ende veruolghens alsulcken drucksel alsser valt teghen t'scheefrondt AB der tweede form, euen soodanighen drucksel valter oock teghen t'scheefrondt AB der eerste form, maer het drucksel op t'scheefrondt der tweede form is den helft des pilaers (soo wy hier onder verclaren sullen) diens grondt dat scheefrondt is, ende hoochde euen an AC (want ghetrocken een hanghende lini van K rechthouckich op t'plat duer t'scheefrondt AB, sy is euen an AC)

[ 29 ]
daerom het drucksel des waters teghen t'scheefrondt AB der eerste form, is euen anden helft des pilaers wiens grondt dat scheefrondt is, ende hoochde AC.

  Maer dattet ghewicht rustende in dese tweede form teghen t'scheefrondt AB, euen is anden helft des pilaers diens grondt dat scheefrondt is, ende hoochde euen an AC, wort aldus bethoont: Laet ghetrocken worden de lini BK euen ende euewydighe met FI; Laet nu het onderste B der selue lini BK, ghedraeyt worden inden omtreck des scheefrondts AB, tot dat sy weder ter plaets comt daer sy begon te roeren, ende blijuende int roeren altijdt euewydich van FI, de selue sal tusschen de twee bodems een pilaer ABKL beschrijuen, welcke mettet plat DEIH, ghesneen wort duer twee lijckstandighe punten A, K, schuens teghen ouer malcander staende inde omtrecken der bodems;
Maer alle pilaer diens grondt een gheschickt bodem sijnde, ghesneen wort met een plat duer twee lijckstandighe punten inde omtrecken der bodems schuens teghen ouer malcander staende, die pilaer wort van dat plat in twee euen deelen ghedeelt, daerom het deel diens pilaers onder t'plat DEIH, is den helft des heelen pilaers ABKL rustende op t'scheefrondt AB, maer dat den pilaer ABKL euen is anden pilaer diens grondt AB ende hoochde AC, blijckt daer an, dat sijn hoochde euen is an AC, daerom t'ghewicht rustende teghen t'scheefrondt AB, is euen anden helft des pilaers diens grondt dat scheefrondt is, ende hoochde euen an AC.


I I I Ie   V O O R B E E L T.

  Wy heben hier bouen drie voorbeelden ghegheuen met Wisconstich bewys {Mathematica demonstratione.}, t'welck, wel is waer, den grondt volcommentlicker verclaert als ander; doch anghesien t'bewys duer ghetalen tot opentlicker kennis van alles niet en verachtert, sullen dit 4e voorbeelt duer ghetalen stellen.
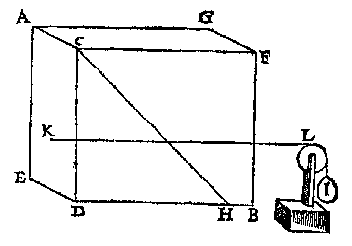
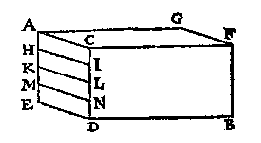bak water      T' G H E G H E V E N.   Laet AB een vat waters sijn, diens bodem [ACDE] wy nemen te wesen een rechthouckich vierhouck, rechthouckich opden sichteinder, ende d'hoochste sijde AC doende een voet, sy int waters oppervlack ACFG, ende AE doe oock een voet, maer AG sy soo lanck alst valt.
  T' B E G H E E R D E.   Wy moeten duer ghetalen bewysen, dattet ghewicht waters rustende teghen den bodem ACDE, euen is anden helft des pilaers waters, wiens grondt euen is an dien bodem, ende hoochde de hanghende lini AE: Maer dien pilaer is een teerlinck doende een voet, wy moeten dan bethoonen dat teghen den bodem ACDE rust het ghewicht van een halue voet waters.

[ 30 ]
  T' B E R E Y T S E L.   Laet duer den bodem ghetrocken worden drie euewydighe linien met AC als HI, KL, MN, alsoo dat AH euen sy an HK, ende an KM, ende an ME.
  T' B E W Y S.   Tis blijckelick dat op den bodem AI meer rust dan 0, want alwaer sulcken bodem duer AC euewydich vanden sichteinder, so souder 0 op rusten, maer sy comt nu leegher daer rust dan meer op als 0.   Ten anderen seg ick datter min op rust dan 1/16, voets, want al waer sulcken bodem duer HI euewydich vanden sichteinder, so souder 1/16 voets op rusten, maer sy comt nu hoogher, daer rust dan min op als 1/16, ende om der ghelijcke reden ist oock openbaer, dat op den bodem HL meer rust dan 1/16, ende min als 2/16, ende op den bodem KN meer dan 2/16, en min als 3/16; maer op den bodem MD meer dan 3/16 ende min als 4/16.
Nu dan vergaert de vier ghewichten (ghenomen dat 0 ghewicht waer) die lichter sijn d'ander op elken bodem rust, als 0. 1/16. 2/16. 3/16. maken t'samen 6/16:   Insghelijcx vergaert de vier ghewichten die swaerder sijn d'ander op elcken bodem rust, als 1/16. 2/16. 3/16. 4/16. maken t'samen 10/16:   Tis dan openbaer dat opden heelen bodem ACDE meer rust dan 6/16 voets, ende min als 10/16 voets, tusschen welke twee den 1/2 voet is, die wy noch bewysen moeten opden bodem ACDE te rusten.

  Nu ghelijck den bodem hier bouen duer de drie euewydighe linien ghedeelt is in vieren, also mueghen wyse deelen in soo veel deelen alst ons belieft, latet sijn in thienen, ende om de voorgaende redenen, de thien ghewichten die lichter sijn d'ander op elcken bodem rust, sullen sijn 0. 1/100. 2/100. 3/100. 4/100. 5/100. 6/100. 7/100. 8/100. 9/100. t'samen 45/100.   s'ghelijcx de thien ghewichten die swaerder sijn d'ander op elcken bodem rust, als 1/100. 2/100. 3/100. 4/100. 5/100. 6/100. 7/100. 8/100. 9/100. 10/100. maken t'samen 55/100;   tis dan kennelick dat opden bodem ACDE meer rust dan 45/100 voets, ende min als 55/100 voets, tusschen welke twee den haluen voet is die wy noch bewysen moeten opden bodem ACDE te rusten:   Maer dese twee palen {Termini.} sijn naerder den haluen voet dan d'eerste twee, want min verschilt 45/100 van 1/2, dan 6/16, alsoo oock verschilt 55/100 min van 1/2, dan 10/16;   Waer uyt blijckt dat hoe wy den bodem ACDE in meer sulcke euen deelen snien, hoe dat wy den haluen voet altijdt naerder commen.

  T'welck so verstaen sijnde, laet opden bodem ACDE min of meer rusten 1/1000 voets (waert mueghelick) dan een halue voet, ende laet ons de waerheyt daeraf ondersoucken, deelende den bodem duer de ghedacht in 1000 euen deelen alsvooren. Ende om de voorgaende redenen, de duysent ghewichten die lichter sijn dander op elcken bodem rust, sullen sijn 0, 1/1000000. 2/1000000 ende so voorts tot het laetste, dat sijn sal van 999/1000000, alle welcke ghetalen t'samen, sullen maken (wiens corte manier om te vergaren wy hier onder verhalen sullen) 499500/1000000.


[ 31 ]   [ breuken hier met schuine streep ]
Sghelijcx de duysent ghewichten die swaerder sijn d'ander op elcken bodem rust als 1/1000000. 2/1000000. 3/1000000. ende so voorts tot het laetste, dat sijn sal van 1000/1000000, maken t'samen 500500/1000000, daer rust dan meer opden bodem als 499500/1000000 voets, ende min dan 500500/1000000 voets;   Maer 499500/1000000 en is maer 1/2000 minder dan 1/2, daer en rust dan gheen 1/1000 voets min opden bodem dan 1/2 voet. Alsoo en is 500500/1000000 maer 1/2000 meerder dan 1/2. daer en rust dan gheen 1/1000 meer op den bodem dan 1/2 voet.
Ende alsoo salmen dierghelijcke bethoonen ouer alle ghestelt deel hoe cleen het sy. Het blijckt dan, dat het verschil (sooder eenich waer) tusschen t'water opden bodem ACDE rustende, ende een halue voet waters, minder soude moeten sijn dan mueghelick is ghestelt te worden, waer uyt ick aldus strije:
A.   Neuen yder ghewicht dat met een halue voet waters verschil heeft, can een ghewicht ghestelt worden daer af min verschillende ;
O.   Neuen t'ghewicht waters opden bodem ACDE rustende, en can gheen ghewicht ghestelt worden van een halue voet waters min verschillende  ;
O.   T'ghewicht waters dan opden bodem ACDE rustende, een heeft met een halue voet waters gheen verschil.

  T' B E S L V Y T.   Wesende dan een gheschict bodem diens hoochste punt int waters, &c.


D E reden waerom het half hier bouen, altijt blijft tusschen de twee ghetalen, welcke an het half oneindelick naerderen, maer nummermeer daer toe en gheraken, is begrepen in sulcken vertooch {Theoremate.}:

  W E S E N D E  een voortganck van ghetalen malcanderen in eenheydt te bouen gaende, ende beghinnende van de eenheyt: Den helft des viercants van t'laetste, is meerder [minder] dan de somme van al de ghetalen, maer minder [meerder] dan de somme van al de ghetalen min t'laetste.

M A E R  om te verclaren (als bouen belooft is) de manier om duer cortheyt te vergaren die groote menichte der ghetalen; Soo is ten eersten kennelick, dat haer noemers al euen sijn, waerduer wy alleenelick op der ghetalen telders te letten hebben, de selue sijn in oirdentlicke voorganck {Progressione.} beghinnende vande eenheyt {Vnitate.}, ende met eenheyt malcanderen te bouengaende, daerom vermenichvuldicht t'laetste met sijn helft, ende an t'uytbreng noch ghevoucht sijn helft, gheeft de begheerde somme. By voorbeelt ick wil weten hoe veel de somme is van 1, 2, 3, 4, 5, 6; Ick seg 6 mael 3 is 18, met 3 maeckt 21 voor de begheerde somme.


[ 32 ]
Laet het laetste nu oneuen ghetal sijn, als 1, 2, 3, 4, 5, 6, 7; Ick seg 7 mael 3 1/2 is 24 1/2, met 3 1/2 maeckt 28, voor de begheerde somme. Maer als t'laetste aldus oneuen is, soo vallet lichter om duer gheen ghebroken te wercken, datmen t'laetste menichvuldicht duer den helft der somme van t'laetste met 1, als andermael willende weten de somme van 1, 2, 3, 4, 5, 6, 7; Ick doe 1 tot 7, maeckt 8, sijn helft is 4, die vermenichuuldicht duer 7, comt alsbouen 28, voor de begheerde somme, ende alsoo met allen anderen.

M E R C K T.

  Anghesien de boueschreuen helft des pilaers euen is anden heelen pilaer diens grondt den ghegheuen boden [bodem] is, ende hoochde den helft der hanghende lini van des bodems hoochste punt, tottet plat euewydich vanden sichteinder duer des bodems leeghste punt, men soude t'boueschreuen 11e voorstel oock mueghen aldus uyten:

  W E S E N D E  een gheschickt bodem diens hoochste punt in t'waters oppervlack is: T'ghewicht daer tegheu rustende is euen anden pilaer waters diens grondt euen an dien bodem is, ende hoochde den helft der hanghende lini van des bodems hoochste punt, tottet plat euewydich vanden sichteinder duer des bodems leeghste punt.

  Ende na sulcke wyse sullen wy t'laetste deel deses 12en voorstels formen.


X.   V E R T O O C H.       X I I.   V O O R S T E L.

  W E S E N D E een gheschickt bodem diens hoochste punt onder t'waters oppervlack is: T'ghewicht daer teghen rustende [ ... ].



Home | Simon Stevin | Waterwicht | Voorstel 10, 11 (top) | 12 - 16