A N V A N G D E R
W A T E R W I C H T D A E T,
B E S C H R E V E N D V E R
S I M O N S T E V I N
van Brugghe.
A N D E N L E S E R.
Anden Leser , 1: schip , 2: hydrostatische paradox , 3: mens diep onder water
[ 55 ]
A N D E N L E S E R.
 A D I E N hier vooren beschreuen sijn de Beghinselen des Waterwichts, soo soudet betamelick sijn, dat beken ick, de Waterwichtdaet te volghen, van sulcx als wy daer af connen verclaren; maer hebben om seker redenen gheschict, dat voor t'eerste niet schriftelick, maer werckelick te laten gheschien: Alleenlick sullen hier drie voorstellen setten, die opentlick uyt het voorgaende volghen, welcke ons niet weerdich dunckende den naem van Waterwichtdaet te verstrecken, doch ghemeenschap daer mede hebbende, wy noemense Anuang van dien. De selue beminde Leser belieue v int goede te nemen, ende de rest t'sijnder tijdt te verwachten. A D I E N hier vooren beschreuen sijn de Beghinselen des Waterwichts, soo soudet betamelick sijn, dat beken ick, de Waterwichtdaet te volghen, van sulcx als wy daer af connen verclaren; maer hebben om seker redenen gheschict, dat voor t'eerste niet schriftelick, maer werckelick te laten gheschien: Alleenlick sullen hier drie voorstellen setten, die opentlick uyt het voorgaende volghen, welcke ons niet weerdich dunckende den naem van Waterwichtdaet te verstrecken, doch ghemeenschap daer mede hebbende, wy noemense Anuang van dien. De selue beminde Leser belieue v int goede te nemen, ende de rest t'sijnder tijdt te verwachten.
|
|
T E vinden hoe veel een selfde lichaem dat stoflichter is als water, in t'een water dieper sijncken sal als int ander dat stofswaerder is. L A E T by voorbeelt een schip ligghen inden Rhijn te Leyen, ende men wil weten hoe veel dattet daerin dieper sincken sal dan in See voor Catwyck. Men sal ondersoucken de reden der stofswaerheyt van dat water tot dit, welcke sy als van 42 tot 43, soo heb ickse in Hoymaent duer d'eruaring beuonden, want nemende twee euegroote lichamen, dat vanden Rhijn wouch 4260 azen maer t'Seewater 4362 azen, t'welck na ghenouch is als van 42 tot 43. Daerom salmen segghen, de grootheyt des deels van dat schip onder water in den Rhijn is tot de grootheyt van sulck deel onder water in See voor Catwyck, als van 43 tot 42, waer uyt den Meter {Geometra.} naer gheleghentheyt der form des voorghestelden schips, dese diepte tot die sal connen oirdeelen, waer af de nootsaecklicheyt Wisconstlick {Mathematicè.} blijct int 7e voorstel der beghinselen des Waterwichts. D V E R daetlicke voorbeelden te verclaren het 10e voorstel der beghinselen des Waterwichts. W Y hebben int 10e voorstel der beghinselen des Waterwichts, int 5e vervolgh Wisconstlick bewesen, dat den bodem des waters aldaer EF, duer een grooter water (d'hoochde de selfde blijuende) niet meer beswaert en wort dan duer een cleinder, ende weder verkeert, datse duer een cleinder water soo seer beswaert wort, als duer een grooter: Maer want den menighen dat voor onnatuerlick mocht achten, sullen bouen t'voorgaende Wisconstich bewys, daeraf vijf daetlicke voorbeelden beschrijuen, welcke yghelijck versoucken, ende ooghenschijnlick sien mach. |
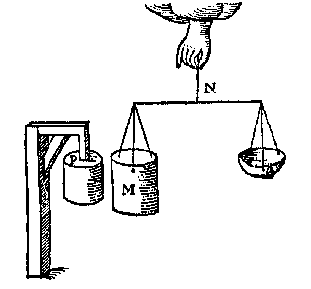
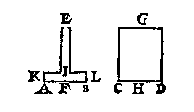 L A E T den bodem AB euen ende ghelijck sijn anden bodem CD, ende de hoochde des waters op AB als EF, sy euen ande hoochde des waters op CD, als GH; maer het deel IE bouen t'water KLBA staende, sy cleender dan alsulck deel des lichaems GCD, ende t'water van EAB weghe 1 lb, ende van GCD 10 lb, ende de form van GCD sy een rondt pilaer, ende t'water GCD sal thienmael grooter en swaerder sijn dan t'water EAB, nochtans segghen wy t'ghewicht des waters EAB, euen soo stijf te drucken opden grondt AB, als t'ghewicht des waters GCD opden bodem CD.
L A E T den bodem AB euen ende ghelijck sijn anden bodem CD, ende de hoochde des waters op AB als EF, sy euen ande hoochde des waters op CD, als GH; maer het deel IE bouen t'water KLBA staende, sy cleender dan alsulck deel des lichaems GCD, ende t'water van EAB weghe 1 lb, ende van GCD 10 lb, ende de form van GCD sy een rondt pilaer, ende t'water GCD sal thienmael grooter en swaerder sijn dan t'water EAB, nochtans segghen wy t'ghewicht des waters EAB, euen soo stijf te drucken opden grondt AB, als t'ghewicht des waters GCD opden bodem CD. T'welck aldus daetlick bewesen wort: |
|
Laet MNO een waegh sijn, diens schalen M, O, welcker schalen M vande form eens pilaers sy, euen ende ghelijck an t'vat hier bouen GCD, ende sal houden 10 lb waters; Laet oock P een houten lichaem wesen, vast staende als hier neuen, ende lijckformich ande schael M, maer soo veel cleender datment daerin steken can sonder erghens ande schael te ghenaken.
Laet nu t'lichaem P ghesteken worden inde schael M, als in dees tweede form, ende inde schael O sy gheleyt t'ghewicht Q van 10 lb, ende den bodem der schael M sal soo stijf ghenaken teghen t'onderste des lichaems P, als de 10 lb van Q veroirsaken. |
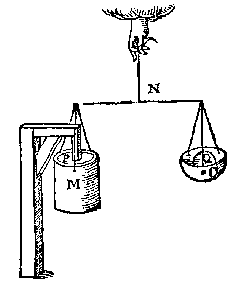 Dit soo sijnde daer is water tusschen den bodem der schael M ende t'onderste des lichaems P, teghen welck water den bodem van M nu soo stijf druck, als sy eerst teghen t'onderste des lichaems P stack, want t'selue ghewicht Q ligt noch in d'ander schael O; Maer sy stack eerst soo stijf daer teghen als 10 lb van Q veroirsaeckten, daerom den bodem van M steeckt soo stijf teghen t'water als de 10 lb van Q veroirsaken, ende, weder verkeert, t'water steeckt soo stijf teghen den bodem M, als die 10 lb van Q veroirsaecken.
Dit soo sijnde daer is water tusschen den bodem der schael M ende t'onderste des lichaems P, teghen welck water den bodem van M nu soo stijf druck, als sy eerst teghen t'onderste des lichaems P stack, want t'selue ghewicht Q ligt noch in d'ander schael O; Maer sy stack eerst soo stijf daer teghen als 10 lb van Q veroirsaeckten, daerom den bodem van M steeckt soo stijf teghen t'water als de 10 lb van Q veroirsaken, ende, weder verkeert, t'water steeckt soo stijf teghen den bodem M, als die 10 lb van Q veroirsaecken.Laet ons nu nemen dattet water opden bodem M ligghende, euegroot sy an t'water KLBA, ende de rest rondtom t'licham P staende, euegroot mettet water IE; t'water dan EAB, druckt euen soo stijf teghen den grondt AB, als dit water teghen den grondt M, maer dit druckt soo stijf als 10 lb, soo bouen bethoont is, dat water EAB dan, druckt oock soo stijf teghen den grondt AB als 10 lb, ende so stijf druck oock t'water GCD teghen den grondt CD: Daerom soo wy voorghenomen hadden daetlick te bewysen, t'water EAB weghende 1 lb, druckt euen soo stijf teghen sijn grondt AB, als t'water GCD weghende 10 lb, teghen sijn grondt CD. Ende ghelijck wy hier bewysen 1 lb so stijf te drucken als 10 lb, alsoo salmen oock bewysen 1 lb stijuer te connen drucken als duysent ponden. 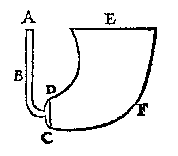 Laet ABCD een cleen dun buysken sijn, ende CDEF een groot dick vat afghesondert van t'buysken, met een ghemeene bodem CD, ende beyde vol waters, alsoo dat der wateren oppervlacken in een selfde weereltvlack sijn. Nu dat het groot water des vats CDEF, niet stijuer en druckt teghen den bodem CD, dan t'cleyne water der cleyne buys, blijckt daetlick aldus:
Laet ABCD een cleen dun buysken sijn, ende CDEF een groot dick vat afghesondert van t'buysken, met een ghemeene bodem CD, ende beyde vol waters, alsoo dat der wateren oppervlacken in een selfde weereltvlack sijn. Nu dat het groot water des vats CDEF, niet stijuer en druckt teghen den bodem CD, dan t'cleyne water der cleyne buys, blijckt daetlick aldus: Laet gheweert worden den bodem DC, ende t'groot water sal op die plaets teghen t'cleynste stooten: Nu soo t'water CDEF, van te vooren stijuer ghestooten had teghen den bodem DC, dan t'water ABCD, soo salt nu oock stijuer stooten teghen dat water dan dat teghen dit: |
|
waer duer t'cranckste voor t'sterckste sal moeten wycken, dat is, t'water ABCD sal rijsen, ende van CDEF sal dalen; Maer dit so wesende, haer oppervlacken en sullen niet euen hooch sijn t'welck opentlick teghen d'eruaring is. Daerom t'cleinste water ABCD druckt euen soo stijf teghen den bodem CD, als t'grootste water CDEF. Laet ABCD een vat vol waters sijn, in wiens bodem DC euewydich ligghende vanden sichteinder, een rondt gat EF is waer op ligt een ronde houten schijf GH, stoflichter dan water, ende dat gat EF bedeckende, ende rondtom dicht sluytende teghen den bodem DC. Laet oock IKL een ander vat vol waters sijn, euenhooch mettet vat ABCD, maer cleinder, in wiens bodem KL oock een rondt gat MN sy, euen an t'gat EF, waer op light een schijf OP, euegroot ende eueswaer ande schijf GH: 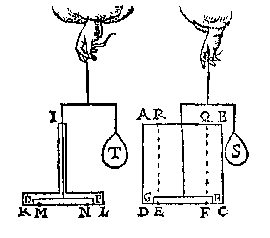 T'welck soo wesende, d'eruaring sal bethoonen dat de schijf GH niet rijsen en sal, naer de ghemeenen aert des hauts in t'water, maer sal so stijf op t'gat EF drucken, als een ghewicht eueswaer an t'water dat euegroot is anden pilaer EFQR, min t'verschil des ghewichts der houte schijf GH, tot het ghewicht des waters an die schijf euegroot.
T'welck soo wesende, d'eruaring sal bethoonen dat de schijf GH niet rijsen en sal, naer de ghemeenen aert des hauts in t'water, maer sal so stijf op t'gat EF drucken, als een ghewicht eueswaer an t'water dat euegroot is anden pilaer EFQR, min t'verschil des ghewichts der houte schijf GH, tot het ghewicht des waters an die schijf euegroot.Maer om sulcx duer de daet oock te sien, men mach ande schijf GH een waegh voughen, diens ghewicht S eueswaer sy an dat voornomde ghewicht, ende de schijf GH sal daer teghen euewichtich blijuen. Laet nu insghelijcx ande schijf OP oock een waegh voughen, diens ghewicht T eueswaer sy an S, ende de schijf OP sal daer teghen oock euewichtich blijuen. Maer soomen S ende T yet swaerder maeckt, sy sullen haer schijuen doen rijsen, inder voughen dat de schijuen GH, OP, duer sulcke euewichten beuonden worden euestijf teghen haer bodems te drucken, waer uyt het voornemen blijckt, te weten het cleinder water IKL, euen so stijf teghen sijn grondt te drucken, als t'grooter ABCD. |
|
Tis kennelick dat so t'verschil des ghewichts der schijf als GH, tot het ghewicht des waters an haer euegroot, meerder waer dan t'ghewicht des waters euegroot anden pilaer, als EFQR, sulcken schijf en soude op t'gat als EF niet connen rusten, maer soude nootsakelick oprijsen. T'is oock blijckelick dat soo de schijf al GH stofswaerder waer dan water, als van loot, yser, &c. datse dan op t'gat EF soo stijf drucken soude, als een ghewicht des waters euegroot anden pilaer EFQR, meer t'verschil des ghewichts der schijf, tottet ghewicht des waters an haer euegroot. Maer waer de schijf GH euestofswaer an t'water, tis openbaer datse dan effen so stijf op t'gat EF drucken soude, als een ghewicht des waters euegroot anden pilaer EFQR. 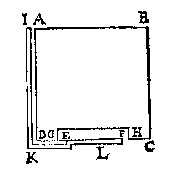 Laet ABCD een vat vol waters sijn, met een gat EF inden grondt CD, daerop een schijf GH light, stoflichter dan t'water, de selue sal op t'gat EF so stijf pranghen als vooren bewesen is.
Laet oock, IKL een cleen dun buysken wesen, diens opperste gat I inde selfde hoochde van AB sy, ende t'onderste gat sy EF: Daer naer dit buysken vol waters ghegoten, dat cleen water sal soo groot ghewelt doen teghen den grondt des schijfs GH, als al t'water dat in t'vat ABCD is, want de schijf GH sal rijsen. Inder voughen dat 1 lb waters (duer t'welck ick neem de buys IKL te mueghen ghevult worden) meer ghewelts sal connen doen teghen de schijf GH, dan hondert duysent ponden als S hier vooren, t'welckmen der naturen verborghenheyt soude mueghen noemen dat d'oirsaken onbekent waren.
Laet ABCD een vat vol waters sijn, met een gat EF inden grondt CD, daerop een schijf GH light, stoflichter dan t'water, de selue sal op t'gat EF so stijf pranghen als vooren bewesen is.
Laet oock, IKL een cleen dun buysken wesen, diens opperste gat I inde selfde hoochde van AB sy, ende t'onderste gat sy EF: Daer naer dit buysken vol waters ghegoten, dat cleen water sal soo groot ghewelt doen teghen den grondt des schijfs GH, als al t'water dat in t'vat ABCD is, want de schijf GH sal rijsen. Inder voughen dat 1 lb waters (duer t'welck ick neem de buys IKL te mueghen ghevult worden) meer ghewelts sal connen doen teghen de schijf GH, dan hondert duysent ponden als S hier vooren, t'welckmen der naturen verborghenheyt soude mueghen noemen dat d'oirsaken onbekent waren.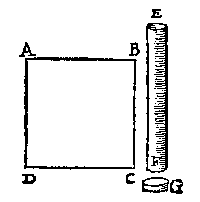 Om nu oock werckelick betooch te gheuen ouer de voorbeelden alwaer t'water opwaert teghen den bodem steeckt, als int 3e veruolgh des voornomden 10en voorstels, so laet ABCD een water sijn, ende EF een dichte buys, ende G een schijf stofswaerder dan water, ick neem van loot, als in dese eerste form.
Om nu oock werckelick betooch te gheuen ouer de voorbeelden alwaer t'water opwaert teghen den bodem steeckt, als int 3e veruolgh des voornomden 10en voorstels, so laet ABCD een water sijn, ende EF een dichte buys, ende G een schijf stofswaerder dan water, ick neem van loot, als in dese eerste form.Laet dese schijf G gheleyt worden teghen t'gat F, alsoo datse dicht daer op pas, ende de buys met de schijf dan alsoo t'samen in t'water ABCD ghesteken, ick neem tot H toe, als hier onder, |
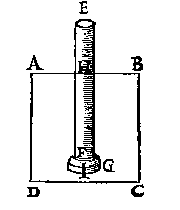 de schijf G en sal naer den ghemeenen aert des loots, in t'water niet sincken, maer ande buys blijuen hanghen, ende daer teghen soo stijf drucken, als een ghewicht eueswaer an t'water dat euegroot is anden pilaer, diens grondt de groote des gats F, ende hoochde HI is, min t'verschil des ghewichts der schijf G, tot t'ghewicht des waters an die schijf euegroot.
de schijf G en sal naer den ghemeenen aert des loots, in t'water niet sincken, maer ande buys blijuen hanghen, ende daer teghen soo stijf drucken, als een ghewicht eueswaer an t'water dat euegroot is anden pilaer, diens grondt de groote des gats F, ende hoochde HI is, min t'verschil des ghewichts der schijf G, tot t'ghewicht des waters an die schijf euegroot. Maer soo de schijf G niet dicht ghenouch teghen de buys en slote, ende datter eenich water indrong, soo sal de schijf G daer soo langhe anhanghen, tot dat sulck inghedronghen water t'voornomde ghewicht ouerwint. 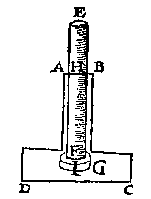 Maer want nu yemandt dencken mocht, het groot swaer water rondom de buys staende, stijuer drucking der schijf teghen de buys te veroirsaken, dan een cleender water van de selfde hoochde, soo laet ons t'water neuen de buys rondom afcorten, dat is, dat de reste water sy in een vat van form als hier neuen, ende d'eruaring sal bewysen (versouckende de macht des gheprangs in t'een en t'ander water, duer euewichten inde buys op G rustende) dit cleen water euen soo stijf te drucken als t'voornomde grooter, waer af de reden bouen grondelick beschreuen is.
Maer want nu yemandt dencken mocht, het groot swaer water rondom de buys staende, stijuer drucking der schijf teghen de buys te veroirsaken, dan een cleender water van de selfde hoochde, soo laet ons t'water neuen de buys rondom afcorten, dat is, dat de reste water sy in een vat van form als hier neuen, ende d'eruaring sal bewysen (versouckende de macht des gheprangs in t'een en t'ander water, duer euewichten inde buys op G rustende) dit cleen water euen soo stijf te drucken als t'voornomde grooter, waer af de reden bouen grondelick beschreuen is.T' B E S L V Y T. Wy hebben dan duer daetlicke voorbeelden het 10e voorstel der beghinselen des Waterwichts verclaert, naer t'voornemen. Wat het 11e voorstel belangt, daer uyt is onder anderen kennelick, wat ghewicht waters datter druct, teghen elcke siide der duer van een sluys, ende dierghelijcke: Oock dattet water ouer d'een siide alleenlick een stroobreet, daer teghen soo stijf prangt als t'water diens breede de Zee van Oceane ouer d'ander siide; Welverstaende als sy euenhooghe siin. Van welcke dinghen wy om haer voornoemde claerheyt hier gheen besonder voorstellen en maken |
|
D' O I R S A E C K te verclaren waerom een mensch diep onder t'water swemmende, niet doot gheprangt en wort, van t'groot ghewicht des waters op hem ligghende. Laet een mensch 20 voeten diep onder water ligghen, weghende elcke voet waters 65 lb, ende t'gheheel vlack sijns lichaems sy groot 10 voeten. Dit soo wesende, daer sal teghen sijn lijf perssen byde 13000 ponden ghewichts, duer het 10e ofte 11e voorstel vande beghinselen des Waterwichts. T'welck soo sijnde, hoe ist mueghelick, sal ymant segghen, dat sulcken ghewicht den mensch niet doot en druct? D'antwoort is daerop soodanich:
Des bewysredens tweede voorstel {Syllogismi minor.} is openbaer duer de daet, waer af de reden dese is: Soo eenich deel als vleesch, bloet, vochticheyt, wattet sy, uyt sijn natuerlicke plaets verset wierde, t'soude moeten plaets hebben daert in ghinge, die plaets en is buyten t'lichaem niet, ouermidts t'water oueral euestijf anstoot (Angaende t'onderste deel een weynich stijuer gheprangt wort dan t'opperste, duer het 11e voorstel der Beghinselen des Waterwichts, dat en is in desen gheualle van gheender acht, want sulck verschil gheen deel uyt sijn natuerlicke plaets versetten en can) sy en is oock binnen t'lichaem niet, wanttet daer soo vol lichamelickheyts is als daer buyten, waer duer yder dit deel, soo stijf stoot teghen yder dat deel, als yder dat, teghen yder dit, ouermits t'water rondom t'lichaem tot allen sijden met een selue reden staat. Die plaets dan en is buyten t'lichaem niet, noch daer binnen, daerom nerghens, waerduer het onmueghelick is, dat eenich deel uyt sijn natuerlicke plaets ghebrocht worde, ende vervolghens t'lichaem en can daeraf gheen weedom ontfaen. Maer om t'selue metter daet noch merckelicker te bewysen, laet ABCD een water sijn, hebbende inden grondt DC een gat, ghesloten met den tap E, ende opden seluen grondt ligghe een man F, met sijn rug op E: T'welck soo sijnde, daer en can van weghen t'ghewicht des waters op hem ligghende, gheen deel des lichaems uyt sijn natuerlicke plaets verset worden, ouermits t'water an allen sijden euestijf anstoot, als vooren gheseyt is. |
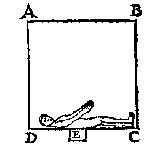 Maer wildi nu daetlick sien dit de waerachtighe oirsaeck te wesen, so trect den tap E uyt, ende dan en sal teghen sijn rug an E gheen stootsel sijn, als an alle d'ander plaetsen sijns lichaems, daerom oock sal het lichaem daer prangsel lijden, ende dat soo stijf als int derde voorbeelt des 2en voorstels van desen betoocht is; te weten soo stijf, als veroirsaeckt wort duer t'ghewicht des pilaers waters, diens gront het gat E is, ende hoochde, de hoochde des waters bouen hem, waermede t'voornemen opentlick bewesen is.
Maer wildi nu daetlick sien dit de waerachtighe oirsaeck te wesen, so trect den tap E uyt, ende dan en sal teghen sijn rug an E gheen stootsel sijn, als an alle d'ander plaetsen sijns lichaems, daerom oock sal het lichaem daer prangsel lijden, ende dat soo stijf als int derde voorbeelt des 2en voorstels van desen betoocht is; te weten soo stijf, als veroirsaeckt wort duer t'ghewicht des pilaers waters, diens gront het gat E is, ende hoochde, de hoochde des waters bouen hem, waermede t'voornemen opentlick bewesen is.
|