W E S E N D E den bodem des waters een euewydich vierhouck oneuewydich vanden sichteinder {Horizonte.}, met sijn bekende hoochste sijde in t'waters oppervlack, ende bekent sijnde t'ghewicht daer teghen rustende, oock de hanghende lini {Perpendicularis.} vande hoochste sijde tot het plat {Planum.} euewydich vanden sichteinder duer de leeghste sijde: De lini vande hoochste sijde rechthouckich op de voortghetrocken leeghste sijde bekent te maken.
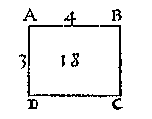 T' G H E G H E V E N. Laet ABCD een rechthouck wesen, rechthouckich opden sichteinder, daer teghen rustende t'ghewicht van 18 voeten waters, ende d'hoochste sijde AB in t'waters oppervlack sijnde, doet 4 voeten.
T' G H E G H E V E N. Laet ABCD een rechthouck wesen, rechthouckich opden sichteinder, daer teghen rustende t'ghewicht van 18 voeten waters, ende d'hoochste sijde AB in t'waters oppervlack sijnde, doet 4 voeten.T' B E G H E E R D E. Wy moeten de sijde AD bekent maken.
T' W E R C K. Ick deel de 18 duer 2, helft van AB, comt 9, diens viercantighe sijde voor AD doet 3 voeten.
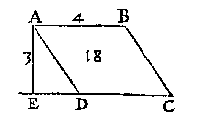 T' G H E G H E V E N. Laet ABCD een euewydich scheefhouckich vierhouck wesen, rechthouckich opden sichteinder, daer teghen rustende t'ghewicht van 18 voeten waters, ende d'hoochste sijde AB in t'waters oppervlack sijnde doet vier voeten.
T' G H E G H E V E N. Laet ABCD een euewydich scheefhouckich vierhouck wesen, rechthouckich opden sichteinder, daer teghen rustende t'ghewicht van 18 voeten waters, ende d'hoochste sijde AB in t'waters oppervlack sijnde doet vier voeten.T' B E G H E E R D E. Wy moeten de lini AE bekent maken.
T' W E R C K. Ick deel de 18 duer 2 helft van AB, comt 9, diens viercantighe sijde voor AE is 3 voeten.
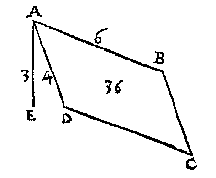 T' G H E G H E V E N. Laet ABCD een rechthouck wesen, scheefhouckich opden sichteinder, daer teghen rustende t'ghewicht van 36 voeten waters, ende de hoochste sijde AB in t'waters oppervlack sijnde doet 6 voeten, ende AE doende 3 voeten, sy de hanghende lini vande hoochste sijde tot het plat euewydich vanden sichteinder duer de leeghste sijde.
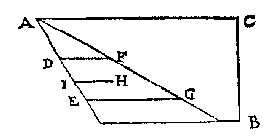
T' G H E G H E V E N. Laet ABCD een rechthouck wesen, scheefhouckich opden sichteinder, daer teghen rustende t'ghewicht van 36 voeten waters, ende de hoochste sijde AB in t'waters oppervlack sijnde doet 6 voeten, ende AE doende 3 voeten, sy de hanghende lini vande hoochste sijde tot het plat euewydich vanden sichteinder duer de leeghste sijde.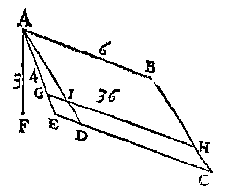 T' G H E G H E V E N. Laet ABCD een euewydich scheefhouckich vierhouck sijn scheefhouckich opden sichteinder, daerop rustende t'ghewicht van 36 voeten waters, ende de hoochste sijde AB in t'waters oppervlack sijnde, doet 6 voeten, ende AE sy de lini van d'hoochste sijde rechthouckich opde voortghetrocken leeghste sijde, ende AF doende 3 voeten, is de hanghende vande hoochste sijde tot het plat euewydich vanden sichteinder duer de leeghste sijde.
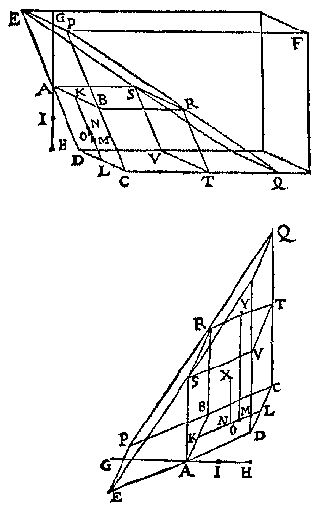
T' G H E G H E V E N. Laet ABCD een euewydich scheefhouckich vierhouck sijn scheefhouckich opden sichteinder, daerop rustende t'ghewicht van 36 voeten waters, ende de hoochste sijde AB in t'waters oppervlack sijnde, doet 6 voeten, ende AE sy de lini van d'hoochste sijde rechthouckich opde voortghetrocken leeghste sijde, ende AF doende 3 voeten, is de hanghende vande hoochste sijde tot het plat euewydich vanden sichteinder duer de leeghste sijde.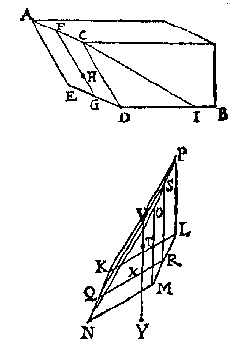 T' B E G H E E R D E. Wy moeten bewysen dat H t'swaerheyts middelpunt is des gheprangs inden bodem vergaert.
T' B E G H E E R D E. Wy moeten bewysen dat H t'swaerheyts middelpunt is des gheprangs inden bodem vergaert.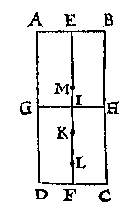 Laet ABCD een bodem sijn, daer in ghetrocken is de lini EF, tusschen de middelen van AB, ende DC, deelende dien bodem in ettelicke euen deelen (die wy maten noemen) met linien euewydich van AB, ick neem ten eersten in tween, mette lini GH, sniende EF in I, ende t'punt K sy alsoo, dat EK dobbel is an KF, welcke K wy bewysen moeten t'swaerheyts middelpunt des gheprangs te sijn aldus:
Laet ABCD een bodem sijn, daer in ghetrocken is de lini EF, tusschen de middelen van AB, ende DC, deelende dien bodem in ettelicke euen deelen (die wy maten noemen) met linien euewydich van AB, ick neem ten eersten in tween, mette lini GH, sniende EF in I, ende t'punt K sy alsoo, dat EK dobbel is an KF, welcke K wy bewysen moeten t'swaerheyts middelpunt des gheprangs te sijn aldus:
 T' B E G H E E R D E. Wy moeten de grootheyt van A duer haer eyghenwicht vinden.
T' B E G H E E R D E. Wy moeten de grootheyt van A duer haer eyghenwicht vinden.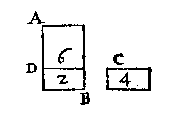 T' W E R C K. Ick teecken DB euegroot met C, de selue DB dan is het derdendeel van AB 6 lb, daerom DB weeght 2 lb, maer de stofswaerheyt van DB tot C, is als van 1 tot 2, daerom soo weeght C 4 lb.
T' W E R C K. Ick teecken DB euegroot met C, de selue DB dan is het derdendeel van AB 6 lb, daerom DB weeght 2 lb, maer de stofswaerheyt van DB tot C, is als van 1 tot 2, daerom soo weeght C 4 lb. laet A weghen 6 lb, ende groot sijn 5 voeten; ende t'ghewicht van B sy onbekent, maer huer grootheyt is van 2 voeten, ende de reden der stofswaerheyt van A tot B, sy van 4 tot 7. Nu om t'onbekende ghewicht van B te vinden, ick vergaer reden der stofswaerheyt, dat is Reden 4/7 tot reden der grootheyt, dat is Reden 5/2, comt reden des ghewichts Reden 10/7, t'ghewicht dan van A heeft sulcken reden tottet ghewicht van B, als 10 tot 7, maer A weeght 6 lb, daerom seg ick 10 gheeft 7, wat 6 lb ? comt voor t'ghewicht van B 4 1/5 lb.
laet A weghen 6 lb, ende groot sijn 5 voeten; ende t'ghewicht van B sy onbekent, maer huer grootheyt is van 2 voeten, ende de reden der stofswaerheyt van A tot B, sy van 4 tot 7. Nu om t'onbekende ghewicht van B te vinden, ick vergaer reden der stofswaerheyt, dat is Reden 4/7 tot reden der grootheyt, dat is Reden 5/2, comt reden des ghewichts Reden 10/7, t'ghewicht dan van A heeft sulcken reden tottet ghewicht van B, als 10 tot 7, maer A weeght 6 lb, daerom seg ick 10 gheeft 7, wat 6 lb ? comt voor t'ghewicht van B 4 1/5 lb.