[ 32 ]

X.   V E R T O O C H.      X I I.   V O O R S T E L.   W E S E N D E  een gheschickt bodem diens hoochste punt onder t'waters oppervlack is: T'ghewicht daer teghen rustende is euen anden pilaer waters diens grondt euen is an dien bodem, ende hoochde de hanghende lini {Perpendicularis.} van t'plat {Plano.} duer t'waters oppervlack, tot des bodems hoochste punt, ende bouen dien den helft der hanghende lini van des bodems hoochste punt, tottet plat euewydich vanden sichteinder {Horizonte.} duer des bodems leeghste punt.

[ 33 ]

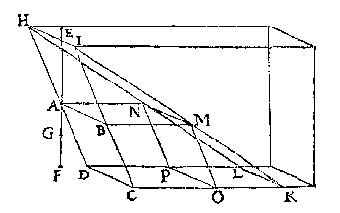
I   V O O R B E E L T.   T' G H E G H E V E N.   Laet ABCD een gheschickt bodem sijn, als ten eersten een euewydich vierhouck diens hoochste sijde AB onder t'waters oppervlack is, euewydich neem ick, vanden sichteinder, ende EA sy de hanghende lini van t'waters oppervlack, tot des bodems hoochste punt A, ende AF de hanghende lini van A, tot het plat euewydich Vanden sichteinder duer DC, ende AG sy den helft van AF.

T' B E G H E E R D E.   Wy moeten bewysen dattet ghewicht waters teghen den bodem ABCD rustende, euen is anden pilaer diens grondt dien bodem is ende hoochde GE.   T' B E R E Y T S E L.   Laet DA ende CB voortghetrocken worden tot H ende I, beyde in t'waters oppervlack; laet oock ghetrocken sijn HI, daer naer CK euewydich vanden sichteinder, ende euen an CI, maer rechthouckich op DC, sghelijcx DL euen ende euewydighe met CK, voort LK, daer naer IK ende HL, voort BM euewydighe met CK, ende also dat M inde lini IK sy, daer naer AN euen ende euewydighe met BM, voort MO ende NP beyde euen ende euewydighe met BC. 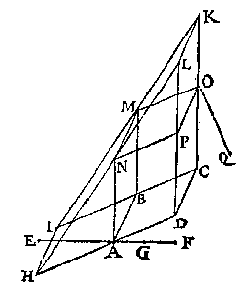     Laet daer na een ander form ghestelt worden, euen, ghelijck ende euewichtich mettet water euen ande voorgaende CDHIKL, maer also dat CK rechthouckich sy opden sichteinder als hier neuen.   T' B E W Y S.   Alsulcken drucksel als t'stijflichaem CDHIKL der tweede form, veroirsaeckt teghen den bodem CDHI, euen soodanighen drucksel veroirsaeckt t'water des eersten forms teghen sijn bodem CDHI so bewesen is int 11e voorstel ende veruolghens sulcken drucksel alsser valt teghen het deel ABCD der tweede form, euen soodanighen drucksel valter oock teghen het deel ABCD der eerste form, maer het drucksel teghen ABCD der tweede form is t'lichaem ABCDLKMN, t'welck euen is anden pilaer diens bodem ABCD ende hoochde GE, ghelijck wy terstont segghen sullen,

Ick seg dattet ghewicht waters teghen den bodem AB rustende, euen is anden pilaer waters diens bodem euen is ande selue AB, ende hoochde EC, waer af t'bewys sijn sal als van t'voorgaende.      T' B E S L V Y T.   Wesende dan een gheschict bodem diens hoochste punt, &c. M E R C K T.   Wy hebben hier bouen bethoont t'ghewicht teghen een gheschickt bodem rustende, mettet behulp der hanghende lini duer des bodems hoochste punt; Maer alst een ongheschickt bodem is, soo en wort dat ghewicht duer die hanghende lini niet bekent: Tis wel waer, datter altijt voor al op rust t'ghewicht euen an den pilaer waters diens grondt den bodem is, ende hoochde de hanghende lini van t'waters oppervlack tot des bodems hoochste punt, maer t'ander deel en is niet euen anden helft des pilaers wiens grondt dien bodem is, ende hoochde de hanghende lini van des bodems hoochste punt, tottet plat euewydich vanden sichteinder duer des bodems leeghste punt, waer af d'oirsaeck is, dat den pilaer met een ongheschickt bodem niet nootsakelick in twee euen deelen (ghelijck den pilaer met een gheschickt bodem) ghedeelt en wort, met een plat, duer twee lijckstandighe punten schoens teghen ouer malcander staende inde omtrecken der bodems. Maer op dat wy t'ghewicht teghen alle ongheschickt plat bodem oock bekent maken, sullen daer af soodanighen eysch beschrijuen. I I I   E Y S C H.           X I I I   V O O R S T E L.   W E S E N D E  in t'water een platte bodem van form soot valt: Te vinden een lichaem waters eueswaer an t'ghewicht teghen dien bodem rustende.   T' G H E G H E V E N.   Laet AB een platte bodem in t'water sijn, gheschickt ofte ongheschickt soot valt.   T' B E G H E E R D E.   Wy moeten een lichaem waters vinden eueswaer an t'ghewicht rustende teghen AB.   T' W E R C K.   Ick treck het plat AB ouer allen sijden oneindelick voort, diens ghemeen sne mettet waters oppervlack sy C, uyt de selue sne C treck ick een lini duer t plat AB als CD, maer alsoo dattet plat rechthouckich opden sichteinder duer CD, oock rechthouckich sy op t'oneindelick plat duer den ghegheuen bodem; Daernaer treck ick de lini DE, euen ande lini DC, maer euewydich vanden sichteinder,

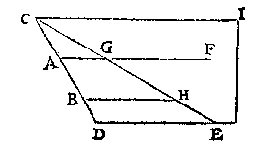ende rechthouckich op de lini die in t'oneindelick plat duer D oock euewydich vanden sichteinder is; Daer naer treck ick duer de ghemeen sne C, ende duer E, een oueral oneindelick plat CE; voort, uyt eenich punt vanden omtreck des ghegheuen bodems als uyt A, een oneindelicke lini AF, draeyende de selue mettet punt A in des bodems AB omtreckt, tot datse weder ter plaets comt daerse begon te roeren, maer alsoo datse int roeren altijt euewydich blijft met de lini DE, beschrijuende alsoo een lichaem begrepen tusschen de twee oneindelicke platten. ende t'vlack van die roerlicke lini beschreuen, als t'lichaem AGHB. Ick seg dat een lichaem waters euegroot an t'lichaem AGHB, eueswaer is an t'ghewicht rustende teghen den ghegheuen bodem. 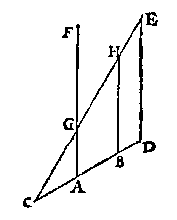    T' B E R E Y T S E L.   Laet beschreuen sijn dese tweede form euen ende ghelijck an d'eerste, ende eueswaer an water, maer also dat de lini DE rechthouckich sy opden sichteinder.   T' B E W Y S.   Alsulcken ghewicht alsser rust teghen den bodem AB der tweede form, euen soodanighen ruster oock teghen den bodem AB van d'eerste, als vooren bewesen is, maer teghen AB der tweede form, rust het ghewicht des lichaems AGHB, daerom teghen den bodem AB der eerste form, rust oock een ghewicht euen an t'lichaem waters AGHB, t'welck wy bewysen moesten.   T' B E S L V Y T.   Wesende dan int water een platte bodem van form soot valt, wy hebben een lichaem waters gheuonden eueswaer an t'ghewicht teghen dien bodem rustende, naer den eysch. X I.   V E R T O O C H.           X I I I I.   V O O R S T E L.   W E S E N D E  twee euewydighe vierhouckighe bodems van euen breeden, ende euediep int water, ende haer hoochste sijden int waters oppervlack: Ghelijck der bodems langde tot langde, alsoo haer gheprang des waters, tot gheprang des waters.

T' G H E G H E V E N.   Laet ABCD een water sijn, daer in twee euewydighe vierhouckighe bodems wesende, EF ende GH, van euen breeden, ende euediep int water, te weten, dat de hanghende {Perpendicularis.} IF, euen sy ande hanghende KH, ende haer hoochste sijden E en G, sijn int waters oppervlack. 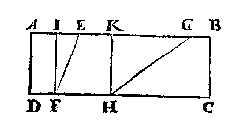     T' B E G H E E R D E.   Wy moeten bewysen dat ghelijck de langde EF, tot de langde GH, also t'gheprang des wtaers teghen den bodem EF, tottet gheprang des waters teghen den bodem GH.   T' B E W Y S.   T'ghewicht des waters teghen den bodem EF rustende, is euen anden helft des pilaers waters diens hoochde IF, ende grondt het plat EF, duer het 11e voorstel; Sghelijcx is t'ghewicht des waters teghen den bodem GH rustende, euen anden helft des pilaers waters diens hoochde KH, ende grondt het plat GH: maer dit sijn twee pilaren met euen hoochden daerom {32. v. II. B. E.} sijnse inde reden haerder gronden; maer ghelijck de langde EF, totte langde GH, alsoo den grondt EF, totten grondt GH, want sy duer tghestelde {Per hypothesin.} van euen breeden sijn, daerom ghelijck de langde EF totte langde GH, alsoo diens pilaer tot desens pilaer, ende wyder alsoo diens haluen pilaer tot desens haluen pilaer, ende veruolghens alsoo diens ghewicht des waters teghen haer rustende, tot desens ghewicht des waters teghen haer rustende.   T' B E S L V Y T.   Wesende dan twee euewydighe vierhouckighe bodems, van euen breeden, ende euediep int water, ende haer hoochste sijden int waters oppervlack: Ghelijck der bodems langde tot langde, also haer gheprang des waters, tot gheprang des waters, t'welck wt bewysen moesten. I I I I   E Y S C H.           X V   V O O R S T E L.   W E S E N D E  den bodem des waters een euewydich vierhouck oneuewydich vanden sichteinder {Horizonte.}, met sijn bekende hoochste sijde in t'waters oppervlack, ende bekent wesende de lini vande hoochste sijde rechthouckich op de voortghetrocken leeghste, oock de hanghende {Perpendicularis.} vande hoochste sijde tot het plat {Plano.} euewydich vanden sichteinder duer de leeghste sijde: Te vinden t'ghewicht waters daer teghen rustende.

M E R C K T.   A L L E euewydich vierhouck [on]euewydich vanden sichteinder met siin hoochste siide int waters oppervlack, is of rechthouckich of scheefhouckich, ende elck van desen is op den sichteinder rechthouckich oft scheefhouckich, daerom vallender vier verscheyden ghestalten, daer wy so wel inde volghende twee voorstellen als in dit, vier voorbeelden af beschrijuen sullen: T'eerste van een rechthouc opden sichteinder rechthouckich, wiens drie linien, als de siide oneuewydich vanden sichteinder, ende de lini uyt het uyterste vande hoochste siide rechthouckich opde voortghetrocken leeghste siide, ende de hanghende uyt het uyterste vande hoochste siide tottet plat euewydich vanden sichteinder duer de leeghste siide, al een selfde lini siin: Het tweede voorbeelt sal siin van een euewydich scheefhouckich vierhouck opden sichteinder rechthouckich, diens twee linien als de lini vande hoochste siide rechthouckich op de leeghste siide, ende de hanghende vande hoochste siide tottet plat euewydich vanden sichteinder duer de leeghste siide, beyde een selue siin: Het derde voorbeelt sal siin van een rechthouck scheefhouckich opden sichteinder, diens twee linien, als de siide oneuewydich vanden sichteinder, ende de lini van t'uyterste der hoochste siide rechthouckich op de leeghste siide, beyde een selue siin: T'vierde voorbeelt van een euewydich scheefhouckich vierhouck opden sichteinder scheefhouckich, diens voornoemde drie linien al verscheyden siin. Ie   V O O R B E E L T.   T' G H E G H E V E N.   Laet ABCD een rechthouck wesen rechthouckich opden sichteinder, diens sijde AB in t'waters oppervlack doe 4 voeten, ende AD 3 voeten. 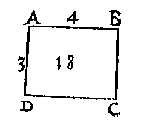    T' B E G H E E R D E.   Wy moeten t'ghewicht waters vinden rustende teghen ABCD.   T' W E R C K.   Ick menichvuldighe 3 van AD duer 4 van AB, maeckt 12, die andermael ghemenichvuldigt duer 3 van AD comt 36 voeten, diens helft voor t'begheerde 18 voeten. Ofte andersins ick menichvuldighe t'vircant der 3 van AD, duer den helft der 4 van AB, comt als vooren 18 voeten. nu ghenomen den voet te weghen 65 lb, soo ruster 1170 lb teghen. I Ie   V O O R B E E L T.   T' G H E G H E V E N.   Laet ABCD een euewydich scheefhouckich vierhouck wesen, rechthouckich op den sichteinder, diens sijde AB in t'waters oppervlack doe 4 voeten, ende AE hanghende lini vande hoochste sijde AB, tot inde voortghetrocken CD, sy van 3 voeten.

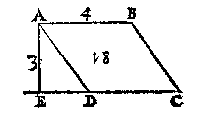T' B E G H E E R D E.   Wy moeten t'ghewicht waters vinden rustende teghen ABCD.   T' W E R C K.   Ick menichvuldighe 3 van AE duer 4 van AB, maeckt 12, die andermael ghemenichvuldigt duer 3 van AE comt 36 voeten, diens helft voor t'begheerde 18 voeten. Oft andersins ick menichvuldighe als bouen t'viercant der 3 met den helft der 4 van AB. I I I.   V O O R B E E L T.   T' G H E G H E V E N.   Laet ABCD een rechthouck wesen 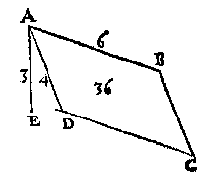scheefhouckich op den sichteinder, diens sijde AB in t'waters oppervlack sijnde doet 6 voeten, ende AD 4 voeten, maer AE hanghende van A tot in t'plat euewydich vanden sichteinder duer DC doe 3 voeten.   T' B E G H E E R D E.   Wy moeten t'ghewicht waters vinden teghen ABCD rustende.   T' W E R C K.   Ick menichvuldighe 4 duer 6 comt 24, de selue duer 3 maeckt 72 voeten, diens helft voor t'begheerde 36 voeten. Ofte andersins ick menichvuldighe den uytbreng van 3 met 4, duer den helft van 6, comt als vooren 36 voeten. I I I Ie   V O O R B E E L T.   T' G H E G H E V E N.   Laet ABCD een euewydich scheefhouckich vierhouck sijn, 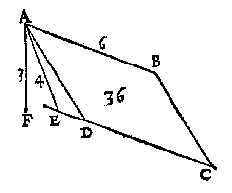scheefhouckich opden sichteinder, diens sijde AB in t'waters oppervlack sijnde doet 6 voeten, ende AE rechthouckich op de voortghetrocken CD doet 4 voeten, ende AF hanghende van A tot het plat euewydich vanden sichteinder duer DC doet 3 voeten.   T' B E G H E E R D E.   Wy moeten t'ghewicht waters vinden teghen ABCD rustende.   T' W E R C K.   Ick menichvuldighe 4 van AE, met 6 van AB comt 24, t'selue met 3 van AF, comt 72 voeten, diens helft voor t'begheerde 36 voeten. Ofte andersins, ick menichvuldighe, als vooren, den uytbreng van 3 met 4, duer den helft van 6, comt oock 36 voeten.

T' B E W Y S.   Wesende een pilaer diens grondt 12 voeten, ende hoochde 3 voeten, den helft van dien doet 18 voeten; maer sulcken lichaem ruster teghen den bodem ABCD des Ien voorbeelts, duer het 11e voorstel, daer rust dan t'ghewicht van 18 voeten waters teghen. Sghelijcx sal oock t'bewys sijn van d'ander voorbeelden.   T' B E W Y S.   Wesende dan den bodem des waters een euewydich vierhouck, &c. I   V E R V O L G H.      Uyt het boue­schreuen is blijckelick, hoemen vinden sal t'ghewicht waters teghen een euewydich vierhouck rustende, wesende d'hoochste sijde des ghegheuen vierhoucx onder t'waters oppervlack, want tot het ghewicht gheuonden alsvooren, noch vergaert den pilaer diens grondt dien bodem is, ende hoochde de hanghende lini van t'plat duer t'waters oppervlack tot de hoochste sijde des bodems, de somme sal t'begheerde sijn.   Laet by voorbeelt ABCD een euewydich vierhouck sijn oneuewydich vanden sichteinder, diens hoochste sijde AB onder t'waters oppervlack EF is, ende GA doende drie voeten sy de hanghende lini van t'plat duer EF tot de sijde AB, ende t'plat ABCD sy groot 20 voeten, ende als AB in t'waters oppervlack waer, soo souder op rusten (t'welck ick neem gheuonden te sijne duer de voorgaende leering) 40 voeten waters: Vraegh hoe veel datter nu op rusten? Ick menichvuldighe 20 des plats van ABCD, duer 3 van GA, comt een pilaer van 60 voeten, die tot de 40 maeckt 100 voeten dieder teghen ABCD rusten. I I.   V E R V O L G H.   Soo den ghegheuen platten bodem ongheschickt waer, men sal vinden een lichaem waters eueswaer an t'ghewicht teghen dien bodem rustende duer het 13e voorstel, t'selue lichaem ghemeten sal de begheerde swaerheyt bekent maken. V   E Y S C H.           X V I   V O O R S T E L.   W E S E N D E  den bodem des waters een euewydich vierhouck, oneuewydich vanden sichteinder {Horizonte.}, met sijn hoochste sijde int waters oppervlack, ende bekent sijnde t'ghewicht daer teghen rustende,

oock de lini vande hoochste sijde rechthouckich opde voortghetrocken leeghste sijde, mette hanghende {Perpendiculari.} vande hoochste sijde, tottet plat {Planum.} euewydich vanden sichteinder duer de leeghste sijde: D'hoochste sijde bekent te maken. 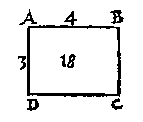I   V O O R B E E L T.     T' G H E G H E V E N.   Laet ABCD een rechthouck wesen rechthouckich opden sichteinder, daer teghen rustende t'ghewicht van 18 voeten waters, ende d'hoochste sijde AB in t'waters oppervlack sy onbekent, maer AD doet 3 voeten.   T' B E G H E E R D E.   Wy moeten de sijde AB bekent maken.   T' W E R C K.   Ick deel de 18 duer t'viercant der 3 van AD comt 2 voeten, diens dobbel voor AB 4 voeten. 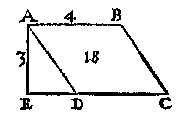I I   V O O R B E E L T.     T' G H E G H E V E N.   Laet ABCD een euewydich scheefhouckich vierhouck wesen, rechthouckich opden sichteinder, daer teghen rustende t'ghewicht van 18 voeten waters, ende d'hoochste sijde AB in t'waters oppervlack si onbekent, maer de lini AE vande hoochste sijde rechthouckich opde voortghetrocken leeghste sijde doet 3 voeten.   T' B E G H E E R D E.   Wy moeten de sijde AB bekent maken.   T' W E R C K.   Ick deel de I8 duer t'viercant der 3 van AE comt 2 voeten, diens dobbel voor AB 4 voeten. 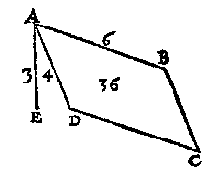I I I   V O O R B E E L T.     T' G H E G H E V E N..   Laet ABCD een rechthouck wesen scheefhouckich opden sichteinder, daer teghen rustende t'ghewicht van 36 voeten waters, ende d'hoochste sijde AB in t'waters oppervlack sy onbekent, maer de lini AD doet 4 voeten, ende AE hanghende vande hoochste sijde tot het plat euewydich vanden sichteinder duer de leeghste sijde doet 3 voeten.   T' B E G H E E R D E.   Wy moeten de sijde AB bekent maken.   T' W E R C K.   Ick menichvuldighe 3 van AE duer 4 van AD comt 12, daer duer ghedeelt de 36 comt 3 voeten, diens dobbel voor AB 6 voeten.

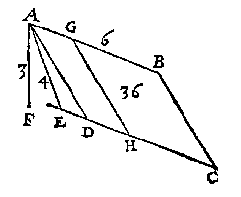I I I Ie   V O O R B E E L T.     T' G H E G H E V E N..   Laet ABCD een euewydich scheefhouckich vierhouck sijn scheefhouckich opden sichteinder, daer teghen rustende t'ghewicht van 36 voeten waters, ende d'hoochste sijde AB in t'waters oppervlack sy onbekent, maer AE lini vande hoochste sijde rechthouckich op de voortghetrocken leeghste sijde CD, doet 4 voeten, ende AF hanghende vande hoochste sijde tot het plat euewydich vanden sichteinder duer de leeghste sijde, doet 3 voeten.   T' B E G H E E R D E.   Wy moeten de sijde AB bekent maken.   T' W E R C K.   Ick menichvuldighe 3 van AF, met 4 van AE, comt 12, daer duer ghedeelt de 36, comt 3 voeten, diens dobbel voor AB 6 voeten.   T' B E W Y S.   Soo AB des Ien voorbeelts langher of corter waer als 4 voeten, t'ghewicht waters teghen den bodem rustende soude moeten meerder of minder sijn dan 18 voeten, t'welck teghen t'ghestelde waer, daerom AB is van 4 voeten. Sghelijcx sal oock t'bewys sijn van d'ander voorbeelden.   T' B E S L V Y T.   Wesende dan den bodem des waters een euewydich vierhouck oneuewydich, &c. I   V E R V O L G H.   Uyt het voorgaende is blijckelick, hoemen d'hoochste sijde bekent sal maken, als sy onder t'waters oppervlack is, want van t'gheheel ghewicht waters teghen den bodem rustende, ghetrocken den pilaer diens grondt dien bodem is, ende hoochde de hanghende lini van t'plat duer t'waters oppervlack tot de hoochste sijde des bodems, daer sal resten t'ghewicht waters opden bodem rustende als haer hoochste sijde in t'waters oppervlack is, waer duer sy alsdan bekent sal worden als vooren gheleert is. I I   V E R V O L G H.   Soomen inden bodem een lini wilde trecken euewydich met de sijde die vanden sichteinder oneuewydich is, de noodighe langde der hoochste sijde can bekent worden. Laet by voorbeelt inde form des boueschreuen 4en voorbeelts, te trecken sijn een lini als GH, euewydich met AD, alsoo dat op AGHD ruste t'ghewicht van 12 voeten waters. Ick sie wat deel dese 12 sijn vande 36 dieder teghen rusten, wort beuonden het derdedeel, daerom oock sal AG 1/3 wesen van AB dat sijn 2 voeten.