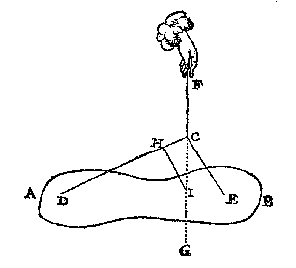
Weerom BN gheeft MN, wat T'ghewicht G? T'ghene daeruyt volght is voor t'ghewelt op BC ancommende.
Laet andermael HC voorwaert ghetrocken worden tot O, en BP evewijdeghe met CD: Ick segh CP gheeft CB, wat t'ghewicht H? T'gene daer uyt comt is voor t'ghewelt op BC ancommende. Waer uyt blijckt datmen alsdan t'selve sal moeten vinden, datmen te vooren van BC vant: En soo voort met al d'ander. Hier af en van meer ander heeft sijn V O R S T E L I C K E G H E N A D E dadelicke proef ghedaen, en bevonden die gantschelick t'overcommen mette spiegheling {Theoria.}.
De everedenheyt des 27 voorstels can deur ander manier uyt gesproken worden dan daer gedaen is, waer uyt lichter wercking volght. Om t'welck by voorbeelt te verclaren, laet hier andermael gestelt worden de form des selven 27 voorstels, alwaermen seght, ghelijck scheefhefwicht tot rechthefwicht, also elck scheefhefwicht [-lijn] tot sijn rechthefwicht [-lijn].
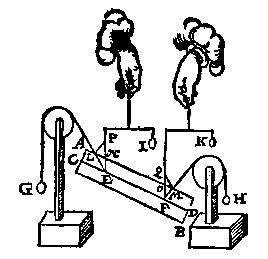 Maer om dit deur ander manier uyt te spreken, waer uyt lichter wercking volght; ick treck tusschen rechtheflijn en scheefheflijn, een lini als LP evewijdighe met FM: T'welck soo wesende, ick segh nu, ghelijck rechtheflijn tot scheefheflijn, alsoo t'ghewicht des heelen pylaers, tot haer scheefhefwicht, dat is, ghelijck EP tot EL, alsoo t'ghewicht des pylaers tot G. Wederom ghelijck EP tot PL, alsoo t'ghewicht des pylaers tot H: Na welcke manier het vinden der onbekende palen openbaerlick corter valt, als na d'ander. Merckt noch datmen in plaets van LP, oock soude hebben meughen trecken een lini tusschen d'ander rechtheflijn en haer scheefheflijn, als hier MQ evewijdeghe met EL, waer me men dergelijcke soude meughen doen als met LF gedaen is, en tot een selve besluyt commen: Want ghelijck PE tot EL, alsoo QF tot FM, uyt oirsaeck dat den driehouck FMQ, even en gelijck is met LPE, deur dien QF evewijdeghe is met PE, en MF met LP.
Maer om dit deur ander manier uyt te spreken, waer uyt lichter wercking volght; ick treck tusschen rechtheflijn en scheefheflijn, een lini als LP evewijdighe met FM: T'welck soo wesende, ick segh nu, ghelijck rechtheflijn tot scheefheflijn, alsoo t'ghewicht des heelen pylaers, tot haer scheefhefwicht, dat is, ghelijck EP tot EL, alsoo t'ghewicht des pylaers tot G. Wederom ghelijck EP tot PL, alsoo t'ghewicht des pylaers tot H: Na welcke manier het vinden der onbekende palen openbaerlick corter valt, als na d'ander. Merckt noch datmen in plaets van LP, oock soude hebben meughen trecken een lini tusschen d'ander rechtheflijn en haer scheefheflijn, als hier MQ evewijdeghe met EL, waer me men dergelijcke soude meughen doen als met LF gedaen is, en tot een selve besluyt commen: Want ghelijck PE tot EL, alsoo QF tot FM, uyt oirsaeck dat den driehouck FMQ, even en gelijck is met LPE, deur dien QF evewijdeghe is met PE, en MF met LP.
8 V E R V O L G H.
Tot hier is gheseyt van ghewichten hanghende an twee linien: Int volghende willen wy handelen van ghewichten an meer dan twee linien hangende:
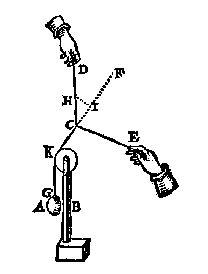 Tot desen eynde segh ick aldus:
Tot desen eynde segh ick aldus:
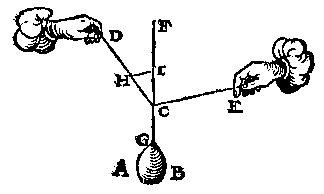
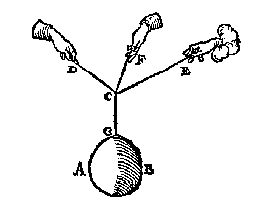
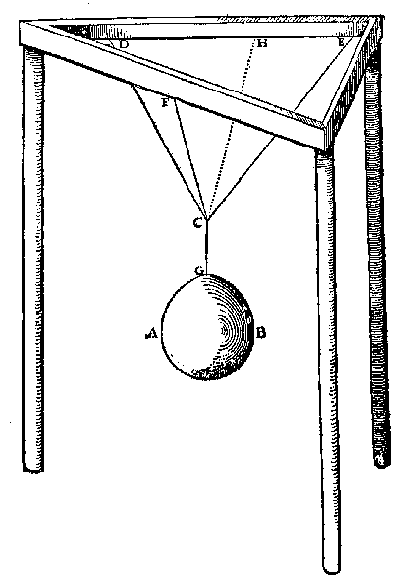
Laet ons andermael nemen de form des 5 vervolghs, welcke sy de onderschreven deses 8 vervolghs, alleenelick daer in verschillende, dat de lini CG hier comt over een catrol an K, sulcx dat hoewel KCF een rechte lini is, nochtans comtse scheefhouckich op den sichteinder: Voort sy dit ghewicht AB t'selve, en de twee houcken DCF, FCE oock de selve. Dit soo wesende, tis kennelick dat wy hier meughen seggen als int 5 vervolgh, ghelijck CI tot CH, alsoo t'ghewicht AB tottet ghewicht op D ancommende: Voort ghelijck CI, tot IH, alsoo t'ghewicht AB tottet ghewicht op E ancommende: Weerom ghelijck CH, tot HI, also t'ghewicht op D ancommende, tottet ghewicht op E ancommende.
Hier uyt is openbaer dat sooder an een lini DCE als coorde, hinghe een gewicht AB, datmen can segghen hoe veel ghewelt elck deel DC, CE, te doen heeft.
9 V E R V O L G H.
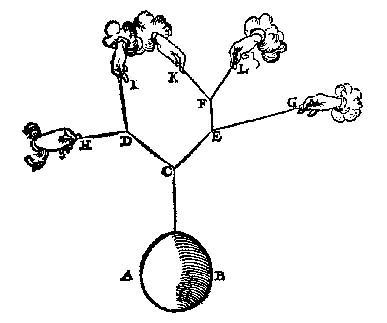
Soo een ghewicht hinghe an drie linien, als hier onder, t'ghewicht AB hanghende ande twee linien CD, CE, maer de selve CE ande twee linien EF, FG, sulcx dattet ghewicht AB hangt ande drie linien CD, EF, EG, men can weten hoe veel ghewelt datter op elcke der selve drie linien ancomt.
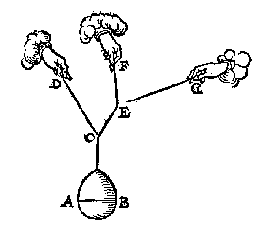 Want deur het 5 vervolgh is openbaer watter op CD en CE ancomt: Maer bekent wesende wat ghewelt op CE ancomt, soo wort deur het 8 vervolgh gheweten watter op elcke der twee linien EF, EG, ancomt.
Want deur het 5 vervolgh is openbaer watter op CD en CE ancomt: Maer bekent wesende wat ghewelt op CE ancomt, soo wort deur het 8 vervolgh gheweten watter op elcke der twee linien EF, EG, ancomt.
Maer sooder ande lini CD hier boven ghehecht waren sulcke twee treckende linien als an CE, ghelijck hier onder DH, DI, tis openbaer dattet ghewicht an yder dier twee linien, alsoo bekent soude worden ghelijck over d'ander sijde, en vervolghens dat bekent soude sijn hoe veel ghewelt op yder der vier linien EF, EG, DH, DI ancomt, t'sy oock dat de linien als DH en EF met dierghelijcke, commen in een selve plat of niet.
 Y sijn na d'eerste beschrijving der Weeghconst, verscheyden stoffen der wichtighe ghedaenten voorghecommen, soo in spiegheling als daet {Theoria quam praxi.}, diemen in dese tweede druck elck t'haerder plaets van d'eerste oirden soude hebben meughen schicken, om daer af een verknocht lichaem te maken:
Y sijn na d'eerste beschrijving der Weeghconst, verscheyden stoffen der wichtighe ghedaenten voorghecommen, soo in spiegheling als daet {Theoria quam praxi.}, diemen in dese tweede druck elck t'haerder plaets van d'eerste oirden soude hebben meughen schicken, om daer af een verknocht lichaem te maken:  Y hebben inde drie laetste voorstellen des I boucx der Weeghconst, beschreven de wichtighe ghedaenten van swaerheden hangende an twee linien, gehecht ant lichaem tot twee verscheyden plaetsen. Maer want de swaerheden op meer ander wijsen an linien connen hanghen, waer afmen oock begheert te weten wat ghewelt op yder lini ancomt, soo hebben wy daer af dese besonder handel ghemaeckt:
Y hebben inde drie laetste voorstellen des I boucx der Weeghconst, beschreven de wichtighe ghedaenten van swaerheden hangende an twee linien, gehecht ant lichaem tot twee verscheyden plaetsen. Maer want de swaerheden op meer ander wijsen an linien connen hanghen, waer afmen oock begheert te weten wat ghewelt op yder lini ancomt, soo hebben wy daer af dese besonder handel ghemaeckt: 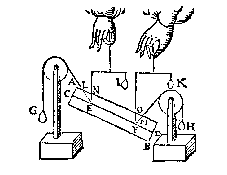
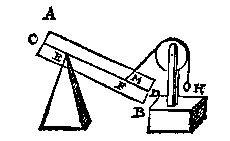
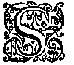 O O M E N inde form des 27 voorstels vant I bouck, an t'punt E, in plaets van het scheefwicht G, vervoughde een vastpunt als hier nevens, tis kennelick dat teghen dit vastpunt een persing soude sijn, even an t'ghewicht G, en dat met sulcken scheefheyt teghen t'selve punt E ancommende, als de scheef[hef]lijn LE anwijst.
O O M E N inde form des 27 voorstels vant I bouck, an t'punt E, in plaets van het scheefwicht G, vervoughde een vastpunt als hier nevens, tis kennelick dat teghen dit vastpunt een persing soude sijn, even an t'ghewicht G, en dat met sulcken scheefheyt teghen t'selve punt E ancommende, als de scheef[hef]lijn LE anwijst.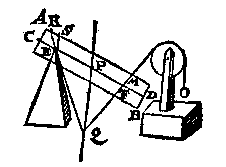 Daerom somen wilde weten wat scheve persing datter ancomt, opt vastpunt E des I vervolghs, men sal aldus meughen doen: Ick treck deur des pylaers swaerheyts middelpunt als P hier nevens, de oneyndelicke swaerheyts middellijn, welcke vande voortgetrocken MF, ontmoet wort in Q; daer na van Q deur E de lini QR, vallende R in AM. T'welck soo sijnde, de persing op E aancommende, is als van R na E, en om te weten hoe groot, men ghebruyckt int werck ER voor scheefheflijn, en ES voor rechtheflijn, waer me men openbaerlick tottet begheerde comt.
Daerom somen wilde weten wat scheve persing datter ancomt, opt vastpunt E des I vervolghs, men sal aldus meughen doen: Ick treck deur des pylaers swaerheyts middelpunt als P hier nevens, de oneyndelicke swaerheyts middellijn, welcke vande voortgetrocken MF, ontmoet wort in Q; daer na van Q deur E de lini QR, vallende R in AM. T'welck soo sijnde, de persing op E aancommende, is als van R na E, en om te weten hoe groot, men ghebruyckt int werck ER voor scheefheflijn, en ES voor rechtheflijn, waer me men openbaerlick tottet begheerde comt.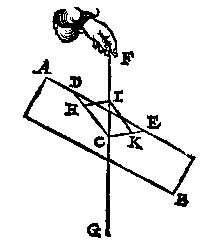 het swaerheyts middelpunt C; de selve CD en CE sijn swaerheyts middellijnen des pylaers deur de 5 bepaling:
het swaerheyts middelpunt C; de selve CD en CE sijn swaerheyts middellijnen des pylaers deur de 5 bepaling: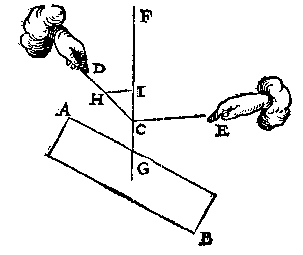
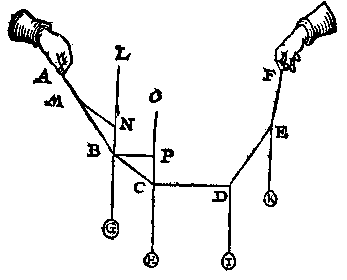
 Maer om dit deur ander manier uyt te spreken, waer uyt lichter wercking volght; ick treck tusschen rechtheflijn en scheefheflijn, een lini als LP evewijdighe met FM: T'welck soo wesende, ick segh nu, ghelijck rechtheflijn tot scheefheflijn, alsoo t'ghewicht des heelen pylaers, tot haer scheefhefwicht, dat is, ghelijck EP tot EL, alsoo t'ghewicht des pylaers tot G. Wederom ghelijck EP tot PL, alsoo t'ghewicht des pylaers tot H: Na welcke manier het vinden der onbekende palen openbaerlick corter valt, als na d'ander. Merckt noch datmen in plaets van LP, oock soude hebben meughen trecken een lini tusschen d'ander rechtheflijn en haer scheefheflijn, als hier MQ evewijdeghe met EL, waer me men dergelijcke soude meughen doen als met LF gedaen is, en tot een selve besluyt commen: Want ghelijck PE tot EL, alsoo QF tot FM, uyt oirsaeck dat den driehouck FMQ, even en gelijck is met LPE, deur dien QF evewijdeghe is met PE, en MF met LP.
Maer om dit deur ander manier uyt te spreken, waer uyt lichter wercking volght; ick treck tusschen rechtheflijn en scheefheflijn, een lini als LP evewijdighe met FM: T'welck soo wesende, ick segh nu, ghelijck rechtheflijn tot scheefheflijn, alsoo t'ghewicht des heelen pylaers, tot haer scheefhefwicht, dat is, ghelijck EP tot EL, alsoo t'ghewicht des pylaers tot G. Wederom ghelijck EP tot PL, alsoo t'ghewicht des pylaers tot H: Na welcke manier het vinden der onbekende palen openbaerlick corter valt, als na d'ander. Merckt noch datmen in plaets van LP, oock soude hebben meughen trecken een lini tusschen d'ander rechtheflijn en haer scheefheflijn, als hier MQ evewijdeghe met EL, waer me men dergelijcke soude meughen doen als met LF gedaen is, en tot een selve besluyt commen: Want ghelijck PE tot EL, alsoo QF tot FM, uyt oirsaeck dat den driehouck FMQ, even en gelijck is met LPE, deur dien QF evewijdeghe is met PE, en MF met LP. Tot desen eynde segh ick aldus:
Tot desen eynde segh ick aldus:  Want deur het 5 vervolgh is openbaer watter op CD en CE ancomt: Maer bekent wesende wat ghewelt op CE ancomt, soo wort deur het 8 vervolgh gheweten watter op elcke der twee linien EF, EG, ancomt.
Want deur het 5 vervolgh is openbaer watter op CD en CE ancomt: Maer bekent wesende wat ghewelt op CE ancomt, soo wort deur het 8 vervolgh gheweten watter op elcke der twee linien EF, EG, ancomt.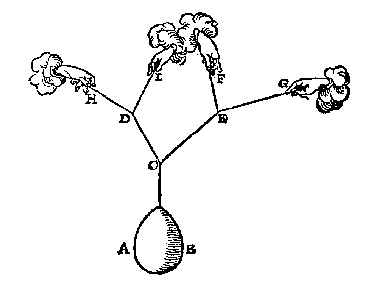
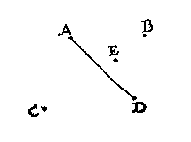 Maer inde lini AD vallende, tis kennelick dat de ghewelt der twee linien onder B en C commende, wel meughen verlichten de ghewelt der twee linien onder A en D commende, maer de ghestalt des driehoucx dier twee linien, te weten de twee onder A en D, mette derde AD, en crijcht gheen verandering: En daerom meughen oneyndelicke verscheyden grooter en cleender ghewelden ande linien onder C, B, vervought worden, dei de ghewelden op A en D ancommende veranderen, blijvende nochtans de form van t'ghegheven de selve, sulcx datter gheen seker eenich besluyt en is.
Maer inde lini AD vallende, tis kennelick dat de ghewelt der twee linien onder B en C commende, wel meughen verlichten de ghewelt der twee linien onder A en D commende, maer de ghestalt des driehoucx dier twee linien, te weten de twee onder A en D, mette derde AD, en crijcht gheen verandering: En daerom meughen oneyndelicke verscheyden grooter en cleender ghewelden ande linien onder C, B, vervought worden, dei de ghewelden op A en D ancommende veranderen, blijvende nochtans de form van t'ghegheven de selve, sulcx datter gheen seker eenich besluyt en is.