Chr. Huygens: meetkunde-problemen 1645

Meetkunde-problemen, 1645

Inleiding
Christiaan Huygens werd in 1645 zestien jaar. Het vorige jaar waren de wiskundelessen begonnen, die hij en zijn oudere broer Constantijn kregen van Jan Jansz Stampioen de Jonge. Deze had op papier gezet welke wiskundige werken bestudeerd moesten worden (zie studieadvies, OC I, 5). Het eerste daarvan was:
Sybrandt Hansz Cardinael, Hondert Geometrische questien met hare solutien, Amsterdam ca. 1612 *).

Stuk III bevat acht problemen °), waarvan verscheidene een sterke gelijkenis vertonen met 'questiën' van Cardinael. Overigens was 1645 ook het jaar waarin de broers hun studie aan de Leidse universiteit begonnen, waarbij Christiaan wiskundelessen kreeg van Frans van Schooten jr, professor aan de 'ingenieursschool' te Leiden.

Stuk IV handelt over kegelsneden.

*) Zie: J. van Maanen in NAW 5/4 nr. 1 (2003) 51-55.
En: M. H. Sitters, in NAW 5/4 nr. 4 (2003) 309-316; en in Gewina 27 (2004) 14-32.

°) Uit: Oeuvres Complètes, XI, 23-7. Vertaald uit het Latijn, met zoveel mogelijk gelijke opmaak, maar met het moderne gelijkheidsteken (Huygens gebruikte het teken

). De noten zijn deels verwerkt in de toelichtingen.

[ 23 ]

III. [1645]. 1. In een gegeven driehoek een ingeschreven cirkel beschrijven. Stel AB = a; BC = b; AC = c; DC = x. Aangezien dus EC gelijk is aan DC, zal gelden:
	BE = b – x
en wegens de gelijkheid van de stralen:
	AF = a – b + x
waaraan AD gelijk is, om dezelfde reden. Maak een vergelijking als volgt:
AD + DC	a – b + 2x	=	c	AC
	2x	=	c + b – a
	x	=	c + b – a 2
Neem dan EC gelijk aan DC, en het snijpunt van de loodlijnen EG en DG zal het middelpunt zijn van de in de driehoek ingeschreven cirkel. [ Constructie: - Zet op het verlengde van AC de lengte van CB, - zet de lengte van AB op AC (het cirkelboogje daarvoor is te zien), - neem het verschil van AC + CB en AB, en bepaal daarvan het midden (zie streepje). De lengte van het streepje tot B is dan de gezochte x, waaraan CD gelijk genomen wordt. ]

[ 24 ]

2. In een gegeven driehoek een gelijkzijdige driehoek beschrijven, zodanig dat één zijde evenwijdig is aan één zijde van de gegeven driehoek. Beschrijf eerst op de zijde AC een gelijkzijdige driehoek ALC, en daar omheen een rechthoek ANMC. Als ik nu in de gegeven driehoek een hieraan gelijkvormige rechthoek beschrijf, kan ik gemakkelijk daarin ook een gelijkzijdige driehoek beschrijven. Stel dan AC = a; AB = b, IB = c; BH = x, AN = d. En dan komt er:
b staat tot a, als x tot			xa b	ofwel HG.
En ook:
b staat tot c, als b – x tot			cb – cx b	ofwel HE.
Dus zal gelden, wegens gelijkvormige rechthoeken HF en AM:
vermenigv.	{	cb – cx b	HE HG	xa b
		a	AC AN	d
		cba – acx b	=	dxa b
cb	= dx + cx
cb d + c	= x
Constructie: Beschrijf op AC een gelijkzijdige driehoek, en trek de lijn BL; vanaf het punt D waar hij AC snijdt wordt DH evenwijdig met LA getrokken, en DH zal een zijde van de gevraagde driehoek zijn.

[ 25 ]

3.
In een gegeven cirkel een punt te vinden, zodanig dat, als er een lijn door getrokken wordt die binnen de cirkel blijft, en als er een loodlijn op een middellijn uit neergelaten wordt, dat het product van de lijnstukken waarin de loodlijn de basis verdeelt, gelijk is aan het kwadraat van de genoemde loodlijn samen met het product van de lijnstukken waarin dezelfde loodlijn een lijn verdeelt die door het gezochte punt getrokken wordt. ) Stel AC = a; ED = x; DC = y. En er zal gelden FH of HI = √(aa – xx) en EI = √(aa – xx) + y en FE = √(aa – xx*) – y. Dan zal, als ik vermenigvuldig, het product FEI worden:
	√(aa – xx) + y
maal	√(aa – xx) – y
	——————
product FEI	aa – xx – yy	} tel op
kwadr. DE	xx	} tel op
product FEI + kwadr. DE	aa – yy = aa – yy	product ADB.
Dit punt kan overal in de cirkel genomen worden, omdat van geen van beide de waarde gevonden wordt; en daarom is het een theorema. [ Toelichting: FH of HI = √(aa – xx) omdat FC = IC = a AD.DB = aa – yy omdat AD = a – y en DB = a + y De gelijkheid geldt ook voor de schuine lijn door G, want: - noem het snijpunt met de cirkel K, en trek FK en IG, - de driehoeken FEK en GEI zijn gelijkvormig (hoek KFI staat op dezelfde boog als hoek KGI), - dus FE : KE = EG : EI, zodat FE.EI = KE.EG. Theorema (omdat x en y er niet toe doen): Als op een middellijn van een cirkel een loodlijn wordt neergelaten vanuit een punt van een koorde, wordt deze middellijn verdeeld in lijnstukken waarvan het product gelijk is aan: het kwadraat van de loodlijn plus het product van de lijnstukken waarin dat punt de koorde verdeelt. ] ) Dit probleem, met de oplossing ervan, werd het eerste werk van Huygens dat gepubliceerd is, door van Schooten in Geometria à Renato Des Cartes* (1649, 203-5), als "gevonden door de weledele en doorluchtige jongeheer Christiaan Huygens, waarmee hij zich nu al enige tijd geleden bij de geleerden een zodanige lof en bewondering verschaft heeft, dat zij niet geaarzeld zullen hebben te verzekeren dat er nog enige grote dingen van hem te verwachten waren".

[ 26 ]

4.

Van een gegeven rechthoek een winkelhaak afsnijden van overal gelijke breedte, die de helft beslaat van de rechthoek zelf.

Stel AB = a; AC = b; AE = x.

Dan zal de winkelhaak tweemaal genomen gelijk zijn aan rechthoek AD, of:

2ax + 2bx – 2xx = ab
ax + bx – ½ ab = xx
½ a + ½ b – √( ¼ aa + ¼ bb) = x

IG is ½ a + ½ b,
FG of GH is √( ¼ aa + ¼ bb).
Dan is IH ½ a + ½ b – √( ¼ aa + ¼ bb), of x.

[ Toelichting:
De L-vorm is de winkelhaak (een stuk timmermansgereedschap).
Van de vierkantsvergelijking voldoet maar één oplossing, want x moet kleiner zijn dan a en b. ]

5.
Een gegeven driehoek middendoor snijden, vanuit een gegeven punt op een zijde.

Stel BC = a; DC = b; AC = c; EC = x.

Aangezien dus driehoek EDC de helft moet zijn van driehoek ABC, zal gelden:
vermenigv. { DC b
2 EC 2 x BC a
AC c
———— ———
2 x b = a c
x = a c
2 b

Dan geldt dus: b staat tot a, als ½ c tot x.

[ Toelichting:
D is gegeven punt, E wordt gezocht. De eerste gelijkheid volgt uit:
- de oppervlakte van een driehoek is: halve hoogte maal basis,
- voor driehoeken met een gelijke hoek is de hoogte evenredig met de schuine zijde aan die hoek,
- dus is de oppervlakte evenredig met: basis maal die schuine zijde.
Constructie:
Om nu E te vinden: trek BE evenwijdig DF, als F het midden van AC is. ]

[ 27 ]

Als ABC een gelijkbenige driehoek is, en als uit de top B een willekeurige BD wordt getrokken tot op de basis, zeg ik dat het product van AD en DC, samen met het kwadraat van DB, gelijk is aan het kwadraat van AB.
En daarom ook dat, hoe BD ook getrokken wordt, altijd de producten van de basis-lijnstukken, samen met het kwadraat van het uit de top getrokken lijnstuk, onderling gelijk zijn.

Dit volgt hier uit het 3^e probleem.

Toelichting:
Stel de punten A, B, C, D van deze figuur gelijk met de punten F, C, I, E van die bij probleem 3. Dan geldt:
product ADC = product FEI = aa – xx – yy,
kwadr. BD = kwadr. CE = xx + yy,
samen zijn ze aa, ofwel het kwadraat van AB.

7.

Een gegeven driehoek middendoor snijden met een lijn die evenwijdig is aan één van de zijden.

Stel AC = a; BC = b; EC = x.

a —— b —— x / bx
a
2x
ab = 2bxx
a
aa = 2xx
aa
2 = xx
√ aa
2 = x

Toelichting:
In de 2e regel zien we de 'regel van drie': a : b = x : ? Met de uitkomst ? = bx/a, ofwel DC.
[ Vermenigvuldiging met 2x levert ab, want (zie de toelichting bij probleem 5) de oppervlakten van driehoeken met een gelijke hoek verhouden zich als het product van de zijden aan die hoek.

Constructie: twee kwart-cirkels op AC, Pythagoras geeft x. ]

8.

Een gegeven driehoek door een punt binnen deze driehoek middendoor snijden.*)

*) In plaats van een oplossing staan er in het manuscript twee doorgekraste figuren. Frans van Schooten gaf twee oplossingen in een verzameling notities die door Huygens gebruikt zijn, en in 1651 gaf deze voor één ervan een bewijs (p. 14).
Van Schooten gaf een algemenere oplossing in Exercitationum mathematicarum ... van 1657, p. 107 [Ned. 1659, p. 107].

Het is de fameuze 'questie 92' van Cardinael (cf. Sitters, 315).
[ Zie wat Simon Stevin ervan zegt in de 'Meetdaet' (1605, 144): "seer spitsvondich", "niet by de Griecken bekent gheweest", en "dattet in deeling van landen somwijlen dadelick vereyscht wort". Hij nam eerst het punt buiten de driehoek, past een "stelreghelsche wercking" toe (p. 147 lidt 4), maar loste het probleem verder meetkundig op. ]

[ 28 ]

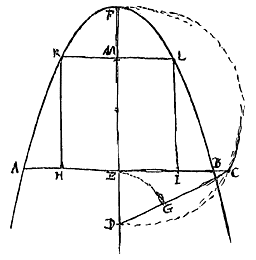
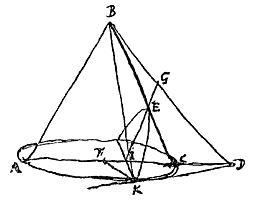
Stuk IV bevat verscheidene problemen, oplossingen en theorema's met betrekking tot kegelsneden. Ze kunnen rechtstreeks zijn ingegeven door het lezen van de Conica van Apollonius, genoemd op de lijst van Stampioen (T. I, p. 6); maar misschien ook door het onderwijs van Frans van Schooten.
Bij Stampioen wordt genoemd: Conicorum libri quattuor, 1566, zie daar prop. XI van boek 1. [Engl.]

IV.

[1645].

1.

Over het latus rectum van de Parabool en hoe dit wordt gevonden.

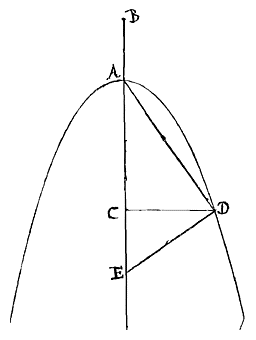
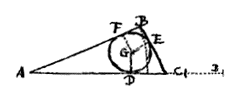
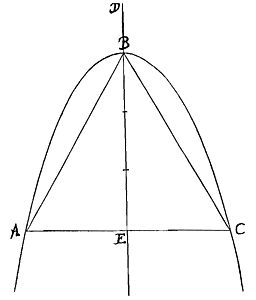
Als op de middellijn van een parabool ergens een punt wordt genomen, zoals hier C, en van daaruit wordt de loodlijn CD getrokken (die genoemd wordt ordinaatsgewijs aangebracht*)) is er een of andere lijn waarvan het product met de lijn AC steeds gelijk is aan het kwadraat van CD; deze lijn is vast en het is er één, en wordt genoemd het latus rectum van de parabool, zoals hier AB. Hieruit volgt dat AC steeds tot CD is als CD tot het latus rectum AB.

En daarom: als CD gelijk is aan AC zal elk van beide gelijk zijn aan het latus rectum.

Het latus rectum wordt dus gevonden als gemaakt wordt dat AC tot CD is als CD tot een vierde lijn. Dat wil zeggen door DE loodrecht op AD te trekken, zal CE altijd gelijk zijn aan het latus rectum, AB.

Zie Conicorum libri IV (1566, ed. Commandino), boek 1, Prop. XI, p. 13v. [Engl. 1896.]
[ Het latus rectum is de koorde door het brandpunt evenwijdig aan de richtlijn (loodrecht op de as), en gelijk aan het dubbele van de 'parameter', Zie ook: 'Paraboolconstante'. ]
[ *) Lat.: "ordinatim applicata". Zie Ma. Rosa Massa Esteve, 'Algebra and geometry in Pietro Mengoli (1625-1686)', in Historia Mathematica 33 (2006), 82-112, n.48: ]

Mengoli used the word "ordinata" instead of the word "applicata", which was commonly used at the time. Descartes defined the ordinates as "celles qui s'appliquent par ordre" [Descartes, 1954, 67]°). In the 1954 edition there is the following editorial note: "The equivalent of 'ordination application' was used in the 15th century on translating Apollonius." The note also states that Hutton's Mathematical Dictionary of 1796 gave "applicata" as the word corresponding to the ordinate and explained that the expression "ordinata applicata" was also used. In fact Fermat and Cavalieri used "applicata". Mengoli in Circolo [1672] named them "ordinatamente applicate" [Mengoli, 1672, 5].
[ °) Descartes 1637, p. 328. Het gaat om een loodlijn (normaal) op een diameter van een cirkel; de uitdrukking is te vertalen als "die volgens de norm worden aangebracht".]

[ Zie ook Egbert Buys, Nieuw en volkomen woordenboek van konsten en weetenschappen, deel 8 (1777), p. 252: "Ordinatae, of Ordinate applicates ... Parallel-Liniën ... eindigende in een kromme Linie, en verdeeld door een Diameter".]

[ 29 ]

2.

In een gegeven Parabool een gelijkzijdige driehoek beschrijven.

Laat BD het latus rectum zijn van de Parabool,

a. BE

x.

Dus zal gelden:

EC		√(ax), en
BC √(ax + xx)		2 √(ax) AC.
ax + xx		4 ax
xx		3 ax
x		3 a.

In een gegeven deel van een Parabool een vierkant beschrijven.

Neem FE a; latus rectum ED b;
HE x.
Dan zal ME 2 x zijn, en MF a – 2 x.
formules

[ Toelichting: volgens de definitie van het latus rectum is MF × DE = ML² .
Dit geeft de vergelijking: ab – 2 bx = x² die wij zouden oplossen met de 'abc-formule'.
Huygens doet het meetkundig: trek een halve cirkel op FD, dan geldt:
ab = FE × ED = EC² = DC² – ED² , dus: DC = √(ab + b²) , en: GC = DC – ED. ]

[ 30 ]

4.

Aan een Parabool EIK de raaklijn in punt K te vinden.

Stel je voor dat op de kegel een vlak BKD wordt gelegd, dat de kegel raakt in de rechte BK. KD raakt de basis van de kegel in punt K. We moeten dus vinden waar IG de lijn DB zal snijden.

Neem IE

a; AF en FC

b. Het latus rectum van de parabool

r; IG

x.

Dus omdat hoek FKD recht is, zoals ook FIK en KID, zal gelden: zoals FI tot IK is, zo is IK tot ID.*)

[ Zoals √(bb – ar) tot √(ar), zo is √(ar) tot ID. ]

Zoals IC tot IE, zo is AC tot AB.

[ Zoals b – √(bb – ar) tot a, zo is 2 b tot AB. ]

AF + FI + ID

AD.

[ b + (bb – ar) / √(bb – ar) + ar / √(bb – ar)

AD. ]

Zoals AD tot AB, zo is ID tot IG.

[ Zoals {b √(bb – ar) + bb} / √(bb – ar) tot 2 ab / {b – √(bb – ar)}, zo is ar / √(bb – ar) tot IG. ]

De tellers van de eerste en de tweede kunnen worden gedeeld door b, en de noemer van de eerste en de derde geschrapt omdat deze bij beide dezelfde is, en het zal alleen nodig zijn te vermenigvuldigen de tellers van de tweede en de derde [uitkomst: 2 aar] en dit product te delen door het product van de teller van de eerste en de noemer van de tweede.
Door dus te vermenigvuldigen b + √(bb – ar), teller van de eerste,
met b – √(bb – ar), noemer van de tweede, komt er ar.

Dus 2 a

[ *) Toelichting: IE maal latus rectum: ar = IK² , dus: FI = √(b² – ar).
Uit de eerste verhouding volgt: ID = ar / √(b² – ar).
Uit de tweede verhouding volgt: AB = 2 ab / {b – √(b² – ar)}.
Geef FI dezelfde noemer als ID, en er komt:
AD = b + b² / √(b² – ar), of onder één noemer: {b √(b² – ar) + b²} / √(b² – ar) en zo in de laatste verhouding. ]

Vgl. Conicorum libri IV (1566, ed. Commandino), boek 1, Prop. XXXIII, p. 24v [Engl. 1896]: Apollonius volgde een andere methode.

[...]

Home | Christiaan Huygens | XI | Meetkunde-problemen (top)

5. Een gegeven driehoek middendoor snijden, vanuit een gegeven punt op een zijde. Stel BC = a; DC = b; AC = c; EC = x. Aangezien dus driehoek EDC de helft moet zijn van driehoek ABC, zal gelden:
vermenigv.	{	DC b 2 EC 2 x		BC a AC c
		————		———
		2 x b	=	a c
		x	=	a c 2 b
Dan geldt dus: b staat tot a, als ½ c tot x.
[ Toelichting: D is gegeven punt, E wordt gezocht. De eerste gelijkheid volgt uit: - de oppervlakte van een driehoek is: halve hoogte maal basis, - voor driehoeken met een gelijke hoek is de hoogte evenredig met de schuine zijde aan die hoek, - dus is de oppervlakte evenredig met: basis maal die schuine zijde. Constructie: Om nu E te vinden: trek BE evenwijdig DF, als F het midden van AC is. ]

7. Een gegeven driehoek middendoor snijden met een lijn die evenwijdig is aan één van de zijden. Stel AC = a; BC = b; EC = x.
a —— b ——	x	/	bx a
			2x
	ab	=	2bxx a
	aa	=	2xx
	aa 2	=	xx
√	aa 2	=	x
Toelichting: In de 2e regel zien we de 'regel van drie': a : b = x : ? Met de uitkomst ? = bx/a, ofwel DC. [ Vermenigvuldiging met 2x levert ab, want (zie de toelichting bij probleem 5) de oppervlakten van driehoeken met een gelijke hoek verhouden zich als het product van de zijden aan die hoek. Constructie: twee kwart-cirkels op AC, Pythagoras geeft x. ]

Meetkunde-problemen, 1645

III.

IV.