Home | Chr. Huygens | < Oeuvres VI >

1655-56 , 1658-59 , 1660 , 1668 , 1673


Vertaling van de

Briefwisseling met John Wallis


[ 251 ]

No 1659.

J. Wallis aan Christiaan Huygens.

10 september 1668.*)
Oxonij, Augusti 31. 1668.  

  De brenger van deze brief (weledele heer), de heer Theodorus Ryckius 1) van Gelderland (die hier een paar maanden verbleef, om te studeren), die nu

  [ *)  Op de originele brief staat links boven: "Rx 31 Oct.", de datum van ontvangst.]
  1)  Dirck de Rycke (Arnhem 1640 - Leiden 1690) studeerde in Leiden, werd rector van de Latijnse school te Kampen, ging in 1667 op reis. In 1671 vestigde hij zich in den Haag, in 1672 werd hij benoemd tot professor geschiedenis en welsprekendheid aan de Leidse universiteit.

[ 252 ]

regelrecht naar Frankrijk gaat oversteken 2), heeft mij verzocht, als ik soms brieven had die naar Parijs moesten worden gezonden, hem als brenger te nemen. Dit handvat heb ik aangegrepen om u aan te spreken, opdat niet de vroeger op gelukkige wijze begonnen vriendschap (wat ik niet wilde laten gebeuren) verloren zou gaan door lange ontwenning.

  Nu drie jaar geleden 3) was hier aanwezig uw beroemde vader, die mij zorgvuldig opspoorde, zeer vriendelijk bezocht, en vereerde met een elegant Epigram 4), wat ik te danken heb aan de vriendschap met u. (Ik was verheugd hem nog in leven te zien en op die leeftijd opgewekt en gezond.)  En nu zeer onlangs, door hem per brief aanbevolen, is uw neef Maurits Wilhelm 5) door mij ontvangen, zo vriendelijk als ik kon; en wat hij met zich

  2)  Deze brief werd pas 31 oktober 1668 aan Chr. Huygens gegeven. Zie brief No. 1671.
  3)  Vader Constantijn Huygens was toen op ambassade naar Engeland gestuurd. [Hij had op 1 juli 1668 een brief aan Wallis geschreven, met zijn boek De zee-straet, 1667.]
  4)  We hebben deze epigrammen gevonden in 'Poemata Latina' in de Koninklijke Akademie van Wetenschappen te Amsterdam [KNAW.  Ed. Worp, Gedichten, VII (1897), p. 63, 64].
[ C. R. Joby, 'A Dutchman Abroad', The Seventeenth Century, 28 (2013) 187-206.]
Geef aan heer Wallis een groet van 't Bataafse geslacht,
  aan studie verslaafd, dat van Zuilichem.
...
  5)  Maurits le Leu de Wilhelm, zoon van David le Leu de Wilhelm en Constantia Huygens, werd in 1641 in Den Haag geboren. Hij studeerde in Leiden en ging later op reis. Zie brief No. 1139, n.10.

[ 253 ]

meebracht aan Werken van uw Vader, bestemd voor de Bodleian Library, hebben we daar ingebracht, om tot sieraad te zijn.

  Hij heeft bekendgemaakt (ik kon het tenminste niet laten naar onze Huygens te vragen) dat u nog in Parijs verblijft; ik geloof dat u er ook zult blijven. Wat ik wel liever anders zou willen, als ik niet zou denken dat het zo overeenkomt met uw belangen. Ik had in elk geval liever gewild dat u een woonplaats had gekozen hetzij bij uw landgenoten, hetzij (als u naar het buitenland wilde gaan) bij ons, even rijk aan kennis; om onze Royal Society, waarvan u een voortreffelijk lid bent, verder tot hulp te zijn, en tot sieraad.

  Om enige dingen over onze gemeenschappelijke studies toe te voegen: ik heb onlangs gezien uw Aanmerkingen op de Kwadraturen van James Gregory 6), in het Journal des Sçavans geplaatst; en wat hij antwoordt 7), geplaatst in de Philosophical Transactions van de onzen.

  En ik zou wel liever willen dat de naam van Huygens er niet bij stond. Want (behalve dat bij propositie 10 het voorbeeld niet geschikt was; en dat bij propositie 7 de breuk (mac − mbc) / (ad − bd) niet was herleid tot de kleinste termen, wat van minder gewicht is, en de hoofdzaak niet raakt) ik zie niet wat eraan hapert. Want, voorzover ik kan oordelen, de 11e propositie die u bestrijdt is naar behoren bewezen; namelijk dat de daar beschreven convergente reeks niet Analytisch is samengesteld (in de zin waarin hij dit begrepen wil hebben).

En wat u uit propositie 7 hierbij sleept, doet de zaak niet af; wat immers aan een bijzonder geval was aangepast, had niet tegen de bedoeling van de schrijver ergens anders bijgesleept moeten worden; en het past hier niet. En wat anderen vroeger (onder wie ook u), met verschillende methoden om getallen te benaderen, voor de kwadratuur van de cirkel hebben bedacht, neemt niet weg dat ook deze van hem welkom is, inderdaad scherpzinnig en nieuw. Vooral aangezien deze methode ook zo is gemaakt, dat ze ook de Ellips en de Hyperbool op voet van gelijkheid beschouwt met de Cirkel; en wel op een mooie manier.

  Dat de afmeting van de Hyperbool verbonden is met de theorie van Logaritmen (wat verschillende mensen op verschillende manieren hebben laten zien): ik erken dat de zaak niet volkomen nieuw is. Niet alleen omdat u misschien dingen hebt gevonden die niet ongelijk zijn aan deze (wat hij naar ik geloof, naast mij ook, niet wist), maar omdat ik het na de uitgave van het Opus Geometricum 8) van Gregorius van St. Vincent [<] voor algemeen bekend houd. (Zie desgewenst onze Commercium Epistolicum 9), brieven 37, 39, 40.)

  Maar hij stelt het ook niet, geloof ik, als iets volkomen nieuws voor (zodat hij daarom te beschuldigen zou zijn), maar hij legt op zijn manier iets uit dat op een andere manier bekend is. Doch ik wil niet dat u meent, dat ik dit daarom zeg alsof ik u dit afneem om hem te begunstigen (hij is mij in elk geval onbekend, evenals aan u, geloof ik; ik herinner me niet hem ooit te hebben gezien, of gesproken, of

  6)  Zie brief No. 1647. ['Vera Circuli et Hyperboles Quadratura', J. des Sç. 2 juli 1668, p. 52-56.]
  7)  Zie brief No. 1653. ['Mr. Gregories answer to the animadversions of Mr. Hugenius', Phil. Trans. Vol. 3, Numb. 37 (July 13, 1668), p. 732-735.]
  8)  Zie brief No. 25, n.6.     9)  Zie brief No. 497, n.3.

[ 254 ]

iets met hem te doen gehad te hebben; zover is het er van af dat ik het aan hem verschuldigd zou zijn, hem gunstiger genegen te zijn dan u, door oude vriendschap bekend); maar, zoals bij een vriend, spreek ik vrijmoedig mijn mening uit. En dit doe ik voornamelijk daarom (de zaak zelf is immers van gering belang), aangezien ik nu na enige ondervindingen weet, hoe van een weinig betekenend begin gemakkelijk wordt overgegaan op twist en afgunst; wat ik hier niet gebeurd wil hebben; of als het noodzakelijk is, wil ik niet dat de naam Huygens in stukken wordt getrokken.

  Iets anders dat ik besloten heb te vermelden is het volgende. De Regel die u levert*) over het meten van een hyperbolisch oppervlak met behulp van Logaritmen, is dezelfde als onder anderen onze Barrow 10) allang had geleverd 11). Aangezien ik daarvan een afschrift heb zal ik niet weigeren het hier (met alleen de taal veranderd van Engels naar Latijn) woordelijk over te schrijven.

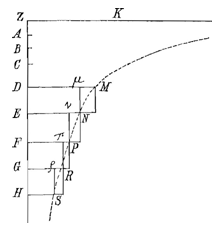hyperbool, met stapjes   Als de asymptoten ZH en ZK van een hyperbool onder een rechte hoek samenkomen, wordt gesteld dat ZA, ZB, ZC, ZD enz. continu evenredig zijn, bijvoorbeeld met de verhouding van tot β. En als de rechten DM, EN, FP, enz. evenwijdig aan ZK zijn getrokken, en de rechthoeken EM en Eμ, FN en Fν, enz. voltooid; dan zullen zowel alle omgeschreven rechthoeken EM, FN, GP, enz. onderling gelijk zijn, als alle ingeschreven rechthoeken Eμ, Fν, Gπ, enz.
En daarom zal EM zoveel keer genomen als er (DE, EF, enz.) delen op DH zijn, groter zijn dan het hyperbolische oppervlak DHSM. En Eμ zoveel keer genomen zal kleiner zijn dan dit oppervlak. Nu is het aantal van die delen op DH gelijk aan het aantal delen op ZH verminderd met het aantal delen op ZD (dat is de logaritme van die ZH min de logaritme van die ZD, welk verschil ik noem L.

  En aangezien  DE = ZE − ZD = β/α ZD − ZD = (β − α)/α ZD,  geldt:
rechthoekje EM = (β − α)/α ZD × DM.
En dus zal  L × (β − α)/α ZD × DM  groter zijn dan oppervlak DHSM.

  [ *)  Le Journal des Sçavans, 2 juli 1668 (zie n.6), p. 56.  Zie ook T. 14, p. 434.]
  10)  Isaac Barrow (1630-1677) zoon van een 'linen draper', werd in 1649 Fellow of Trinity College te Cambridge, ging in 1655 op reis. In 1659 professor in het Grieks te Cambridge, 1662 in de meetkunde aan Gresham College en daarna Lucasian professor, in 1669 opgevolgd door Newton. In 1672 Master of Trinity, waar hij de befaamde bibliotheek liet bouwen. Hij was wiskundige, linguist, theoloog, befaamd prediker over geschilpunten, bescheiden en gewetensvol.
  11)  Wallis blijkt het uit een manuscript te hebben; Barrow's werken verschenen pas later in druk.

[ 255 ]

Evenzo:  EN = α/β DM.  En daarom:
DE × EN = (β − α)/α ZD × α/β DM = (β − α)/β ZD × DM.
En dus zal  L × (β − α)/β ZD × DM  kleiner zijn dan oppervlak DHSM.
  Tot zover hij.
  Dat dit gelijk is aan uw Regel behoef ik niet te vermelden. Immers, als de rechthoeken DM of Dμ zo klein worden voorgesteld, dat het verschil tussen de ingeschreven en de omgeschreven rechthoek, en van elk met het tussenliggende hyperbolische oppervlak, kan worden verwaarloosd, zegt hij: als L (het verschil tussen de logaritmen van de rechten ZD en ZH, of van de hiermee evenredige HS en DM) wordt vermenigvuldigd met EM (die heel kleine rechthoek, of oppervlakte) zal die oppervlakte DHSM worden verkregen. En u zegt: als de logaritme van die L wordt opgeteld bij de logaritme van die EM, zal de logaritme van dat oppervlak DHSM worden verkregen. Wat op hetzelfde neerkomt.
  Maar tot zover hierover.

  Wat mij betreft, ik verbaas me erover wat uw Fransen zich in het hoofd gehaald hebben, dat ze bij elke gegeven aanleiding (of niet gegeven) het op mij gemunt hebben. Wat ik werkelijk tegen hen misdaan heb, weet ik niet; behalve misschien dat ik enige malen door hen voorgelegde Problemen 12) heb opgelost 13). Hoe slecht ik vroeger door hen behandeld ben, weet u voor een deel [<]; en ik herhaal het niet. Wat heeft gemaakt, dat ik me om zo te zeggen vroom ervan heb onthouden, met hen iets van doen te hebben (hoewel enige malen ertoe geprikkeld), met wie iets niet anders dan met verwijten te behandelen was. Wapens van deze soort bevallen mij immers niet.

Na die tijd is het Sorbière (hoewel hij niet ontkent dat hij door mij welwillend ontvangen is), die zijn 'Reis naar Engeland' 14) niet anders (en nogal achteloos) kan schrijven, zonder ook mij even te bespreken. En daar hij niets had dat hij als verkeerd kon aanrekenen, heeft hij tenminste dit voorgesteld als lachwekkend (en zelfs op nogal belachelijke wijze) dat ik volgens onze gewoonte een muts droeg; en dat ik een Academicus was, niet een Hoveling. Maar deze dingen zijn van weinig betekenis.

  Onlangs is mij gebracht een boek van Leotaud 15), dat hij Cyclomathia 16) noemt

  12)  Problemen van Fermat (getallenthorie) en van Pascal (cycloïde). Zie de brieven No. 512 en 690.
  13)  Zie Commercium epistolicum [1658] (No. 497, n.3) en Tractatus duo [1659] (No. 690, n.3).
  14)  Over Sorbiere, Relation d'un voyage en Angleterre, Par. 1664 en de Engelse vertaling [Sprat, Observations, 1665, p. 216 (Fr. p. 100);  A voyage to England, 1709, 2e ex.], zie brief No. 1234, n.9. In de vertaling, p. 41:
muts
Student in Oxford
(Chr. Huygens, 1661)
The Doctor has less in him of the Gallant Man than Mr. Hobbs, and if you should see him with his University Cap on his Head, as if he had a Portefeuille on, covered with Black Cloth, and sewed to his Calot, you would be as much inclined to laugh at this diverting Sight, as etc.
[ Dan: "Wallis ... one of the greatest Mathematicians in the World ...]
  15)  Zie over Vincent Leotaud brief No. 175, n.1.
  16)  Cyclomathia seu multiplex circuli contemplatio tribus libris comprehensa, in I quadraturae Examen confirmatur ac promovetur. II. Angulae contingentiae natura exponitur. III. Quadratrices facultates inauditae proferuntur, Lugd. 1663.  [Zie voor Wallis: p. 166, 171 .. 207 .. 234.]

[ 256 ]

(maar enige tijd geleden geschreven), die als hij klaar is met het weerleggen van zijn Aynscom 17), om het boek aan te vullen, mijn verhandeling De angulo contactus 18) aanvalt, vrij uitgebreid, maar ook vrij onbetekenend en er is weinig dat wiskundig weerlegd moet worden. Maar gelukkig, ik zou geen ander dan u als beoordelaar wensen. Ik heb hem onlangs geantwoord in een brief aan hem persoonlijk; ik weet niet of hij een openbaar antwoord verdient.
Tenslotte Dulaurens 19), als hij zich druk maakt om zijn Specimina 20) te tonen; daaraan heeft hij, om de optocht te versieren, een Aanhangsel toegevoegd; waarin hij mij als bedenker verzint van een of ander minder belangrijk probleem, aan alle Wiskundigen van Europa voorgelegd; om, als hij dit opgelost heeft, over mij te triomferen. En nu ik me beklaagd heb dat dit mij onrecht aandeed 21), vervalt hij woedend in een nieuw schimpschrift 22) tegen mij, vol verwijten; en hij zal me niet met rust laten als ik niet een weerlegging van zijn boek wil schrijven. Ik vind het echter geen weerlegging waard 23). Waarvoor het bij de zijnen kan worden gehouden, weet ik niet. Maar in elk geval, óf ik vergis me zeer, of hij is niet iemand van wie we in de Wiskunde uitnemende dingen moeten verwachten.
Ik heb geen plezier in zulke woordenwisselingen, en ik meen dat ik mijn tijd beter kan besteden. Als zij het echter noodzakelijk maken dat ik ter verdediging van mezelf, zo dikwijls uitgedaagd, moet antwoorden, moeten ze het mij niet kwalijk nemen als ik een jongeman behandel op een manier die hij verdient. Ze moeten echter niet denken dat anderen gekrenkt gaan worden, die over mij en de mijnen een juistere mening hebben; op grond van brutaliteit van enkelen oordeel ik namelijk niet over allen. U echter (weledele heer) als u naar mij luistert: zorg ervoor (zoveel als u kunt) dat kiemen van woordenwisselingen zo mogelijk worden geweerd; in elk geval opdat niet tussen onze Royal Society en die bij u, ongemerkt iets van een schadelijke wedijver ontstaat,
  17)  Zie over Fr. X. Aynscom, Expositio ac Deductio Geometrica [1656]: brief No. 145, n.6.
  18)  J. Wallis, De Angulo contactus et Semicirculi Tractatus, Oxon. 1656.
  19)  De briefwisseling van Fr. Dulaurens met Chr. Huygens wordt later gepubliceerd [1669, en een brief aan aan Colbert, 1669]. Hij is verder onbekend [zie Dagboek Parijs: "Du Laurent", 2 dec. 1660 en 10, 11 (ingewikkelde uitvindingen), 14, 16, 24 dec. (dwaze vondsten).]
  20)  Specimina Mathematica duobus Libris comprehensa. ... de genuinis Matheseos principiis ... de Methodo Compositionis atque Resolutionis, Par. 1667.  [Eerder had hij gepubliceerd: Solutiones aliquot quaestionum ... Opus metaphysicum, Den Haag, 1663.]
  21)  Zie Philos. Trans., Numb. 34, van 13 april 1668 [p. 654: probleem in Commercium (1658), p. 171, van Jean de Montfert;  zie Wren, Parentalia (1750), p. 244 e.v. ("A fictitious name for Mons. Pascal"); Oeuvres de Blaise Pascal VIII (1914), p. 136, 139].
  22)  Responsio Francisci Du Laurens ad epistolam D. Wallisii ad Cl. V. Oldenburgium scriptum (Phil. Trans. No. 38, p. 744).
  23)  Toch had Wallis geantwoord in Phil. Trans. Numb. 38, 17 aug. 1688 [brief aan Oldenburg: July 2] ... Numb. 39, 21 sept. 1668 [p. 775; brief: July 18] ... Numb. 41, 16 nov. 1668 [p. 825, vervolg].
[ Zie: Jacqueline Stedall, 'John Wallis and the French', Hist. Math. 39 (2012) 265-279.]

[ 257 ]

maar opdat die veeleer op vriendschappelijke wijze door gezamenlijke inspanningen de ware Filosofie bevordert, en dat de ene de andere niet tekort doet, of een gelegenheid aangrijpt om te pochen.
Tenslotte, het ga u goed, veel geluk, en blijf genegen,

Tui amantissimum et observantissimum  
Joh: Wallis.      

Clarissimo Eruditissimoque Viro,
D. Christiano Hugenio de Zulichem,
        Parisijs.



[ 278 ]

No 1671.

Christiaan Huygens aan J. Wallis.

Aanhangsel bij No. 1670
13 november 1668.

Celeberrimo Doctissimoque Viro
Doctori Jo. Wallisio, Chr. Hugenius
S. P.

  Uw brief van de laatste dag van augustus is uiteindelijk pas op de laatste dag van oktober naar mij gebracht door Doctor Ryckius, van wie ik, daar ik niet had gelet op de erop geschreven datum, en het lezen ervan had uitgesteld tot hij was weggegaan, de oorzaak van de zo lange vertraging niet te weten ben gekomen, al herinner ik me dat hij enige verontschuldiging heeft aangevoerd; en hij is later niet naar mij teruggekomen, al had hij iets anders beloofd.
Dus vraag ik u, vriendelijke heer, wegens het zo late antwoord niet in ernst een verdenking over mij te hebben; ik zou hoe dan ook een straf verdienen te ondergaan, als ik een brief die zo vriendelijk en zeer aangenaam geschreven is, met vermelding van het begin van uw vriendschap zowel met mijn vader als met mij, zo lang zou hebben veronachtzaamd. Zeker, het is nu wel bijna drie jaar geleden 1) dat de briefwisseling
  1)  De laatste brief van Chr. Huygens aan R. Moray, No. 1530, was van april 1666; die van R. Moray van 24 mei 1666, No. 1540, was onbeantwoord gebleven.

[ 279 ]

niet alleen met u, maar ook met de overige geleerde heren van de Royal Society, door mijn schuld, zoals het gezien kan worden, onderbroken is gebleven, en als zij daarover klagen: het is een beklag dat zij gemeen hebben met alle andere vrienden van mij uit andere streken. Maar ik ben stellig niet anders dan door dwingende noodzaak, en hoezeer ook tegen wil en dank, ertoe gebracht zo te handelen, aangezien ik had gemerkt dat ik niet langer was opgewassen tegen de van dag tot dag groeiende last van het schrijven van brieven, tenzij ik, er genoegen mee nemend dit ene te doen, de overige studies zou opgeven.
Doch ik zou niet willen dat ze denken dat daarom iets van de oude genegenheid is afgegaan, of dat ik vergeten ben met welke buitengewone vriendelijkheid en welwillendheid u en de uwen mij als nieuw aangekomene 2) hebben ontvangen en met allerlei bewezen diensten aan u gebonden; ja zelfs heb ik herhaaldelijk die heel genoeglijke tijd weer in herinnering, en de gezichten en tegelijk de namen van de uitstekende heren, met wie ik zozeer bekend mocht worden. En het voortreffelijke plan voor een Royal Society heb ik vanaf die tijd, meer dan wie ook, werkelijk toegejuicht; toen ik onlangs de geschiedenis 3) ervan doorlas, in een zeer elegante stijl geschreven, gaf me dit ook veel genoegen. Maar als het lot had beschikt, dat ik mijn leven veeleer bij u, dan hier zou leiden, zou misschien mijn werk voor u nuttiger zijn geweest, wens en uitvoering zou niet gemakkelijker kunnen zijn geweest; en daarom moet u het niet teveel betreuren, dat dit gebeurd is zoals het is uitgevallen.
Wat meer is, sinds ik hier gekomen ben, heb ik er niet van afgezien naar vermogen te zorgen voor wat u aanbeveelt; namelijk dat er niet iets van afgunst en tegenwerking ontstaat uit wederzijdse wedijver tussen deze Academie van ons en de uwe, en ook in de toekomst zal ik er moeite voor blijven doen. En er is bij de onzen zeker niemand, die jegens u anders gezind is dan redelijk is, of die u niet heel hoog schat, zodat u zelf daarom misnoegd zou worden, als u in aanmerking neemt dat zulke Fransen als Leotaud, Sorbiere of Dulaurens niet op gelijk niveau met u staan. Van wie er één zoals u weet een straf heeft ondergaan wegens brutaliteit 4) en allen, voorzover ze u ten onrechte aanvallen, verontwaardiging wekken bij goede mensen. En wat betreft degene die ik het laatst heb genoemd, daar hij in geleerdheid en kennis van de wiskunde heel ver voor u onderdoet, maar misschien in ervaring met het ophopen van beschimpingen bij twisten helemaal niet de minste is, betreur ik het dat met hem een geschil is ontstaan; en nu geef ik ook de raad, zo spoedig mogelijk de strijd op te geven als zijnde u onwaardig, aangezien hij de meer verstandige adviezen verwerpt en zijn drift niet kan beheersen.
Overigens, zoals u bij mij op vriendschappelijke voet klaagt over onrecht dat u is aangedaan, zal ik op mijn beurt bij u mogen spreken over het mijne.

  Of ik al dan niet terecht de bewijzen van James Gregory heb afgekeurd 5) zal ik nu niet vragen, daar u uit hetgene, dat ik nu heel kort geleden geantwoord heb 6), zult begrijpen over welke plaats die controverse gaat. Ik geloofde stellig dat hij door die eerste bespreking van mij zich volstrekt niet beledigd zou gaan voelen, want ik heb ook niet zonder lof over de hoofdzaak van het werk gesproken 7), en ik nam aan dat het

  2)  Chr. Huygens was in de lente van 1661 in Londen [>] en daarna, met zijn vader, van 10 juni tot 18 sept. 1663 [>]. Hij werd als lid van de Royal Society toegelaten op 17 juni 1663 (oude stijl).
  3)  Zie brief No. 1114, n.4 [Thomas Sprat, The History of the Royal-Society of London, 1667].
  4)  Sorbiere. Zie brieven No. 1242 en 1247.  [No. 1238, oordeel Huygens (juni 1664): "overhaast oordeel ... vaak niet zo goed op de hoogte".  Boekverbod: Arrest du Conseil d'Estat, 9 juli 1664.]
  5)  Zie brieven No. 1647 en 1648.
  6)  Zie brief No. 1669 [Journal des Sçavans, 12 nov. 1668, p. 109].
  7)  Zie de inleiding van het artikel in J. des Sç. [2 juli 1668, ed. Amst.], p. 361 ...

[ 280 ]

geoorloofd was, dingen die niet zo duidelijk bewezen waren te onderzoeken. Dat ik evenwel had toegevoegd dat ik vroeger over de Afmeting van de Cirkel iets heb uitgegeven dat nauwkeuriger was het zijne, dat heb ik zowel naar waarheid gezegd als bescheiden, meen ik, met verzwijging namelijk van wat ik terecht had kunnen tegenwerpen; dat hij de belangrijkste theorema's die hierop betrekking hebben uit mijn boekje heeft genomen, dat hij immers ontegenzeglijk dezelfde heeft bewezen en slechts op een andere manier, en dit zonder enige vermelding van mij. Maar ook had hij mij met zijn vrij gematigde en beleefde antwoord 8) ervan overtuigd, dat hij die eerste opmerkingen van mij niet te zwaar had opgenomen.
[ 7)  vervolg.]  Deze inleiding leek op het eerste gezicht afkomstig uit de pen van de uitgever van het Journal. Omdat uit deze brief aan Wallis blijkt dat het artikel daarentegen geheel door Chr. Huygens is geschreven volgt het hier, tot aan het geciteerde in brief No. 1647, n.2.
  Omdat het Probleem van de Kwadratuur van de Cirkel vanwege zijn moeilijkheid altijd veelbesproken is geweest, hebben de meest scherpzinnige Meetkundigen van alle tijden hun best gedaan daarvan de oplossing te vinden, die bestaat uit het tonen van een manier om een door rechte lijnen begrensde Figuur te maken, gelijk aan een gegeven Cirkel. Maar hoewel ze er zo dicht toe zijn genaderd, dat men verzekerd is dat men zich slechts met de dikte van een haar zou verrekenen in de Kwadratuur van een Cirkel zo groot als de hele Aarde; niettemin heeft nog niemand de laatste precisie kunnen bereiken die de Meetkunde vraagt.
  De schrijver van dit Boek [1667] behandelt dit onderwerp op een nieuwe manier. Ten eerste wil hij laten zien dat de verhouding van de Cirkel tot het Vierkant van de diameter niet analytisch was, zoals hij het noemt, het is tevergeefs dat men deze tracht uit te leggen met gebruikelijke termen van de Meetkunde. Vervolgens leert hij een korte en gemakkelijke methode om de werkelijke afmeting van de Cirkel zo dicht te benaderen als men wil, en hij zegt dat dit het enige is dat men in deze materie kan verlangen. Ook toont hij met dezelfde methode een middel om de Kwadratuur van de Hyperbool te vinden; daarvan het oppervlak te bepalen en de logaritme van een of ander getal te berekenen, en het getal bij welke logaritme dan ook.
  De belangstelling van allen die enige kennis van de Wiskunde hebben voor de oplossing van het probleem van de Kwadratuur van de Cirkel, maakte hen nieuwsgierig of dit Boek voldoet aan de verwachting die de titel wekt. Zodra het begon te verschijnen, hebben de beroemdste Meetkundigen van Engeland het bestudeerd en ze hebben er een heel gunstig oordeel over gegeven. En men kan zeker in het algemeen zeggen dat dit Boek met veel verstand geschreven is, en dat het verscheidene heel scherpzinnige bewijzen bevat. Maar ze hebben niets in het bijzonder gezegd over de meest opmerkelijk propositie, waarin de Schrijver beweert te hebben bewezen dat het onmogelijk is de Kwadratuur van de Cirkel analytisch te vinden.
In Frankrijk heeft men dit Boek ook bestudeerd, in de Vergadering die gehouden wordt in de Bibliotheek van de Koning. En omdat voor wie van Meetkunde houdt niets ongewoner is dan deze materie, heb ik gemeend dat het passend was hier verslag te doen van wat men daat in overweging heeft genomen.
  8)  Zie brief No. 1653. [Phil. Trans. No. 37, 13 juli 1668 (o.st.), p. 732-735.]
[ Christoph J. Scriba, 'Gregory's converging double sequence', Hist. Math., 10-3 (1983) 274-285.]

[ 281 ]

Sindsdien echter, toen hij dit argument grondiger had bekeken, en iets beters had gevonden dan wat aanvankelijk was geleverd, door het succes strijdlustiger gemaakt naar het schijnt en niet verwachtend wat ik tegen hem zou inbrengen, vaart de man uit met een heel onaangenaam geschrift 9) tegen mij die niet iets dergelijks vreesde, en voorwendend dat hij wordt beschuldigd van diefstal verwijt hij me openlijk een leugen; de werkjes 10) die ik vele jaren geleden heb uitgegeven kleineert hij zoveel hij kan, terwijl hij toch, zoals ik gezegd heb, een belangrijk deel van het zijne daaraan ontleend heeft; tenslotte: waar mogelijk smaalt hij, haalt hij neer, beledigt hij. En ook heb ik het lastiger gevonden dat hij aan de titel van het boekje 9) laat voorafgaan dat hij lid van de Royal Society is, en aangezien deze vol verstandige heren is, mij ook niet kwaadgezind voorzover ik weet, had ze zeker die verblinde overmoed van mijn tegenstander in toom moeten houden. Maar ook nu zouden ze, als ze tegen hem enige rechtsmacht hebben, hem moeten dwingen het in te trekken, opdat het voor mij niet nodig is mijn mening ook openlijk te verdedigen, zoals die openlijk is aangevallen. Hoezeer ik immers tegen wil en dank tot zulke twisten overga, weten zij die mij kennen.
Wat echter de beschuldiging betreft, waarmee hij beweert dat ik naar de uwen niet de Regel 11) heb gestuurd, gebaseerd op de afmeting van de hyperbool, om de zwaarte van de Lucht te vinden bij gegeven hoogten vanaf de grond, de illustere ridder Moray zal die, als hij mijn brieven heeft bewaard, daarin ergens terugvinden, en ik zou ook als het nodig was zijn antwoord 12) kunnen leveren, waarin hij te kennen gegeven heeft dat die regel uw Meetkundigen wel beviel; maar het valt te geloven dat Gragory niet zeer zorgvuldig de waarheid van de zaak heeft opgezocht. Overigens, toen dit krenkende boekje werd aangevoerd, was mijn antwoord 13), dat met deze brief naar u wordt gebracht, al gedrukt; en al is het nu gematigd, en passend bij het eerste en niet bij het tweede geschrift van Gregory, toch heb ik niet willen tegenhouden dat het in het licht zou verschijnen, daar allen zullen erkennen dat mij een des te groter onrecht is aangedaan, naarmate ze zien dat het langer heeft geduurd. En hierover al wel teveel woorden, maar u zult me de terechte verontwaardiging vergeven, hoop ik.

  Dat u erop wijst, dat door uw Barrow dezelfde afmeting van de hyperbool met logaritmen is gevonden als de mijne: denkt u vooral niet dat dit voor mij niet zo aangenaam is; als hij immers niet wist dat ik het had gevonden, evenals ik het niet van hem wist, komt aan elk van ons beiden geheel de lof toe.

  Maar als we de werkelijke toedracht willen erkennen: een groot deel ervan komt toe aan Gregorius van St. Vincent, die als eerste een vergelijking van hyperbolische oppervlakken heeft opgesteld; en dit overwegend heb ik er niet voor gezorgd die al eerder gevonden regel aan te bieden, aangezien ik tot nu toe ook veel belangrijker dingen heb geleverd.

Het ga u goed, weledele heer en wees mij genegen zoals ik u genegen ben.

  Dabam Parisijs 13 Novembris. 1668.

  9)  Zie het stuk No. 1684. [Exercitationes Geometricae, Lond. 1668, Praefatio, Appendicula.]
  10)  Theoremata de Quadratura hyperboles, ellipsis et circuli [1651, Ned.] (brief No. 95, n.1) en De Circuli magnitudine inventa [1654, Ned.] (No. 191, n.1).
  11)  Zie brief No. 1046, 18 aug. 1662, en Aanhangsel II, No. 1048.
  12)  Zie brief No. 1055 [1 sept. 1662].       13)  Zie brief No. 1669.



[ 296 ]

No 1676.

J. Wallis aan Christiaan Huygens.

Aanhangsel bij No. 1675
23 november 1668.

Oxoniae Novembris 13. 1668.  
    Nobilissime Vir,

  Uw zeer vriendelijke, en mij zeer welkome brief, afgegeven te Parijs op de 13e november van uw stijl, heb ik hier ontvangen op de 12e, volgens onze stijl. Waarom nu mijn brief 1) zo laat aan u is geleverd, weet ik niet. Ik had hem in elk geval op dezelfde dag geschreven als waarop hij gedateerd was; en op die dag (als ik me herinner) is de heer Ryckius van hier weggegaan; door wie hij kort daarna naar Londen (zoals hij besloten had) werd gebracht; hij had gezegd dat hij binnen acht dagen vandaar weg zou gaan, rechtsreeks naar Frankrijk zou oversteken, en tenminste voor het eind van september bij u in Parijs zou zijn. Maar het kan heel goed zijn (wat reizigers gewoonlijk overkomt) dat hij een minder vlotte reis heeft

  1)  Brief No. 1659.

[ 297 ]

gehad dan hij had gehoopt. Doch het is niet van veel belang; aangezien daarin niets stond dat veel haast vereiste.

  Wat James Gregory betreft: ik weifel over wat ik moet zeggen. Daar hij toch zo slecht gebruik heeft gemaakt van eerder betoonde bijval, dat ik niet weet of ik niet spijt zou moeten hebben van wat ik ten gunste van hem had gezegd. Over zijn boekje 2), toen nog maar net uitgegeven, om een mening gevraagd, had ik enige algemene dingen geantwoord; voorzover mogelijk na oppervlakkig inzien, nog zonder onderzoek van bijzonderheden; en ik was er verder niet mee bezig. Waaraan anderen (naar het schijnt) iets anders toevoegden, waarmee de heer Oldenburg de karakterisering vormde die hij heeft uitgegeven 3).

Nadat uw opmerkingen waren uitgegeven 4), en zijn antwoord 5), wist ik nog niet dat wat hij aan zou bieden, daar naar behoren is bewezen, dat de cirkel niet Analytisch (zoals hij het noemt) gekwadrateerd kan worden. Hoewel hij namelijk iets dergelijks in zijn Voorwoord lijkt aan te geven, leek het daar toch onwaar, omdat Het hele bewijs nog niet was herleid tot de Meetkundige wijze van uitdrukken. Wat ik althans zo heb uitgelegd, alsof hij aangaf dat de zaak hem waar leek (zoals het mij ook leek), maar door hem nog niet Meetkundig streng bewezen. Wat heeft gemaakt dat ik schreef 6) wat u in de vorige brief hebt gelezen.

  Doch terstond nadat ik die gestuurd had, werd ik onverhoopt lastig gevallen: hij beweerde dit niet alleen als iets waars, maar als door hem naar behoren bewezen; en hij eiste dat ik hetzij ditzelfde terstond wilde uitspreken, hetzij redenen voor het tegengestelde naar voren zou brengen, waarop hij zou kunnen antwoorden. En aangezien ik het eerste niet kon, heb ik het laatste gedaan; ongeveer in deze zin.

Namelijk (behalve dat hij veel lemma's van te voren had aangenomen die, al zouden ze waar zijn, toch niet zonder meer gepostuleerd moesten worden, maar veeleer bewezen, voordat gezegd moet worden dat het bewijs voltooid is), tenminste de volgende twee waren een belemmering, waardoor ik dat niet kon uitspreken. Te weten, dat het omgekeerde van de tiende Propositie niet bewezen is (toen u hem bijna ditzelfde had tegengeworpen, had hij niets er tegenover gesteld). En dat, al zou dat wel volkomen bewezen zijn, en dat dus (wat Propositie 11 beweert) Een onbepaald genomen sector niet Analytisch is enz., en dus niet elke; hieruit volgt toch niet dat er geen is, en dus ook niet, dat de Cirkel zo niet gekwadrateerd kan worden, omdat het hiervoor niet nodig is dat alle maar dat enige zekere sectoren (zoals hij zegt) Analytisch zouden zijn met het kwadraat van de straal of van de diameter. (Dat dit niet zomaar is tegengeworpen, heb ik met enige voorbeelden laten zien.)
Het is er zover van verwijderd dat deze twee hem voldoening geven, dat hij op mij niet veel minder boos is dan op u; zowel daar ik me niet terstond voor hem heb uitgesproken,

  2)  Zie brief No. 1605, n.4.
  3)  Zie Phil. Trans. van 16 maart 1668, Numb. 33, over het boek van Gregory:
This tract perused by some very able and judicious mathematicians, and particularly by the lord Viscount Brouncker and the reverend Dr. John Wallis, receiveth the character of being very ingeniously and very mathematically written, etc.
  4)  Zie No. 1647 en 1648.     5)  Zie brief No. 1653.     6)  Zie brief No. 1659.

[ 298 ]

als omdat hij beweert dat het aan mij gelegen heeft, dat hij van de Royal Society nog niet zo'n soort getuigenis heeft gekregen (wat hij heel graag zou willen). En zo hebt u (weledele heer) wat ik over deze zaak heb gedacht. Wat anderen denken, hoor ik nog niet. Maar ik weet ook nog niet wat het is dat u antwoordt 7). Al meen ik namelijk dat de heer Oldenburg het heeft ontvangen, toch hebben we het hier nog niet ontvangen.

  Wat het overige betreft: wat dat is, waarvan u zegt het vroeger aan ridder Moray te hebben geschreven 8), ik herinner me niet het te hebben gezien, zodat er niets is dat ik erover kan zeggen. Toch twijfel ik er niet aan dat hij voor u voldoende onpartijdig zal zijn.

En dat u zegt dat het voor u niet onaangenaam is dat aan onze Barrow datzelfde bekend was wat u noemt: En dat u (wat de hoofdzaak betreft) erkent dat de vergelijking van hyperbolische oppervlakken met Logaritmen oorspronkelijk aan Gregorius van St. Vincent moet worden toegeschreven: Dat doet u geheel zoals het een oprecht iemand betaamt.
Doch wat meer kwetsend tegen u is gezegd, denkt u vooral niet dat het mij genoegen deed; ik heb ook zo goed als hetzelfde ondervonden, niet alleen in persoonlijke brieven aan mij, maar ook in het voorwoord van het laatste boekje 9); dat u (geloof ik) eerder had gezien dan ik. Waarin Gregory, nadat hij op zeer onaangename wijze genoeg geklaagd heeft, een of ander fragment, geplukt uit een of andere brief van mij 10) aan een ander 11) geschreven, onvolledig citeert (met weglating van wat het voornaamste was) en niet voldoende getrouw. Ik heb namelijk niet (wat hij zegt) tegen zijn Theorie iets tegengeworpen (daar ik die zelf, als ik me niet vergis, vroeger had bewezen, in propositie 190 van Arithmetica Infinitorum) maar tegen het Bewijs. (En ik had wel uitdrukkelijk gezegd dat ik de zaak volstrekt niet verwierp, maar dat ik niet zag, waar ze dan wel bewezen werd.)  Maar ook is het niet zo dat ik aannam (wat hij beweert) dat bewezen is, dat de sector ABIP niet Analytisch is samengesteld, enz.; maar dat deze niet zoals gezegd werd analytisch is samengesteld; dat wil zegen, niet op die manier die hij bij propositie 10 had aangeduid.
Ik heb besloten deze twee te vermelden (met weglating van het overige), opdat u mijn mening niet uit zijn woorden anders opvat dan ze is. Tenslotte zou ik niet willen dat u denkt dat de Royal Society over u een andere mening heeft dan passend is. Het ga u goed, weledele heer, en blijf genegen

Tui studiosissimum  
Johannem Wallis.  

Nobilissimo Eruditissimoque Viro
D. Christiano Hugenio de Zulychem,
        Parisijs.

  7)  Zie brief No. 1669.     8)  Zie brief No. 1671.     9)  Zie stuk No. 1684.
  10)  Zie brief. No. 1672.     11)  De brief was door Wallis aan Brouncker gericht.



[1673]


Home | Christiaan Huygens | T. VI | John Wallis (top) | vervolg