| [ 331 ] | [ v ] |
|
Christiaan Huygens à John Wallis.13 juin 1655.La minute et la copie se trouvent à Leiden, coll. Huygens. Sommaire: liber meus. Satelles. Setho Wardo.
Christianus Hugenius S. D. Cum annis ab hinc tribus 1) ni fallor Fr. Schotenius literas tuas mihi legendas misisset, in quibus linearum curvarum novam inventionem proponebas, iterum nunc alteris acceptis quibus ad Circuli quadraturam eas lineas tendere profiteris, has quoque mecum communicandas duxit*), rogans simul ut perpensis ijs non amplius se internuncio uti vellem sed ad te ipsum responsum adornarem; nam se quidem non facile ad mentem contemplationem tuam revocaturum quod priores litterae tuae ad manum non essent, apud amicorum aliquem aut inter chartas delitescentes. Facio itaque Vir Clarissime et quod ille desiderat, et quod illo non admonente tamen facturus eram, cum non parum ad me quoque spectare visa sint quae scribis sepius iterata mei mentione. Ad lineas itaque à te propositas quod attinet, rectè existimas ad Geometricarum numerum eas accenseri posse etiamsi criterium illud nostrum non ferant. atque ego id tantum ostendere volebam non convenire ipsis eam proprietatem quam tribuere velle videbaris, nimirum ut sumptis in tangente ad verticem ab ipso contactus puncto (ita enim tunc intellexeram) partibus aequalibus magnitudinis arbitrariae (postquam jam curva delineata esset) perpendicularis quae tunc erat prima esset partis unius qualium tertia partium 6. quinta 30 &c.°) 1) C'était en décembre 1652. Voir aussi la Lettre No. 144. [ *) Voir p. 328. °) Figure: p. 209.] |
| [ 332 ] | [ v ] |
|
Ejusmodi enim curva nulla est, sicuti nulla quoque est in qua ijsdem quae dixi positis, secunda sit partis 1. quarta 6. sexta 30 &c. Ergo quum pro Geometricis adhuc haberi postules lineas tuas, oportere arbitror ut proprietatem aliquam in singulis designes, per quam puncta quotlibet in ipsis determinari queant. nam mihi nunc tales videntur, ut si per certa quaedam puncta transeant, praeter illa verò nulla definitum locum obtineant. Nam quod aequabiles curvas duci vis, id non videtur sufficere ad exhibendas lineae partes inter bina quaeque puncta interjectas. Sed fortasse haec ego temere, non intellecta satis sententia tua aut proposito. Itaque praestare arbitror ut examini supersedeam donec universam methodum tuam nobis explanes, quae quidem subtilitate eximium promittit. summopere profecto videre desidero qua ratione ad circulum pertineant novae hae Quadratrices. Theoremata mea de Hyperbolae et Ellipsis Quadratura à te lecta esse mihi gratulor; Quae vero anno praeterito de Circuli Magnitudine Inventa edidi una cum constructionibus nonnullorum problematum, ea an ad vos quoque jam pervenerint dubito. In 'exetasi' mea Quadraturae Gregorianae non omnino immerito id reprehendis, quod pagina 36 linea 2 tantummodo duplicatam, aut triplicatam proportionem commemoro aut ulterius multiplicem secundum numeros ab unitate consequentes. quum tamen ut numerus quivis ad alium ita possit esse ratio ad rationem. Attamen quum ad Patris Gregorij mentem non alia quam duplicata altera alterius ratio illic esse debuerit, ut ex prioribus ipsius Theorematis satis constat, fortasse ne quidem triplicatae mentio mihi facienda erat, multoque minus alterius cujusquam. et satis fuisset ostendere non convenire duplicatam. Hanc pro me excusationem adducerem si quam super istis verbis litem antagonista meus moveret. Verum conticuere omnes. Et jam me quoque conticescere tempus est, neque otio tuo abuti diutius. priusquam tamen te dimittam accipe hunc quem apud te depono gryphum quemque eodem hoc tempore alijs multis Viris Egregijs impertio, haud multo post omnibus explicandum. Perspicillum mihi nuper paravi ipse 12 pedum longitudine, quo vix aliud praestantius reperiri existimo quam, quum antehac nemo viderit, quod ego recens observavi. Scribitur autem transpositis literis in hunc modum. ADMOVERE OCVLIS DISTANTIA SIDERA NOSTRIS, VVVVVVVCCCRRHNBQX. a) Doctissimo Collegae tuo Domino Setho Wardo 2), quem ab editis aliquot opusculis 3) nuper novisse coepi si placet haec imperties ut ipsum quoque si quando opus sit testem habeam nemini ante me id visum fuisse, quod literis istis occultatur. Vale. a) Saturno luna sua circunducitur diebus sexdecim, horis quatuor. [Chr. Huygens]. 4) [ Het citaat van Ovidius (Fasti, I, 305) werd al gebruikt door Willebrord Snellius, in De maculis in Sole animadversis ... Batavi dissertatiuncula (1612), p. 1 en door Tommaso Campanella, in Apologia pro Galileo (Francof. 1622), p. 17.] 2) Seth Ward [... 1617 - 1689 ...]. 3) Idea trigonometriae demonstratae [...]. Item praelectio De cometis. Et Inquisitio in Bullialdi Astronomiae philolaicae fundamenta [...] 1653 / 1654. 4) Dans la minute de la Lettre No. 223, on trouve les phrases suivantes, que Chr. Huygens avait taché de convertir en anagramme: In Saturno novilunia recurrunt post dies sexdecim cum sextante. Saturnum sua luna circuit diebus sexdecim cum sextante. Luna bis octonis Saturnia regna diebus lustrat. |
| [ 335 ] | [ v ] |
|
John Wallis à Christiaan Huygens.1 juillet 1655.La lettre se trouve à Leiden, coll. Huygens.
Literas tuas (Eruditissime Vir) Hagae Comitis datas Jun. 13. 1655. st. n. hoc ipso die accepi, et lubenti animo acceptavi. Quae de Curvâ nostrâ habes, non est cur multis ventilem. Geometricam istam esse, ubi intelligas (quod, spero, jam citò fiet) quomodo istuc pervenerim, non fore credo ut dubites. Quaenam autem illa sit aequatio quae singula indifferenter respiciat puncta, id ipsum erat quod Domino Schotenio considerandum proposui, in quo et ipsius opem si vacaret expetivi. Quousque illam disquisitionem ipse perduxeram, aut etiamnum perduxi, brevi spero fiet ut intelligas; tractatus enim aliquot sub prelo jam aliquandiu habui, qui nisi Typographorum morae impedissent diu antehac lucem conspexerant: unde etiam simul intelligas qua ratione ad Circulum pertineant et illa et aliae curvae illic expositae. Nec tantum ad circulum (cujus solius mentio facta est in illa quam ad Dominum Schotenium nuper transmisi chartulâ) sed et ad Ellipsin, Hyperbolam, Parabolam, Paraboloidea omnigena, aliasque figuras curvilieas innumeras quadrandas; sed et ad |
| [ 336 ] | [ v ] |
|
alia quamplurima abstrusiora Matheseos problemata, partim ab alijs antehac excogitata, partim penitus neglecta et a nobis primitus detecta. Cur autem chartulam illam libri prodromum 1) praemiseram, in causa erat quòd audiveram quendam apud nos 2) jactitâsse se circuli quadraturam absolvisse, aliaque miranda praestitisse. Unde facilè conjiciebam fieri posse ut ipsius cogitata aliqua cum nostris coincidant. Et propterea quousque ego rem illam ante complures annos perduxeram viris Mathematicis significandum judicavi, ne deinceps forsan videar, si fortè libellus ejus citius prodiret, ab illo didicisse. Propositionem autem illam Cyclometriam quam nuper ad vos transmisi, (quamque ante aliquot annos excogitatam fuisse et Tu et Dominus Schotenius, inter alios quamplurimos, testes estis,) divulgare solam placuit, sine ullà reliquorum quae a nobis sunt inventa et demonstrata mentione: quoniam si vel hoc unum a nobis olim inventum esse constiterit, non insuper dubitabitur an et ea etiam cognoverim quae nos illò perduxere, et sine quorum cognitione ne hoc quidem excogitâsse potui. Postquam autem hanc nostram Cyclometriam palam professus fueram, et typis concreditam divulgaveram; mihi nunciatum erat Dominum Hobbes nostratem, in ipsius opere quod tunc (sicut et nostrum) sub prelo erat, circuli quadraturam penitus absolvisse, et quidem Geometricè (ut loquuntur) solius regulae et circini beneficio. Ubi autem nunc nunciatum est, quamquam non dubitârim Circuli quadraturam utcunque perficiendam, rem fore possibilem (quam quidem annon et ipse perfecerim judicent Mathematici ubi ea quae scripsi publici juris fient;) tamen ut hoc solâ regulâ et circino perficiatur, quod ille prae se ferebat, rem planè incredibilem et supra omnium Mathematicorum fidem et ego et alij pronunciavimus, non dubij quin alicubi mirè fuerit hallucinatus. Nec quidem secus accidit. Hac enim (uti loquitur ille praepropera malevolorum insultatione monitus), re maturius cum amicis perpensâ illam de quo gloriatus fuerat Circuli quadraturam retractum ibat, et, quaternionibus aliquot quos operae jam ante absolverant laceratis, eorum loco, post secundas curas, alios substituit, aliumque prioris loco tetragonismum: et tandem, cum neque ita res in tuto erat, chartis aliquot tertijs adhuc curis immutatis, ingenuè se fatetur rem neutiquam absolvisse, et quae prius ut apodictica professus erat, jam vult ut tantum problematicè dicta intelligantur. Sed et libelli ipsius prout tunc erat imperfecti editionem properabat, (non exspectatâ vel reliquorum erratorum emendatione, vel sectionis secundae quae deest adjectione,)
1) Il est probable que cette lettre, adressée à van Schooten, n'a guère différé de l'écrit publié peu de jours après sous le titre: Epistola ... D. Guilelmo Oughtredo ... 19 Julii 1655 [Aritmetica infinitorum, Dedicatio]. Wallis y traite entre autres de l'histoire de sa courbe [...]. Il y joignit une lettre: ... Oughtredo ... Postridie Paschatis A. D. 1655 [^]. 2) Thomas Hobbes, mentionné plus loin. |
| [ 337 ] | [ v ] |
|
partim ut amicis id flagitantibus satisfaciat, partim etiam alijs de causis, quas (inquit) dicere non est necessarium: inter quas fieri potest ut haec una sit, ne, si nostra fortè (quam tunc publicè promiseram) Cyclometria prius prodiret, ipsius pseudo-tetragonismo non sit opus; vel ne ille 3) etiam quem Academiarum Vindicem toties appellat (vir doctus et speciatim Matheseos peritissimus, qui, in libello Anglicano cui titulum fecit Vindiciae Academiarum 4) contra nebulonem quendam anonymum Academiarum universim omnium calumniatorem nuper edito, etiam obiter Hobbesij procaciores in Academias item omnes insultus, ipsius Leviathani 5) insertos, lepidè castigaverat,) aliquid ipsi laudis praeriperet. Utut sit, cautionem illam quam adhibui non planè in castum esse deprehendo; quamquam enim libro ipsius jam ante aliquot dies (praeterita septimana) apud nos edito edoctus sim ab ipsius quadratura circuli non opus esse ut formidem, attamen quae istic habet de Parabolastri mensurâ (si paralogismos excipias et 'pseudapodeixeis' quibus passim scatet) pars est eorum quae nos olim methodo nostrâ de Paraboloidibus invenimus, ijsdem principijs nixi quibus et circuli quadraturam investigavi: quorum ope ea quae apud te in 'exetasei' tuâ Cyclometriae Vincentianae occurrunt (quae in nuperis meis ad Dominum Schotenium literis me more meo examinâsse dixeram) vera deprehendi. Quod non ita tamen intellectum velim acsi a nobis haec habuerit, (unde enim habuit, aut an ipse invenerit nescio;) sed eadem utrique, quod rem eandem tractantibus non rarò accidit, obvenere. Quod autem ego obiter monui (in nuperis meis ad Dominum Schotenium) ad paginam 36. lineam 2. tuae 'exetaseôs', leviculum erat, quod ad pleniorem demonstrationis 'akribeian' videbatur deesse, sed quod siquis postulet suppleri posset. Si autem illud addere (uti ais) non esset, ad hominem, necessarium, fateor eo tutius omitti posse. 3) Seth Ward. 4) Vindiciae academiarum ... upon Mr Websters book, 1654 [txt ...]. 5) Leviathan or the Matter, Forme, & Power of a Common-wealth ecclesiasticall and civill ..., Lond. 1651 [...]. |
| [ 338 ] | [ v ] |
| Gryphum tuum quod attinet, ego eum Domino Wardo ubi Domum redierit communicabo; et gratulor tibi observata tua; nam et nos etiam nostrique hic terrarum Mathematici ejusmodi observationibus aliquando vacamus, perspicillis et varij generis et variae longitudinis instructi, putâ pedum 6, 12, 24, 52, lentibus autem nunc solis convexis, nunc concavis et convexis; et quidem numero 2, 3, 5. et non pauca forsan alibi haud observata deteximus. Et Gryphi tui loco liceat mihi tecum alium deponere, quem et posthac si forte opus fuerit deposcam. |
9 1 5 4 9 1 1 12 3 6 6 7
aaaaaaaaa b ccccc dddd eeeeeeeee f h iiiiiiiiiiii lll mmmmmm nnnnnn ooooooo
5 1 11 13 8 17 1
ppppp q rrrrrrrrrrr sssssssssssss tttttttt uuuuuuuuuuuuuuuuu x
|
|
Quae de Circuli magnitudine inventâ anno praeterito edisti, fateor me vidisse quidem (nuper;) at nondum ea vel examinare vacavit, vel quidem perlegere; (quod tamen cito me facturum spero:) adeóque nihil est quod eâ de re dicendum habeo. Videtur autem, ni fallor, ad 'eumèchanian' tetragonismi vero proximi collimare; saltem prout ex levi inspectione conjectare licet. Caeterum Vale, Vir Erudite, et meo nomine saluta etiam Dominum Schotenium quam humanissimè: et scias denique, si tibi placuerit inceptam hanc familiaritatem continuare, gratissimum id futurum esse
John Wallis à Christiaan Huygens.Appendice au No. 227.La lettre se trouve à Leiden, coll. Huygens. Postquam Epistolam absolveram, subijt animum, tibi forsan non ingratum fore si calculum illum apponerem cujus et suprà et in nuperis meis ad Dominum Schotenium | |||||||||||||||
| [ 339 ] | [ v ] |
| mentio facta est, quo easdem ego me dixi juxta methodum meam rationes invenisse quas tu habes in 'Exetasei' tua: adeoque libet illum breviter hic adjungere. |

|
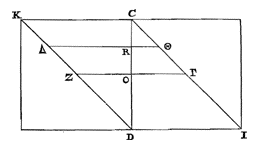
| Retentâ igitur constructione tuâ, eâque quam pagina 35, et alibi habes figurâ 1): Placet quantitatem rectae CD, aliarumque ipsi aequalium, notâ r insignire. Erit igitur CR = ¼ r, CO = ½ r, DO = CD − CO = r − ½ r = ½ r, DR = CD − CR = r − ¼ r = ¾ r. Item RΘ = ¼ r, OΓ = ½ r, OZ = r − ½ r = ½ r, RΔ = r − ¼ r = ¾ r. Et proinde (juxta methodum nostram.) |
| Solidum KΘ = | + ½ CR × RΘ × CK = + ½ × ¼ r × ¼ r × r = 1/32 r³ | | = 5/192 r³. | |
| − 1/3 CR × RΘ × RΘ = − 1/3 × ¼ r × ¼ r × ¼ r = − 1/192 r³ | ||||
| Solidum KΓ = | + ½ CO × OΓ × CK = + ½ × ½ r × ½ r × r = 1/8 r³ | | = 1/12 r³ = 16/192 r³. | |
| − 1/3 CO × OΓ × OΓ = − 1/3 × ½ r × ½ r × ½ r = − 1/24 r³ |
| Solidum MΞ = | + 1/3 ES × SΞ × EM = + 1/3 × ¼ r × 1/16 r × r = 1/192 r³ | | = 53/15360 r³. | |
| − 2/4 ES × SΞ × ES = − 2/4 × ¼ r × 1/16 r × ¼ r = − 1/512 r³ | ||||
| + 1/5 ES × SΞ × SΞ = + 1/5 × ¼ r × 1/16 r × 1/16 r = 1/5120 r³ | ||||
| Solidum MΣ = | + 1/3 EP × PΣ × EM = + 1/3 × ½ r × ¼ r × r = 1/24 r³ | | = 1/60 r³ = 256/15360 r³. | |
| − 2/4 EP × PΣ × EP = − 2/4 × ½ r × ¼ r × ½ r = − 1/32 r³ | ||||
| + 1/5 EP × PΣ × PΣ = + 1/5 × ½ r × ¼ r × ¼ r = 1/160 r³ |
|
Ergo solidum ΛΣ (= solidum MΣ − solidum MΞ) = 256−53/15360 r³ = 203/15360 r³. Ideoque Solidum MΞ . Solidum ΛΣ :: 53/15360 r³ . 203/15360 r³ :: 53 . 203. Quae est tuarum rationum altera.
1) Ces deux figures, que l'on ne trouve pas dans la lettre, sont reproduites de l'Exetasis, page 35. |
| [ 340 ] | [ v ] |
|
Calculi fundamentum habetur in propositionibus 64, 66, 73, nostrae Arithmeticae Infinitorum 2).
2) Dit werk was in 1655 te Londen gedrukt. Het komt voor in de Opera Mathematica [1695] van J. Wallis, vol. 1, p. 355-458 onder de titel: Arithmetica Infinitorum sive Nova Methodus Inquirendi in Curvilineorum Quadraturam, aliaque difficiliores Matheseos Problemata. Anno 1655 typis edita. [ Ex. GWLB met aantekeningen van Chr. Huygens.] |
| [ 379 ] | [ v ] |
|
J. Wallis à Christiaan Huygens.4 février 1656.La lettre se trouve à Leiden, coll. Huygens. Clarissime Vir, Tuis ad me Hagae Comitis datis Junii 13. 1655. responsorias meas eodem mense repositas te accepisse confido. Quid de curvis nostris antehac propositis judicandum erit, a te fortasse accipiemus, ubi quem cum his literis mitto libellum 3) pervolveris. Qua ratione illae ad circulum pertineant, (quod tu, ut ais, summopere videre desideras,) in eodem libello percipias, quem ut tibi ea de re satisfaciam mittendum putavi. Quid de nostro inibi tradito Tetragonismo senserint Geometrae, mihi non ingratum erit audire; et numcubi erratum sit. Et, speciatim, quid de nostra senserint quaesitae quantitatis designatione propositione 191 4) traditâ, et Scholio tum praecedente tum subsequente: num scilicet satisfaciat, an nova adhuc sit exquirenda. Exemplarium alterum ut ad Dominum Schotenium transmittas oro, eumque meo nomine salutes. Quid de Geometria Domini Hobbes senserim; ex ejusdem Elencho meo 5), nuper edito, vos vidisse confido. Caeterum ne rebus tuis nimis sim molestus, manum de tabulâ*), ubi me fuero professus
3) J. Wallis. [De sectionibus conicis, 1655 ... De angulo contactus, 1656 ...] Arithmetica Infinitorum, seu nova Methodus Inquirendi in Curvilineorum Quadraturam, aliaque difficiliora Matheseos Problemata. Oxoniae. 1656 [Dedicatio: 19 Julii 19, 1655]. 4) [...] le célèbre produit pour 4/π: | |||||||||||||||
3 x 3 x 5 x 5 x 7 x 7 x 9 x 9 x 11 x 11 x 13 x 13 x etc.
2 x 4 x 4 x 6 x 6 x 8 x 8 x 10 x 10 x 12 x 12 x 14 x etc.
|
|
5) J. Wallis. Elenchus geometriae Hobbianae. Oxoniae. 1655. Ce livre fut l'origine d'une polémique longue et assez envenimée entre Wallis et Hobbes [>]. [ *) Apelles, selon Plinius.] 6) Huygens ne reçut cette lettre que le 9 mars 1656. Voir la Lettre No. 269 [p. 389]. |
| [ 392 ] | [ v ] |
|
Christiaan Huygens à J. Wallis.[15 mars 1656.] 1)La minute et la copie se trouvent à Leiden, coll. Huygens.
Christ. Hug. S. D. Priores literas tuas 2) Vir Praestantissime quibuscum una pagellam de Circuli Quadratura mittebas, Parisijs accepi, idque tibi pridem significassem. Verum usque adeo irrequietam atque occupatam ea in urbe vitam egimus ut non satis officij meminisse licuerit; multoque minus studiorum hujuscemodi quae otium et solitudinem poscunt. Eodem verò tempore ab alio Viro Nobili 3) eadem ista vestra pagella Londino mihi missa est, simulque Hobbij Philosophia nova 4) quam ubi primum examinare concessum est continuo paralogismum eum animadverti quo parabolicae lineae rectam aequare contendit calculoque refutavi. Deinde alia quoque notavi quae nihilo rectius se habebant, autoremque ingenio minimè defaecato*) praeferebant. Quin te miror eum dignum judicasse quem tam prolixè refelleres, etsi non sine voluptate elenchum tuum perlegi, doctum equidem atque acutum. Alteras à te literas jam triduo habui verum libros de Quadratura quos adjunxisse scribis adhuc expecto idque supra quam credi possit mihi molestum est. Caeterum quia in superscriptione Epistolae nulla librorum mentio facta est credo fortasse alia via venturos. neque adhuc omnem spem deposui. Si accepero summa cum attentione evolvam, libereque tibi judicium perscribam meum hoc enim te expetere existimo. Mitto cum his observationem nostram de Saturni noviter detecto comite°), quam Astronomis vestris exhibeas velim; continet ea explicationem aenigmatis ejus quod praecedenti epistolae subjunxeram. litterae enim transpositae erant, Admovere oculis distantia sidera nostris UUUUUUU, CCC RR HNBQX, quae haec verba efficiunt: SATURNO LVNA SVA CIRCUNDUCITUR DIEBUS SEXDECIM HORIS QUATUOR. sed has horas nunc comperi auferendas. Quid vero tuo anagramma significetur avidè expecto. teque rogo ut explices. Vale. 1) Voir la Lettre No. 277 [>]. 2) Voir la Lettre No. 227 [<]. 3) C'est W. Brereton. Voir la Lettre No. 225 [p. 334]. 4) Six Lessons to the Professors of Mathematicks of the Institution of Sr. Henry Savile. By Th. Hobbes. London 1656. in-4o [txt; translation/adaptation of Elementorum philosophiae sectio prima De corpore, 1655]. [ *) Correction T. II, 631: defuratus - defaecatus.] [ °) Christiani Hugenii de Saturni Lunâ observatio nova, Hag. Com. Adrianus Vlacq. 1656. 4 pp. in 4o. XV, 165; aussi dans: P. Borel, De vero telescopii inventore (paru en 1656) II, 62-3.] |
| [ 396 ] | [ v ] |
|
J. Wallis à Christiaan Huygens.1 avril 1656.La lettre se trouve à Leiden, coll. Huygens.
Accepi nudius tertius, Clarissime Vir, literas tuas, Hagae Comitis datas Martii 15 stilo novo et gratulor tibi visa tua. Ne autem te solum ea vidisse putes, faciet (credo) aenigma nostrum, anno praeterito indicatum, his literis scriptum, |
9 1 5 4 9 1 1 12 3 6 6 7
aaaaaaaaa b ccccc dddd eeeeeeeee f h iiiiiiiiiiii lll mmmmmm nnnnnn ooooooo
5 1 11 13 8 17 1
ppppp q rrrrrrrrrrr sssssssssssss tttttttt uuuuuuuuuuuuuuuuu x a)
|
|
quod sic exponas licet; Saturni Comes quasi lunando vehitur. Diebus sexdecim circuitu rotatur. Novas nuper Saturni formas Telescopo vidimus primitus. Plura speramus. Ad plenum vero Saturni phasium systema rectius colligendum, faciet fortasse tuarum cum nostris jam inde ab anno 1649 praestitis observationum collatio. Quod autem ad phasin Saturni mox exspectandum attinet; an hac forma
|
| [ 397 ] | [ v ] |
accepisse. Quippe cujus curae a me mandati Bibliopola noster 1), se a Domino Pulleyn 2) Bibliopola Londinensi certò accepisse ait, tum literas tum libros ab illo missos fuisse tibi tradendos; nec dubitare se quin ad te tutò perventuri fuerint. Fieri autem posse arbitror, ut libri illi, cum majori suorum sarcina missi, tardius aliquanto quam literae adveniant. Monendum tamen Dominum Pullenium curabo, ut sicubi adhuc lateant, repetitis literis tradendos curet. Vale, Vir Clarissime, et amare pergas
a) Prolixam hoc anagramma commentus erat Wallisius, ut postquam meum exposuissem, eundem sensum ex suo illo elicere posset. Sed fraudem istam viri alij ingenui, ex Societate Regia, inter quos Moraius, mihi fassi sunt, jam ante suspectam. [Chr. Huygens.] ["Dr Wallis (a most ill-natured man, an egregious lyer and backbiter, a flatterer and fawner on my Lord Brouncker and his Miss, that my Lord may keepe up his reputation)", John Aubrey, Brief Lives, 'William Holder', cf. Catching Proteus.] 1) Thomas Robinson était alors le Academical publisher de l'Université d'Oxford. 2) Octavian Pulleyn, libraire, vivait à Londres dans St Paul's churchyard. Vingt ans plus tard, on trouve un autre libraire, portant le nom de Octavian Pulleyn jr. |
| [ 401 ] | [ v ] |
|
J. Wallis à Christiaan Huygens.17 avril 1656.La lettre se trouve à Leiden, coll. Huygens.
Johannes Wallis Geometriae Professor Oxoniensis S. a) Quam a Te nuperrimè accepi, de Saturni Luna [<], paginam, Hagae-Comitis praeterito Mense Martis typis impressam et divulgatam, (quâ de sententiam, meam ante unam aut alteram septimanam indicatam, te accepisse confido;) Ego Honoratissimo Domino Paulo Nelio 1) Equiti Aurato (hujusmodi observationibus exercitatissimo) per communem amicum Christophorum Wren 2), Magistrum Artium, Collegij Omnium Animarum Oxoniae Socium, (qui cum Honoratissimo Equite saepenumero observationes junctim instituit) communicavi. Testantur illi se stellam illam jam olim multoties vidisse (et, credo, multò antè quàm Tu eam notaveris;) idque non solum Tubis longioribus, putà pedum 22, 24, 28, (cujusmodi praesto habent accuratissimos,) sed et pedum duodecim. Quod moneo, tum propter illud epistolae ad me tuae, anno superiori, Perspicillum mihi paravi ipse nuper 12 pedum longitudine, quo praestantius aliud vix puto reperiri, quum nemo antehac viderit quod ego nuper observavi; scribitur autem transpositis literis in hunc modum ADMOVERE &c. tunc illud impressae paginae, Cum autem longiora etiam hisce Telescopia, utpote triginta aut quadraginta pedum ab alijs fabricari 1) Sir Paul Neile [1613 - 1686], un des premiers qui fréquentèrent les assemblées de Gresham College, d'où est sorti plus tard le Royal Society; longtemps il y a été membre du Council. [^] 2) Sir Christopher Wren [... 1632 - 1723]. Il fut nommé professeur d'astronomie au collège de Gresham (1657) et à Oxford (1660). Dès 1665 il se voua à l'architecture [...]. [^] |
| [ 402 ] | [ v ] |
| dicantur; aliquid aut vitris vitij inesse, aut haec eadem non debita proportione mutuo respondere, credibile est: Neque enim aliàs hucusque aciem eorum effugisset novus Saturni satelles [^]. quae posteriora verba epistolam meam priori tuae responsoriam, de hujusmodi apud nos vitris monentem, respicere videantur. Ubi autem in eadem impressa pagina, haec habes, Nostrum quo Saturni asseclam reperimus, quinquagies diametrum rei visae multiplicat, duodenos pedes aequans; cui postea duplum longitudine construximus, multiplicatione centupla; Omnino eà sumus opinione, ut vel in multiplicatione aestimandà deceptus fueris (quod potius crediderim) vel haud ita commode vitra tua sint disposita; cum ea multiplicatio isti distantiae videatur minime convenire. Sed et hoc insuper tibi indicandum putant: Saturni phasibus observandis, se praestantissimis tubis instructos, jam per septem annos continuos invigilasse; omnesque ipsius interea temporis phases diligenter notâsse; quas et accuratè depictas habemus, adjunctis observandi temporibus. Quo tempore, fuerunt observatae, saltem duodecim, ab invicem admodum distinctae, Saturni formae, (omissis quae in transitu ab his ad illas fuerint istis intermediae;) quarum fere pars media, plane aliae sunt ab ijs omnibus quas vel Galilaeus 3), Gassendus 4), Fontana 5), Hevelius 6), vel etiam Richelius 7), aut quem novimus quispiam alius, adhuc indicavit. Atque huc quidem respexit ille, quem tecum, mense Junio superioris anni 8), Gryphum deposui, deinceps ubi opus futurum esset deposcendum sub hac formà, b) |
9 1 5 4 9 1 1 12 3 6 6 7
aaaaaaaaa b ccccc dddd eeeeeeeee f h iiiiiiiiiiii lll mmmmmm nnnnnn ooooooo
5 1 11 13 8 17 1
ppppp q rrrrrrrrrrr sssssssssssss tttttttt uuuuuuuuuuuuuuuuu x.
|
|
3) [...] Continuazione del Nuncio Sidereo [... Opere di Galileo ... Vol. 2, parte 2], Bologna, 1655. 4) [...] Commentarii de Rebus Coelestibus. [...] Opera Omnia IV, p. 444-479. [Institutio astronomica, 1656, fig.] 5) [... Novae caelestium terrestriumque rerum observationes, Neap. 1646.] 6) [... Selenographia, 1647, fig.]. 7) Giovanni Battista Riccioli [... 1598 - 1671 ...], Almagestum novum [... 1651, p. 488, 712, 724]. 8) Voir la Lettre No. 227 [<]. |
| [ 403 ] | [ v ] |
|
(Quem sic exponas velim. Saturni comes quasi lunando vehitur. Diebus sexdecim circuitu rotatur. novas nuper Saturni formas Telescopo vidimus primitus. Plura speramus.) Quo eodem mense hunc tuum mecum deposuisti Gryphum [<] Admovere oculis distantia sidera nostris VVVVVVVCCCRRHNBQX. Quem jam nuperrime sic exponendum docuisti. Saturno luna sua circunducitur diebus sexdecim, horis quatuor. Quas quidem horas quatuor cum tu tandem auferendas agnoscas, periodus tua emendata nostrae convenit. Quod autem ad Saturni phases attinet, quas observavimus; videmus nobis eam inde Saturni et ansularum suarum figuram collegisse, eamque motuum hypothesin, quae Phaenomenis illis satisfaciat; an autem et omnibus deinceps observandis, haud audacter adhuc pronunciamus. Eousque enim versatilem illum invenimus, ut nec dum sciamus num omnes illius formae nobis adhuc fuerint conspectae. Quod quidem in causa fuit quod observationes illae nondum in publicum fuerint emissae. Dum autem tu ex tuis observationibus praeterito praesentique anno collectis, te posse integrum Saturni systema perficere, videris existimare; metuo ne omnino frustra sit; quippe illud unius aliusve anni negotium esse haud videtur. Et quanquam ex comparatis Galilaei observatione, quâ Saturnum plane rotundum conspexit; alijsque Hevelij et Gassendi, qui id iterum observarunt anno 1642; similique aspectu per quatuor menses jam proxime elapsos; colligendum videatur, Saturni corporis semicircuitum absolvi anno currente decimo quarto, vel ad summum decimo quinto: Tamen alia adhuc, propter varias ipsius conspectas formas, in auxilium advocanda omnino erunt priusquam systema congruum perficiatur. Quae non, ut diligentiae tuae quicquam derogatum velimus dicta sunto, sed ut cautius procedas. Quod autem ad mox expectandam Saturni phasin attinet; videtur nobis duos propediem nodulos utrinque protuberantes expectandos, positu ad Eclipticam obliquo, se sensim in brachia porrecturos; quae ubi satis fuerint porrecta non tam utrinque singula, quam utrinque bina post interjectam viaculam coeuntia, videbuntur. Atque haec sunt quae de praesenti negotio tibi judicavimus indicanda. Vale.
a) Rp. 26 Apr. Respondi 28 apr. 10) [Chr. Huygens]. b) Decipisset me puto si potuisset [Chr. Huygens]. 9) Wallis se servait du Vieux Style, à cette époque encore usité en Angleterre. 10) Voir la Lettre No. 294. | ||||||
| [ 423 ] | [ v ] |
|
Christiaan Huygens à J. Wallis.mai 1656.La minute et la copie se trouvent à Leiden, coll. Huygens. Clarissimo Viro Domino J. Wallisio Christianus Hugenius S. D. 1656 Maj. Ad epistolam meam quacum una observationem de Saturni luna tibi misi binis 1) respondisti, quarum ultimas accepi nudius tertius. In prioribus rursus librorum mentionem facis qui adhuc nusquam comparent: summoque desiderio me torquent. Saturni satellitem cum vos quoque observantes, ex anagrammatis vestri explicatione intelligerem a) non leviter me arrexit rei novitas, nihil minus enim quam sententiam ejusmodi istis occultari literis suspicabar. Neque tamen mirum est cum praestantissima habueritis telescopia observationibusque invigiletis, si idem quod ego, vidistis. Gratulor itaque invicem vobis qui et hoc et plura alia telescopijs vestris rerum coelestium arcana deprehenderitis. Sed et hoc gratulor, quod vir illustris P. Nelius pridem mihi fama notus perspicillis conficiendis studium suum et scientiam eximiamque peritiam commodat. Tali adjutore non frustra plura speratis. Si novum planetam ante me detexisse eum constiterit, nequaquam ipsi hanc gloriam invidebo. Ita vero ostendere poterit, si conscios adducat quibus olim inventum hoc vel apertè vel enigmate aliquo involutum concrediderit. concedam. Quod cum jam olim se vidisse dicit, fieri potest ut viderit quidem sed planetam esse nesciverit*), observationesque annotare neglexerit, quod et mihi evenisse certo scio.1) Voir les Lettres Nos. 277 et 280. [ *) Systema Saturnium (1659), 26: "in Anglia D. Paulus Nelius eques cum Clarissimo Wrennio ipso jam Anno 1655, sibi animadversum quandoque asserunt, nec tamen Planetam esse cognovisse donec a nobis essent admoniti."] |
| [ 424 ] | [ v ] |
|
Nihil mihi gratius facere possis, quam si varias Saturni phases depictas exhibeas, ut experiar quomodo hypothesi meae accommodentur, quam transpositis literis observationi subjeci namque ego nullam adhuc notavi praeter eam quae fuit anno praecedenti. Vos autem mirabilem diversitatem deprehendisse videmini 7 annorum spatio. Sed fieri quoque potest ut diversae magnitudinis perspicillis, quae eaedem sunt figurae non eaedem videantur. Quae de 30 aut 40 pedum longitudine attigi, non magis ad vestra telescopia pertinebat quam quae et Norimbergi, Augusta Vindelicorum 2), et Romae 3) fabricantur, arbitrabar scilicet mea solum acute cernere, uti et vos de vestris procul dubio credideritis. Verun tamen nunc quoque praestare meum vestris dicendum videtur illud inquam quod 24 pedibus producitur, quoniam incredibilem fatemini multiplicationem, quam statui centuplam. Nam quod videor vobis in aestimatione deceptus fuisse, fortasse aequius judicium ferretis, si videritis quantâ diligentiâ theoremata dioptrica conscripserim accuratissima ratione ex vitrorum foci distantia, eorumque in tubo situ quantum magnitudo visa veram exuperet colligere didici, idque propositis lentibus quotlibet, adeo ut experimento non opus habeam. Expertus tamen sum magno telescopio meo, quod si Saturnum intuear, discus ejus paulo minor apparet, quam lunae facies nudo oculo spectata, quippe lunâ prope Saturnum stante, utramque speciem in unum convenire facio, tumque evenit, ut altera alteram propemodum contegat. Fateor tamen, nisi hâc ratione comparatio instituatur, sed solus spectetur Saturnus, longe minorem videri, neque multum excedere Imperialis 4) quae maxima apud nos moneta est, magnitudinem. Sed hujuscemodi aestimatio plane incerta est atque ab alijs causis pendet. Porro incommode lentes nostras compositas ne existimes, cum clara et quam maximè distincta omnia nobis exhibeant. Nodulos Saturno adnatum iri ut expectem, nequaquam patitur hypothesis mea quae an frustra futura sit, eventus docebit. Certe non sine magna verisimilitudine eam amplexus sum. Vale et me Domino Nelio commenda.
a) NB. Deceperat me 'pseudoanagramma' confingens Wallisius; nam literis quas confuso ordine miserat, tunc demum cum mei anagrammatis explicationem accepisset, similem utcunque sensum effinxit, ut postea confessus est [Chr. Huygens]. [ Huygens semble encore croire l'assertion de Wallis en juillet 1656: lettre à Roberval (p. 457), à Hevelius (p. 463), et à Chapelain (p. 473).] 2) Par Johann Wiesel. Voyez la Lettre No. 206. 3) Par Giuseppe Campani, que nous rencontrerons plus tard dans sa correspondance avec Chr. Huygens [V, 195, fig. Sat. 1664; et VII, 362, 1673]. 4) Rixdale hollandaise, de la grandeur environ d'une pièce de cinq francs. |
| [ 458 ] | [ v ] |
|
Christiaan Huygens à J. Wallis.[21 juillet 1656] 1).La minute et la copie se trouvent à Leiden, coll. Huygens.
Libros quos ad me miseras posteaquam diu hic in officina bibliopolae delituissent tandem paucis abhinc diebus accepi, cumque Domino Schotenio exemplar alterum 1) Cette date résulte de la réponse, la Lettre No. 325. |
| [ 459 ] | [ v ] |
deferri curassem, rescripsit ille se jam ante sibi comparasse. Quod sanè et ipse fecissem, si scivissem Lugduni illos venire. Plurimum tibi debeo, quod mentionem nostri facere voluisti nec sine laude 2), quando operosam Gregorij a Sto Vincentio quadraturam 'exetasei' mea labefactam judices. Nihil mihi exoptatius evenire potuit praesertim hoc tempore, cum novis conatibus easdem illas ineptias propugnari cernam. Ainscomius enim Jesuita Patris Gregorij discipulus librum à se editum mihi nuper misit, quo quotquot sunt novae quadraturae adversarij refelluntur, scilicet atque ego inter caeteros. Huic igitur cum respondebo tuum quoque judicium opponam, quin imo et unicam progressionem [<] abs te repertam 3.3.5.5.7.7 &c. 2.4.4.6.6.8magno istorum molimini praeferre non verebor. Caeterum de lucubrationibus tuis ut quid sentiam penitius intelligas, videreris mihi haud exiguum fecisse operae praetium, etiamsi nihil praeter eam quam dixi progressionem attulisses, utique si vera est. Vellem autem ut vel ipse tu vel alius examen per numeros quod ego aliousque perduxi ulterius prosequeretur, nam demonstrationes per inductionem quas adhibes, nondum tam perspicuae aut certae mihi videntur ut absque haesitatione illis confidere liceat. In propositione 191*) non benè intelligo qua ratione ex eo quod β/α minor sit quam 2/1, conficias eandem β/α minorem esse quam √(2/1). Itaque haec quaeso mihi explica, neque mirare quod adhuc ea non sim assecutus, cum uti dixi nuper admodum libros tuos acceperim. Lineam Curvam propositione 192 propositam non existimo te cuiquam pro geometrica approbaturum, nam quae geometricae sunt in ijs inter duo quaelibet data in ipsis puncta possunt quotcunque alia investigari, quod in tuis secus est. Neque ad determinationem sufficit quod adjunxisti, ut aequabilis sit, non hinc inde subsultans, quoniam et ex circumferentiae particulis tales componere licet, quae transeant per ea puncta quae in curva tua definita sunt. Quae de angulo contactus°) prolixe disputas in ijs plane tecum sentio, semperque visum est perperam ipsi affingi anguli nomen vel certe quantitatem. De Conicis 3) Schotenius mihi scripsit 4) ea sibi perlecta esse atque admodum probari. ego vix inspicere coepi. animadverti tamen algebraicis demonstrationibus te uti, quae sane compendiosae sunt, optandumque esset ut ab omnibus intelligerentur. Ego ejusmodi demonstrationes nuper adhibui in tractatu quodam de aleae ratiocinijs, quem Schotenius una cum suis quae nunc edit operibus in lucem dare proposuit. Occasionem mihi dederant in Gallia Mathematici quidam, qui quaestiones hujusmodi mihi proposuerant. Nempe quoto jactu aliquis una tessera qualibus vulgo nunc utuntur, senarium se daturum contendere possit. item duabus 2) Voyez la "Dedicatio" de l'ouvrage Arithmetica infinitorum. [ *) Cf. Ex. GWLB: marginalia de Huygens, p. 178 (image ci-dessous), 179; et plus.] |

|
[ °) De angulo contactus et semicirculi, 1656. Cf: 'Horn angle'.] 3) Voyez l'ouvrage cité dans la Lettre No. 286, note 2 [p. 410: De Sectionibus Conicis, 1655]. 4) Voir la Lettre No. 313 [p. 453]. |
| [ 460 ] | [ v ] |
|
tesseris quoto jactu senarios duos. et plurimas praeterea hujus generis, quibus resolvendis non admodum facile fuit prima principia reperire. Saturnum ansas suas non recepisse vos quoque isthic procul dubio observasti. Vale. |
| [ 476 ] | [ v ] |
|
J. Wallis à Christiaan Huygens.22 août 1656.La lettre se trouve à Leiden, coll. Huygens.
Joh. Wallis S. Literas tuas (Vir Clarissime) Julij 21 datas ego ante quatuor dies accepi, quibus ob Clarissimi Viri Domini Erasmij Bartholini jam proxime abituri 1) decessum necesse habeo raptim respondere. Quod tibi non displicuerit qualiscunque opera mea, quinimo accepta fuerit, etiam gaudeo. Ubi aliquid haerere tibi visum est, id facili, spero, negotio amovebitur, quippe illud non profundae difficultatis videtur, sed quod ipse amovisse possis, iterata inspectione, aut etiam de facto amoveris forsan priusquam hae ad te perveniant. Progressionem illam quod attinet 3.3.5.5.7.7 &c. 2.4.4.6.6.8 &c.cur non in dubium vocem id facit, quòd continuâ methodo eò pervenerim, ut ubi totum processum examinaveris reperies: nec uspiam videam ubi de errore admodum dubitandum videatur. Quod autem examen per numeros fieri suadeas, quamquam ea de re minus ipse fuerim solicitus, id tamen jam sua sponte praestitit Honoratissimus Dominus, Vicecomes Bronker 2), (cujus ad propositionem 191 mentionem facio) 1) En septembre il était sur son retour en Hollande, voir la Lettre No. 335 [p. 492]. 2) Lord Viscount William Brouncker [... vers 1620 - 1684 ...]. |
| [ 477 ] | [ v ] |
| quò tam suam quam meam designationem comprobet; atque examen illud ad decimum usque locum continuavit, omniaque ex voto succedentia invenit; scilicet rationem Perimetri ad Diametrum inde colligit |
/ majorem quam 3.14159,26535,69 + \
{ } ad 1.
\ minorem quam 3.14159,26536,96 + /
|
|
Sed et in toto processu, alternatim, nunc excedentem nunc deficientem, ut oportuit; utrinque autem ad justam continuè propius accedentem: ut non dubium sit quin eò ritè pervenerim investigando. Quod autem ad Demonstrationis modum per Inductionem attinet, quem novo exemplo in Geometriam me putas introducere. Quamquam non negem me aliquid hic novi praestitisse; cum ea methodo frequentius videar atque apertius usus; non tamen id plane novum est, aut omni exemplo caret quo me hoc nomine defendam, nam et id frequentius fit quam tu forte primo aspectu putaveris: praesertim in Arithmeticis. Nempe ubi seriatim non videant aliquousque procedere, nec quicquam in contrarium urgeri posse praevideant, universaliter rem asserunt etiam accurati Mathematici. Videbis id aliquoties (ni fallet memoria) a Domino Briggio 3), Praecessore olim meo meritissimo, inter Regulas eas quas praeposuit Tabulis suis Logarithmicis 4), ubi de Constructione Canonis leges exhibet; nec tamen eapropter Canonis Logarithmici fides suspecta fuit. Similliter in ijs quae a Vieta praestita sunt de Angularibus Sectionibus 5); ubi postquam series aliquousque comprobata est, quod superest in Tabellas conjicitur in infinitum continuendas. Sed et ipsae Tabellae numerorum qui in artificiosa Potestatum Genesi*) usui sunt, non nisi ex incepta serie, aliquousque comprobatâ calculo, deinde continuantur in infinitum; quae non aliter quam Inductione probantur. Verum et in alijs propositionibus Geometricis id passim usu venit: ut, verbi gratia, in 34 propositione 5 Elementorum ex editione Clavij 6), (alijsque passim). Nempe propositio incipit. Si sint 3) Henry Briggs [... 1561 - 1630 ...]. 4) Arithmetica Logarithmica [...] 1624. 5) Voyez Francisci Vietae Opera Mathematica [... ed. F. van Schooten], p. 287-304. [ *) De numerosa potestatum purarum, atque adfectarum ad Exegesin resolutione, p. 162.] 6) Euclidis Elementorum Libri XV Accessit liber XVI [... 1607]. |
| [ 478 ] | [ v ] |
|
quotcunque magnitudines &c. Deinde probat inductione, Sunto, inquit, tres &c. Deinde sunt quatuor &c. Et tum subjungit, Eadem arte concludes ea consequi in quinque, sex, septem &c. Non secus atque nos, puta propositione 19. Sint termini duo; proveniet ratio 1/3 + 1/6, quod demonstratur ex calculo. Sicut tres, proveniet ratio 1/3 + 1/(2x6). quod item demonstratur ex calculo. Et sic deinceps quousque libet, nempe ubique demonstratur ex calculo. Imo, inquam, (quod tamen non omnes animadvertunt) vix ulla est in tota Geometria propositio quae aliter quam inductione demonstratur. Exemplum esto 121*). Propositio Euclides, Super data quavis recta terminata, triangulum aequilaterum constituere. Deinde exponit unam rectam AB, et super hanc constructum triangulum demonstrat esse aequilaterum: Tum subsumendum relinquit, (quod nempe quilibet supplere debet,) Atque eadem methodo, super quamvis aliam rectam ita construetur triangulum, et pariter demonstrabitur. Ergo, In quavis &c. Nec quidem aliter constat vis istius aliusve fere demonstrationis, quam ex suppositione, quod nullus casus in contrarium urgeri possit cui non applicabitur exposita demonstratio: quam qui suppositionem negaverit, tenetur casum contrarium assignare. Similiter, ubi nos non unum quidem aut duo exempla, sed 6, 7, 8 &c. (vel etiam, quod in adversarijs nostris aliquando fecimus, ad locum etiam centesimum, aut ultra;) idem universaliter obtinere contendimus, nec quisquam exemplum in contrarium urgere poterit: Non est cur ea pro legitima demonstratione non habeatur. Sed et pares inductiones videbis ad 20e 6, et 1e 12 7), et passim alibi. Et apud Archimedem fere ubique. Nempe in Theoremate sive Problemate ubi casuum numerus certus est atque finitus; solent Mathematici singulos casus sigillatim probare. At ubi numerus casuum est infinitus, satis habent, si, ostensis paucis, methodum item ostendant qua qui volet quotlibet demonstret alias. Nec quidem alias demonstrationes ejusmodi propositiones patiuntur; utut illud nonnunquam planius, nonnunquam magis tectè instituatur. Dum autem ais ad propositionem 191. te non bene intelligere quo pacto ex eo quod β/α minor sit quam 2/1, conficiam eandem β/α minorem esse quam √(2/1); et similiter γ/b minorem esse quam 4/3, adeoque et quam √(4/3). Neutiquam assequeris, ob festinationem, quod illic traditur, quod tamen iteratâ inspectione non dubito quin statim videris. Nempe quia β/α = 2/1, concludo β/a (non β/α) minorem quam √(2/1). Velim itaque ut haec verba mea, Ideoque (cum rationes continuè multiplicantes perpetuo decrescant) erit [ *) Prop. I-1.] 7) Wallis désigne ici probablement la proposition 20 du livre 6, et la proposition 1 du livre 12 des Eléments d'Euclide. |
| [ 479 ] | [ v ] |
| β/α | minor duarum a/α × β/a = β/α = 2/1 | ideoque | minor quam √(2/1) | |||
| major duarum β/a × b/β = b/a = 3/2 | major quam √(3/2) |
|
quasi sic dicta intelligas. Quoniam seriei α. a. β. b. γ. c. &c. rationes β/α. b/a. γ/β. c/b. &c. perpetuo decrescunt, (ut superius patet,) adeoque et, interpolatione regulari continue factâ, rationes quae componunt has expositas, nempe a/α, β/a, b/β, γ/b, c/γ, δ/c &c. continue item decrescunt: Erit ideo β/a minor duarum a/α, β/a, componentium rationem β/α = 2/1; adeoque eadem β/a (cum sit minor duarum componentium rationum β/α) erit minor quam √(β/α) = √(2/1) (nam duarum rationum aequalium, componentium aliam, utraque erit ratio subduplicata compositae: et inaequalium eandem compositam componentium, minor quidem, minor erit quam ratio subduplicata; et major, major). Item eadem β/a (cum sit major duarum β/a, b/β, componentium rationem b/a = 3/2) erit major quam √(b/a) - √(3/2). Similiter est item |
| γ/b | minor duarum b/β, γ/b, componentium γ/β = 4/3 | ||
| major duarum γ/b, c/γ, componentium c/b = 5/4 |
| ideoque eadem γ/b | minor quam √(γ/β) = √(4/3). | |
| major quam √(c/b) = √(5/4). |
|
Denique quod ad ultimum tuum quaesitum attinet. Num scilicet curva propositionis 192. sit Geometrica, necne. Nescio num de hac sola, an de alijs illam propositionum sequentium, et scholij, curvis procedat. Si enim reliquas pro Geometricis admiseris, de hac, eadem ratione constabit, ut mox videbitur. Sin eas non admiseris; dicendum erit quatenus ego id contendam. Nempe de Scholij ultimi curvis 2a, 4a, 6a, 8a &c. res statim erit in confesso; quarum nempe singula puncta determinantur per aequationes monadicam 8) lateralem 9), quadraticam, cubicam, &c. quae quidem ad propositionem 189. exhibentur. De reliquis 1a, 3a, 5a, 7a &c. videntur illae postulare
8) C'est ainsi que l'auteur appelle une équation exprimant l'invariabilité d'une fonction. 9) Wallis emploie ici la locution vieille "aequatio lateralis" pour "équation du premier degré". |
| [ 480 ] | [ v ] |
|
aequationes, quae sint istis intermediae; puta 3a postulat aequationem naturae intermediae inter monadem et lateralem; 5a, aequationem quae sit inter lateralem et quadraticam intermedia; 7a, ea quae est inter quadraticam et cubicam intermedia. Has autem ego aequationes, utut determinatae in rerum natura quantitatis existimem, puto tamen ineffabiles 10) esse; quamquam interim earum unâ cognitâ, reliquas etiam cognosci certum sit, ex demonstratis propositionibus 188, 189. Si verò quod ineffabiles sint illae aequationes, vel saltem adhuc esse videantur, propterea nec lineas eas pro Geometricis agnoscas, utut sint in rerum natura satis determinatae, licet nobis haud effabili aliqua aequatione determinandae; ego litem de nomine non movebo. Videntur autem hujusmodi aequationes ita se ad effabiles habere, atque numeri surdi ad veros. Si autem et eas lineas pro Geometricis habendas putes, (nam pro Geometrarum arbitrio vel sunt vel non sunt ita dicendae,) erit et pariter Geometrica ea quae est Propositionis 192. Est enim haec ab earum aliquâ facile derivabilis, quippe 1 . 3/2 . 15/8 . 105/48 &c. numeri curvae propositionis 193. (quae eadem est cum scholij curva tertia) ducti in Geometrice proportionales 1. 4. 16. 64 &c, constituunt numeros curvae propositionis 192. adeoque et numerorum illis interpolandorum mutuo ductu, fiunt qui hic interpolandi; adeoque si curva propositionis 193. sit linea Geometrica, erit item et linea propositionis 192. Habenda itaque est pro Geometricâ, vel utraque vel neutra. Si autem lineae genus, in natura rerum utcunque determinabile ego verbis in propositione 192. non satis determinaverim; id verborum penuriae in re difficili dandum est. De Saturno nil novi dicendum habeo. Quando ipsius restituentur ansulae, res exspectamus magis quam praedicimus. Saturni phases hic visas, spero, aeri incisas me tibi brevi communicaturum. Id nempe se curaturum mihi est pollicitus Dominus Christophorus Wren. Interim Vale.
Raptim Oxoniae
10) L'auteur désigne par ces mots des équations de degré 1/2 , 3/2 , 5/2 , qu'on pourrait nommer des équations "sourdes", ou irrationnelles. |
| [ 494 ] | [ v ] |
|
Christiaan Huygens à J. Wallis.[septembre 1656].La minute et la copie se trouvent à Leiden, coll. Huygens.
Tu quidem Vir Clarissime nova quotidie prodis diligentiae tuae specimina cujusmodi sunt ea quae nuper mihi per Dominum Trommium 1) deferenda curasti, [ *) Langius (Epistola ad Meibomium, 1656).] 1) Abraham van der Trommen Jansz. (Trommius) [... 1633 - 1719 ...]. Après avoir fini ses études de théologie, il alla voyager (1655) et fréquenta diverses universités. [...] |
| [ 495 ] | [ v ] |
| pro quibus ingentes tibi gratias ago. at ego a tempore aliquo prorsus perfunctorie in studijs hisce versor, et fere in totum cessator evasi, dum valetudini parum firmae curam adhibere cogor, atque et moderavi mihi ab intenta ista meditatione. Nunc cum quasi postliminio et mathesin, et Eruditorum virorum commercium repetam, video te imprimis esse ad quem plurima scribendi materia suppetat. Ac primum quidem illis tuis literis respondebo quas mihi Dominus Bartholinus tradidit [<]. e quibus illud primum intelligere gavisus sum tetragonismum tuum arithmeticum, supputatione Domini Bronker comprobari. Hinc enim manifesto constat recte sese habere propositiones omnes tuas, quibus eo pervenisti. |