Vandaar dat geweldige verlangen, waardoor ik tot nu toe werd geprikkeld, u iets in een brief aan te geven, opdat wij, die in leeftijd niet veel verschillen, en in dezelfde wiskundige studies plezier hebben, door wederzijdse briefwisseling meer bekend worden met elkaar.
Daarbij kwam de voor mij verbazende aanbeveling van u, van de uitstekende heer en zeer geleerde Meetkundige, de eerwaarde pater Gregorius van St-Vincent, wiens genegenheid u met uw oordeel over zijn eerste kwadratuur in hoge mate voor u hebt gewonnen. Ook mij bevalt dat geschrift van u voorzover het de kwadratuur betreft, maar (neemt u mij niet kwalijk dat ik het zeg) niet geheel; omdat ik zie dat u op een ander doel mikt dan waarop de schrijver zich richt.
U meent immers (zoals uit uw voorwoord blijkt) dat pater Gregorius van oordeel is dat de eerste kwadratuur sterker is dan alle andere; terwijl hij daarin toch veeleer de mogelijkheid van de kwadratuur tracht aan te tonen, dan deze metterdaad te geven.
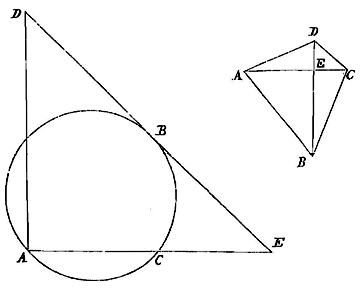
![]() Wanneer hij namelijk in de eerste kwadratuur 6 grootheden neemt, waarvan de vier eerste, A, B, en C, D, rechtlijnig zijn, de twee laatste, E, F, echter cirkelvormig, en laat zien dat de verhouding van het eerste paar, A, B, zoveel keer door vermenigvuldiging de verhouding bevat van het tweede, C, D, als deze verhouding van het tweede de verhouding bevat van het derde paar, E, F; wanneer de schrijver dit laat zien, zeg ik, is het niet zijn bedoeling echt een getal te geven, dat aanduidt hoeveel keer de verhouding van de eerste grootheden, A, B, door vermenigvuldiging de verhouding bevat van de tweede, C, D (dit blijkt immers onmogelijk te zijn volgens dezelfde uiteenzetting waarmee hij die propositie afleidt) om daaruit te weten te komen hoeveel keer de verhouding van het tweede paar, C, D, de verhouding bevat tussen het derde paar grootheden, E, F.
Wanneer hij namelijk in de eerste kwadratuur 6 grootheden neemt, waarvan de vier eerste, A, B, en C, D, rechtlijnig zijn, de twee laatste, E, F, echter cirkelvormig, en laat zien dat de verhouding van het eerste paar, A, B, zoveel keer door vermenigvuldiging de verhouding bevat van het tweede, C, D, als deze verhouding van het tweede de verhouding bevat van het derde paar, E, F; wanneer de schrijver dit laat zien, zeg ik, is het niet zijn bedoeling echt een getal te geven, dat aanduidt hoeveel keer de verhouding van de eerste grootheden, A, B, door vermenigvuldiging de verhouding bevat van de tweede, C, D (dit blijkt immers onmogelijk te zijn volgens dezelfde uiteenzetting waarmee hij die propositie afleidt) om daaruit te weten te komen hoeveel keer de verhouding van het tweede paar, C, D, de verhouding bevat tussen het derde paar grootheden, E, F.
Maar de hele uiteenzetting richt zich er alleen op, te laten zien met kracht van de opgestelde uiteenzetting dat het met die zes grootheden zo gesteld is, dat een eigenschap die past bij een gevonden verhouding tussen de eerste grootheden, A, B, in verband met een verhouding tussen de tweede, C, D, ook past bij de verhouding tussen de tweede, C, D, in verband met een gevonden verhouding tussen de derde, E, F; en dus, daar de derde grootheden cirkelvormig zijn, dat een evenredigheid van een kromme met een rechte mogelijk is.
Dit is het doel van de eerste kwadratuur*), als ik de bedoeling van pater Gregorius goed begrepen heb uit een aan mij geadresseerde brief. De volgende lijken de zaak met een makkelijkere uiteenzetting tot stand te brengen; tot de uiteindelijke strekking ervan zal men echter niet gemakkelijk komen.
Ikzelf ben het afgelopen jaar begonnen de tweede te onderzoeken, die volgens de schrijver makkelijker is dan de andere, waarvan ik wel de strekking en de volgorde heb gevolgd, als ik me niet vergis; maar op één punt blijf ik nog steeds steken, waardoor ik geen goedkeuring kan geven van de hele uiteenzetting.
Overigens, hoe het ook zij met de kwadratuur, het Opus Geometricum is mijns inziens zo belangrijk, als de wereld tot nu toe nauwelijks van enige Meetkundige heeft gezien; en dat zal iedereen met mij eens zijn die meer aan de waarheid toegeschreven wil zien, dan aan een door enig verkeerd gevoel vooropgezette eigen mening.
Dit had ik, illustere en geleerde jongeheer, waarvan ik vond dat het in mijn eerste brief aan u geschreven moest worden. Als U, ster van de eerste grootte van deze tijd, vindt dat ik het verdien dat u ook van mij houdt, en dat u mij deelgenoot maakt van uw zaken en studies (naar ik begrijp meetkundige theorema's, ik hoor dat u heel scherpzinnige
[ *) Deze eerste kwadratuur wordt besproken in T. 11, 'Voorbericht', p. 277-280.
In het werk van Gregorius (1647), p. 891, 'Proportionalitatum geometricarum pars secunda': De similitudine proportionum inter rationes existentium; en p. 1114-1134: 'Prima circuli quadratura'.]
 Maar ik heb ook enige zuiver Meetkundige proposities verzameld, waarvan ik voor u deze ene wil opschrijven, die ik onlangs heb gevonden bij het construeren van het
Maar ik heb ook enige zuiver Meetkundige proposities verzameld, waarvan ik voor u deze ene wil opschrijven, die ik onlangs heb gevonden bij het construeren van het 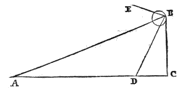
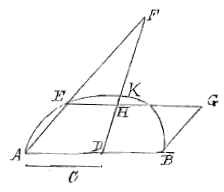
 Gegeven een cirkel met boog ABC, die in drieën gedeeld moet worden. Laar een liniaal langs het middelpunt D van de cirkel de koorde AC snijden in E, en de boog ABC in F, op zo'n manier dat de getrokken koorde CF gelijk is aan de rechte CE.
Gegeven een cirkel met boog ABC, die in drieën gedeeld moet worden. Laar een liniaal langs het middelpunt D van de cirkel de koorde AC snijden in E, en de boog ABC in F, op zo'n manier dat de getrokken koorde CF gelijk is aan de rechte CE.  4)
4)
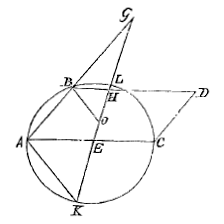 De cirkel wordt voltooid als ALCK en GE wordt doorgetrokken tot aan de omtrek in K; en A wordt met K verbonden, en daarmee evenwijdig wordt BO getrokken. De driehoeken AEK en BHO zijn dus gelijkvormig; en omdat AE gelijk is aan EK, zijn ook gelijk BH en HO; maar ook HG en HD zijn aan elkaar gelijk, volgens constructie, dus de hele OG is gelijk aan BD, dat wil zeggen aan diameter AC of LK. En als de gemeenschappelijke LO wordt afgetrokken blijven over de aan elkaar gelijke GL en OK.
De cirkel wordt voltooid als ALCK en GE wordt doorgetrokken tot aan de omtrek in K; en A wordt met K verbonden, en daarmee evenwijdig wordt BO getrokken. De driehoeken AEK en BHO zijn dus gelijkvormig; en omdat AE gelijk is aan EK, zijn ook gelijk BH en HO; maar ook HG en HD zijn aan elkaar gelijk, volgens constructie, dus de hele OG is gelijk aan BD, dat wil zeggen aan diameter AC of LK. En als de gemeenschappelijke LO wordt afgetrokken blijven over de aan elkaar gelijke GL en OK. 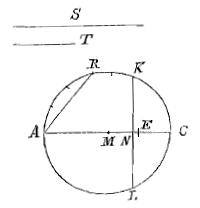 AC wordt in E zodanig verdeeld dat geldt: zoals S tot T, zo is AE tot EC; en in de cirkel ABCD wordt een rechte AR aangebracht die gelijk is aan het verschil van AE en EC.
AC wordt in E zodanig verdeeld dat geldt: zoals S tot T, zo is AE tot EC; en in de cirkel ABCD wordt een rechte AR aangebracht die gelijk is aan het verschil van AE en EC. 
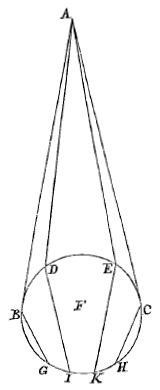 Laat een of ander punt van de zon zijn A, waar vandaan op het bolletje BCDE de stralen AB en AC vallen die dit raken in de punten B en C; AD en AE echter snijden het.
Laat een of ander punt van de zon zijn A, waar vandaan op het bolletje BCDE de stralen AB en AC vallen die dit raken in de punten B en C; AD en AE echter snijden het.  Hij schrijft: als een bol, b.v. A, stoot tegen een eraan gelijke bol B die in rust is, en A heeft vier delen snelheid, dat hij er op B één zal overdragen en met de drie overige zal terugspringen. Ik zal echter bewijzen [
Hij schrijft: als een bol, b.v. A, stoot tegen een eraan gelijke bol B die in rust is, en A heeft vier delen snelheid, dat hij er op B één zal overdragen en met de drie overige zal terugspringen. Ik zal echter bewijzen [ Maar wat er zou moeten gebeuren wanneer de bollen ongelijk zijn, zoals wanneer C in grootte de helft is van bol D, die in rust is, en die hij ontmoet met vier delen snelheid, hoeveel er moet overgaan op D en hoeveel voor C overblijft, dat heb ik nog door niemand passend bepaald gezien, of althans zodat het met mijn berekeningen overeenkwam.
Maar wat er zou moeten gebeuren wanneer de bollen ongelijk zijn, zoals wanneer C in grootte de helft is van bol D, die in rust is, en die hij ontmoet met vier delen snelheid, hoeveel er moet overgaan op D en hoeveel voor C overblijft, dat heb ik nog door niemand passend bepaald gezien, of althans zodat het met mijn berekeningen overeenkwam. 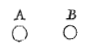 Van hem neemt u ook zelf terecht af datgene, van een andere aard, wat hij beweert in het geval waarin een bolletje A, gelijk aan een bolletje B, met vier delen snelheid botst tegen het bolletje B:
Van hem neemt u ook zelf terecht af datgene, van een andere aard, wat hij beweert in het geval waarin een bolletje A, gelijk aan een bolletje B, met vier delen snelheid botst tegen het bolletje B:
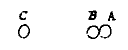 als tegen twee gelijke bollen A en B die tegen elkaar liggen, in rechte lijn een derde bol C stoot, zelfs als hij afgeschoten is met het geweld van een kanon, dan zal A zeker naar de andere kant bewegen, en B zal zonder enige beweging blijven; wat heel verbazend is, dat zo'n kleine bol stand houdt tegen de onstuimigheid van een krijgswerktuig b), voor het geweld waarvan al het andere wijkt.
als tegen twee gelijke bollen A en B die tegen elkaar liggen, in rechte lijn een derde bol C stoot, zelfs als hij afgeschoten is met het geweld van een kanon, dan zal A zeker naar de andere kant bewegen, en B zal zonder enige beweging blijven; wat heel verbazend is, dat zo'n kleine bol stand houdt tegen de onstuimigheid van een krijgswerktuig b), voor het geweld waarvan al het andere wijkt. 
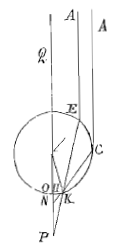 Deze straal onderschept althans met de as, die aan AE zelf evenwijdig is, een boog KO van ongeveer 20½ graden, als de bol uit water bestaat. Noodzakelijkerwijze gelijk aan de helft van die waaronder de halve diameter van de regenboog aan de hemel wordt gezien.
Deze straal onderschept althans met de as, die aan AE zelf evenwijdig is, een boog KO van ongeveer 20½ graden, als de bol uit water bestaat. Noodzakelijkerwijze gelijk aan de helft van die waaronder de halve diameter van de regenboog aan de hemel wordt gezien. 
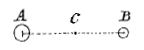 Ik wil vragen dat hij u zegt wat er zal gebeuren wanneer de bollen A en B met gelijke snelheid elkaar in C tegenkomen, en als de grootte van A driemaal die van B is. Ik geloof nauwelijks dat hij zal vinden dat bol A tot rust zal komen, en dat B met tweemaal de snelheid die hij tevoren had
Ik wil vragen dat hij u zegt wat er zal gebeuren wanneer de bollen A en B met gelijke snelheid elkaar in C tegenkomen, en als de grootte van A driemaal die van B is. Ik geloof nauwelijks dat hij zal vinden dat bol A tot rust zal komen, en dat B met tweemaal de snelheid die hij tevoren had