 Maar ditzelfde zullen we ook bereiken door een kleine opening voor het oog te plaatsen, omdat dan als het ware maar aan één van de stralen, die van afzonderlijke punten van het object anders in onnoemelijk aantal naar de pupil lopen, doorgang verleend wordt.
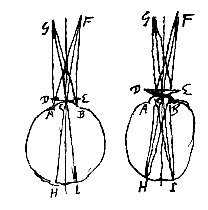
Maar ditzelfde zullen we ook bereiken door een kleine opening voor het oog te plaatsen, omdat dan als het ware maar aan één van de stralen, die van afzonderlijke punten van het object anders in onnoemelijk aantal naar de pupil lopen, doorgang verleend wordt. Want stel dat stralen die van de uiterste punten van het object vertrokken zijn, op de oogpupil AB vallen, zoals die, komend uit de punten F en G. En dat voor het oog een nauwe opening C in een plaatje gezet wordt, die slechts als het ware afzonderlijke stralen FC en GC toelaat, die dan de achterkant van het oog ontmoeten in de punten H en I. Dan zullen hier de afzonderlijke punten van het object afgetekend worden, waaruit de stralen FA, FC, FB, en GA, GC, GB voortgekomen zijn. En wegens het weren van alle stralen behalve FC en GC zal de afbeelding scherp zijn, en daardoor ook het zicht.
Anderzijds, met hetzelfde gestelde, maar met weglating van het doorboorde plaatje, zetten we in plaats daarvan een lens DE heel dichtbij het oog, die een scherp zicht zal geven. Ik zeg dat het object gezien zal gaan worden met dezelfde grootte als eerst, en met dezelfde plaatsing. Want omdat door het midden van de lens — waarvan de dikte verwaarloosd wordt — de stralen FC en FG langs rechte lijnen doorgaan {* volgens voorstel XXIII}, is het duidelijk dat ze binnen het oog op dezelfde manier lopen, als toen ze hiervoor door de opening C gingen, en dat ze daarom de achterkant van het oog in dezelfde punten H en I zullen ontmoeten.
Doch aangezien gesteld wordt dat door de tussengeplaatste lens DE een scherp zicht ontstaat, is het nodig dat alle stralen die uit G komen, in één punt achterin het oog samenkomen, en zo ook alle stralen die uit F komen. Dus zullen alle van punt G weggegane samenkomen in I, en alle uit F weggegane zullen samenkomen in H; en daarom zullen noodzakelijk die uiterste punten van het object afgetekend worden in H en I. En zo zal de breedte ervan niet anders verschijnen, of men nu voor het oog de lens DE zet, of een heel kleine opening; en ook de plaatsing is dezelfde. Welke dingen bewezen moesten worden.
Dus wanneer we in het volgende de schijnbare grootte ook zullen bepalen in die gevallen waarin een wazig zicht optreedt, zal daaronder verstaan moeten worden die grootte, die onderscheiden wordt na correctie van de wazigheid, hetzij met een lens, hetzij met een heel kleine opening, zoals we al gezegd hebben.*)
*) Eind van de latere versie.
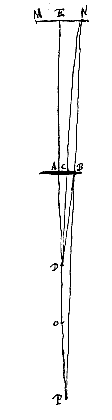 Gegeven een bolle lens AB, waarvan het middelste punt of 'navel' A is, brandpunt O. En het oog D, op de as AO van de lens geplaatst. En als zichtbaar object het lijnstuk NM, evenwijdig met de lens, waarvan het midden E op dezelfde as is. Want als we weten hoeveel dit lijnstuk, of het gedeelte EN ervan, vergroot wordt als het door de lens bekeken wordt, zal ook een willekeurig ander object, dat op die plaats gezet is, zoveel vergroot worden in lengte.
Gegeven een bolle lens AB, waarvan het middelste punt of 'navel' A is, brandpunt O. En het oog D, op de as AO van de lens geplaatst. En als zichtbaar object het lijnstuk NM, evenwijdig met de lens, waarvan het midden E op dezelfde as is. Want als we weten hoeveel dit lijnstuk, of het gedeelte EN ervan, vergroot wordt als het door de lens bekeken wordt, zal ook een willekeurig ander object, dat op die plaats gezet is, zoveel vergroot worden in lengte. 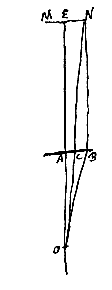 Laat nu het oog in het brandpunt O zelf geplaatst worden, met het object NM dichtbij. We trekken NB evenwijdig aan de as EA, die de lens ontmoet in punt B, en verbinden B met O, en we trekken eveneens NO, die de lens snijdt in punt C. Omdat dus de straal NB evenwijdig is met de as van de lens AB, is het noodzakelijk dat deze gebroken wordt in de richting van brandpunt O, waar het oog geplaatst wordt. En daarom zal punt N alleen door het punt B van de lens gezien worden. Maar punt E, het midden van NM, wordt (zoals eerst) in het middelpunt A van de lens gezien. Dus verschijnt het object NM rechtopstaand; en de schijnbare grootte heeft weer de verhouding BA : CA tot de ware grootte. Maar zoals BA, dat is NE, tot CA, zo is EO tot AO; dus wordt het vergroot gezien volgens de verhouding EO : AO.
Laat nu het oog in het brandpunt O zelf geplaatst worden, met het object NM dichtbij. We trekken NB evenwijdig aan de as EA, die de lens ontmoet in punt B, en verbinden B met O, en we trekken eveneens NO, die de lens snijdt in punt C. Omdat dus de straal NB evenwijdig is met de as van de lens AB, is het noodzakelijk dat deze gebroken wordt in de richting van brandpunt O, waar het oog geplaatst wordt. En daarom zal punt N alleen door het punt B van de lens gezien worden. Maar punt E, het midden van NM, wordt (zoals eerst) in het middelpunt A van de lens gezien. Dus verschijnt het object NM rechtopstaand; en de schijnbare grootte heeft weer de verhouding BA : CA tot de ware grootte. Maar zoals BA, dat is NE, tot CA, zo is EO tot AO; dus wordt het vergroot gezien volgens de verhouding EO : AO.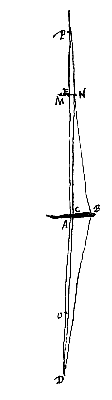 Gegeven als boven de lens AB, en het brandpunt O ervan. Het oog evenwel in punt D van de as, verder dan het brandpunt van de lens af. En bij de twee DO en DA wordt gesteld de derde evenredige DP, volgens voorstel I.
Gegeven als boven de lens AB, en het brandpunt O ervan. Het oog evenwel in punt D van de as, verder dan het brandpunt van de lens af. En bij de twee DO en DA wordt gesteld de derde evenredige DP, volgens voorstel I.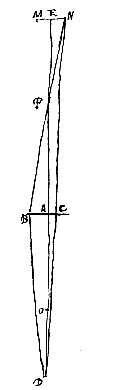 Laat verder in het andere geval het object MN geplaatst zijn voorbij het corresponderend punt P, en maak dezelfde construcies als eerst. Dan zal weer door punt B van de lens het punt N gezien worden, en E door A. Maar als N in werkelijkheid boven punt E is, zal het nu eronder gezien worden, omdat de punten N en B aan tegengestelde kanten van de as EAD liggen. Dus nu zal het object MN omgekeerd verschijnen.
Laat verder in het andere geval het object MN geplaatst zijn voorbij het corresponderend punt P, en maak dezelfde construcies als eerst. Dan zal weer door punt B van de lens het punt N gezien worden, en E door A. Maar als N in werkelijkheid boven punt E is, zal het nu eronder gezien worden, omdat de punten N en B aan tegengestelde kanten van de as EAD liggen. Dus nu zal het object MN omgekeerd verschijnen. 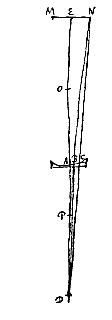 Gegeven een holle lens AC, waarvan de as AO is, en een spreidingspunt O; en het oog is in D op de as geplaatst. En een object MEN aan de andere kant van de lens, zo gelegen als in het vorige theorema. En bij de twee DO en DA wordt een derde evenredige DP gezocht, te nemen aan dezelfde kant als de twee overige. En P is het punt waarnaar stralen gericht zijn die door lens AC afgebogen worden in de richting van het oog D, aangezien stralen die vanaf D naar dezelfde lens komen, zodanig afgebogen worden alsof ze uit P voortkomen {* voorstel I.
Gegeven een holle lens AC, waarvan de as AO is, en een spreidingspunt O; en het oog is in D op de as geplaatst. En een object MEN aan de andere kant van de lens, zo gelegen als in het vorige theorema. En bij de twee DO en DA wordt een derde evenredige DP gezocht, te nemen aan dezelfde kant als de twee overige. En P is het punt waarnaar stralen gericht zijn die door lens AC afgebogen worden in de richting van het oog D, aangezien stralen die vanaf D naar dezelfde lens komen, zodanig afgebogen worden alsof ze uit P voortkomen {* voorstel I.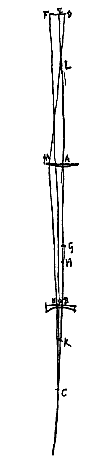 Van twee lenzen staat vast dat er vier variaties of verschillende soorten zijn, want ze kunnen beide bol zijn, of beide hol; of de lens het dichtst bij het oog is hol en de andere bol; of andersom. Daarvan is de tweede soort alleen geschikt om een object te verkleinen: de laatste kan zowel vergroten als verkleinen, maar niet bijzonder goed.
Maar de overige twee hebben verreweg de grootste bruikbaarheid om dingen die men ziet te vergroten, of ze nu ver weg zijn of dichtbij, zoals men al lang geleden door ondervinding te weten is gekomen.
Van twee lenzen staat vast dat er vier variaties of verschillende soorten zijn, want ze kunnen beide bol zijn, of beide hol; of de lens het dichtst bij het oog is hol en de andere bol; of andersom. Daarvan is de tweede soort alleen geschikt om een object te verkleinen: de laatste kan zowel vergroten als verkleinen, maar niet bijzonder goed.
Maar de overige twee hebben verreweg de grootste bruikbaarheid om dingen die men ziet te vergroten, of ze nu ver weg zijn of dichtbij, zoals men al lang geleden door ondervinding te weten is gekomen. 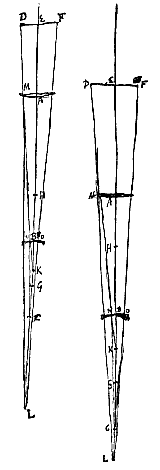
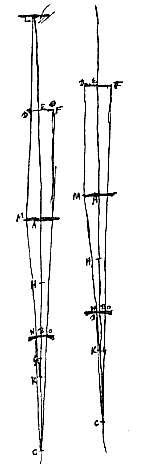 Omdat nu de lenzen gegeven zijn, wordt ook het brandpunt G van de bolle lens gegeven, van stralen die aankomen van de kant van het object, en het spreidingspunt H van de holle lens. Dan wordt eerst bij de twee CH en CB een derde evenredige CK gevonden, te nemen in de richting van H. Vervolgens bij de twee KG en KA een derde evenredige KL, te nemen in de richting van G, tenzij punt K samenvalt met G, in welk geval de evenredige KL weggelaten kan worden.
Omdat nu de lenzen gegeven zijn, wordt ook het brandpunt G van de bolle lens gegeven, van stralen die aankomen van de kant van het object, en het spreidingspunt H van de holle lens. Dan wordt eerst bij de twee CH en CB een derde evenredige CK gevonden, te nemen in de richting van H. Vervolgens bij de twee KG en KA een derde evenredige KL, te nemen in de richting van G, tenzij punt K samenvalt met G, in welk geval de evenredige KL weggelaten kan worden. 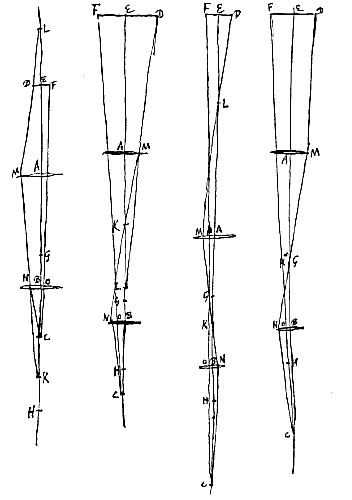
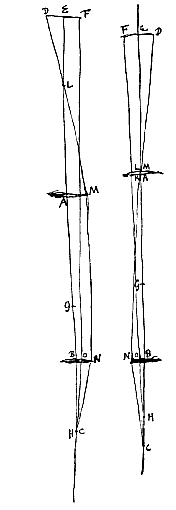 Behalve dat hier het oog C in punt H gezet kan worden, in welk geval punt K niet gevonden wordt, maar AL moet gelijk genomen worden aan AG, en uit punt D moet de rechte DLM getrokken worden die lens A in M ontmoet, en van daaraf moet MN evenwijdig met de as AB gemaakt worden, die lens B ontmoet in N, en N wordt met C verbonden. En het bewijs is als volgt:
Behalve dat hier het oog C in punt H gezet kan worden, in welk geval punt K niet gevonden wordt, maar AL moet gelijk genomen worden aan AG, en uit punt D moet de rechte DLM getrokken worden die lens A in M ontmoet, en van daaraf moet MN evenwijdig met de as AB gemaakt worden, die lens B ontmoet in N, en N wordt met C verbonden. En het bewijs is als volgt: 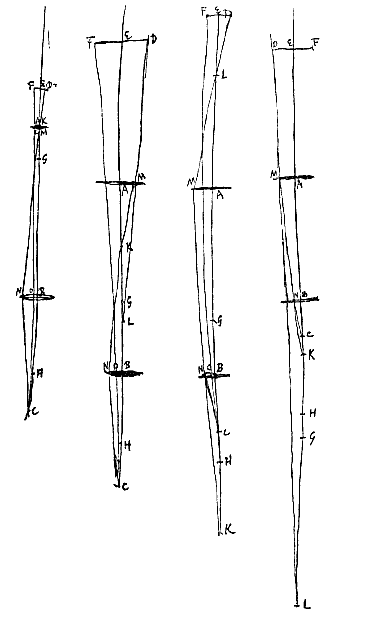
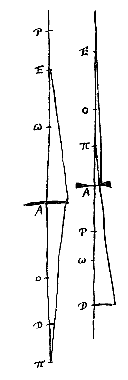 Laat er eerst een enkele lens A zijn, geplaatst tussen het oog in D, en het object in E. Ik zeg dat, als het oog gaat naar E en het object naar D, zonder dat lens A bewogen wordt, het object zo met dezelfde grootte gezien zal worden, als toen het oog in D was en het object in E.
Laat er eerst een enkele lens A zijn, geplaatst tussen het oog in D, en het object in E. Ik zeg dat, als het oog gaat naar E en het object naar D, zonder dat lens A bewogen wordt, het object zo met dezelfde grootte gezien zal worden, als toen het oog in D was en het object in E.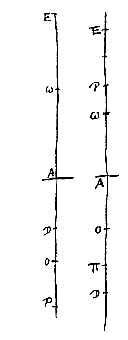 En wat betreft de stand, die in beide posities gelijk verschijnt: dat is wel duidelijk als de lens hol is, aangezien voor iemand die hierdoor kijkt alles rechtopstaand verschijnt [
En wat betreft de stand, die in beide posities gelijk verschijnt: dat is wel duidelijk als de lens hol is, aangezien voor iemand die hierdoor kijkt alles rechtopstaand verschijnt [
 Laat nu de twee lenzen A en B gegeven zijn*), en laat een object in E gezien worden door het oog in C. Ik zeg dat het met dezelfde grootte gezien zal worden indien het oog geplaatst wordt in E, en het object in C. Want we nemen G als brandpunt van lens A, en H van lens B. En met het oog in C correspondeert het punt K met betrekking tot lens B, zodat namelijk CH, CB en CK een continue evenredigheid vormen. Evenzo is met punt K een punt L verbonden met betrekking tot lens A, zodat KG, KA en KL een continue evenredigheid vormen. Daarom, als vanuit C het object gezien wordt dat in E geplaatst is, is de verhouding van schijnbare tot ware grootte die, welke wordt samengesteld uit de verhoudingen HB : HC, AG : GK en EC : EL (zoals aangetoond is in voorstel
Laat nu de twee lenzen A en B gegeven zijn*), en laat een object in E gezien worden door het oog in C. Ik zeg dat het met dezelfde grootte gezien zal worden indien het oog geplaatst wordt in E, en het object in C. Want we nemen G als brandpunt van lens A, en H van lens B. En met het oog in C correspondeert het punt K met betrekking tot lens B, zodat namelijk CH, CB en CK een continue evenredigheid vormen. Evenzo is met punt K een punt L verbonden met betrekking tot lens A, zodat KG, KA en KL een continue evenredigheid vormen. Daarom, als vanuit C het object gezien wordt dat in E geplaatst is, is de verhouding van schijnbare tot ware grootte die, welke wordt samengesteld uit de verhoudingen HB : HC, AG : GK en EC : EL (zoals aangetoond is in voorstel 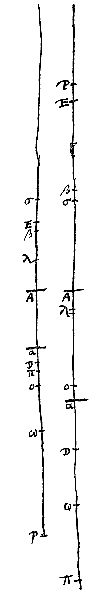
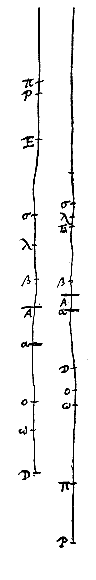
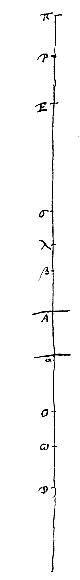 Dit nu is in één geval duidelijk, namelijk als de lens zo dicht bij het oog geplaatst wordt, dat dit tussen de lens en het brandpunt blijft (volgens voorstel
Dit nu is in één geval duidelijk, namelijk als de lens zo dicht bij het oog geplaatst wordt, dat dit tussen de lens en het brandpunt blijft (volgens voorstel 
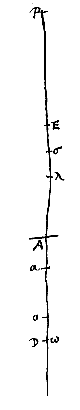 En in het vijfde geval, wanneer O samenvalt met D, valt ook σ in E. En dan is wel voor iemand die door de lens kijkt, als deze in A geplaatst is, de verhouding van schijnbare tot ware grootte die van ED : DA (volgens voorstel
En in het vijfde geval, wanneer O samenvalt met D, valt ook σ in E. En dan is wel voor iemand die door de lens kijkt, als deze in A geplaatst is, de verhouding van schijnbare tot ware grootte die van ED : DA (volgens voorstel 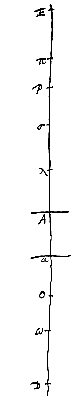 Aangezien dus AO kleiner is dan een vierde van DE, zal de rechthoek AO.DE overtroffen worden door 1/4 van het vierkant DE, d.w.z. door rechthoek DAE, met een zeker overschot. Neem nu Aα, waarvan het kwadraat kleiner is dan dat overschot, en plaats de lens in α. Ik zeg dat het beeld van het object in E omgekeerd gezien zal worden.
Aangezien dus AO kleiner is dan een vierde van DE, zal de rechthoek AO.DE overtroffen worden door 1/4 van het vierkant DE, d.w.z. door rechthoek DAE, met een zeker overschot. Neem nu Aα, waarvan het kwadraat kleiner is dan dat overschot, en plaats de lens in α. Ik zeg dat het beeld van het object in E omgekeerd gezien zal worden. 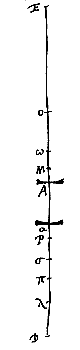 Laat het object geplaatst zijn in E, het oog in D, en M zij het midden van het interval DE. En eerst wordt de holle lens opgesteld in A tussen M en D, daarna evenwel in α, tussen A en D, zodanig dat de afstand αM groter is dan AM. We moeten aantonen dat het beeld van het object in E, bekeken door de lens in A, kleiner is dan bekeken door dezelfde lens in α.
Laat het object geplaatst zijn in E, het oog in D, en M zij het midden van het interval DE. En eerst wordt de holle lens opgesteld in A tussen M en D, daarna evenwel in α, tussen A en D, zodanig dat de afstand αM groter is dan AM. We moeten aantonen dat het beeld van het object in E, bekeken door de lens in A, kleiner is dan bekeken door dezelfde lens in α.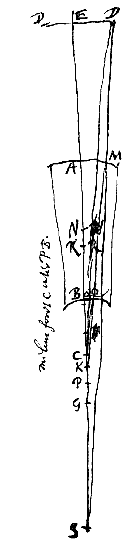 Laat van zo'n samenhangende kijker het bolle oppervlak AM zijn, een gedeelte van een bol met middelpunt N. En het holle oppervlak BQ, met middelpunt P. En het brandpunt van oppervlak AM (oftewel het punt van samenkomst van evenwijdige stralen) is het punt G, terwijl R spreidingspunt is van oppervlak BQ [van evenwijdige stralen die binnen het massieve lichaam lopen]. Verder is het object in de verte DED. Aangetoond moet dus worden dat, wanneer het oog tegen het oppervlak B gehouden wordt, het object DED vergroot wordt met de verhouding AG : GB.
Laat van zo'n samenhangende kijker het bolle oppervlak AM zijn, een gedeelte van een bol met middelpunt N. En het holle oppervlak BQ, met middelpunt P. En het brandpunt van oppervlak AM (oftewel het punt van samenkomst van evenwijdige stralen) is het punt G, terwijl R spreidingspunt is van oppervlak BQ [van evenwijdige stralen die binnen het massieve lichaam lopen]. Verder is het object in de verte DED. Aangetoond moet dus worden dat, wanneer het oog tegen het oppervlak B gehouden wordt, het object DED vergroot wordt met de verhouding AG : GB. Rest slechts nog een ander middel om grotere beelden te maken, en dat is door er voor te zorgen dat stralen die van verschillende punten van het object komen, elkaar zo ver mogelijk van het oog kruisen; maar het is wel onvergelijkbaar, het belangrijkste & meest in aanmerking komende van alle middelen. Want het is het enige dat kan dienen voor ontoegankelijke objecten, even goed als voor toegankelijke, & waarvan de werking geen grenzen kent: zodat men door het toe te passen de beelden steeds groter kan maken, tot in het oneindige.
Rest slechts nog een ander middel om grotere beelden te maken, en dat is door er voor te zorgen dat stralen die van verschillende punten van het object komen, elkaar zo ver mogelijk van het oog kruisen; maar het is wel onvergelijkbaar, het belangrijkste & meest in aanmerking komende van alle middelen. Want het is het enige dat kan dienen voor ontoegankelijke objecten, even goed als voor toegankelijke, & waarvan de werking geen grenzen kent: zodat men door het toe te passen de beelden steeds groter kan maken, tot in het oneindige.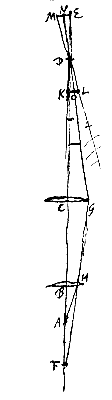 Laat de rechte FE de gemeenschappelijke as zijn waarop het oog komt in punt A, en lenzen in B en C. Verder wordt met stelling I.
Laat de rechte FE de gemeenschappelijke as zijn waarop het oog komt in punt A, en lenzen in B en C. Verder wordt met stelling I.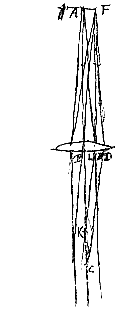 Gegeven de gemeenschappelijke as ABC van een willekeurig aantal lenzen of boloppervlakken, en het lijnstuk AF als object, loodrecht op de as ABC, waarop het punt F zo dichtbij A is, dat het gezien kan worden door het oog in K of C (twee willekeurige punten van de as) geplaatst, en tot een punt teruggebracht; want dat dit mogelijk is staat vast door het vorige voorstel.
Gegeven de gemeenschappelijke as ABC van een willekeurig aantal lenzen of boloppervlakken, en het lijnstuk AF als object, loodrecht op de as ABC, waarop het punt F zo dichtbij A is, dat het gezien kan worden door het oog in K of C (twee willekeurige punten van de as) geplaatst, en tot een punt teruggebracht; want dat dit mogelijk is staat vast door het vorige voorstel.