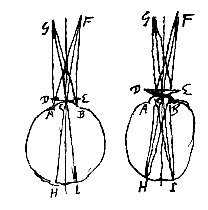
 Sed hoc idem quoque consequemur opposito ad oculum minimo foramine, quia tunc velut uni tantum radiorum qui a singulis rei visae punctis innumeri alioqui ad pupillam feruntur, transitus datur. Ponantur enim radij ab extremis rei visae punctis profecti, ad oculi pupillam AB accidere tanquam ex punctis F, G, venientes. Et objiciatur ante oculum foramen in lamina exiguum C; nonnisi singulos veluti radios FC, GC admittens, qui occurrant oculi fundo in punctis H et I. Itaque hic pingentur puncta rei visae singula, unde manarunt radij FA, FC, FB; et GA, GC, GB. Et propter exclusos ceteros radios praeter FC, GC, distincta erit pictura eoque et visio.
Sed hoc idem quoque consequemur opposito ad oculum minimo foramine, quia tunc velut uni tantum radiorum qui a singulis rei visae punctis innumeri alioqui ad pupillam feruntur, transitus datur. Ponantur enim radij ab extremis rei visae punctis profecti, ad oculi pupillam AB accidere tanquam ex punctis F, G, venientes. Et objiciatur ante oculum foramen in lamina exiguum C; nonnisi singulos veluti radios FC, GC admittens, qui occurrant oculi fundo in punctis H et I. Itaque hic pingentur puncta rei visae singula, unde manarunt radij FA, FC, FB; et GA, GC, GB. Et propter exclusos ceteros radios praeter FC, GC, distincta erit pictura eoque et visio.Rursus ijsdem positis, sed ablatâ lamellâ perforatâ, sit hujus loco lens oculo proxima DE quae distinctam visionem efficiat. Dico eadem qua prius magnitudine eodemque positu spectatum iri visibile. Quia enim per mediam lentem DE, cujus crassitudo tanquam nulla censetur, radij FC, GC, rectis lineis penetrant {* ex propos. XXIII}, manifestum est eos eodem modo intra oculum ferri, atque ante per foramen C transeuntes, atque idcirco oculi fundo in ijsdem punctis H, I occursuros. Cum autem ob interpositam lentem DE distincta visio fieri ponatur, necesse est omnes radios ex G venientes ad unum punctum in fundo oculi convenire, atque ita quoque omnes ex F venientes. Igitur omnes a puncto G egressi convenient in I, et omnes ex F egressi convenient in H. atque idcirco pingentur necessario extrema illa rei visae puncta in H et I. eoque non alia apparebit ejus latitudo objectu lentis DE, ac foraminis minimi; nec non positus quoque idem; quae fuere demonstranda.
Itaque cum in sequentibus apparentem magnitudinem definiemus etiam ijs casibus quibus confusa visio contingit, intelligenda erit ea magnitudo quae cernitur correcta confusione, seu lente seu minimo foramine, ut jam diximus.*)
*) [ Fin de la rédaction postérieure.]
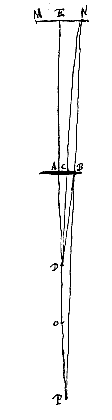 Esto lens convexa AB, cujus medium punctum seu umbilicus A. focus O. Oculus vero D, in axe lentis AO positus. Visibile vero linea NM, lenti parallela, cujusque medium E sit in eodem axe. Quantum enim linea haec vel ejus pars EN augebitur, trans lentem spectata, tantum quoque aliud quodvis visibile, eo loci positum, secundum diametrum augeri sciemus [necesse est]. Porro duabus DO, DA sit tertia proportionalis DP, eritque P punctum oculo D correspondens. Quia enim radij ex puncto D prodeuntes a lente AB ita inflectuntur ut pergant inde tanquam venientes ex P, per prop. [
Esto lens convexa AB, cujus medium punctum seu umbilicus A. focus O. Oculus vero D, in axe lentis AO positus. Visibile vero linea NM, lenti parallela, cujusque medium E sit in eodem axe. Quantum enim linea haec vel ejus pars EN augebitur, trans lentem spectata, tantum quoque aliud quodvis visibile, eo loci positum, secundum diametrum augeri sciemus [necesse est]. Porro duabus DO, DA sit tertia proportionalis DP, eritque P punctum oculo D correspondens. Quia enim radij ex puncto D prodeuntes a lente AB ita inflectuntur ut pergant inde tanquam venientes ex P, per prop. [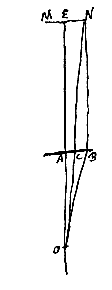 Ponatur autem nunc oculus in ipso foco O, et sit propinquum visibile NM. Ducatur NB parallela axi EA quae occurrat lenti in puncto B, et jungatur BO, itemque NO secans lentem in puncto C. Quia igitur radius NB parallelus est axi lentis AB, eum necesse est refringi versus focum O, ubi oculus ponitur. Quamobrem punctum N spectabitur per solum lentis punctum B. Sed punctum E medium NM spectatur, uti prius, in centro lentis A. Igitur erectum apparet visibile NM; et magnitudo apparens ad veram rursus eam rationem habet quam BA ad CA. Verum ut BA, hoc est, NE ad CA, ita EO ad AO; ergo auctum cernitur secundum rationem EO ad AO.
Ponatur autem nunc oculus in ipso foco O, et sit propinquum visibile NM. Ducatur NB parallela axi EA quae occurrat lenti in puncto B, et jungatur BO, itemque NO secans lentem in puncto C. Quia igitur radius NB parallelus est axi lentis AB, eum necesse est refringi versus focum O, ubi oculus ponitur. Quamobrem punctum N spectabitur per solum lentis punctum B. Sed punctum E medium NM spectatur, uti prius, in centro lentis A. Igitur erectum apparet visibile NM; et magnitudo apparens ad veram rursus eam rationem habet quam BA ad CA. Verum ut BA, hoc est, NE ad CA, ita EO ad AO; ergo auctum cernitur secundum rationem EO ad AO. 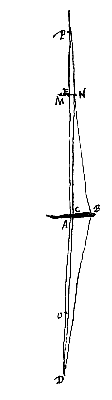 Ponatur ut supra lens AB, et focus ejus O. Oculus autem in puncto axis D, distans a lente ultra focum. Et duabus DO, DA ponatur tertia proportionalis DP, secundum prop. [
Ponatur ut supra lens AB, et focus ejus O. Oculus autem in puncto axis D, distans a lente ultra focum. Et duabus DO, DA ponatur tertia proportionalis DP, secundum prop. [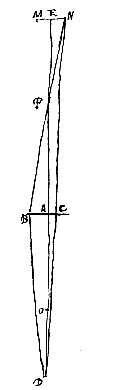 Porro in casu altero sit visibile MN positum ultra punctum correspondens P, et eadem construantur quae prius. Igitur per punctum lentis B rursus aspicietur punctum N, et E per A. Sed si N fuerit reipsa superius puncto E, nunc cernetur inferius, quia ad contrarias partes axis EAD sita sunt puncta E [N] et B. Itaque inversum jam apparebit visibile MN. Ratio autem apparentis incrementi rursus ut in casu priore, erit ea quae BA ad CA; ideoque demonstrandum est rationem hanc, cum visibile propinquum est, componi ex rationibus AO ad OD et ED ad EP. Cum vero longinquum, quod tantum posteriore casu locum habet, eandem esse quae AO ad OD. Quae quidem demonstratio eadem est quae in Theoremate praecedenti.
Porro in casu altero sit visibile MN positum ultra punctum correspondens P, et eadem construantur quae prius. Igitur per punctum lentis B rursus aspicietur punctum N, et E per A. Sed si N fuerit reipsa superius puncto E, nunc cernetur inferius, quia ad contrarias partes axis EAD sita sunt puncta E [N] et B. Itaque inversum jam apparebit visibile MN. Ratio autem apparentis incrementi rursus ut in casu priore, erit ea quae BA ad CA; ideoque demonstrandum est rationem hanc, cum visibile propinquum est, componi ex rationibus AO ad OD et ED ad EP. Cum vero longinquum, quod tantum posteriore casu locum habet, eandem esse quae AO ad OD. Quae quidem demonstratio eadem est quae in Theoremate praecedenti. 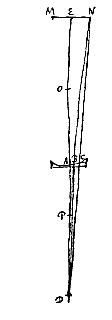 Esto lens cava AC, cujus axis AO; punctum dispergens O; oculus vero in axe positus sit D. Visibile vero ad alteram partem lentis MEN, ita situm uti in Theor. praecedenti. Et fiat duabus DO, DA tertia proportionalis DP, sumenda in partem eandem ac duae reliquae. Eritque P punctum quo tendentes radij flectuntur a lente AC versus oculum D, quoniam qui veniunt ab D in eandem lentem, ita flectuntur quasi procedant a puncto P {* Prop. I.
Esto lens cava AC, cujus axis AO; punctum dispergens O; oculus vero in axe positus sit D. Visibile vero ad alteram partem lentis MEN, ita situm uti in Theor. praecedenti. Et fiat duabus DO, DA tertia proportionalis DP, sumenda in partem eandem ac duae reliquae. Eritque P punctum quo tendentes radij flectuntur a lente AC versus oculum D, quoniam qui veniunt ab D in eandem lentem, ita flectuntur quasi procedant a puncto P {* Prop. I.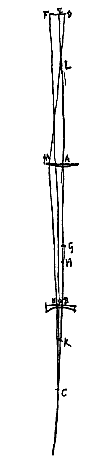 Duarum lentium quatuor esse variationes seu differentias constat [sunt conjugationes], nam vel convexa est utraque, vel utraque cava; vel cava quae propior est oculo, altera convexa; vel contra. quarum secunda differentia minuendo visibile tantum idonea est: posterior et augere potest et minuere, sed nullo egregio effectu. Reliquae vero duae in augendis rerum speciebus, seu remotarum seu propinquarum, multo maximi sunt usus, ut pridem experientia cognitum est. Ratio autem omnium hic manifesta fiet. Nam quamvis positiones utiles tantum persequi propositum sit; tamen et reliquas quivis cum his comparare poterit, quia eodem modo in quavis differentia magnitudo apparens definitur.
Duarum lentium quatuor esse variationes seu differentias constat [sunt conjugationes], nam vel convexa est utraque, vel utraque cava; vel cava quae propior est oculo, altera convexa; vel contra. quarum secunda differentia minuendo visibile tantum idonea est: posterior et augere potest et minuere, sed nullo egregio effectu. Reliquae vero duae in augendis rerum speciebus, seu remotarum seu propinquarum, multo maximi sunt usus, ut pridem experientia cognitum est. Ratio autem omnium hic manifesta fiet. Nam quamvis positiones utiles tantum persequi propositum sit; tamen et reliquas quivis cum his comparare poterit, quia eodem modo in quavis differentia magnitudo apparens definitur.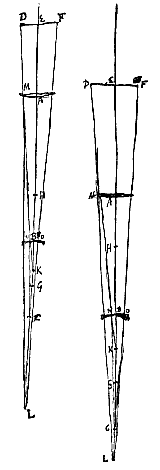
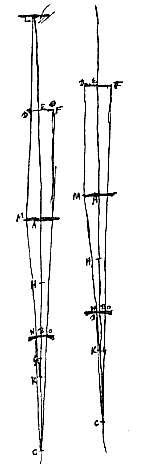 Quia autem datae sunt lentes, datur et convexae focus G, radiorum a parte visibilis advenientium, et concavae punctum dispersus H. Igitur primum inveniatur duabus CH, CB tertia proportionalis CK, versus H sumenda. Deinde duabus KG, KA tertia proportionalis KL, sumenda versus G, nisi contingat punctum K incidere in G, quo casu proportionalis KL omittenda. Dico jam rationem apparentis magnitudinis trans lentes ad eam quae nudo oculo spectaretur, habere rationem compositam ex rationibus HB ad HC, et AG ad GK, et EC ad EL, vel, in casu excepto, ubi deest EL, ex rationibus HB ad HC et EC ad AK.
Quia autem datae sunt lentes, datur et convexae focus G, radiorum a parte visibilis advenientium, et concavae punctum dispersus H. Igitur primum inveniatur duabus CH, CB tertia proportionalis CK, versus H sumenda. Deinde duabus KG, KA tertia proportionalis KL, sumenda versus G, nisi contingat punctum K incidere in G, quo casu proportionalis KL omittenda. Dico jam rationem apparentis magnitudinis trans lentes ad eam quae nudo oculo spectaretur, habere rationem compositam ex rationibus HB ad HC, et AG ad GK, et EC ad EL, vel, in casu excepto, ubi deest EL, ex rationibus HB ad HC et EC ad AK.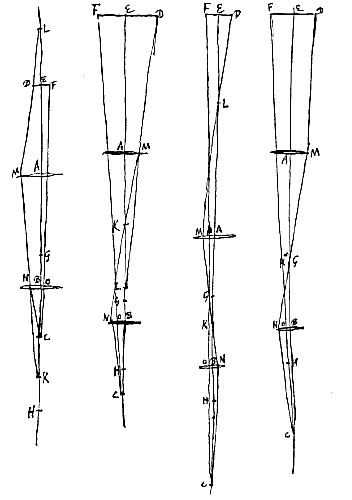
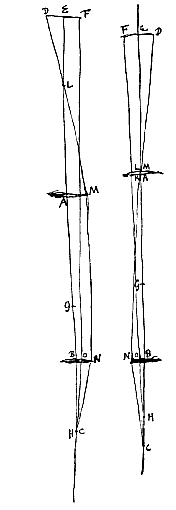 Nisi quod hic potest poni oculus C in puncto H, quo casu punctum K non invenitur, sed sumenda est AL aequalis AG, et ex puncto D ducenda recta DLM occurrens lenti A in M, unde parallela facienda MN axi AB, quae occurrat lenti B in N, et jungenda NC. Demonstratioque erit hujusmodi: Ratio BN ad BO, nempe apparentis magnitudinis ad veram, componitur ex rationibus BN seu AM ad DE et DE ad BO. Quarum AM ad DE eadem est quae AL ad LE: et DE ad BO eadem quae EC ad BC. Ergo ratio BN ad BO componetur ex rationibus AL ad LE et EC ad BC, hoc est, ex rationibus LA ad BC et EC ad EL. Unde si visibile longinquum fuerit, quia tunc ratio EC ad EL est aequalitatis, supererit sola ratio AL ad BC, quae erit apparentis magnitudinis ad veram. Est autem AL foci distantia lentis A, quippe aequalis AG; et BC foci distantia lentis B.
Nisi quod hic potest poni oculus C in puncto H, quo casu punctum K non invenitur, sed sumenda est AL aequalis AG, et ex puncto D ducenda recta DLM occurrens lenti A in M, unde parallela facienda MN axi AB, quae occurrat lenti B in N, et jungenda NC. Demonstratioque erit hujusmodi: Ratio BN ad BO, nempe apparentis magnitudinis ad veram, componitur ex rationibus BN seu AM ad DE et DE ad BO. Quarum AM ad DE eadem est quae AL ad LE: et DE ad BO eadem quae EC ad BC. Ergo ratio BN ad BO componetur ex rationibus AL ad LE et EC ad BC, hoc est, ex rationibus LA ad BC et EC ad EL. Unde si visibile longinquum fuerit, quia tunc ratio EC ad EL est aequalitatis, supererit sola ratio AL ad BC, quae erit apparentis magnitudinis ad veram. Est autem AL foci distantia lentis A, quippe aequalis AG; et BC foci distantia lentis B.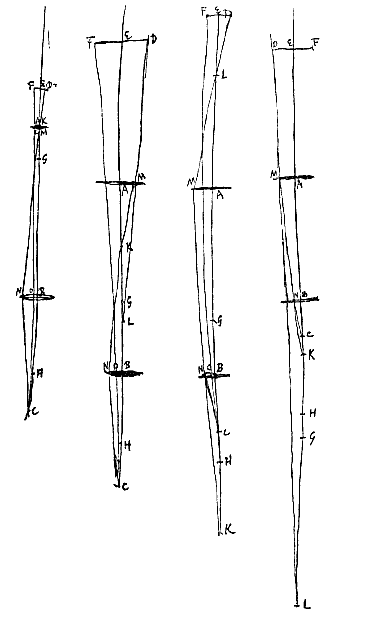
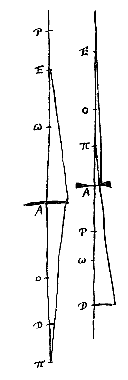 Primum esto lens unica A, posita inter oculum in D et visibile in E. dico si oculus transeat in E et visibile in D, lente A non mota, quod eadem sic magnitudine spectabitur, atque cum oculus erat in D et visibile in E.
Primum esto lens unica A, posita inter oculum in D et visibile in E. dico si oculus transeat in E et visibile in D, lente A non mota, quod eadem sic magnitudine spectabitur, atque cum oculus erat in D et visibile in E.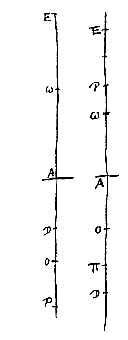 De situ vero, quod similis utrâque positione appareat, id quidem si lens cava sit manifestum est, quoniam omnia per hanc spectanti erecta apparent [
De situ vero, quod similis utrâque positione appareat, id quidem si lens cava sit manifestum est, quoniam omnia per hanc spectanti erecta apparent [
 Proponantur nunc lentes duae A et B*), sitque visibile in E spectatum oculo in C. Dico eâdem magnitudine spectatum iri si oculus in E ponatur et visibile in C. Sit enim lentis A focus G et H lentis B et oculo in C conjugatum punctum K, pertinens ad lentem B, ut sint videlicet in continua proportione CH, CB, CK. Item puncto K conjugatum punctum sit L pertinens ad lentem A, ut sint in continua proportione KG, KA, KL. Itaque cum ex C conspicitur visibile in E positum, ratio apparentis ad veram magnitudinem est ea quae componitur ex rationibus HB ad HC, AG ad GK et EC ad EL ut ostensum fuit propos. [
Proponantur nunc lentes duae A et B*), sitque visibile in E spectatum oculo in C. Dico eâdem magnitudine spectatum iri si oculus in E ponatur et visibile in C. Sit enim lentis A focus G et H lentis B et oculo in C conjugatum punctum K, pertinens ad lentem B, ut sint videlicet in continua proportione CH, CB, CK. Item puncto K conjugatum punctum sit L pertinens ad lentem A, ut sint in continua proportione KG, KA, KL. Itaque cum ex C conspicitur visibile in E positum, ratio apparentis ad veram magnitudinem est ea quae componitur ex rationibus HB ad HC, AG ad GK et EC ad EL ut ostensum fuit propos. [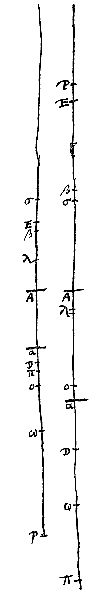
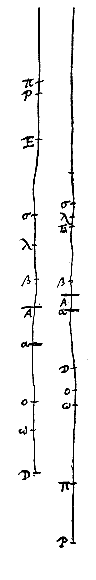
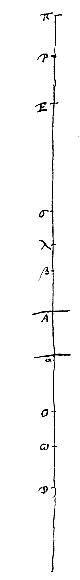 Hoc autem uno casu manifestum est, scilicet si tam propinqua oculo lens collocetur, ut is inter ipsam et focum consistat. per Theorem. [Prop.
Hoc autem uno casu manifestum est, scilicet si tam propinqua oculo lens collocetur, ut is inter ipsam et focum consistat. per Theorem. [Prop. 
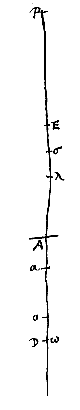 Quinto autem casu cum O incidit in D, etiam σ cadit in E. Et tum quidem per lentem in A positam inspiciendo apparentis magnit.is ad veram ratio est ea quae ED ad DA per prop. [
Quinto autem casu cum O incidit in D, etiam σ cadit in E. Et tum quidem per lentem in A positam inspiciendo apparentis magnit.is ad veram ratio est ea quae ED ad DA per prop. [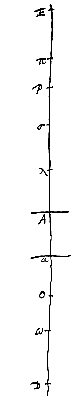 Quoniam ergo AO minor est quarta parte DE, superabitur rectang. sub AO, DE a 1/4 quadrati DE hoc est a rectang.o DAE certo excessu. Ponatur autem Aα cujus quadr. isto excessu minus sit, et constituatur lens in α. dico inversam exhibitum iri visibilis in E speciem. Sint enim reliqua constructa ut in casibus prioribus. Quia igitur DE bifariam aequaliter secta est in A et inaequaliter in α, erit quadr. Aα aequale excessui rectang.i DAE supra rectang. DαE. Idem vero quadratum Aα minus est excessu rectang.i DAE supra rectang. sub DE, AO ex constr. Itaque hic excessus quam ille major est, ideoque rectang. sub DE, AO minus erit rectang.o DαE. Quare minor ratio DE ad Eα quam αD ad AO seu αω. Et per conversionem rationis major ratio ED ad Dα quam αD ad Dω. Sed est πD ad Dα ut αD ad Dω. Ergo πD minor est quam ED. Est autem π punctum oculo in D conjugatum ad lentem in α. Itaque per prop. [
Quoniam ergo AO minor est quarta parte DE, superabitur rectang. sub AO, DE a 1/4 quadrati DE hoc est a rectang.o DAE certo excessu. Ponatur autem Aα cujus quadr. isto excessu minus sit, et constituatur lens in α. dico inversam exhibitum iri visibilis in E speciem. Sint enim reliqua constructa ut in casibus prioribus. Quia igitur DE bifariam aequaliter secta est in A et inaequaliter in α, erit quadr. Aα aequale excessui rectang.i DAE supra rectang. DαE. Idem vero quadratum Aα minus est excessu rectang.i DAE supra rectang. sub DE, AO ex constr. Itaque hic excessus quam ille major est, ideoque rectang. sub DE, AO minus erit rectang.o DαE. Quare minor ratio DE ad Eα quam αD ad AO seu αω. Et per conversionem rationis major ratio ED ad Dα quam αD ad Dω. Sed est πD ad Dα ut αD ad Dω. Ergo πD minor est quam ED. Est autem π punctum oculo in D conjugatum ad lentem in α. Itaque per prop. [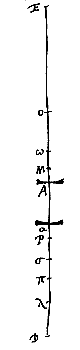 Esto visibile in E positum, oculus in D, sitque punctum M intervalli DE medium; Et primum lens cava constituatur in A inter M et D, deinde autem in α, inter A, D, ita ut distantia αM major sit quam AM. Oportet ostendere quod minor erit species visibilis in E per lentem in A spectati quam per eandem in α. Sit O punctum dispersus lentis in A. Sed ω cum est in α. Et omnia similiter construantur ac in theorem. praecedenti. Itaque eâdem argumentandi ratione devenietur eo, ut ostendere oporteat rectang. OD, EP majus esse rectang.o ωD, Eπ, cum illic ostensum fuerit minus [
Esto visibile in E positum, oculus in D, sitque punctum M intervalli DE medium; Et primum lens cava constituatur in A inter M et D, deinde autem in α, inter A, D, ita ut distantia αM major sit quam AM. Oportet ostendere quod minor erit species visibilis in E per lentem in A spectati quam per eandem in α. Sit O punctum dispersus lentis in A. Sed ω cum est in α. Et omnia similiter construantur ac in theorem. praecedenti. Itaque eâdem argumentandi ratione devenietur eo, ut ostendere oporteat rectang. OD, EP majus esse rectang.o ωD, Eπ, cum illic ostensum fuerit minus [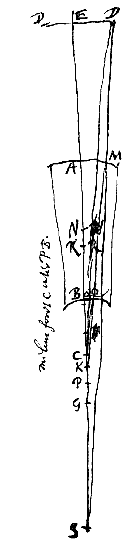 Esto talis specilli continui superficies convexa AM, ex sphaera cujus N centrum. Superficies vero BQ cava centro P. Et focus superficiei AM seu concursus parallelorum sit G punctum. at R punctum dispersus superficiei BQ [radiorum parallelorum qui intra solidum feruntur]. Porro visibile longinquum sit DED. Itaque ostendendum cum oculus superficiei B applicabitur ea proportione visibile DED augeri, quam habet AG ad GB.
Esto talis specilli continui superficies convexa AM, ex sphaera cujus N centrum. Superficies vero BQ cava centro P. Et focus superficiei AM seu concursus parallelorum sit G punctum. at R punctum dispersus superficiei BQ [radiorum parallelorum qui intra solidum feruntur]. Porro visibile longinquum sit DED. Itaque ostendendum cum oculus superficiei B applicabitur ea proportione visibile DED augeri, quam habet AG ad GB. Il ne reste plus qu'vn autre moyen pour augmenter la grandeur des images, qui est de faire que les rayons qui viennent de diuers points de l'obiet, se croisent plus loin qu'il se pourra du fonds de l'oeil; mais il est bien, sans comparaison, le plus important & le plus considerable de tous. Car c'est l'vnique qui puisse seruir pour les obiets inaccessibles, aussy bien que pour les accessibles, & dont l'effet n'a pas de bornes: en sorte qu'on peut, en s'en seruant, augmenter les images de plus en plus jusques a vne grandeur indefinie. Comme, par exemple, d'autant que la premiere des trois liqueurs dont l'oeil est rempli, cause a peu près mesme refraction que l'eau commune, si on applique tout contre vn tuyau plein d'eau, comme EF, au bout duquel il y ait vn verre GHI, dont la figure soit toute semblable a celle de la peau BCD qui couure cete liqueur, & ait meme rapport a la distance du fonds de l'oeil, il ne se fera plus aucune refraction a l'entrée de cet oeil; mais celle qui s'y faisoit auparauant, (& qui estoit cause que tous les rayons qui venoient d'vn mesme point de l'obiet commençoient a se courber dés cet endroit là, pour s'aller assembler en vn mesme point sur les extremités du nerf optique, & qu'ensuite tous ceux qui venoyent de diuers points s'y croisoient, pour s'aller rendre sur diuers points de ce nerf), se fera dés l'entrée du tuyau GI: si bien que ces rayons, se croisans dés là, formeront l'image RST beaucoup plus grande que s'ils ne se croisoient que sur la superficie BCD; & ils la formeront de plus en plus grande selon que ce tuyau sera plus long. Et ainsi l'eau EF faisant l'office de l'humeur K; le verre GHI, celuy de la peau BCD; & l'entrée du tuyau GI, celuy de la prunelle; la vision se fera en mesme façon que si la Nature auoit fait l'oeil plus long qu'il n'est de toute la longueur de ce tuyau.
Il ne reste plus qu'vn autre moyen pour augmenter la grandeur des images, qui est de faire que les rayons qui viennent de diuers points de l'obiet, se croisent plus loin qu'il se pourra du fonds de l'oeil; mais il est bien, sans comparaison, le plus important & le plus considerable de tous. Car c'est l'vnique qui puisse seruir pour les obiets inaccessibles, aussy bien que pour les accessibles, & dont l'effet n'a pas de bornes: en sorte qu'on peut, en s'en seruant, augmenter les images de plus en plus jusques a vne grandeur indefinie. Comme, par exemple, d'autant que la premiere des trois liqueurs dont l'oeil est rempli, cause a peu près mesme refraction que l'eau commune, si on applique tout contre vn tuyau plein d'eau, comme EF, au bout duquel il y ait vn verre GHI, dont la figure soit toute semblable a celle de la peau BCD qui couure cete liqueur, & ait meme rapport a la distance du fonds de l'oeil, il ne se fera plus aucune refraction a l'entrée de cet oeil; mais celle qui s'y faisoit auparauant, (& qui estoit cause que tous les rayons qui venoient d'vn mesme point de l'obiet commençoient a se courber dés cet endroit là, pour s'aller assembler en vn mesme point sur les extremités du nerf optique, & qu'ensuite tous ceux qui venoyent de diuers points s'y croisoient, pour s'aller rendre sur diuers points de ce nerf), se fera dés l'entrée du tuyau GI: si bien que ces rayons, se croisans dés là, formeront l'image RST beaucoup plus grande que s'ils ne se croisoient que sur la superficie BCD; & ils la formeront de plus en plus grande selon que ce tuyau sera plus long. Et ainsi l'eau EF faisant l'office de l'humeur K; le verre GHI, celuy de la peau BCD; & l'entrée du tuyau GI, celuy de la prunelle; la vision se fera en mesme façon que si la Nature auoit fait l'oeil plus long qu'il n'est de toute la longueur de ce tuyau.
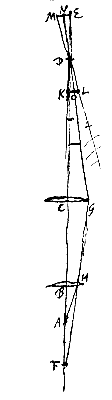 Sit recta FE axis communis in quo oculus ad A punctum, lentes ad B et C. Inveniatur porro ex Theor.... [I.
Sit recta FE axis communis in quo oculus ad A punctum, lentes ad B et C. Inveniatur porro ex Theor.... [I.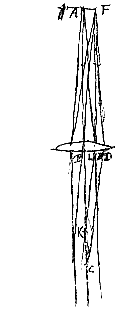 Sit axis communis quotlibet lentium vel superficierum sphaericarum ABC, res visa linea AF, axi ABC perpendicularis in qua punctum F tam propinquum sit ipsi A, ut oculo in K aut C, quibuslibet nempe duobus axis punctis, collocato et ad punctum redacto, in conspectum venire possit. hoc enim possibile esse ex prop. antecedente constat. Dico utroque oculi positu, eadem magnitudine apparituram lineam AF. Quum enim a puncto A manantes radij, trajectis interpositis diaphanis inter se fiant paralleli, etiam ab F puncto egressi inter se paralleli exibunt {* Per Prop.
Sit axis communis quotlibet lentium vel superficierum sphaericarum ABC, res visa linea AF, axi ABC perpendicularis in qua punctum F tam propinquum sit ipsi A, ut oculo in K aut C, quibuslibet nempe duobus axis punctis, collocato et ad punctum redacto, in conspectum venire possit. hoc enim possibile esse ex prop. antecedente constat. Dico utroque oculi positu, eadem magnitudine apparituram lineam AF. Quum enim a puncto A manantes radij, trajectis interpositis diaphanis inter se fiant paralleli, etiam ab F puncto egressi inter se paralleli exibunt {* Per Prop.