|
Rectangulum autem LC, AE aequale est rectangulo LE, CO, quia ut LE ad EA ita LC ad CO; et rectangulum DE, LB aequale est rectangulo EL, DN, quia ut EL ad LB ita ED ad DN. Ergo majus est rectang. LE, CO rectangulo LE, DN, ideoque CO major quam DN.
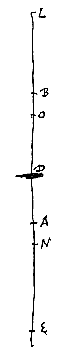
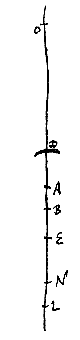 At si crassitudinem lentis CD pro nulla habeamus, uti fere semper in sequentibus fiet, dico puncta concursus parallelorum O et N aequaliter a lente remota esse. Sit enim nunc punctum medium lentis D pro utrisque D et C.
At si crassitudinem lentis CD pro nulla habeamus, uti fere semper in sequentibus fiet, dico puncta concursus parallelorum O et N aequaliter a lente remota esse. Sit enim nunc punctum medium lentis D pro utrisque D et C.
Quia ergo LE ad LA ut LD ad LO, erit et LE ad EA ut LD ad DO, unde rectang. LE, DO aequale rectangulo EA, LD. huic autem aequale est rectang. DE, LB, quia DE ad EA ut DL ad LB, et rursus rectangulo DE, LB aequale rectang. EL, DN, quia ut EL ad LB ita ED ad DN. Ergo rectang. LE, DO aequabitur rectangulo EL, DN; ac proinde DO ipsi DN; quod erat probandum.
Puncta autem O vel N faciliori ratione nunc invenire licebit. Etenim solum inveniendum est punctum L sicut antea, faciendo nimirum ut DL ad LB sit proportio ea quae est refractionis; ac deinde ut BA ad AD ita LB ad DN vel DO*). Quia enim DL ad LB ut DE ad EA, erit per conversionem rationis LD ad DB ut ED ad DA, et permutando LD ad DE ut BD ad DA. Unde et LE ad ED ut BA ad AD. Ut autem BA ad AD ita fecimus LB ad DN. Igitur LE ad ED ut LB ad DN. et permutando, EL ad LB ut ED ad DN. Unde et EL ad EB ut ED ad EN, ideoque N punctum concursus quaesitum; nam hoc antea fuit ostensum. Itaque, in lente vitrea, sicut duae simul convexitatum semidiametri; in menisco autem ut earum differentia, ad alterutram ipsarum, ita reliqua bis erit ad foci distantiam. fit enim tunc LB dupla radij BD, quia DL ad LB ut 3 ad 2 quae in vitro est proportio refractionis. Quod si autem superficies utraque fuerit aequaliter convexa, apparet jam foci distantiam semidiametro convexitatis aequalem fore.
*) La construction conduit aux formules f = R1 R2 / (n – 1) (R1 ± R2)
Propositio XVII
Data lente cava duarum superficierum sphaericarum, punctum dispersus radiorum parallelorum invenire.
|
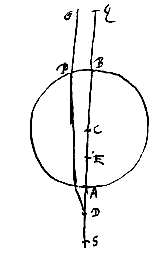 Esto sphaera cujus centrum C axis BA, sectio per centrum circulus BPA. Incidant autem radij paralleli axi BA, ut OP. Dividatur semidiameter CA bifariam in E, et producatur, et habeat CD ad DE proportionem refractionis, eam nempe quae convenit materiae ex qua sphaera componitur. Veluti si crystallina aut vitrea sphaera proponatur oportet rationem CD ad DE esse sequialteram proxime, si vero ex aqua, sesquitertiam. Dico D fore punctum concursus quaesitum*).
Esto sphaera cujus centrum C axis BA, sectio per centrum circulus BPA. Incidant autem radij paralleli axi BA, ut OP. Dividatur semidiameter CA bifariam in E, et producatur, et habeat CD ad DE proportionem refractionis, eam nempe quae convenit materiae ex qua sphaera componitur. Veluti si crystallina aut vitrea sphaera proponatur oportet rationem CD ad DE esse sequialteram proxime, si vero ex aqua, sesquitertiam. Dico D fore punctum concursus quaesitum*).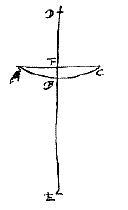 Sit data lens cujus superficies convexa ABC, ex sphaere quae centrum habeat D. Plana autem superficies sit AFC. Atque haec primo radijs parallelis opposita sit. Ducta igitur DBE recta, quae axem lentis referat, hoc est, quae superficiem AFC secet ad angulos rectos, eaque producta ad E, ita ut DE ad EB habeat proportionem refractionis, quae semper data intelligitur: manifestum est E fore punctum concursus quaesitum*). Radij enim axi DF paralleli, cum in superficiem planam AC incidant ad rectos angulos, nullam refractionem ibi patientur, ac proinde paralleli venient ad superficiem ABC. cujus refractione ad E punctum flectentur per [prop.
Sit data lens cujus superficies convexa ABC, ex sphaere quae centrum habeat D. Plana autem superficies sit AFC. Atque haec primo radijs parallelis opposita sit. Ducta igitur DBE recta, quae axem lentis referat, hoc est, quae superficiem AFC secet ad angulos rectos, eaque producta ad E, ita ut DE ad EB habeat proportionem refractionis, quae semper data intelligitur: manifestum est E fore punctum concursus quaesitum*). Radij enim axi DF paralleli, cum in superficiem planam AC incidant ad rectos angulos, nullam refractionem ibi patientur, ac proinde paralleli venient ad superficiem ABC. cujus refractione ad E punctum flectentur per [prop. 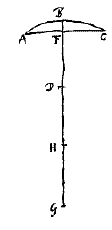 Sit nunc superficies convexa ABC radijs opposita. Si igitur axis BD producatur ad G, ut BG ad GD habeat proportionem refractionis, erit punctum G quo tendent radij post primam refractionem in superficie ABC {* Prop.
Sit nunc superficies convexa ABC radijs opposita. Si igitur axis BD producatur ad G, ut BG ad GD habeat proportionem refractionis, erit punctum G quo tendent radij post primam refractionem in superficie ABC {* Prop. 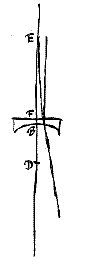
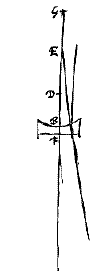 Quod si ergo superficies plana radijs advenientibus obversa est, producatur tantum DB in E, ut DE ad EB sit proportio ea quae est refractionis; eritque E punctum dispersus quaesitum, uti manifestum est ex prop. [
Quod si ergo superficies plana radijs advenientibus obversa est, producatur tantum DB in E, ut DE ad EB sit proportio ea quae est refractionis; eritque E punctum dispersus quaesitum, uti manifestum est ex prop. [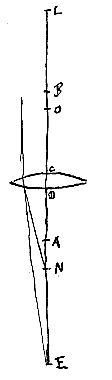
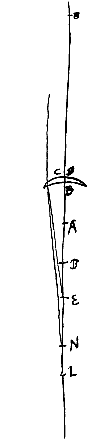 Sit lens utravis harum CD, et superficiei C centrum A, B vero superficiei D. Jungatur AB et producatur utrimque et fiat ut tam CE ad EA, quam DL ad LB rationem habeant quae est refractionis. Deinde sicut EL ad ED ita sit EB ad EN, haec autem EN in partem eam sumenda est, quam praecipit prop. [
Sit lens utravis harum CD, et superficiei C centrum A, B vero superficiei D. Jungatur AB et producatur utrimque et fiat ut tam CE ad EA, quam DL ad LB rationem habeant quae est refractionis. Deinde sicut EL ad ED ita sit EB ad EN, haec autem EN in partem eam sumenda est, quam praecipit prop. [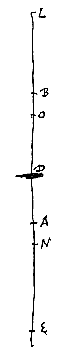
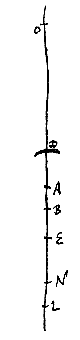 At si crassitudinem lentis CD pro nulla habeamus, uti fere semper in sequentibus fiet, dico puncta concursus parallelorum O et N aequaliter a lente remota esse. Sit enim nunc punctum medium lentis D pro utrisque D et C.
At si crassitudinem lentis CD pro nulla habeamus, uti fere semper in sequentibus fiet, dico puncta concursus parallelorum O et N aequaliter a lente remota esse. Sit enim nunc punctum medium lentis D pro utrisque D et C.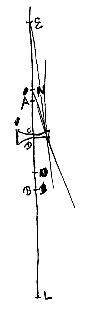
 Sit data lens CD quae superficiem utramque cavam habeat, vel alteram earum convexam, sed quae majoris sit sphaerae quam cava. Sint autem semidiametri superficierum AC, BD, quae producantur ad L et E; ut tam CE ad EA quam DL ad LB habeat proportionem quae refractionem metitur. Et ut EL ad ED ita sit EB ad EN. Dico N fore punctum dispersus radiorum qui paralleli incident a parte C.
Sit data lens CD quae superficiem utramque cavam habeat, vel alteram earum convexam, sed quae majoris sit sphaerae quam cava. Sint autem semidiametri superficierum AC, BD, quae producantur ad L et E; ut tam CE ad EA quam DL ad LB habeat proportionem quae refractionem metitur. Et ut EL ad ED ita sit EB ad EN. Dico N fore punctum dispersus radiorum qui paralleli incident a parte C.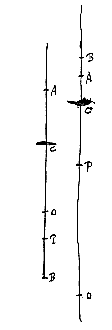 Sit lentis C superficies altera data, hoc est semidiameter ejus convexitatis AC, deturque distantia CO, oporteatque invenire superficiem alteram quae juncta priori, lentem efficiat quae radios parallelos cogat ad punctum O.
Sit lentis C superficies altera data, hoc est semidiameter ejus convexitatis AC, deturque distantia CO, oporteatque invenire superficiem alteram quae juncta priori, lentem efficiat quae radios parallelos cogat ad punctum O.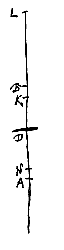
 Sit data lens D qualem diximus vel meniscus. Et centra superficierum sint A et B. Fiat ut BA ad AD ita BD ad DK*). Dico DK esse semidiametrum convexi, lentis quae alteram superficiem planam habeat, quaeque paria faciat cum lente D. Habeat enim DL ad LB proportionem quae est refractionis, et ut BA ad AD ita sit LB ad DN. Erit ergo N focus lentis D, per ea quae in prop. [
Sit data lens D qualem diximus vel meniscus. Et centra superficierum sint A et B. Fiat ut BA ad AD ita BD ad DK*). Dico DK esse semidiametrum convexi, lentis quae alteram superficiem planam habeat, quaeque paria faciat cum lente D. Habeat enim DL ad LB proportionem quae est refractionis, et ut BA ad AD ita sit LB ad DN. Erit ergo N focus lentis D, per ea quae in prop. [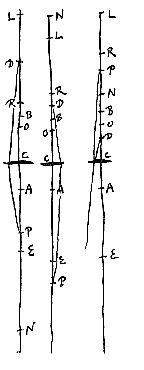
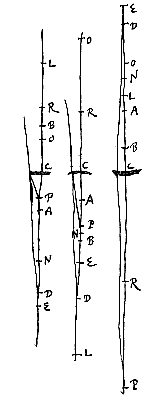 Si duabus ab eo puncto distantijs tertia proportionalis statuatur, quarum distantiarum prima sit ad punctum quo pertinent refractiones parallelorum a contraria parte incidentium, secunda ad lentem ipsam;
Si duabus ab eo puncto distantijs tertia proportionalis statuatur, quarum distantiarum prima sit ad punctum quo pertinent refractiones parallelorum a contraria parte incidentium, secunda ad lentem ipsam; 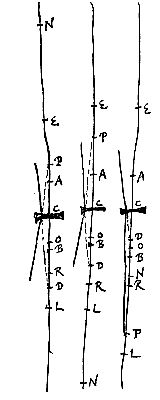 Et ponatur duabus DO, DC tertia proportionalis DP, ita ut DO, DP semper sint versus partem eandem. Dico P fore punctum concursus vel dispersus radiorum ex D vel ad D procedentium. Debet autem D non incidere in O, quia tunc radij ex D venientes refractione lentis non cogentur ad punctum, sed paralleli evadent, ut constat ex prop. ...*).
Et ponatur duabus DO, DC tertia proportionalis DP, ita ut DO, DP semper sint versus partem eandem. Dico P fore punctum concursus vel dispersus radiorum ex D vel ad D procedentium. Debet autem D non incidere in O, quia tunc radij ex D venientes refractione lentis non cogentur ad punctum, sed paralleli evadent, ut constat ex prop. ...*).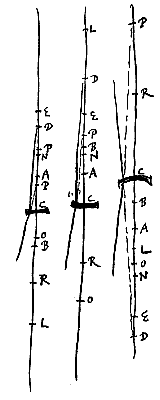 Quare et NE ad RC ut EC ad DR. Sed ut RC ad RO ita diximus esse LE ad EC. Ergo ex aequali in ratione perturbata*), erit ut EN ad RO ita LE, DR. Et permutando et invertendo, ut LE ad EN ita DR ad RO. Hinc vero et LE ad LN ut DR ad DO, ac proinde rectang. LE, DO aequale LN, DR. Est autem sicut DO ad OC ita rectang. DO, LE ad OC, LE. Ergo erit DO ad OC ut rectang. LN, DR ad OC, LE, hoc est ad rectang. LC, RC. Dictum enim fuit antea quod LE ad LC sicut CR ad CO. Est autem ut DO ad OC ita DC ad CP, quia ex constr. proportionales sunt DO, DC, DP. Ergo DC ad CP sicut rectang. LN, DR ad LC, CR. Rectangulum autem LC, CR aequale est LB, AR, quia CL ad LB ex constr. ut AR ad RC. Ergo DC ad CP rationem habet quam rectang. DR, LN ad LB, AR, hoc est, compositam ex rationibus DR ad RA et LN ad LB. Ratio autem DC ad CP componitur quoque ex rationibus DC ad CN et CN ad CP. Ergo eadem est ratio composita ex rationibus DR ad RA et LN ad LB, compositae ex rationibus DC ad CN et CN ad CP. Ratio autem DC ad CN est eadem quae DR ad RA, quia ex constr. proportionales sunt DR, DA; DC, DN. Ergo et reliqua ratio LN ad LB eadem est reliquae CN ad CP. Unde proportionales quoque erunt NL, NB; NC, NP.
Quare et NE ad RC ut EC ad DR. Sed ut RC ad RO ita diximus esse LE ad EC. Ergo ex aequali in ratione perturbata*), erit ut EN ad RO ita LE, DR. Et permutando et invertendo, ut LE ad EN ita DR ad RO. Hinc vero et LE ad LN ut DR ad DO, ac proinde rectang. LE, DO aequale LN, DR. Est autem sicut DO ad OC ita rectang. DO, LE ad OC, LE. Ergo erit DO ad OC ut rectang. LN, DR ad OC, LE, hoc est ad rectang. LC, RC. Dictum enim fuit antea quod LE ad LC sicut CR ad CO. Est autem ut DO ad OC ita DC ad CP, quia ex constr. proportionales sunt DO, DC, DP. Ergo DC ad CP sicut rectang. LN, DR ad LC, CR. Rectangulum autem LC, CR aequale est LB, AR, quia CL ad LB ex constr. ut AR ad RC. Ergo DC ad CP rationem habet quam rectang. DR, LN ad LB, AR, hoc est, compositam ex rationibus DR ad RA et LN ad LB. Ratio autem DC ad CP componitur quoque ex rationibus DC ad CN et CN ad CP. Ergo eadem est ratio composita ex rationibus DR ad RA et LN ad LB, compositae ex rationibus DC ad CN et CN ad CP. Ratio autem DC ad CN est eadem quae DR ad RA, quia ex constr. proportionales sunt DR, DA; DC, DN. Ergo et reliqua ratio LN ad LB eadem est reliquae CN ad CP. Unde proportionales quoque erunt NL, NB; NC, NP.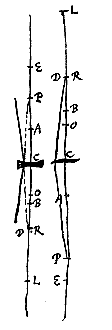 Cum vero contingit puncta D et R in unum coire, constructis caeteris ut prius, praeter punctum N, demonstratio erit hujusmodi. Nimirum quia dictum fuit esse EL ad LC ut RC ad CO, erit RO seu DO ad OC ut EC ad CL. Sicut autem DO ad OC ita est DC ad CP, et ut EC ad CL ita RC ad LB, quia ex constr. est CE ad EA sive CR ut CL ad LB. Itaque DC ad CP ut RC seu DC ad LB. ac proinde CP ipsi LB aequalis. Et addita utrique BC, erit quoque BP aequalis LC. Ergo eadem ratio BP ad LB seu PC quae CL ad LB. Haec autem est ratio refractionis ex constructione.
Cum vero contingit puncta D et R in unum coire, constructis caeteris ut prius, praeter punctum N, demonstratio erit hujusmodi. Nimirum quia dictum fuit esse EL ad LC ut RC ad CO, erit RO seu DO ad OC ut EC ad CL. Sicut autem DO ad OC ita est DC ad CP, et ut EC ad CL ita RC ad LB, quia ex constr. est CE ad EA sive CR ut CL ad LB. Itaque DC ad CP ut RC seu DC ad LB. ac proinde CP ipsi LB aequalis. Et addita utrique BC, erit quoque BP aequalis LC. Ergo eadem ratio BP ad LB seu PC quae CL ad LB. Haec autem est ratio refractionis ex constructione. 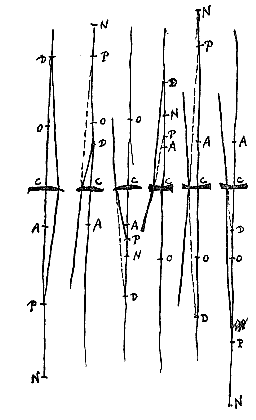
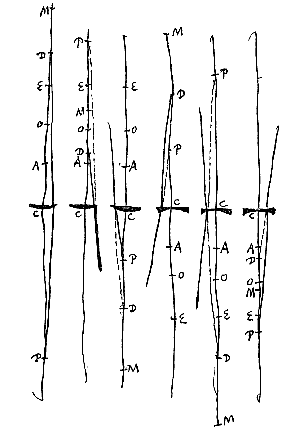 Si vero in planam lentis superficiem primum radij incidant, rursusque centrum superficiei sphaericae sit A; fiat ut CE ad EA proportionem refractionis habeat, atque item MC ad CD. Quia igitur O punctum est quo pertinent refractiones parallelorum, erit CO aequalis AE {* Prop.
Si vero in planam lentis superficiem primum radij incidant, rursusque centrum superficiei sphaericae sit A; fiat ut CE ad EA proportionem refractionis habeat, atque item MC ad CD. Quia igitur O punctum est quo pertinent refractiones parallelorum, erit CO aequalis AE {* Prop.