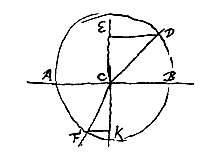 Sit liquidi vel solidi diaphani corporis versus K existentis superficies plana, quae ab alio plano, in quo figura haec descripta intelligitur, secetur secundum rectam AB. In hanc incidat radius obliquus DC, qui ad rectam ECK, superficiei propositae perpendicularem, faciat angulum DCE; is in aqua vitrove perget secundum CF minori angulo ad CK inclinatam, quam sit angulus DCE. atque ea lege ut sinus utriusque anguli, hoc est perpendiculares eorum DE, FK ex circumferentia circuli centro C descripti in rectam EK demissae certam, eandemque semper inter se rationem servent.
Sit liquidi vel solidi diaphani corporis versus K existentis superficies plana, quae ab alio plano, in quo figura haec descripta intelligitur, secetur secundum rectam AB. In hanc incidat radius obliquus DC, qui ad rectam ECK, superficiei propositae perpendicularem, faciat angulum DCE; is in aqua vitrove perget secundum CF minori angulo ad CK inclinatam, quam sit angulus DCE. atque ea lege ut sinus utriusque anguli, hoc est perpendiculares eorum DE, FK ex circumferentia circuli centro C descripti in rectam EK demissae certam, eandemque semper inter se rationem servent.
Haec autem refractionum mensura, non sinuum, sed angulorum ipsorum proportione ab Alhaseno Arabe et Vitellione°) olim definita fuerat, et experimentis quibusdam utcunque confirmata. Sed cum in majoribus radiorum inclinationibus a vero discrepare proportio illa reperiretur, diligentius sibi eandem rem recentiores investigandam existimarunt.
*) La Catoptrique d'Archimède est mentionnée par Théon d'Alexandrie [... e.a.].
[...] dans la Catoptrique dite d'Euclide, où on lit: "Si un objet est jetée dans un vase et que la distance est choisie de telle manière qu'on ne l'aperçoit plus, alors, lorsque de l'eau est versée dans le vase et que la distance reste la même, l'objet jeté dans le vase sera vu".
°) [...] Alhazen, dans l'"Opticae Thesaurus" [1572, p. 232] décrit les instruments nécessaires pour mesurer les angles d'incidence et de réfraction [...]. Vitellio (Opera [1572] X, 8) a donné des tables pour les angles de réfraction pour trois combinaisons de milieux différents, savoir air-eau, air-verre et eau-verre. [...] l'Optique de Ptolemée, ouvrage inconnu à Huygens et ses contemporains.
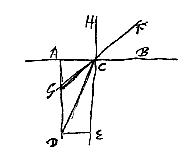 Nam positâ, ex. gratia, aquae superficie AB, visibili vero sub aqua in D, quod oculo in F posito appareat quasi in recta FC, continuabat hanc FC, donec in G puncto occurreret rectae DA, ad superficiem aquae perpendiculari; hisque ita descriptis, statuebat imaginem rei visae apparere in G, rectaeque CD ad CG certam esse rationem, veluti in aqua sesquitertiam. Quae rectarum inter se ratio vera est, ac convenit prorsus cum ea quam paulo ante explicuimus refractionis lege; quia CD est ad CG, ex doctrina triangulorum, ut sinus anguli DGC, vel AGC, seu HCF, ad sinum ang. CDG, sive DCE. Verum ad hanc sinuum proportionem nequaquam attendit Snellius et usque adeo ab apparente imagine rem omnem pendere existimavit, ut etiam in radio perpendiculari qualis HC, effectum refractionis, seu, ut falso opinatur, decurtationem radij visorij agnoscat*). deceptus eo quod etiam recta desuper in vas aqua plenum inspicienti, fundus omni parte attolli videtur. Cujus rei vera causa ex radijs ad utrumque oculum tendentibus petenda est.
Nam positâ, ex. gratia, aquae superficie AB, visibili vero sub aqua in D, quod oculo in F posito appareat quasi in recta FC, continuabat hanc FC, donec in G puncto occurreret rectae DA, ad superficiem aquae perpendiculari; hisque ita descriptis, statuebat imaginem rei visae apparere in G, rectaeque CD ad CG certam esse rationem, veluti in aqua sesquitertiam. Quae rectarum inter se ratio vera est, ac convenit prorsus cum ea quam paulo ante explicuimus refractionis lege; quia CD est ad CG, ex doctrina triangulorum, ut sinus anguli DGC, vel AGC, seu HCF, ad sinum ang. CDG, sive DCE. Verum ad hanc sinuum proportionem nequaquam attendit Snellius et usque adeo ab apparente imagine rem omnem pendere existimavit, ut etiam in radio perpendiculari qualis HC, effectum refractionis, seu, ut falso opinatur, decurtationem radij visorij agnoscat*). deceptus eo quod etiam recta desuper in vas aqua plenum inspicienti, fundus omni parte attolli videtur. Cujus rei vera causa ex radijs ad utrumque oculum tendentibus petenda est.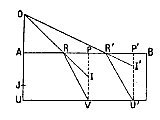 Esto medii densioris terminus AB, visibile V, radius incidentiae VR, refractus in rariore medio RO, oculi situs in puncto O. Videbitur itaque imago rei visibilis in concursu radii refracti OR continuati et perpendicularis incidentiae; qua sit VP et punctum concursus I. In eodem itaque medio, sc. hic densiore, radius incidentiae verus erit VR, suusque apparens RI. Docent observata quae ratio est VR ad RI, semper obtinere eandem inter quoscumque radios similes; ut U'R' et R'I', quin in ipso radio perpendiculari et irrefracto UA ubi incidentis ipsius pars est radius apparens; neque enim res visibilis U spectata perpendiculariter suo apparet loco, sed superiore in J: atque ut UA ad AJ, ita VR se habet ad RI.
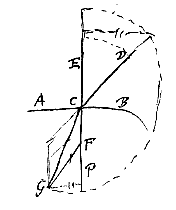
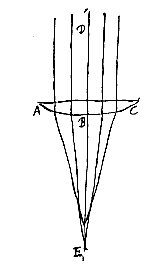
Esto medii densioris terminus AB, visibile V, radius incidentiae VR, refractus in rariore medio RO, oculi situs in puncto O. Videbitur itaque imago rei visibilis in concursu radii refracti OR continuati et perpendicularis incidentiae; qua sit VP et punctum concursus I. In eodem itaque medio, sc. hic densiore, radius incidentiae verus erit VR, suusque apparens RI. Docent observata quae ratio est VR ad RI, semper obtinere eandem inter quoscumque radios similes; ut U'R' et R'I', quin in ipso radio perpendiculari et irrefracto UA ubi incidentis ipsius pars est radius apparens; neque enim res visibilis U spectata perpendiculariter suo apparet loco, sed superiore in J: atque ut UA ad AJ, ita VR se habet ad RI. 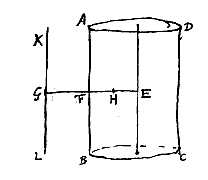 nam°) si liquida diaphani materia data sit, ea vitreum vas impleatur, quod vel cylindri formam habeat, vel ejusmodi solum quae circa axem rotunda sit; quo autem capacius erit, quoque tenuiori vitri, eo melius. Esto illud ABDC, atque ita collocetur, ut axem habeat solaribus radijs, vel ab lumine longinquo venientibus, directe oppositum. Hi igitur radij si cadant in latus DC, concurrent ex parte altera vasis, postquam et vitrum et aquam eo contentam transierint, et, si cylindraceum vas fuerit, lineam quandam lucidam signabunt ut KL in plana superficie vasis lateri parallela. Ea ubi perfectissima contigerit linea minimaeque latitudinis, circino capiatur distantia GF qua planum a vase abest, eaque distantia in chartam annotetur; atque apponatur deinde semidiameter vasis FE a centro ad extimam superficiem, quae bifariam secetur in H.
nam°) si liquida diaphani materia data sit, ea vitreum vas impleatur, quod vel cylindri formam habeat, vel ejusmodi solum quae circa axem rotunda sit; quo autem capacius erit, quoque tenuiori vitri, eo melius. Esto illud ABDC, atque ita collocetur, ut axem habeat solaribus radijs, vel ab lumine longinquo venientibus, directe oppositum. Hi igitur radij si cadant in latus DC, concurrent ex parte altera vasis, postquam et vitrum et aquam eo contentam transierint, et, si cylindraceum vas fuerit, lineam quandam lucidam signabunt ut KL in plana superficie vasis lateri parallela. Ea ubi perfectissima contigerit linea minimaeque latitudinis, circino capiatur distantia GF qua planum a vase abest, eaque distantia in chartam annotetur; atque apponatur deinde semidiameter vasis FE a centro ad extimam superficiem, quae bifariam secetur in H.
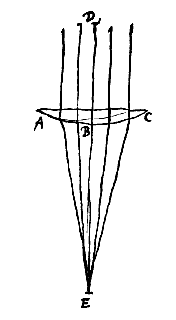 Quod si vitri aut crystalli refractiones simili compendio inquirere libeat, lentem ex ea materia formatam accipe, superficie altera plana, altera convexa, qualis hic est lens ABC. Superficiem planam soli oppone vel lucernae procul positae ut radij incidant ad rectos angulos: post lentem vero adhibe planum aliquod, ac tantum remove, ut in eo radij coeuntes imaginem solis aut flammae quam nitidissimam depingant: Esto in E. Tum distantiam hujus imaginis ab lentis convexa superficie metire EB, et quam rationem habet semidiameter convexitatis ABC puta DB una cum inventa longitudine BE, hoc est, tota DE ad hanc ipsam BE, eandem scito esse refractionis vitri vel crystalli propositae. hoc enim demonstrabitur lib. I. prop. [
Quod si vitri aut crystalli refractiones simili compendio inquirere libeat, lentem ex ea materia formatam accipe, superficie altera plana, altera convexa, qualis hic est lens ABC. Superficiem planam soli oppone vel lucernae procul positae ut radij incidant ad rectos angulos: post lentem vero adhibe planum aliquod, ac tantum remove, ut in eo radij coeuntes imaginem solis aut flammae quam nitidissimam depingant: Esto in E. Tum distantiam hujus imaginis ab lentis convexa superficie metire EB, et quam rationem habet semidiameter convexitatis ABC puta DB una cum inventa longitudine BE, hoc est, tota DE ad hanc ipsam BE, eandem scito esse refractionis vitri vel crystalli propositae. hoc enim demonstrabitur lib. I. prop. [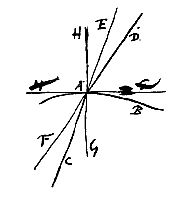
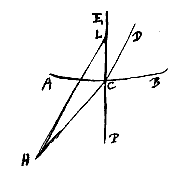
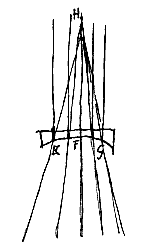 Similiterque in lente cava KFG, si parallelos radios a parte H venientes post refractionem ita spargi ostenderimus, ut retrorsum producti conveniant cum axe FH omnes citra punctum quoddam H, vel omnes ultra, ijsdemque etiam conditionibus quas in convexa posuimus, tum punctum H dicetur punctum dispersus. Quin etiam haec puncta plerumque sic accipiemus, tanquam concursum aut dispersum radiorum exacte determinarent; medias videlicet lentium aut superficierum partes respicientes, quarum satis exigua sit proportio ad convexitatis vel cavitatis diametros, ut quantum ad sensum oculorum attinet perfectum videatur quod geometrica ratione est imperfectum. Ita enim sese habere lentium latitudines certum est, tum earum quibus in tenebris picturam representari videmus rerum quae foris a Sole illuminantur, tum quibus perspicilla seu telescopia constant; neque enim alioqui tam insignes earum effectus cernerentur.
Similiterque in lente cava KFG, si parallelos radios a parte H venientes post refractionem ita spargi ostenderimus, ut retrorsum producti conveniant cum axe FH omnes citra punctum quoddam H, vel omnes ultra, ijsdemque etiam conditionibus quas in convexa posuimus, tum punctum H dicetur punctum dispersus. Quin etiam haec puncta plerumque sic accipiemus, tanquam concursum aut dispersum radiorum exacte determinarent; medias videlicet lentium aut superficierum partes respicientes, quarum satis exigua sit proportio ad convexitatis vel cavitatis diametros, ut quantum ad sensum oculorum attinet perfectum videatur quod geometrica ratione est imperfectum. Ita enim sese habere lentium latitudines certum est, tum earum quibus in tenebris picturam representari videmus rerum quae foris a Sole illuminantur, tum quibus perspicilla seu telescopia constant; neque enim alioqui tam insignes earum effectus cernerentur.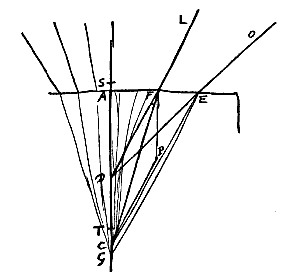 Dico T fore punctum concursus quaesitum. Et primo quidem ostendam nullius radij refractionem concurrere cum AD citra punctum T. Sit enim FC refractio radij LF; et perficiatur parallelogrammum CDFP. Erit igitur FP superficiei AE ad angulos rectos, et PC parallela radio LF, ejusque refractioni occurrens in C. Quare FC ad CP habebit proportionem quae est refractionis {* Prop.
Dico T fore punctum concursus quaesitum. Et primo quidem ostendam nullius radij refractionem concurrere cum AD citra punctum T. Sit enim FC refractio radij LF; et perficiatur parallelogrammum CDFP. Erit igitur FP superficiei AE ad angulos rectos, et PC parallela radio LF, ejusque refractioni occurrens in C. Quare FC ad CP habebit proportionem quae est refractionis {* Prop. 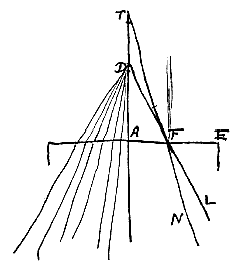 Dico T fore punctum dispersus quaesitum: Hoc est radiorum ex D procedentium refractiones, sicut FN est radij DF, intra diaphanum ita ferri, quasi venirent ex puncto T.
Dico T fore punctum dispersus quaesitum: Hoc est radiorum ex D procedentium refractiones, sicut FN est radij DF, intra diaphanum ita ferri, quasi venirent ex puncto T.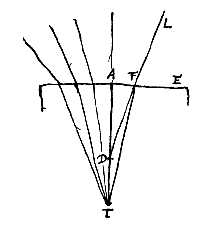 Sit plana superficies diaphani AE et punctum T datum, ex quo radij ad superficiem AE ferantur ut TF. Sit TA recta ad superficiem AE perpendicularis, eaque dividatur in D ita ut TA ad DA habeat proportionem refractionis. Dico D fore punctum dispersus quaesitum: ut nempe FL refractio radij TF feratur quasi ex puncto D procederet. Jungatur enim FD. Si igitur LF esset radius incidens in superficiem AE, tendensque ad punctum D, ejus refractio foret FT, ut ex probl.
Sit plana superficies diaphani AE et punctum T datum, ex quo radij ad superficiem AE ferantur ut TF. Sit TA recta ad superficiem AE perpendicularis, eaque dividatur in D ita ut TA ad DA habeat proportionem refractionis. Dico D fore punctum dispersus quaesitum: ut nempe FL refractio radij TF feratur quasi ex puncto D procederet. Jungatur enim FD. Si igitur LF esset radius incidens in superficiem AE, tendensque ad punctum D, ejus refractio foret FT, ut ex probl.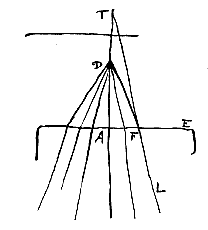
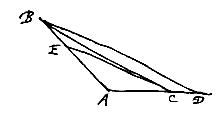 Sit enim ducta CE parallela DB. Quoniam ergo angulus A obtusus est; angulus autem BEC aequalis utrisque simul, angulo A et ECA: Erit et BEC angulus obtusus, ideoque in triangulo BEC latus BC major latere EC. quare minor ratio erit EC ad CA quam BC ad CA. ut autem EC ad CA ita BD ad DA. Ergo minor quoque ratio BD ad DA quam BC ad CA. Quod erat propositum.
Sit enim ducta CE parallela DB. Quoniam ergo angulus A obtusus est; angulus autem BEC aequalis utrisque simul, angulo A et ECA: Erit et BEC angulus obtusus, ideoque in triangulo BEC latus BC major latere EC. quare minor ratio erit EC ad CA quam BC ad CA. ut autem EC ad CA ita BD ad DA. Ergo minor quoque ratio BD ad DA quam BC ad CA. Quod erat propositum.
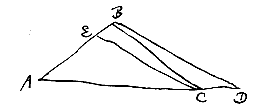 Sit enim CE parallela DB. Quoniam ergo trianguli CBE obtusus est angulus B, Erit latus CE majus latere CB: ac proinde minor ratio AC ad CE quam AC ad CB. Ut autem AC ad CE ita est AD ad DB. Ergo minor quoque ratio AD ad DB quam AC ad CB. quod erat propositum.
Sit enim CE parallela DB. Quoniam ergo trianguli CBE obtusus est angulus B, Erit latus CE majus latere CB: ac proinde minor ratio AC ad CE quam AC ad CB. Ut autem AC ad CE ita est AD ad DB. Ergo minor quoque ratio AD ad DB quam AC ad CB. quod erat propositum.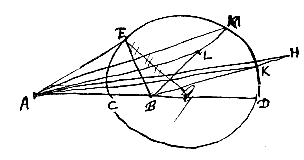
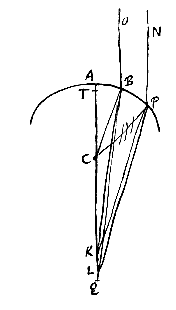 Esto superficies convexa diaphani ABP cujus centrum C, in quam incidant radij ut OB, NP, paralleli rectae AC quae per centrum ducta est. Producatur AC usque in Q, ut AQ ad QC habeat rationem eam quae est refractionis. Dico Q fore punctum concursus quaesitum.
Esto superficies convexa diaphani ABP cujus centrum C, in quam incidant radij ut OB, NP, paralleli rectae AC quae per centrum ducta est. Producatur AC usque in Q, ut AQ ad QC habeat rationem eam quae est refractionis. Dico Q fore punctum concursus quaesitum.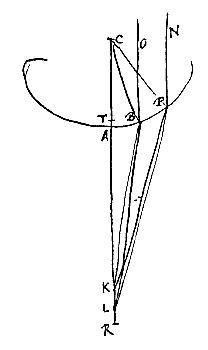 Sit superficies convexa AB, centro C, per quod ducta sit CA radijs incidentibus parallela. Producatur ea ad R, et habeat CR ad RA proportionem refractionis. Dico R esse punctum concursus quaesitum.
Sit superficies convexa AB, centro C, per quod ducta sit CA radijs incidentibus parallela. Producatur ea ad R, et habeat CR ad RA proportionem refractionis. Dico R esse punctum concursus quaesitum.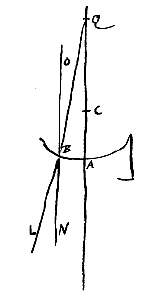 Sit superficies cava AB ex sphaera cujus centrum C, incidantque in eam radij rectae CA paralleli ut OB. Producatur AC, et habeat AQ ad QC proportionem eam quae est refractionis. Dico Q esse punctum dispersus quaesitum: hoc est, radios ita refractione inflecti ut pergant tanquam ex puncto Q promanantes.
Sit superficies cava AB ex sphaera cujus centrum C, incidantque in eam radij rectae CA paralleli ut OB. Producatur AC, et habeat AQ ad QC proportionem eam quae est refractionis. Dico Q esse punctum dispersus quaesitum: hoc est, radios ita refractione inflecti ut pergant tanquam ex puncto Q promanantes.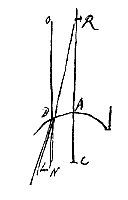 Ad superficiem cavam AB cujus centrum C, accidant radij paralleli rectae AC, ut OB. Producatur CA, et habeat CR ad RA proportionem refractionis. Dico R esse punctum dispersus quaesitum.
Ad superficiem cavam AB cujus centrum C, accidant radij paralleli rectae AC, ut OB. Producatur CA, et habeat CR ad RA proportionem refractionis. Dico R esse punctum dispersus quaesitum.