I   (1652)   Cet Appendice contient le début du manuscrit de la Dioptrique, tel qu'il était vers 1666, lors que la copie de Niquet fut prise. Il constitue probablement la leçon primitive, précédée peut-être d'un mot au lecteur ou préface [...]. 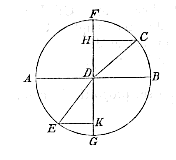  Quando ex aere in vitrum, aut lapides diaphanos radius lucis incidit, aut in aquam aliosve liquores transparantes, docuit experientia hoc modo refractionem fieri. Sit exempli gratia aquae superficies plana AB, in quam cadat radius CD, in aere existens: Sit autem ducta per D punctum perpendicularis ad dictam superficiem, recta FDG, et centro D scribatur circulus CFE. Radius igitur CD, cum ad perpendicularem inclinatur angulo FDC, idem vitro feretur secundum rectam DE, ita ut minorem angulum cum eadem perpendiculari constituat EDG.   Sinus vero anguli FDC, qui est CH, ad sinum anguli EDG nempe EK, certam quandam proportionem servat: quae in omni inclinatione eadem perpetuo invenitur [<]. Et in aqua quidem haec proportio proxime est sesquitertia; ut nempe CH sit partium quatuor qualium EK est trium.

[ 144 ]

[ v ]

In vitro autem et crystallo circiter sesquialtera. Nec accurate ea definiri in universum potest, cum nec in vitro omni, nec in omni aqua, praecise eadem sit [>]. Sed proposita quaevis materia pellucida quaenam in eo sit Refractionis proportio, ita enim deinceps eam vocabimus, inquirere licebit methodo aliqua earum quas paulo post adferemus [<].   Rursus vero cum ex vitro aut aqua, similive corpore refractionem faciente, radius lucidus egreditur, contrario modo is inflectitur, sed nihilo magis minusve quam in ingressu; velut quia radij CD refractio intra aquam est secundum DE, hinc vice versa si radius ED occurrat intrinsecus eidem aquae superficiei AB incedet refractus secundum DC.   Haec autem ita se habere plurimorum experimentis et observationibus accuratissimis compertum est: Imo eorum quoque qui hanc refractionum legem necdum intelligebant. Ita enim a Keplero, cum angulus CDH est maximum omnium qui esse possunt, hoc est gr. 90° vel potius tantillo minor, invenitur angulus EDK, gr. 42, quod jam dictis plane consonum est, quia nempe ut 3 ad 2, quam diximus esse proportionem refractionis vitri, ita est quam proxime sinus gr. 90 hoc est 100000 ad sinum gr. 42, hoc est, 66913. Quod vero angulo CDH, 30 gradibus minore existente, definit angulum EDK duabus tertijs ipsius CDH aequalem, ne in hoc quidem male nobiscum convenit, quando quidem in angulis qui 30 gradibus minores sint, eadem proxime sinuum inter se atque ipsorum angulorum ratio est.

[ 145 ]

[ v ]

Porro ad rationem inquirendae refractionum mensurae seu proportionis, quod attinet, quoniam complures eam non una via tradiderunt ut Cartesius, Keplerus, alijque, sufficeret fortasse si ab ijs peti juberem; neque etiam difficile fuerit ijs qui praecedentia intellexerint, nova ad hoc artificia excogitare. Verum tamen quia minimo negotio, et satis accurate sequentibus modis investigari potest, operae praetium erit hic eos adscribere. Ergo si liquida quavis materia data sit ... [<]

[ 154 ]

[ v ]

III   1658   3 Maj. 1658.  5 pomerid.   Angulus exploratus semidiametri primae iridis in sphaera crystallina, fuit in prima observatione   18.55' in 2da.   18.20' in 3a.   18.10' in 4a.   18.32' unde vero proximum puto   18.22'  circiter.   paulo adhuc minores anguli. quia aliquid perdimus de altitudine solis dum illa posterior observatur. 6' vel 7'. sit ergo 18.16.   At in vitro veneto erat 22.0'. Ergo diversa aliquantum refractio crystalli reperitur ac vitri.

[ 155 ]

[ v ]

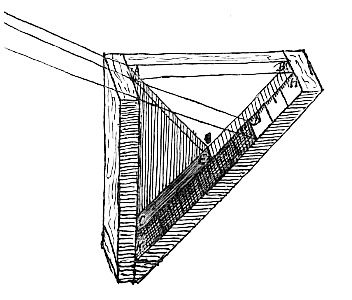
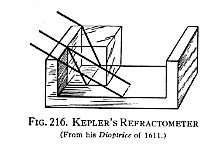AB est latus superius trianguli vitrei, ligno inclusi, lateri maximo BC charta alba glutine affigenda. Angulus ad A rectus accurate formandus. Latus AB diversimode ad solem inclinatur. AD est radius rectus AE radius refractus.   Charta HK divisiones habet graduum.     [ Lloyd W. Taylor, Physics. The pioneer science (1941, Dover). J. Kepler, Dioptrice, p. 1.]

[ 156 ]

[ v ]

V   1664   d. ven[eris]. 19 Sept. 1664.   Vase vitreo aqua pleno, investigavi proportionem refractionis aquae quae fuit ea quae lineae AB ad BC [<]. Ex fossa hausta erat. Eâdem sale saturatâ pauxillo major inventa est refractionis proportio, nempe quae AD ad DC. Est autem ratio AB ad BC paulo major quam 4 ad 3, hoc est quam AE ad EC.

[ AB = 14 cm ]

I   (1652)   Cet Appendice nous fait connaître la rédaction primitive du début du deuxième Livre [<], telle qu'on la retrouve aux p. 42 et 43 de la copie de Niquet. Propositio   Per foramen minimum intuenti, quae prius vel ratione distantiae, vel ob interpositas lentes, confusa cernebantur, distincta apparebunt, etsi minus lucida; quae vero distincta cernebantur ita videri perseverabunt, eademque qua prius magnitudine ac situ.   Manifestum est ex superioribus confusam visionem non aliunde fieri quam quod radij ab uno visibilis rei puncto ad oculum feruntur, sive simpliciter id fiat, sive trajectis quibusvis lentibus, ad unum rursus retiformis punctum non conveniant, sed alij alio loco sistantur. Quod si jam pupilla eousque arctari intelligatur, ut quasi unius puncti rationem habeat; vel si lamina minimo foramine pertusa ante oculum apponatur, liquet hoc pacto tantum uni veluti radiorum, qui a singulis punctis innumeri alioqui ad pupillam feruntur, transitum concedi, qui proinde in uno tantum retiformis puncto locum ejus unde emissus est puncti signare queat. Ex quo distincta visio sequatur necesse est. Minus lucidam vero fore hinc manifestum est, quod cum antea tot radij, quod a visibilis puncto pupillam intrabant, ejus puncti imaginem in fundo oculi illustrarent, nunc paucissimus ac veluti unus tantum eorum radiorum oculum ingrediatur.

[ 236 ]

[ v ]

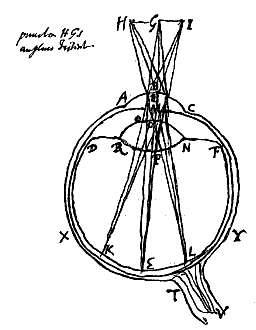Ad alteram porro propositionis partem demonstrandam repetatur figura ad oculi explicationem superius descripta [<]. Quum igitur distincta visio ponatur fieri, ad quam requiritur ut radij omnes qui a punctis singulis rei visae, ut H, G, I, ad oculum promanant, sive per aerem tantum, sive per quaslibet lentes transierint, ad totidem rursus puncta in fundo oculi colligantur, ut L, E, K; clarum est, quod si opposito ad oculum exili foramine, tantum unus veluti a singulis punctis radius admittatur, is nihilominus eodem quo prius loco in fundum oculi incidens, punctum unde effluxit, etsi minus dilucide, ibi pinget. Quare nec magnitudinem nec situm rei visae quicquam immutatum iri constat, sed eodem modo sese habitura atque antea cum sine interposita lamina libere ad oculum radij deferebantur.   Quando igitur in sequentibus ad ineundam apparentis ac verae magnitudinis rationem, instar puncti oculum esse statuemus recte procedere eas demonstrationes ex his manifestum erit, cum nihil intersit, quantum ad perceptarum imaginum magnitudinem an ad puncti exilitatem oculi apertura reducta sit an tota, ut solet, pateat.   Quando autem apparentem rei trans lentes visae magnitudinem ijs quoque casibus definivisse inveniemus, quibus distincta visio non contingit, tum quod primo loco hic ostensum fuit, in mentem revocetur, nempe confusam visionem semper emendari posse, contracta uti dictum est oculi apertura. Quamvis et lente insuper aliqua, cava vel convexa, oculo proxime admota, confusionem ab alijs lentibus ortam, tolli. [Prop. II]