Et invertendo ratio DA ad AL minor compositâ ex rationibus DC ad CL et AR ad RC; hoc est, ratione rectanguli DC, AR ad rectangulum CL, CR, hoc est, ratione DQ ad QL. Quare et dividendo ratio DL ad LA minor erit ratione DL ad LQ. Unde patet LQ minorem esse quam LA. Est autem ratio DC ad CL major quam DQ ad QL, nam DC ad CL ratio major est quam rectanguli DC, AR, ad rectangulum CL, CR, quia AR minor est quam CR. Itaque patet punctum Q cadere inter A et C.
Jam porro dividatur DK in V, ut habeat DV ad VK rationem eam quam rectangulum DC, AR ad rectangulum KC, CR. Haec autem est majoris ad minus, siquidem hoc eadem ratione ostenditur qua supra ostensum fuit rectangulum DC, AR majus esse rectangulo LC, CR. Deinde fiat ut DV ad VK ita DX ad XK, cadetque punctum X inter A et C, aeque ac punctum Q, nam hoc similiter quoque demonstrari potest. Sit autem circuli cirumferentia circa XV diametrum descripta. Ea secabit circulum AP in ipso puncto P ubi radius GP convexo AB occurrere dictus est.
Producatur enim PK, et occurrat ei CN parallela GPD. Ergo quia PK posita est esse refractio radij GP, cui parallela ex centro ducta est CN, habebit PN ad NC rationem refractionis. Est igitur CN ad NP ut AR ad RC. Unde sic porro argumentabimur. Ratio CN ad NK componitur ex rationibus CN ad NP et NP ad NK, hoc est, et DC ad CK; igitur ratio CN ad NK, hoc est, DP ad PK, componitur ex rationibus AR ad RC et DC ad CK, ex quibus componitur quoque ratio rectanguli AR, DC ad rectangulum RC, CK. Igitur DP ad PK erit ut rectangulum AR, DC ad rectangulum RC, CK. ac proinde etiam sicut DV ad VK, nec non ut DX ad XK. Quare circumferentia cujus diameter XV, transibit per punctum P {* Lem. 5}, ut dicebamus.
Jam quia ratio DT ad TL est eadem quae rectanguli AR, DC ad rectangulum RC, CL; ratio vero DV ad VK eadem quae rectanguli AR, DC ad rectangulum RC, CK; minor erit ratio DT ad TL quam DV ad VK, quia rectang. RC, CL majus est rectangulo RC, CK. Itaque multo minor ratio DT ad TK quam DV ad VK; nam DK major est posita quam DL. Apparet igitur punctum T cadere inter D et V. Punctum vero Q dico cadere inter A et X.
Sit enim ut DQ ad QL ita DX ad XY. Ergo quia XK ad XD per constr. ut rectang. RC, CK ad rectangulum AR, DC; DX autem ad XY ut DQ ad QL, hoc est ut rectang. AR, DC ad rectangulum RC, CL: erit ex aequo XK ad XY ut rectang. RC, CK ad rectang. RC, CL, hoc est, ut CK ad CL. Et XK ad KY ut CK ad KL. Est autem XK major quam CK, ut superius dictum fuit. Ergo KY major quoque quam KL, ideoque DY minor quam DL. Erat autem DX ad XY ut DQ ad QL, et per conversionem rationis DX ad DY ut DQ ad DL. Ergo quum DY sit minor quam DL, erit et DX minor quam DQ. Unde necessario punctum Q cadet inter A et X, nam quod inter A et C cadat jam ante ostensum fuit. Sed punctum T ostendimus distare ab A ultra punctum V. Ergo manifestum est circumferentiam QBT secare circulum APH inter A et P. Quod demonstrandum supererat.
|
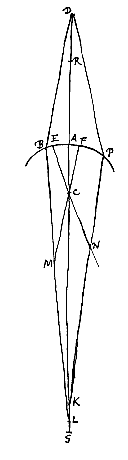 Cum superficies est convexa, et a puncto venientes radij extrinsecus in eam deferuntur.
Cum superficies est convexa, et a puncto venientes radij extrinsecus in eam deferuntur. 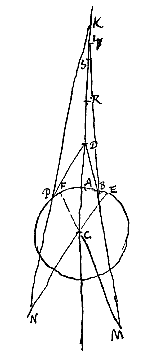 Esto autem nunc punctum D inter A et R datum; et fiat rursus ut DR ad DA ita DC ad DS; accipiatur autem DS non versus C sed versus R. Dico radios ex puncto D in superficiem AB incidentes post refractionem ita inflecti quasi venirent ex puncto S, sive S fore punctum dispersus radiorum refractorum.
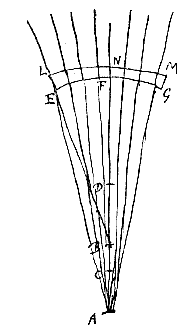
Esto autem nunc punctum D inter A et R datum; et fiat rursus ut DR ad DA ita DC ad DS; accipiatur autem DS non versus C sed versus R. Dico radios ex puncto D in superficiem AB incidentes post refractionem ita inflecti quasi venirent ex puncto S, sive S fore punctum dispersus radiorum refractorum.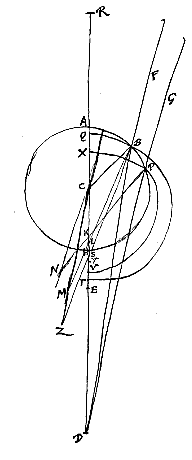 Esto data convexa diaphani superficies AB, et punctum D, quo tendentes radij ut FB, GP, exterius incidant in dictam superficiem. Centrum autem convexitatis sit C, per quod ducta sit recta DCA. Producatur DA, et habeat CR ad RA proportionem refractionis. Erit ergo R concursus parallelorum a contraria parte venientium.
Esto data convexa diaphani superficies AB, et punctum D, quo tendentes radij ut FB, GP, exterius incidant in dictam superficiem. Centrum autem convexitatis sit C, per quod ducta sit recta DCA. Producatur DA, et habeat CR ad RA proportionem refractionis. Erit ergo R concursus parallelorum a contraria parte venientium.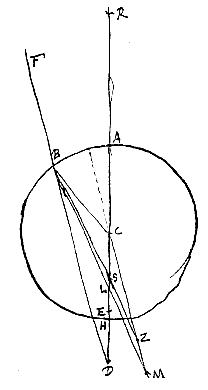
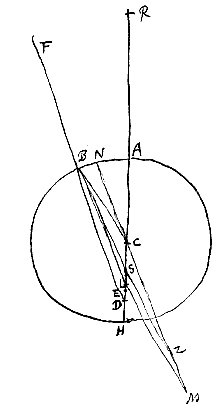 Porro simile fere demonstratione, atque in casu primo [
Porro simile fere demonstratione, atque in casu primo [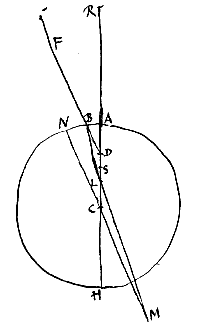
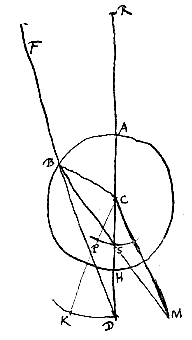
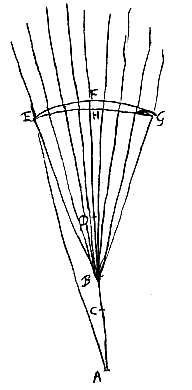
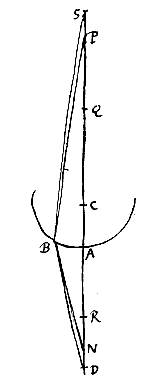 Sit convexa diaphani superficies AB et punctum S, ex quo in illam perveniant radij ut SB, qui quidem egredientes diaphanum refringentur, nisi S sit idem cum convexi centro C. Est autem praeterea quoque duplex casus. Junctâ enim SC, eademque productâ, ac circumferentiam AB secante in A, si fecerimus ut AQ ad QC habeat rationem quae est refractionis, erit punctum S vel propius puncto A quam punctum Q, vel ulterius remotum. Nam si convenit cum puncto Q, perspicuum est ex propos.
Sit convexa diaphani superficies AB et punctum S, ex quo in illam perveniant radij ut SB, qui quidem egredientes diaphanum refringentur, nisi S sit idem cum convexi centro C. Est autem praeterea quoque duplex casus. Junctâ enim SC, eademque productâ, ac circumferentiam AB secante in A, si fecerimus ut AQ ad QC habeat rationem quae est refractionis, erit punctum S vel propius puncto A quam punctum Q, vel ulterius remotum. Nam si convenit cum puncto Q, perspicuum est ex propos. 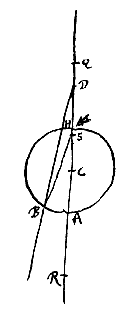 Sit nunc punctum S datum, ut minus distet ab A quam punctum Q. Erit autem vel inter Q et C vel inter C et A. nam cum in C incidit nullam fieri refractionem jam diximus. Sit primo inter Q et C punctum S; et fiat rursus ut SQ ad SA ita SC ad SD quae sumatur in partem a centro C aversam. Dico D fore punctum dispersus radiorum refractorum qui ab S puncto egrediuntur. Sumatur enim, ut ante, AR aequalis CQ. Erit ergo et CR ad RA proportio refractionis, eadem nempe quae AQ ad QC. Et quoniam SQ ad SA ut SC ad SD, erit et componendo QA, hoc est, RC ad AS ut CD ad DS. quare et utraque simul RC, CD hoc est DR ad utramque simul AS, DS, hoc est ad DA ut DC ad DS. Ergo radiorum ad D tendentium et in convexa superficie AB refractorum punctum concursus erit S {* Pars
Sit nunc punctum S datum, ut minus distet ab A quam punctum Q. Erit autem vel inter Q et C vel inter C et A. nam cum in C incidit nullam fieri refractionem jam diximus. Sit primo inter Q et C punctum S; et fiat rursus ut SQ ad SA ita SC ad SD quae sumatur in partem a centro C aversam. Dico D fore punctum dispersus radiorum refractorum qui ab S puncto egrediuntur. Sumatur enim, ut ante, AR aequalis CQ. Erit ergo et CR ad RA proportio refractionis, eadem nempe quae AQ ad QC. Et quoniam SQ ad SA ut SC ad SD, erit et componendo QA, hoc est, RC ad AS ut CD ad DS. quare et utraque simul RC, CD hoc est DR ad utramque simul AS, DS, hoc est ad DA ut DC ad DS. Ergo radiorum ad D tendentium et in convexa superficie AB refractorum punctum concursus erit S {* Pars 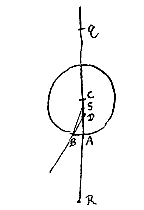
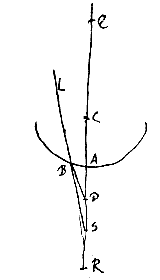 Esto diaphani convexa superficies AB, et datum punctum S, quo tendant radij, ut LB intrinsecus superficiei occurrentes, centrum vero convexi sit C. Jungatur SC secetque superficiem in A, et producatur ad Q, ut AQ ad QC habeat proportionem refractionis; et ut SQ ad SA ita sit SC ad SD. Dico D esse punctum concursus radiorum refractorum qui ad S punctum pergunt. Sit enim AR aequalis CQ; ergo et CR ad RA habebit proportionem refractionis. Et quia SQ ad SA ut SC ad SD, erit dividendo, QA, hoc est, CR ad SA ut CD ad DS. Quare auferendo CD a CR, et DS ab SA, erit et reliqua DR ad reliquam DA ut DC ad DS.
Esto diaphani convexa superficies AB, et datum punctum S, quo tendant radij, ut LB intrinsecus superficiei occurrentes, centrum vero convexi sit C. Jungatur SC secetque superficiem in A, et producatur ad Q, ut AQ ad QC habeat proportionem refractionis; et ut SQ ad SA ita sit SC ad SD. Dico D esse punctum concursus radiorum refractorum qui ad S punctum pergunt. Sit enim AR aequalis CQ; ergo et CR ad RA habebit proportionem refractionis. Et quia SQ ad SA ut SC ad SD, erit dividendo, QA, hoc est, CR ad SA ut CD ad DS. Quare auferendo CD a CR, et DS ab SA, erit et reliqua DR ad reliquam DA ut DC ad DS.
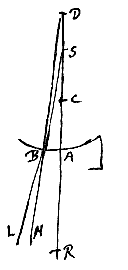
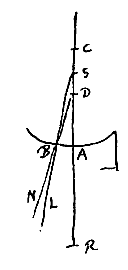 Sit superficies sphaerica cava AB cujus centrum C, incidantque in eam radij a puncto dato D procedentes, ut DB. Jungatur DC, et producta secet superficiem in A, et habeat CR ad RA proportionem refractionis. Erit ergo R punctum dispersus radiorum parallelorum ab opposita parte venientium. Jam sicut DR ad DA ita sit DC ad DS. Dico S fore punctum dispersus radiorum ex D egredientium postquam in superficie AB refracti fuerint.
Sit superficies sphaerica cava AB cujus centrum C, incidantque in eam radij a puncto dato D procedentes, ut DB. Jungatur DC, et producta secet superficiem in A, et habeat CR ad RA proportionem refractionis. Erit ergo R punctum dispersus radiorum parallelorum ab opposita parte venientium. Jam sicut DR ad DA ita sit DC ad DS. Dico S fore punctum dispersus radiorum ex D egredientium postquam in superficie AB refracti fuerint.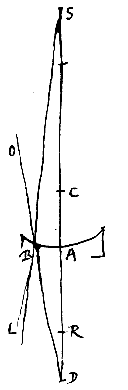 Sit superficies sphaerica cava AB, centro C; incidantque in eam radij ad punctum datum D tendentes, ut OB. Agatur recta per DC, secans superficiem in A, et habeat CR ad RA proportionem refractionis. Et ut DR ad DA ita sit DC ad DS. Dico priore casu, cum R cadit inter A, D, punctum S fore punctum dispersus radiorum qui ad D tendebant.
Sit superficies sphaerica cava AB, centro C; incidantque in eam radij ad punctum datum D tendentes, ut OB. Agatur recta per DC, secans superficiem in A, et habeat CR ad RA proportionem refractionis. Et ut DR ad DA ita sit DC ad DS. Dico priore casu, cum R cadit inter A, D, punctum S fore punctum dispersus radiorum qui ad D tendebant.
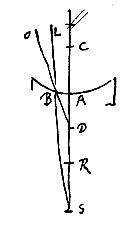 Altero vero casu, cum D cadit inter A, R, eventurum contra ut S sit punctum eorum concursus. Si autem D fuerit idem quod punctum R, radij eo tendentes, post refractionem fient inter se et axi AC paralleli, ut in propos. [
Altero vero casu, cum D cadit inter A, R, eventurum contra ut S sit punctum eorum concursus. Si autem D fuerit idem quod punctum R, radij eo tendentes, post refractionem fient inter se et axi AC paralleli, ut in propos. [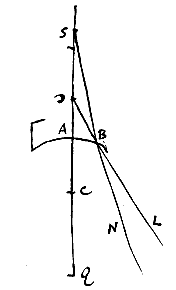 Sit superficies cava AB, cujus centrum C; et punctum S, unde digressi radij ut SB intrinsecus in superficiem ferantur.
Sit superficies cava AB, cujus centrum C; et punctum S, unde digressi radij ut SB intrinsecus in superficiem ferantur.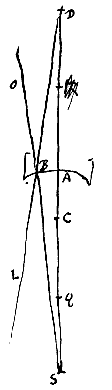
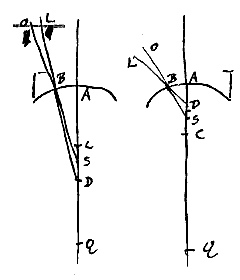 Sit diaphani cava superficies AB; centrum ejus C; et punctum datum sit S quo tendentes radij ut OB, intrinsecus dictae superficiei occurrant. Ducatur recta per C, secans superficiem in A, habeatque AQ ad QC proportionem refractionis. Porro ut SQ ad SA ita sit SC ad SD.
Sit diaphani cava superficies AB; centrum ejus C; et punctum datum sit S quo tendentes radij ut OB, intrinsecus dictae superficiei occurrant. Ducatur recta per C, secans superficiem in A, habeatque AQ ad QC proportionem refractionis. Porro ut SQ ad SA ita sit SC ad SD.