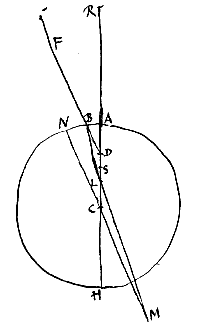
Laat nu het punt D gegeven zijn tussen A en C, en ook hier zal van straal FB de gebrokene BL tussen D en C vallen. Ik zeg dat het punt van samenkomst L hier weer verder van A af ligt dan punt S. Trek BL door, en laat CM (evenwijdig aan FBD) hem in M ontmoeten. Omdat dus punt D op de diameter ligt tussen A en het middelpunt C, zal DB groter zijn da DA. Maar CM is kleiner dan AR, zoals vaststaat uit voorstel VIII, omdat CM evenwijdig is aan straal FB, waarvan BM de gebrokene is. Dus is de verhouding BD tot CM, dat is DL tot LC, groter dan DA tot AR. En zoals DA tot AR, zo is DS tot SC. Dus de verhouding DL tot LC is groter dan DS tot SC; en door samenstelling, DC tot CL is groter dan DC tot CS. Dus is CL kleiner dan CS. Waaruit voortvloeit dat punt L verder dan S van A af ligt.
En verder is, op dezelfde manier als in het voorgaande geval, aan te tonen dat ook hier van sommige stralen de gebrokenen dichter bij punt S samenkomen dan een willekeurig gegeven afstand. Dus zal S ook hier het punt van samenkomst zijn van de stralen die naar D gericht zijn.
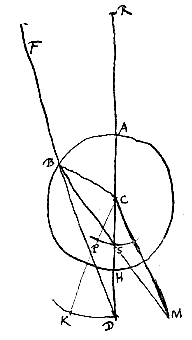 Het laatste geval is nog over om te bewijzen*), waarbij punt D buiten de bol ABH gelegen is, zodanig dat DC tot CH dezelfde verhouding heeft als CR tot RA, d.w.z. de brekingsverhouding. We hebben gezegd [<] dat in dit geval van alle stralen die naar D gericht zijn de gebrokenen precies in punt S verzameld worden, dat namelijk gevonden wordt door te maken dat DR : DA = DC : DS.
Het laatste geval is nog over om te bewijzen*), waarbij punt D buiten de bol ABH gelegen is, zodanig dat DC tot CH dezelfde verhouding heeft als CR tot RA, d.w.z. de brekingsverhouding. We hebben gezegd [<] dat in dit geval van alle stralen die naar D gericht zijn de gebrokenen precies in punt S verzameld worden, dat namelijk gevonden wordt door te maken dat DR : DA = DC : DS.
Als punt D ligt zoals gezegd is, beschouwen we een willekeurige straal FBD die daarop gericht is, en vanaf het punt van samenkomst B trekken we naar punt S de rechte BS. Ik zeg dat de gebrokene van straal FB deze BS zelf is. Want we trekken BS door, tot hij CM ontmoet, die evenwijdig is aan FBD, en we verbinden B met C.
Omdat dus DC tot CH of CA is, zoals CR tot RA, zal ook de hele DR tot RC zijn als CR tot RA. Verder is DR : RC = DA : AS, omdat namelijk door constructie geldt DR : DA = DC : DS. Dus is ook DA : AS = CR : RA, dat is DC : CH. Dus als van DA afgetrokken wordt DC, en van AS wordt afgetrokken CH of CA, zal ook de rest CA, of CH, tot de rest CS dezelfde verhouding hebben als DC tot CH.
Verder is CB gelijk aan CH. Dus is ook BC : CS = DC : CB. En daarom zijn de driehoeken DCB en BCS gelijkvormig, aangezien ze ook de hoek bij C gemeenschappelijk hebben, die door de evenredige zijden wordt ingesloten. Dan zal ook de derde zijde DB van de ene driehoek tot de derde zijde BS van de andere, de verhouding hebben van DC tot CB of CH; en hoek SBC zal gelijk zijn aan hoek BDC.
Hieruit volgt nu dus dat in de driehoeken DBS en BMC, de hoek MBC gelijk is aan de hoek BDS. Verder is ook hoek BMC gelijk aan hoek DBS, wegens de evenwijdigheid van BD en CM. Dus zullen de genoemde driehoeken DBS en BMC ook gelijkvormig zijn, en daarom is BM tot MC als DB tot BS, d.w.z. als DC tot CH, d.w.z. als CR tot RA. Daarom heeft BM tot MC een verhouding die gelijk is aan de brekingsverhouding. En CM is evenwijdig met de straal FB. Dus is BSM de gebrokene van straal FB {* voorstel II}; wat aangetoond moest worden.
Alle stralen dus die naar D gericht zijn, en het bolle oppervlak AB ontmoeten, komen na de breking samen in één enkel punt S.
[ *) Wat volgt wordt in een brief aan R. F. de Sluse (T. 2, p. 67) genoemd: "een zeer kort bewijs".]
|
 Stel dat van een doorschijnend lichaam het oppervlak AB bolvormig en bol is, met middelpunt C, en dat D een punt is vanwaar stralen komen die daarop terechtkomen, zoals DB. We trekken een rechte door D en C, en geven daarop een punt aan, zodanig dat CR tot RA de brekingsverhouding heeft. Dan is R het punt van samenkomst van evenwijdige stralen die van de andere kant komen {* voorstel IX}.
Stel dat van een doorschijnend lichaam het oppervlak AB bolvormig en bol is, met middelpunt C, en dat D een punt is vanwaar stralen komen die daarop terechtkomen, zoals DB. We trekken een rechte door D en C, en geven daarop een punt aan, zodanig dat CR tot RA de brekingsverhouding heeft. Dan is R het punt van samenkomst van evenwijdige stralen die van de andere kant komen {* voorstel IX}. 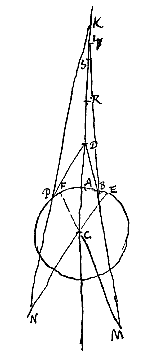 Laat daarentegen nu het punt D tussen A en R gegeven zijn; en zorg er weer voor dat zoals DR tot DA, zo DC tot DS is; doch DS wordt niet in de richting van C genomen, maar in de richting van R. Ik zeg dat stralen uit punt D die op het oppervlak AB invallen na de breking zo afgebogen worden alsof ze kwamen uit punt S, oftewel dat S het spreidingspunt van de gebroken stralen is.
Laat daarentegen nu het punt D tussen A en R gegeven zijn; en zorg er weer voor dat zoals DR tot DA, zo DC tot DS is; doch DS wordt niet in de richting van C genomen, maar in de richting van R. Ik zeg dat stralen uit punt D die op het oppervlak AB invallen na de breking zo afgebogen worden alsof ze kwamen uit punt S, oftewel dat S het spreidingspunt van de gebroken stralen is.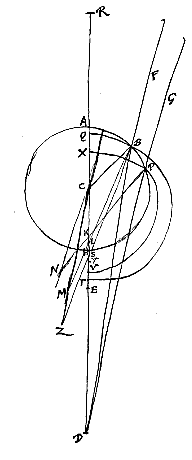 Laat het bolle oppervlak AB van een doorschijnend lichaam gegeven zijn, en het punt D, waarop gericht zijn stralen zoals FB en GP, die van buiten invallen op genoemd oppervlak. En het middelpunt van de bolling is C, waardoor de rechte DCA getrokken wordt. DA wordt verlengd, en CR heeft tot RA de brekingsverhouding. Dus zal R het punt van samenkomst zijn van evenwijdige stralen die van de andere kant komen.
Laat het bolle oppervlak AB van een doorschijnend lichaam gegeven zijn, en het punt D, waarop gericht zijn stralen zoals FB en GP, die van buiten invallen op genoemd oppervlak. En het middelpunt van de bolling is C, waardoor de rechte DCA getrokken wordt. DA wordt verlengd, en CR heeft tot RA de brekingsverhouding. Dus zal R het punt van samenkomst zijn van evenwijdige stralen die van de andere kant komen.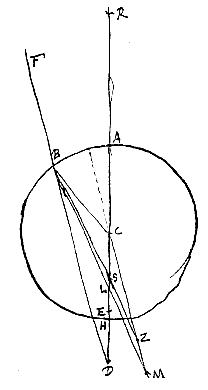 Laat nu de verhouding van DC tot CH kleiner zijn dan de brekingsverhouding, dat is die van CR tot RA, en het punt D hetzij buiten de cirkel ABH, hetzij erbinnen, maar zodanig dat het verder van A af ligt dan het middelpunt C. Want wanneer het tussen A en C geplaatst is, is er nog een bijzonder geval, dat we later zullen bezien. Als dus de straal FB gericht is naar punt D, en gebroken samenkomt met de as AC in punt L, zeg ik dat L verder van A ligt dan punt S.
Laat nu de verhouding van DC tot CH kleiner zijn dan de brekingsverhouding, dat is die van CR tot RA, en het punt D hetzij buiten de cirkel ABH, hetzij erbinnen, maar zodanig dat het verder van A af ligt dan het middelpunt C. Want wanneer het tussen A en C geplaatst is, is er nog een bijzonder geval, dat we later zullen bezien. Als dus de straal FB gericht is naar punt D, en gebroken samenkomt met de as AC in punt L, zeg ik dat L verder van A ligt dan punt S.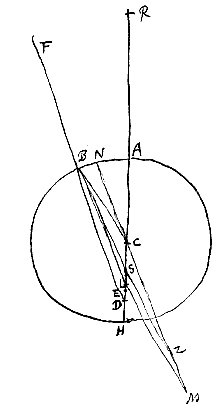 Verder kan, met een bijna gelijk bewijs als in het eerste geval [
Verder kan, met een bijna gelijk bewijs als in het eerste geval [

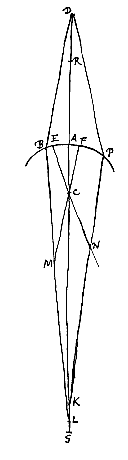
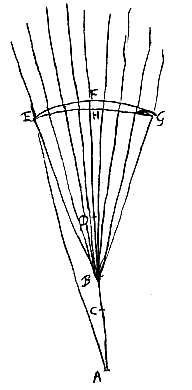 Verder zullen we met behulp hiervan, aangezien we nu ook grondige kennis hebben van de breking van glas, en een bolvormig oppervlak makkelijk is te polijsten, lenzen kunnen maken die stralen, die naar een gegeven punt gericht zijn, in een ander gegeven punt laten samenkomen. Evenzo lenzen die stralen, die uit een gegeven punt komen, zo afbuigen alsof ze uit een ander gegeven punt voortkomen.
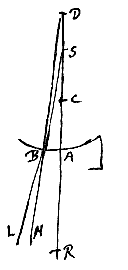
Verder zullen we met behulp hiervan, aangezien we nu ook grondige kennis hebben van de breking van glas, en een bolvormig oppervlak makkelijk is te polijsten, lenzen kunnen maken die stralen, die naar een gegeven punt gericht zijn, in een ander gegeven punt laten samenkomen. Evenzo lenzen die stralen, die uit een gegeven punt komen, zo afbuigen alsof ze uit een ander gegeven punt voortkomen. 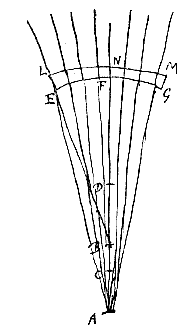 Evenzo, als gegeven zijn de punten A en B, en gevonden de cirkelomtrek EFG (zoals we gezegd hebben), en als een andere cirkelomtrek LNM beschreven wordt met middelpunt B, maar met een straal BN die wat groter is dan BF: de vorm ELNMGF zal de doorsnede van de andere lens weergeven, die bewerkt dat stralen in de richting van punt B, worden gericht naar A.
Evenzo, als gegeven zijn de punten A en B, en gevonden de cirkelomtrek EFG (zoals we gezegd hebben), en als een andere cirkelomtrek LNM beschreven wordt met middelpunt B, maar met een straal BN die wat groter is dan BF: de vorm ELNMGF zal de doorsnede van de andere lens weergeven, die bewerkt dat stralen in de richting van punt B, worden gericht naar A. 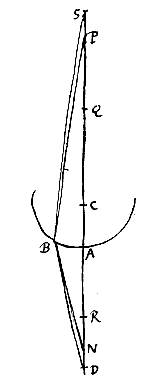 Gegeven het bolle oppervlak AB van een doorschijnend lichaam, en een punt S, waaruit stralen komen die het oppervlak bereiken, zoals SB, en die wel gebroken zullen worden als ze uit het doorschijnende gaan, tenzij S hetzelfde punt is als het middelpunt C van de bolling. Verder zijn er bovendien ook twee gevallen.
Gegeven het bolle oppervlak AB van een doorschijnend lichaam, en een punt S, waaruit stralen komen die het oppervlak bereiken, zoals SB, en die wel gebroken zullen worden als ze uit het doorschijnende gaan, tenzij S hetzelfde punt is als het middelpunt C van de bolling. Verder zijn er bovendien ook twee gevallen. 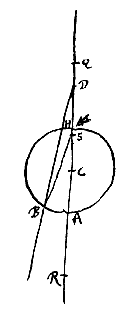 Laat nu het punt S zo gegeven zijn, dat het minder ver van A af ligt dan het punt Q. Dan zal het ofwel tussen Q en C liggen, ofwel tussen C en A; want wanneer het samenvalt met C zal er zoals gezegd geen breking zijn. Neem eerst aan dat punt S tussen Q en C ligt; en maak weer SQ : SA = SC : SD, met de laatste aan de kant die van het middelpunt C afgekeerd is. Ik zeg dat D het spreidingspunt zal zijn van de gebrokenen van de stralen die uit punt S weggaan.
Laat nu het punt S zo gegeven zijn, dat het minder ver van A af ligt dan het punt Q. Dan zal het ofwel tussen Q en C liggen, ofwel tussen C en A; want wanneer het samenvalt met C zal er zoals gezegd geen breking zijn. Neem eerst aan dat punt S tussen Q en C ligt; en maak weer SQ : SA = SC : SD, met de laatste aan de kant die van het middelpunt C afgekeerd is. Ik zeg dat D het spreidingspunt zal zijn van de gebrokenen van de stralen die uit punt S weggaan. 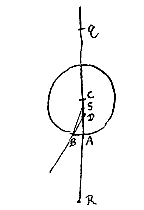 Dat geval tenslotte waarin punt S tussen A en C gegeven is, wordt op dezelfde manier geconstrueerd als het laatst voorafgaande, en heeft een bewijs dat er op lijkt. Daar namelijk SQ : SA = SC : SD, zal door samenstelling gelden QA (of RC) : AS = CD : DS. En daarom, door CD af te trekken van RC, en DS van AS, zal ook de rest DR tot de rest DA zijn als DC tot DS. Waaruit we op dezelfde manier het overige zullen besluiten. Het punt D zal dan het spreidingspunt zijn, op zo'n manier dat alle gebrokenen, na verlenging achterwaarts, vóór dit punt samenkomen, d.w.z. tussen D en A.
Dat geval tenslotte waarin punt S tussen A en C gegeven is, wordt op dezelfde manier geconstrueerd als het laatst voorafgaande, en heeft een bewijs dat er op lijkt. Daar namelijk SQ : SA = SC : SD, zal door samenstelling gelden QA (of RC) : AS = CD : DS. En daarom, door CD af te trekken van RC, en DS van AS, zal ook de rest DR tot de rest DA zijn als DC tot DS. Waaruit we op dezelfde manier het overige zullen besluiten. Het punt D zal dan het spreidingspunt zijn, op zo'n manier dat alle gebrokenen, na verlenging achterwaarts, vóór dit punt samenkomen, d.w.z. tussen D en A.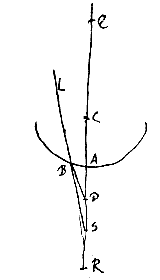 Het bolle oppervlak van een doorschijnend lichaam is AB, en het gegeven punt S, waarheen stralen gericht zijn zoals LB, het oppervlak aan de buitenkant ontmoetend, en het bollingsmiddelpunt is C. We verbinden S met C en deze snijdt het oppervlak in A, en hij wordt verlengd naar Q, zodanig dat AQ tot QC de brekingsverhouding heeft; en SQ : SA = SC : SD. Ik zeg dat D het punt van samenkomst is van de gebrokenen van stralen die naar punt S gaan. Want neem AQ gelijk aan CQ; dan zal ook CR tot RA de brekingsverhouding hebben. En omdat SQ : SA = SC : SD, zal door verdeling gelden QA (of CR) : SA = CD : DS. En daarom, door CD van CR af te trekken, en DS van SA, zal ook de rest DR tot de rest DA zijn als DC tot DS.
Het bolle oppervlak van een doorschijnend lichaam is AB, en het gegeven punt S, waarheen stralen gericht zijn zoals LB, het oppervlak aan de buitenkant ontmoetend, en het bollingsmiddelpunt is C. We verbinden S met C en deze snijdt het oppervlak in A, en hij wordt verlengd naar Q, zodanig dat AQ tot QC de brekingsverhouding heeft; en SQ : SA = SC : SD. Ik zeg dat D het punt van samenkomst is van de gebrokenen van stralen die naar punt S gaan. Want neem AQ gelijk aan CQ; dan zal ook CR tot RA de brekingsverhouding hebben. En omdat SQ : SA = SC : SD, zal door verdeling gelden QA (of CR) : SA = CD : DS. En daarom, door CD van CR af te trekken, en DS van SA, zal ook de rest DR tot de rest DA zijn als DC tot DS.
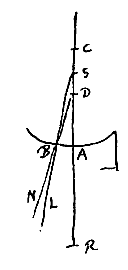 Het holle bolvormige oppervlak is AB, met middelpunt C, en er vallen stralen op die van het gegeven punt D komen, zoals DB. Verbind D met C, en het verlengde snijdt het oppervlak in A, en CR tot RA heeft de brekingsverhouding. Dan zal R het spreidingspunt zijn van evenwijdige stralen die van de andere kant komen. Verder is DR : DA = DC : DS. Ik zeg dat S het spreidingspunt zal zijn van de stralen die uit D weggaan, nadat ze gebroken zijn aan het oppervlak AB.
Het holle bolvormige oppervlak is AB, met middelpunt C, en er vallen stralen op die van het gegeven punt D komen, zoals DB. Verbind D met C, en het verlengde snijdt het oppervlak in A, en CR tot RA heeft de brekingsverhouding. Dan zal R het spreidingspunt zijn van evenwijdige stralen die van de andere kant komen. Verder is DR : DA = DC : DS. Ik zeg dat S het spreidingspunt zal zijn van de stralen die uit D weggaan, nadat ze gebroken zijn aan het oppervlak AB.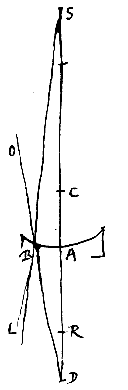 Het holle bolvormige oppervlak is AB, het middelpunt C; en er vallen stralen op die gericht zijn naar punt D, zoals OB. Er wordt een rechte getrokken langs DC, die het oppervlak in A snijdt, en CR heeft tot RA de brekingsverhouding. En DR : DA = DC : DS. Ik zeg dat in het eerste geval, wanneer R valt tussen A en D, het punt S spreidingspunt zal zijn van de stralen die naar D gericht waren.
Het holle bolvormige oppervlak is AB, het middelpunt C; en er vallen stralen op die gericht zijn naar punt D, zoals OB. Er wordt een rechte getrokken langs DC, die het oppervlak in A snijdt, en CR heeft tot RA de brekingsverhouding. En DR : DA = DC : DS. Ik zeg dat in het eerste geval, wanneer R valt tussen A en D, het punt S spreidingspunt zal zijn van de stralen die naar D gericht waren.
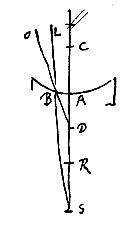 Maar in het andere geval, wanneer D valt tussen A en R, zal daarentegen de uitkomst zijn dat S hun punt van samenkomst is. En als D hetzelfde is als punt R, worden de stralen die er naartoe gericht zijn, na de breking onderling en met de as AC evenwijdig, zoals opgemerkt is in de voorstellen
Maar in het andere geval, wanneer D valt tussen A en R, zal daarentegen de uitkomst zijn dat S hun punt van samenkomst is. En als D hetzelfde is als punt R, worden de stralen die er naartoe gericht zijn, na de breking onderling en met de as AC evenwijdig, zoals opgemerkt is in de voorstellen 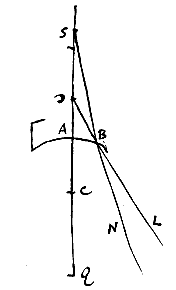 Het holle oppervlak is AB, met middelpunt C; en het punt is S, waar vandaan stralen zoals SB weggegaan zijn die van binnen tegen het oppervlak komen.
Het holle oppervlak is AB, met middelpunt C; en het punt is S, waar vandaan stralen zoals SB weggegaan zijn die van binnen tegen het oppervlak komen.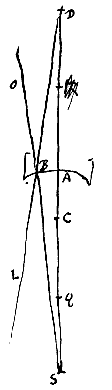
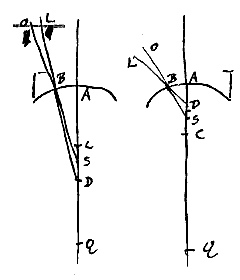 Het holle oppervlak van het doorschijnend lichaam is AB, het middelpunt ervan C; en het gegeven punt is S, waarop stralen gericht zijn, zoals OB, die van binnen het genoemde oppervlak ontmoeten. We trekken een rechte door C, die het oppervlak snijdt in A. En we geven AQ tot QC de brekingsverhouding. Verder is SQ : SA = SC : SD.
Het holle oppervlak van het doorschijnend lichaam is AB, het middelpunt ervan C; en het gegeven punt is S, waarop stralen gericht zijn, zoals OB, die van binnen het genoemde oppervlak ontmoeten. We trekken een rechte door C, die het oppervlak snijdt in A. En we geven AQ tot QC de brekingsverhouding. Verder is SQ : SA = SC : SD.