|
Nu is rechthoek LC.AE gelijk aan rechthoek LE.CO, omdat LE : EA = LC : CO; en rechthoek DE.LB is gelijk aan rechthoek EL.DN, omdat EL : LB = ED : DN. Dus is rechth. LE.CO groter dan rechthoek LE.DN, en daarom is CO groter dan DN.
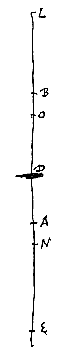
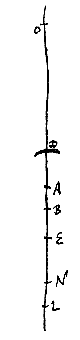 Maar als we de dikte CD van de lens verwaarlozen, zoals in het volgende bijna altijd zal gebeuren, zeg ik dat de punten van samenkomst der evenwijdige stralen, O en N, even ver van de lens liggen. Want we nemen nu het middelste punt D van de lens, in plaats van beide punten D en C.
Maar als we de dikte CD van de lens verwaarlozen, zoals in het volgende bijna altijd zal gebeuren, zeg ik dat de punten van samenkomst der evenwijdige stralen, O en N, even ver van de lens liggen. Want we nemen nu het middelste punt D van de lens, in plaats van beide punten D en C.
Omdat dus LE : LA = LD : LO, is ook LE : EA = LD : DO, waaruit volgt dat rechth. LE.DO gelijk is aan rechthoek EA.LD. En hieraan is gelijk recht. DE.LB, omdat DE : EA = DL : LB, en anderzijds is DE.LB gelijk aan rechth. EL.DN, omdat EL : LB = ED : DN. Dus kan rechth. LE.DO gelijkgesteld worden met rechthoek EL.DN; en dus DO met DN; wat te bewijzen was.
Nu is het mogelijk de punten O en N te vinden op een gemakkelijker manier. En inderdaad behoeft alleen het punt L gevonden te worden zoals eerst, namelijk door te maken dat DL : LB de brekingsverhouding is; en vervolgens dat BA : AD = LB : DN of DO*).
Want omdat DL : LB = DE : EA, zal door omzetting van de verhouding gelden LD : DB = ED : DA, en door verwisseling LD : DE = BD : DA. En daarom is ook LE : ED = BA : AD. En zoals BA : AD is, zo hebben we LB : DN gemaakt. Dus LE : ED = LB : DN. en door verwisseling, EL : LB = ED : DN. Vandaar EL : EB = ED : EN, en dus is N het gevraagde punt van samenkomst; want dit is eerder aangetoond.
Dus geldt in een glazen lens: zoals de som van de halve bollingsdiameters — maar bij de maansikkel hun verschil — tot één van beide, zo is het dubbele van de andere tot de brandpuntsafstand. Want dan wordt LB tweemaal de straal BD, omdat DL : LB = 3 : 2, wat bij glas de brekingsverhouding is. En in het geval dat beide oppervlakken even bol zijn, blijkt nu de brandpuntsafstand gelijk te zijn aan de halve bollingsdiameter.
*) Deze constructie geeft de formules f = R1 R2 / (n – 1) (R1 ± R2)
Voorstel XVII
Gegeven een holle lens met twee bolvormige oppervlakken, te vinden het spreidingspunt van evenwijdige stralen.
|
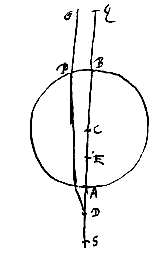 Gegeven een bol met middelpunt C en as BA, een doorsnede door het middelpunt is de cirkel BPA. En er vallen stralen op, evenwijdig met de as BA, zoals OP. De halve diameter CA wordt doormidden gedeeld in E, en verlengd; en CD : DE is de brekingsverhouding, namelijk die, welke overeenkomt met het materiaal waarvan de bol gemaakt is. Bijvoorbeeld wanneer het een kristallijnen of glazen bol is, moet de verhouding CD : DE ongeveer anderhalf zijn, en vierderde als het water is. Ik zeg dat D het gevraagde punt van samenkomst zal zijn*).
Gegeven een bol met middelpunt C en as BA, een doorsnede door het middelpunt is de cirkel BPA. En er vallen stralen op, evenwijdig met de as BA, zoals OP. De halve diameter CA wordt doormidden gedeeld in E, en verlengd; en CD : DE is de brekingsverhouding, namelijk die, welke overeenkomt met het materiaal waarvan de bol gemaakt is. Bijvoorbeeld wanneer het een kristallijnen of glazen bol is, moet de verhouding CD : DE ongeveer anderhalf zijn, en vierderde als het water is. Ik zeg dat D het gevraagde punt van samenkomst zal zijn*).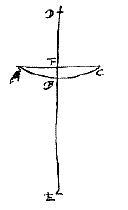 Gegeven een lens met een bol oppervlak ABC, deel van een bol met middelpunt D. En het vlakke oppervlak is AFC. En dit ligt eerst tegenover de evenwijdige stralen. We trekken de rechte DBE, die de as van de lens aangeeft, d.w.z. die het oppervlak AFC snijdt onder een rechte hoek, en we trekken deze door tot E, zodanig dat DE tot EB de brekingsverhouding heeft, die steeds als gegeven wordt beschouwd. Het is duidelijk dat E het gevraagde punt van samenkomst zal zijn*).
Gegeven een lens met een bol oppervlak ABC, deel van een bol met middelpunt D. En het vlakke oppervlak is AFC. En dit ligt eerst tegenover de evenwijdige stralen. We trekken de rechte DBE, die de as van de lens aangeeft, d.w.z. die het oppervlak AFC snijdt onder een rechte hoek, en we trekken deze door tot E, zodanig dat DE tot EB de brekingsverhouding heeft, die steeds als gegeven wordt beschouwd. Het is duidelijk dat E het gevraagde punt van samenkomst zal zijn*). 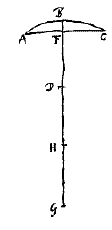 Stel nu dat het bolle oppervlak ABC tegenover de stralen ligt. Als dan de as BD verlengd wordt tot G, zodanig dat BG tot GD de brekingsverhouding heeft, zal G het punt zijn waarnaar de stralen gericht zijn na de eerste breking, aan oppervlak ABC {* voorstel
Stel nu dat het bolle oppervlak ABC tegenover de stralen ligt. Als dan de as BD verlengd wordt tot G, zodanig dat BG tot GD de brekingsverhouding heeft, zal G het punt zijn waarnaar de stralen gericht zijn na de eerste breking, aan oppervlak ABC {* voorstel 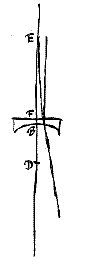
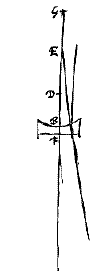 Als dan het platte oppervlak naar de aankomende stralen gekeerd is, verlengen we slechts DB naar E, zodat DE tot EB de verhouding van de breking is; en E zal het gevraagde spreidingspunt zijn, zoals duidelijk is uit voorstel
Als dan het platte oppervlak naar de aankomende stralen gekeerd is, verlengen we slechts DB naar E, zodat DE tot EB de verhouding van de breking is; en E zal het gevraagde spreidingspunt zijn, zoals duidelijk is uit voorstel 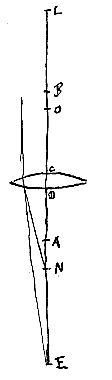
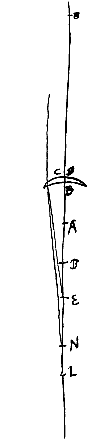 Gegeven een van deze beide lenzen, met van oppervlak C het middelpunt A, en B van oppervlak D. Verbind A met B en verleng de lijn aan weerskanten, en maak het zo dat zowel CE tot EA, als DL tot LB, een verhouding heeft gelijk aan die van de breking. Vervolgens dat EL : ED = EB : EN, en deze EN moet genomen worden aan de kant, die voorstel
Gegeven een van deze beide lenzen, met van oppervlak C het middelpunt A, en B van oppervlak D. Verbind A met B en verleng de lijn aan weerskanten, en maak het zo dat zowel CE tot EA, als DL tot LB, een verhouding heeft gelijk aan die van de breking. Vervolgens dat EL : ED = EB : EN, en deze EN moet genomen worden aan de kant, die voorstel 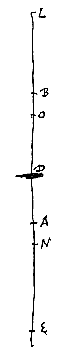
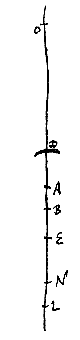 Maar als we de dikte CD van de lens verwaarlozen, zoals in het volgende bijna altijd zal gebeuren, zeg ik dat de punten van samenkomst der evenwijdige stralen, O en N, even ver van de lens liggen. Want we nemen nu het middelste punt D van de lens, in plaats van beide punten D en C.
Maar als we de dikte CD van de lens verwaarlozen, zoals in het volgende bijna altijd zal gebeuren, zeg ik dat de punten van samenkomst der evenwijdige stralen, O en N, even ver van de lens liggen. Want we nemen nu het middelste punt D van de lens, in plaats van beide punten D en C.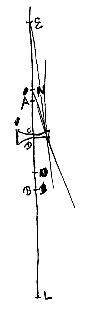
 De gegeven lens is CD, met beide oppervlakken hol, of met één ervan bol, maar dan als gedeelte van een grotere bol dan het holle oppervlak. De halve middellijnen van de oppervlakken zijn AC en BD, die verlengd worden naar L en E; zodanig dat zowel CE : EA als DL : LB de verhouding heeft waarmee de breking gemeten wordt. En EL : ED = EB : EN. Ik zeg dat N het spreidingspunt zal zijn van stralen die evenwijdig invallen aan de kant van C.
De gegeven lens is CD, met beide oppervlakken hol, of met één ervan bol, maar dan als gedeelte van een grotere bol dan het holle oppervlak. De halve middellijnen van de oppervlakken zijn AC en BD, die verlengd worden naar L en E; zodanig dat zowel CE : EA als DL : LB de verhouding heeft waarmee de breking gemeten wordt. En EL : ED = EB : EN. Ik zeg dat N het spreidingspunt zal zijn van stralen die evenwijdig invallen aan de kant van C.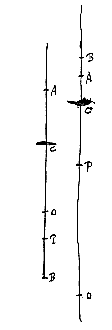 Stel dat van lens C het ene oppervlak gegeven is, d.w.z. de halve bollingsdiameter AC daarvan, en dat de afstand CO gegeven wordt, en dat gevonden moet worden een ander oppervlak, dat gevoegd bij het eerste een lens maakt, die evenwijdige stralen naar punt O brengt.
Stel dat van lens C het ene oppervlak gegeven is, d.w.z. de halve bollingsdiameter AC daarvan, en dat de afstand CO gegeven wordt, en dat gevonden moet worden een ander oppervlak, dat gevoegd bij het eerste een lens maakt, die evenwijdige stralen naar punt O brengt.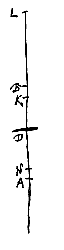
 De gegeven lens D is zoals we gezegd hebben, of een maansikkel. En de middelpunten van de oppervlakken zijn A en B. We maken BA : AD = BD : DK*). Ik zeg dat DK de halve bollingsdiameter is van een lens die het andere oppervlak plat heeft, en die hetzelfde doet als lens D.
De gegeven lens D is zoals we gezegd hebben, of een maansikkel. En de middelpunten van de oppervlakken zijn A en B. We maken BA : AD = BD : DK*). Ik zeg dat DK de halve bollingsdiameter is van een lens die het andere oppervlak plat heeft, en die hetzelfde doet als lens D. 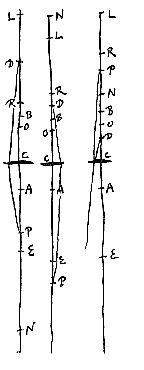
 Als met twee afstanden tot dit punt een derde evenredige vastgesteld wordt, waarbij de eerste afstand is tot het punt waarmee de evenwijdige stralen corresponderen die van de andere kant op de lens vallen, en de tweede tot de lens zelf;
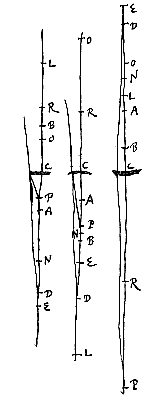
Als met twee afstanden tot dit punt een derde evenredige vastgesteld wordt, waarbij de eerste afstand is tot het punt waarmee de evenwijdige stralen corresponderen die van de andere kant op de lens vallen, en de tweede tot de lens zelf;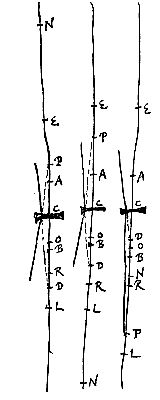 En we stellen bij de twee afstanden DO en DC een derde evenredige DP, zodanig dat DO en DP altijd aan dezelfde kant liggen. Ik zeg dat P zal zijn het punt van samenkomst of het spreidingspunt van stralen die uit D komen of naar D gaan. Maar D mag niet samenvallen met O, omdat stralen die uit D komen dan niet door de breking van de lens naar een punt gebracht worden, maar evenwijdig verder gaan, zoals vaststaat uit voorstel ...*).
En we stellen bij de twee afstanden DO en DC een derde evenredige DP, zodanig dat DO en DP altijd aan dezelfde kant liggen. Ik zeg dat P zal zijn het punt van samenkomst of het spreidingspunt van stralen die uit D komen of naar D gaan. Maar D mag niet samenvallen met O, omdat stralen die uit D komen dan niet door de breking van de lens naar een punt gebracht worden, maar evenwijdig verder gaan, zoals vaststaat uit voorstel ...*).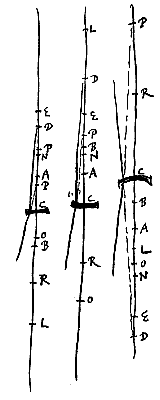 Daarom is ook NE : RC als EC : DR. Maar zoals RC : RO is, zo hebben we gezegd dat LE : EC is. Dus door gelijken in een verstoorde verhouding*), zal gelden EN : RO = LE : DR. En door verwisseling en omkering LE : EN = DR : RO. Hieruit volgt ook LE : LN = DR : DO, en dus is de rechthoek LE.DO gelijk aan LN.DR. Nu is DO : OC = DO.LE : OC.LE. Dus is DO : OC = LN.DR : OC.LE (of LC.RC). Want eerder was gezegd LE : LC = CR : CO.
Daarom is ook NE : RC als EC : DR. Maar zoals RC : RO is, zo hebben we gezegd dat LE : EC is. Dus door gelijken in een verstoorde verhouding*), zal gelden EN : RO = LE : DR. En door verwisseling en omkering LE : EN = DR : RO. Hieruit volgt ook LE : LN = DR : DO, en dus is de rechthoek LE.DO gelijk aan LN.DR. Nu is DO : OC = DO.LE : OC.LE. Dus is DO : OC = LN.DR : OC.LE (of LC.RC). Want eerder was gezegd LE : LC = CR : CO. 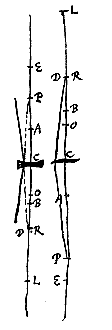 Maar wanneer het gebeurt dat de punten D en R samenvallen in één punt, zal, met het andere geconstrueerd zoals eerst, behalve punt N, het bewijs als volgt worden.
Maar wanneer het gebeurt dat de punten D en R samenvallen in één punt, zal, met het andere geconstrueerd zoals eerst, behalve punt N, het bewijs als volgt worden. 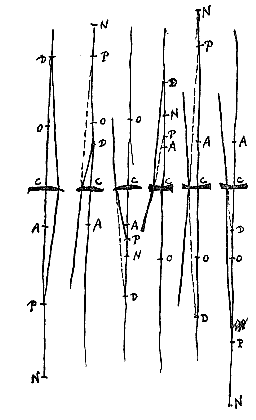
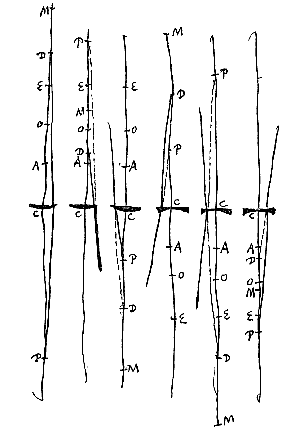 Als echter de stralen eerst invallen op het platte lensoppervlak, en als weer het middelpunt van het bolvormige oppervlak A is, maken we dat CE tot EA de brekingsverhouding heeft, en evenzo MC tot CD. Omdat dus O een punt is waarmee evenwijdige stralen corresponderen, zal CO gelijk zijn aan AE {* voorstel
Als echter de stralen eerst invallen op het platte lensoppervlak, en als weer het middelpunt van het bolvormige oppervlak A is, maken we dat CE tot EA de brekingsverhouding heeft, en evenzo MC tot CD. Omdat dus O een punt is waarmee evenwijdige stralen corresponderen, zal CO gelijk zijn aan AE {* voorstel