 Maar bij dezelfde lens, andersom geplaatst (zodat namelijk het holle oppervlak KBC de evenwijdige stralen opvangt), zijn er twee brekingen. Want straal HC wordt eerst gebroken in C, en loopt vandaar langs Cκ, die achterwaarts verlengd met de as samenkomt in P, en weer uit het platte oppervlak komend in κ gaat hij verder langs κL, die achterwaarts verlengd met de as samenkomt voor P, neem aan in D. Nu is de afstand BE van het spreidingspunt bij de lens in deze stand weer het dubbele van BA. En de aberratie ED van de uiterste straal wordt gevonden op de volgende manier.
Maar bij dezelfde lens, andersom geplaatst (zodat namelijk het holle oppervlak KBC de evenwijdige stralen opvangt), zijn er twee brekingen. Want straal HC wordt eerst gebroken in C, en loopt vandaar langs Cκ, die achterwaarts verlengd met de as samenkomt in P, en weer uit het platte oppervlak komend in κ gaat hij verder langs κL, die achterwaarts verlengd met de as samenkomt voor P, neem aan in D. Nu is de afstand BE van het spreidingspunt bij de lens in deze stand weer het dubbele van BA. En de aberratie ED van de uiterste straal wordt gevonden op de volgende manier.
Ten eerste valt de gebrokene van straal HC die behoort bij het holle oppervlak KBC (en wel Cκ) op dezelfde rechte als de gebrokene van de met de as evenwijdige straal OC, wanneer het oppervlak CBK bol zou zijn. Zodat het interval AP — waarmee het punt van samenkomst van de verlengde Cκ verwijderd is van het middelpunt A — gevonden wordt op dezelfde manier als boven bij de platbolle lens [<]; en hier is weer AP : PC = 2 : 3. Dus is ook PC bekend. Verder geldt GP : PC = BP : Pκ. Dus is ook deze bekend, en uit dezelfde gelijkvormigheid van driehoeken is ook Bκ te geven.
En daar nu bij de tweede breking de straal Cκ zo afgebogen wordt tot κL, dat, als deze met de as samenkomt in D, de verhouding Pκ : κD gelijk is aan die welke de breking bepaalt (namelijk 3 : 2), en daar Pκ bekend is, is ook κD te geven. En als van het kwadraat ervan afgetrokken wordt het kwadraat van Bκ, wordt het kwadraat van BD verkregen, en daaruit ook BD zelf, en derhalve ook DE.
Nu is evenals bij de platbolle lens, waarvan het bolvormige oppervlak als buitenste genomen wordt, zo ook bij deze stand van de platholle lens, de aberratie ED vrijwel 7/6 maal de dikte CO (of GB).
Zodat gezegd moet worden dat deze holle lens op deze manier de evenwijdige stralen veel beter spreidt dan wanneer hij die eerst opvangt met het platte oppervlak.
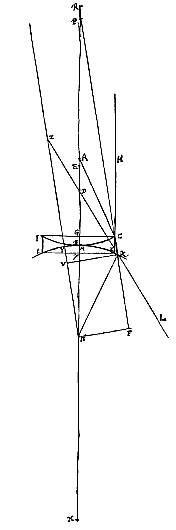 We beschouwen nu de dubbelholle lens IBCKBι. Van oppervlak IBC, dat de evenwijdige stralen opvangt, is het middelpunt A, en van het andere oppervlak ιBK is het middelpunt N. Door deze punten gaat de as NA van de lens, aan weerskanten verlengd verondersteld. Als dan gegeven zijn de halve diameters AB en NM, is ook BE te geven, de afstand van het spreidingspunt der evenwijdige stralen. Want met BR driemaal BA, en MX driemaal MN, staat vast dat RX : RN = RB : RE {* voorstel I.I}; waarmee duidelijk is dat RE, en daarom ook EB, bekend is.
We beschouwen nu de dubbelholle lens IBCKBι. Van oppervlak IBC, dat de evenwijdige stralen opvangt, is het middelpunt A, en van het andere oppervlak ιBK is het middelpunt N. Door deze punten gaat de as NA van de lens, aan weerskanten verlengd verondersteld. Als dan gegeven zijn de halve diameters AB en NM, is ook BE te geven, de afstand van het spreidingspunt der evenwijdige stralen. Want met BR driemaal BA, en MX driemaal MN, staat vast dat RX : RN = RB : RE {* voorstel I.I}; waarmee duidelijk is dat RE, en daarom ook EB, bekend is.
We stellen verder dat de uiterste straal HC, die evenwijdig is met de as, na de eerste breking aan oppervlak IBC zo langs Cκ loopt, dat deze, achterwaarts verlengd, met de as samenkomt in P. En dat hij door de andere breking, aan oppervlak ιMK, gebroken wordt volgens κL, die achterwaarts verlengd met de as samenkomt in D. De aberratie van de uiterste straal HC is dus DE, waarvan we zullen aantonen dat hij met een iets andere methode gevonden wordt dan bij de dubbelbolle lens [<].
Maar eerst moet opgemerkt worden dat, ook al wordt verondersteld dat oppervlak ιMK verlengd is naar κ, zodat het wat breder is dan oppervlak IBC, hier toch de dikte van de lens gesteld wordt op die Gγ die gelijk is aan CK, te weten het gedeelte van de rechte HC dat tussen de beide oppervlakken onderschept is. Zoals ook de opening van de lens geacht moet worden te zijn tweemaal CG, en niet tweemaal de afstand van punt κ tot de as.
Laat nu NZ evenwijdig zijn met CP, en laat het verlengde van κD hem in Z ontmoeten. We trekken vervolgens κV loodrecht op NZ, en NF op het verlengde van Pκ.
|
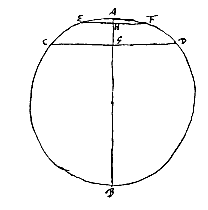 Gegeven van eenzelfde cirkel de kleine segmenten CAD en EAF, die beide de cirkeldiameter AB doormidden snijden, en van de segmenten zijn de hoogten AG en AH. Ik zeg dat de verhouding AG : AH bij benadering dezelfde is als die van de kwadraten van de basis CD tot de kwadraten van de basis EF.
Gegeven van eenzelfde cirkel de kleine segmenten CAD en EAF, die beide de cirkeldiameter AB doormidden snijden, en van de segmenten zijn de hoogten AG en AH. Ik zeg dat de verhouding AG : AH bij benadering dezelfde is als die van de kwadraten van de basis CD tot de kwadraten van de basis EF.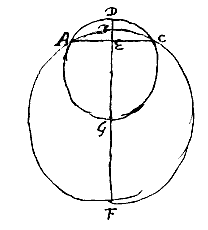 Gegeven de kleine segmenten ABC en ADC, van ongelijke cirkels, met dezelfde basis AC, en doormidden gedeeld door de rechte DE; op deze rechte liggen ook de middellijnen van de cirkels, te weten BF van die waarvan ABC een segment is, en DG van de kleinere cirkel waarvan ADC een segment is. Ik zeg dat zoals BF tot DG is, zo ook bij benadering de hoogte DE tot BE.
Gegeven de kleine segmenten ABC en ADC, van ongelijke cirkels, met dezelfde basis AC, en doormidden gedeeld door de rechte DE; op deze rechte liggen ook de middellijnen van de cirkels, te weten BF van die waarvan ABC een segment is, en DG van de kleinere cirkel waarvan ADC een segment is. Ik zeg dat zoals BF tot DG is, zo ook bij benadering de hoogte DE tot BE. 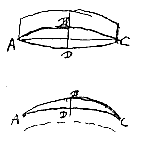 Dikte van een bolle lens
Dikte van een bolle lens 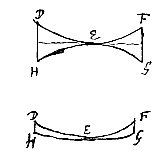
 Stel ten eerste dat van de lenzen de ene AB platbol is, waarbij oppervlak ACB de halve bollingsdiameter DC heeft. De lensdikte is CE, en de brandpuntsafstand CF, die het dubbele van CD zal zijn [
Stel ten eerste dat van de lenzen de ene AB platbol is, waarbij oppervlak ACB de halve bollingsdiameter DC heeft. De lensdikte is CE, en de brandpuntsafstand CF, die het dubbele van CD zal zijn [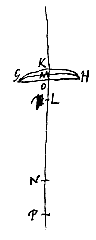
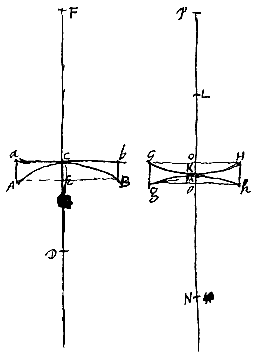 Laat er nu ook een platholle lens ACBba zijn, met beide oppervlakken aangrenzend in C; en van oppervlak ACB is het middelpunt weer D, en CF is de afstand van het spreidingspunt, die het dubbele is van CD [
Laat er nu ook een platholle lens ACBba zijn, met beide oppervlakken aangrenzend in C; en van oppervlak ACB is het middelpunt weer D, en CF is de afstand van het spreidingspunt, die het dubbele is van CD [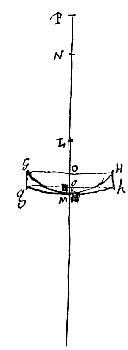 En de andere lens, òf dubbelhol òf bolhol, is GKHhMg, met een breedte gelijk aan die van AB, en een afstand van het spreidingspunt PM gelijk aan FC.
En de andere lens, òf dubbelhol òf bolhol, is GKHhMg, met een breedte gelijk aan die van AB, en een afstand van het spreidingspunt PM gelijk aan FC. 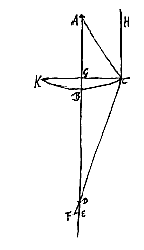
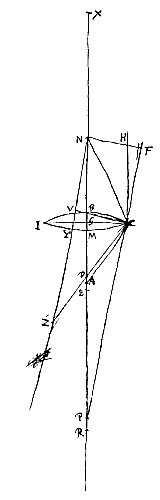 We beschouwen nu een lens IC die aan beide kanten bol is, en van het oppervlak IBC, dat de evenwijdige stralen opvangt, is het middelpunt A, terwijl van oppervlak IMC het middelpunt N is; en door beide gaat de as NA van de lens, die aan weerskanten verlengd wordt. Verder stellen we dat gegeven zijn de halve diameters AB en NM, en de halve lensdiameter GC. Als nu gesteld wordt dat E brandpunt is van lens IC, en als genomen wordt BR = 3 BA en MX = 3 MN, zal moeten gelden RX : RN = RM : RE [
We beschouwen nu een lens IC die aan beide kanten bol is, en van het oppervlak IBC, dat de evenwijdige stralen opvangt, is het middelpunt A, terwijl van oppervlak IMC het middelpunt N is; en door beide gaat de as NA van de lens, die aan weerskanten verlengd wordt. Verder stellen we dat gegeven zijn de halve diameters AB en NM, en de halve lensdiameter GC. Als nu gesteld wordt dat E brandpunt is van lens IC, en als genomen wordt BR = 3 BA en MX = 3 MN, zal moeten gelden RX : RN = RM : RE [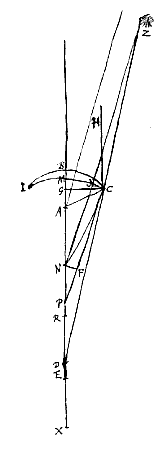 Bij de lens in de vorm van een maansikkel is de methode van berekening dezelfde als bij de dubbelbolle lens, of nu het bolle oppervlak de evenwijdige stralen opvangt, of het holle; van beide gevallen hebben we hier een figuur toegevoegd. Er moet echter op gelet worden dat niet de som, maar het verschil van de twee NZ en CP hier tot CP is als NP tot PD.
Bij de lens in de vorm van een maansikkel is de methode van berekening dezelfde als bij de dubbelbolle lens, of nu het bolle oppervlak de evenwijdige stralen opvangt, of het holle; van beide gevallen hebben we hier een figuur toegevoegd. Er moet echter op gelet worden dat niet de som, maar het verschil van de twee NZ en CP hier tot CP is als NP tot PD.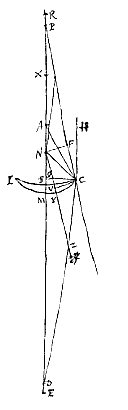 Daarmee kunnen ook de maansikkelvormige lenzen onderling, en met dubbelbolle lenzen, vergeleken worden. Zoals wanneer bijvoorbeeld in het vorige geval gesteld wordt dat de halve diameter van het holle oppervlak driemaal AB is, dus a = 1, n = 3, dan wordt ED = 3q, dus driemaal de dikte BM. Maar bij de beste lens (hierboven gedefinieerd [
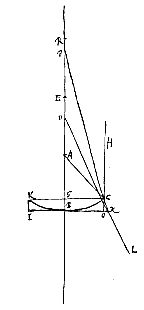
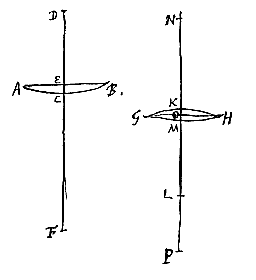
Daarmee kunnen ook de maansikkelvormige lenzen onderling, en met dubbelbolle lenzen, vergeleken worden. Zoals wanneer bijvoorbeeld in het vorige geval gesteld wordt dat de halve diameter van het holle oppervlak driemaal AB is, dus a = 1, n = 3, dan wordt ED = 3q, dus driemaal de dikte BM. Maar bij de beste lens (hierboven gedefinieerd [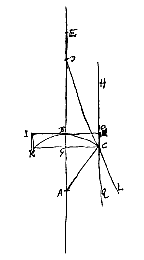 We beschouwen eerst de platholle lens KBCOI, waarbij het platte oppervlak OI de evenwijdige stralen opvangt; en het middelpunt van het holle oppervlak is A, de as van de lens ABE. Verder is de uiterste met de as evenwijdige straal HO, die natuurlijk ongebroken door het platte oppervlak gaat. Doch als hij uit het holle oppervlak treedt, wordt hij zo gebroken dat hij doorgaat langs CL, die achterwaarts verlengd samenkomt met de as in D. En het spreidingspunt van de lens is E, dat gevonden wordt door BE tweemaal zo groot als BA te nemen, zoals vast staat volgens voorstel I.
We beschouwen eerst de platholle lens KBCOI, waarbij het platte oppervlak OI de evenwijdige stralen opvangt; en het middelpunt van het holle oppervlak is A, de as van de lens ABE. Verder is de uiterste met de as evenwijdige straal HO, die natuurlijk ongebroken door het platte oppervlak gaat. Doch als hij uit het holle oppervlak treedt, wordt hij zo gebroken dat hij doorgaat langs CL, die achterwaarts verlengd samenkomt met de as in D. En het spreidingspunt van de lens is E, dat gevonden wordt door BE tweemaal zo groot als BA te nemen, zoals vast staat volgens voorstel I. Maar bij dezelfde lens, andersom geplaatst (zodat namelijk het holle oppervlak KBC de evenwijdige stralen opvangt), zijn er twee brekingen. Want straal HC wordt eerst gebroken in C, en loopt vandaar langs Cκ, die achterwaarts verlengd met de as samenkomt in P, en weer uit het platte oppervlak komend in κ gaat hij verder langs κL, die achterwaarts verlengd met de as samenkomt voor P, neem aan in D. Nu is de afstand BE van het spreidingspunt bij de lens in deze stand weer het dubbele van BA. En de aberratie ED van de uiterste straal wordt gevonden op de volgende manier.
Maar bij dezelfde lens, andersom geplaatst (zodat namelijk het holle oppervlak KBC de evenwijdige stralen opvangt), zijn er twee brekingen. Want straal HC wordt eerst gebroken in C, en loopt vandaar langs Cκ, die achterwaarts verlengd met de as samenkomt in P, en weer uit het platte oppervlak komend in κ gaat hij verder langs κL, die achterwaarts verlengd met de as samenkomt voor P, neem aan in D. Nu is de afstand BE van het spreidingspunt bij de lens in deze stand weer het dubbele van BA. En de aberratie ED van de uiterste straal wordt gevonden op de volgende manier. We beschouwen nu de dubbelholle lens IBCKBι. Van oppervlak IBC, dat de evenwijdige stralen opvangt, is het middelpunt A, en van het andere oppervlak ιBK is het middelpunt N. Door deze punten gaat de as NA van de lens, aan weerskanten verlengd verondersteld. Als dan gegeven zijn de halve diameters AB en NM, is ook BE te geven, de afstand van het spreidingspunt der evenwijdige stralen. Want met BR driemaal BA, en MX driemaal MN, staat vast dat RX : RN = RB : RE {* voorstel
We beschouwen nu de dubbelholle lens IBCKBι. Van oppervlak IBC, dat de evenwijdige stralen opvangt, is het middelpunt A, en van het andere oppervlak ιBK is het middelpunt N. Door deze punten gaat de as NA van de lens, aan weerskanten verlengd verondersteld. Als dan gegeven zijn de halve diameters AB en NM, is ook BE te geven, de afstand van het spreidingspunt der evenwijdige stralen. Want met BR driemaal BA, en MX driemaal MN, staat vast dat RX : RN = RB : RE {* voorstel 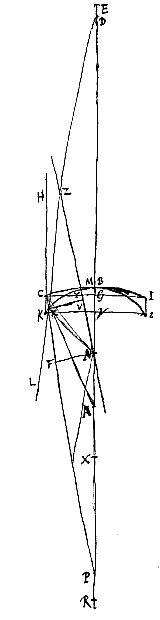 Met deze formule kunnen alle dubbelholle lenzen onderling vergeleken worden, en kan men vinden hoeveel beter de ene de stralen uitspreidt dan de andere. En de beste is te vinden uit de bepaling van het minimum, en deze is hier noodzakelijk dezelfde als bij de dubbelbolle lens [
Met deze formule kunnen alle dubbelholle lenzen onderling vergeleken worden, en kan men vinden hoeveel beter de ene de stralen uitspreidt dan de andere. En de beste is te vinden uit de bepaling van het minimum, en deze is hier noodzakelijk dezelfde als bij de dubbelbolle lens [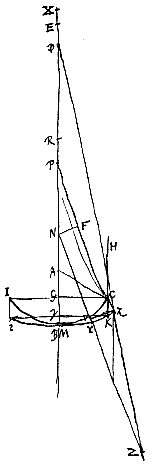 zal de Regel om de aberratie ED van de uiterste straal te vinden, in het eerste geval deze zijn:
zal de Regel om de aberratie ED van de uiterste straal te vinden, in het eerste geval deze zijn: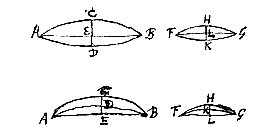 Dat de dikten van dergelijke lenzen zich tot elkaar verhouden als de kwadraten van de breedten, wordt gemakkelijk aangetoond uit wat bewezen is in voorstel
Dat de dikten van dergelijke lenzen zich tot elkaar verhouden als de kwadraten van de breedten, wordt gemakkelijk aangetoond uit wat bewezen is in voorstel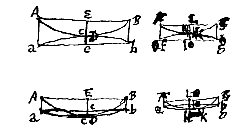 Bij dubbelholle lenzen, waarvan de oppervlakken ACB en aDb verondersteld worden elkaar te raken, en evenzo FKG en fKg; en waarvan de dikten zijn Ee en Ll, is het bewijs hetzelfde als bij de dubbelbolle lenzen. En bij bolholle hetzelfde als bij de maansikkellenzen. Als echter één van de oppervlakken van bolle of holle lenzen plat is, is het bewijs duidelijk uit wat hier gezegd is.
Bij dubbelholle lenzen, waarvan de oppervlakken ACB en aDb verondersteld worden elkaar te raken, en evenzo FKG en fKg; en waarvan de dikten zijn Ee en Ll, is het bewijs hetzelfde als bij de dubbelbolle lenzen. En bij bolholle hetzelfde als bij de maansikkellenzen. Als echter één van de oppervlakken van bolle of holle lenzen plat is, is het bewijs duidelijk uit wat hier gezegd is.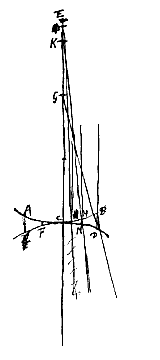 Bij holle lenzen is het bewijs van deze zaak gemakkelijker, en het hangt af van het naast voorgaande. Want laat gegeven zijn de holle lens ACBDCF, waarvan de as CE is, en het spreidingspunt E. En een met de as evenwijdige straal die in het punt B invalt, wordt zo afgebogen dat hij achterwaarts verlengd samenkomt met de as in G. En een andere straal die evenwijdig is met de as, maar er dichterbij invalt in het punt H, wordt zo afgebogen dat hij achterwaarts verlengd samenkomt met de as in K.
Bij holle lenzen is het bewijs van deze zaak gemakkelijker, en het hangt af van het naast voorgaande. Want laat gegeven zijn de holle lens ACBDCF, waarvan de as CE is, en het spreidingspunt E. En een met de as evenwijdige straal die in het punt B invalt, wordt zo afgebogen dat hij achterwaarts verlengd samenkomt met de as in G. En een andere straal die evenwijdig is met de as, maar er dichterbij invalt in het punt H, wordt zo afgebogen dat hij achterwaarts verlengd samenkomt met de as in K. 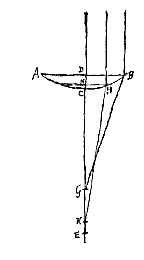 Niet ongelijk hieraan is ook het bewijs bij de platbolle lens, wanneer het platte oppervlak in de evenwijdige stralen wordt gehouden. Want we beschouwen een dergelijke lens ACB, met de as DE, en brandpunt E, waarin evenwijdige stralen gebroken worden die invallen in de punten B en H van het bolle oppervlak, nadat ze ongebroken door het platte oppervlak AB zijn gegaan; ze ontmoeten de as in G en K. Als hier dus de loodlijn HN op de as DC getrokken is, zijn weer om zo te zeggen twee platbolle lenzen te beschouwen, waarvan de dikten DC en NC zijn. Zoals nu het kwadraat van BD tot het kwadraat van HN, zo is DC tot NC; en zoals DC tot NC, zo is de aberratie EG tot EK, wanneer EG gelijk gesteld wordt aan 9/2 DC [
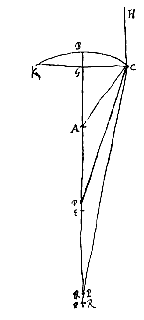
Niet ongelijk hieraan is ook het bewijs bij de platbolle lens, wanneer het platte oppervlak in de evenwijdige stralen wordt gehouden. Want we beschouwen een dergelijke lens ACB, met de as DE, en brandpunt E, waarin evenwijdige stralen gebroken worden die invallen in de punten B en H van het bolle oppervlak, nadat ze ongebroken door het platte oppervlak AB zijn gegaan; ze ontmoeten de as in G en K. Als hier dus de loodlijn HN op de as DC getrokken is, zijn weer om zo te zeggen twee platbolle lenzen te beschouwen, waarvan de dikten DC en NC zijn. Zoals nu het kwadraat van BD tot het kwadraat van HN, zo is DC tot NC; en zoals DC tot NC, zo is de aberratie EG tot EK, wanneer EG gelijk gesteld wordt aan 9/2 DC [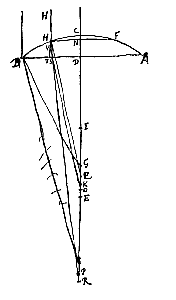 We stellen dat de uiterste met de as evenwijdige straal, die in B invalt, samenkomt met de as in G, zodat de aberratie ervan EG is. En dat een evenwijdige straal die invalt in punt H, vandaar langs de rechte HP loopt, die het oppervlak AB snijdt in S, en nadat daar de tweede breking heeft plaats gevonden komt hij met de as samen in K, zodat de aberratie van deze straal EK is.
We stellen dat de uiterste met de as evenwijdige straal, die in B invalt, samenkomt met de as in G, zodat de aberratie ervan EG is. En dat een evenwijdige straal die invalt in punt H, vandaar langs de rechte HP loopt, die het oppervlak AB snijdt in S, en nadat daar de tweede breking heeft plaats gevonden komt hij met de as samen in K, zodat de aberratie van deze straal EK is.