|
Aldus in een telescoop die 30 voet lang is, en die de planeten honderdnegenmaal vergroot in diameter, en daardoor een openingsbreedte zou vereisen die zich zou verhouden tot die van de pupil als 109 tot 1; dat is, die van bijna 11 duim zou zijn (gesteld namelijk dat de pupilbreedte 1/10 duim is): bevonden wordt dat een opening met een breedte van 3 duim voldoende is. En die verzamelt minder dan een dertiende deel van het licht dat zou intreden bij een opening van 11 duim.
Maar de pupilbreedte heeft niet een vastgestelde waarde, en is niet altijd dezelfde, en ook kan niet nauwkeurig bepaald worden welke helderheid voldoende is. En aan planeten die verder verwijderd en daardoor minder goed zichtbaar zijn moet men een wat grotere helderheid geven, dan aan planeten dichter bij de Zon. Over de reden hiervan zal in het volgende gesproken worden.
Dit echter moet in het algemeen gezocht worden: hoe bij een gegeven telescoop die goed ingericht is (naar de ervaring heeft uitgewezen), en waarbij de brandpuntsafstanden van de twee lenzen gegeven zijn, en met de opening van de buitenste lens zo groot als toelaatbaar is, hoe, zeg ik, hieruit andere mogelijke telescopen af te leiden zijn van welke lengte dan ook [<], zodanig dat ze objecten even helder laten zien, en even scherp. Want hierdoor komt men te weten wat, en hoeveel, het kan helpen als men de telescooplengte vergroot. Eveneens of de glasschijven juist bewerkt en goed gepolijst zijn, of niet.
En om van de scherpte de reden te geven, het is te weten dat deze door twee oorzaken bedorven wordt, waarvan de ene is, dat een bolvormige bolling van de lenzen niet de stralen die uit een punt van het object weggaan naar één punt samenbrengt, maar wat doet afwijken (zoals in het voorgaande aangetoond is [<]).
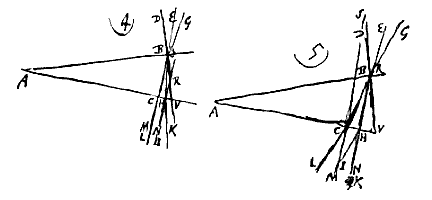
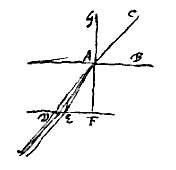 De andere reden is dat een straal die op het oppervlak van een dichter doorzichtig lichaam schuin invalt, en die voor een rechte lijn te houden is, nadat hij gebroken is niet langer langs een lijn loopt, maar zich als het ware uitstrooit in meer stralen, door heel kleine hoeken gescheiden, en met kleuren doortrokken. Zoals wanneer de straal CA op het glasoppervlak AB invalt: als deze gebroken is zal hij zich uitstrooien over de kleine hoek DAE, waarvan de zijde AD, die meer weggaat van de loodlijn GAF, een rode kleur zal dragen, en de andere uiterste AE een donkerviolette kleur; en tussen D en E zullen verschijnen geel, groen en blauw, in dezelfde volgorde als waarin ze gewoonlijk te zien zijn in de regenboog.
De andere reden is dat een straal die op het oppervlak van een dichter doorzichtig lichaam schuin invalt, en die voor een rechte lijn te houden is, nadat hij gebroken is niet langer langs een lijn loopt, maar zich als het ware uitstrooit in meer stralen, door heel kleine hoeken gescheiden, en met kleuren doortrokken. Zoals wanneer de straal CA op het glasoppervlak AB invalt: als deze gebroken is zal hij zich uitstrooien over de kleine hoek DAE, waarvan de zijde AD, die meer weggaat van de loodlijn GAF, een rode kleur zal dragen, en de andere uiterste AE een donkerviolette kleur; en tussen D en E zullen verschijnen geel, groen en blauw, in dezelfde volgorde als waarin ze gewoonlijk te zien zijn in de regenboog.
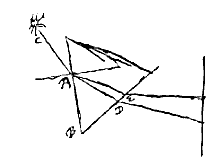
Dat dit zo is, en wat daaruit volgt, heeft de zeer geleerde heer Isaac Newton enige tijd geleden opgemerkt; en door met een glazen prisma gebroken zonnestralen op te vangen op een donkere plaats heeft hij waargenomen dat deze straalverstrooiing volgens deze regel gebeurt: alsof de brekingen van de verschillend gekleurde stralen verschillend zouden zijn, sommige groter dan andere, en alsof de straal CA ze allemaal zou bevatten. En dat de buitenste in AD en AE zo gebroken worden dat de sinus van hoek GAC wel tot de sinus van hoek FAD zou zijn als 68 tot 44, maar tot de sinus van hoek FAE als 69 tot 44.
|
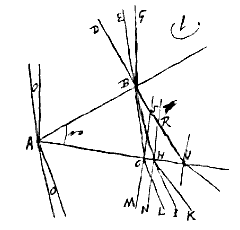 Veronderstel dat de hoek BAC tussen de twee vlakken, die de massief glazen hoek begrenzen, kleiner is dan 19°. En verder dat er in het vlak door ABC ook de rechte lijn DBV is, die het vlak AB loodrecht snijdt in B, en dat de stralen EB en GB daarmee een hoek maken, kleiner dan 29°, aan de van A afgekeerde kant. Hiervan loopt de binnenste EB in het doorzichtige lichaam langs BH, en hij komt er uit als HK. Maar GB loopt in het doorzichtige lichaam langs BC, en komt er uit als CL.
Veronderstel dat de hoek BAC tussen de twee vlakken, die de massief glazen hoek begrenzen, kleiner is dan 19°. En verder dat er in het vlak door ABC ook de rechte lijn DBV is, die het vlak AB loodrecht snijdt in B, en dat de stralen EB en GB daarmee een hoek maken, kleiner dan 29°, aan de van A afgekeerde kant. Hiervan loopt de binnenste EB in het doorzichtige lichaam langs BH, en hij komt er uit als HK. Maar GB loopt in het doorzichtige lichaam langs BC, en komt er uit als CL.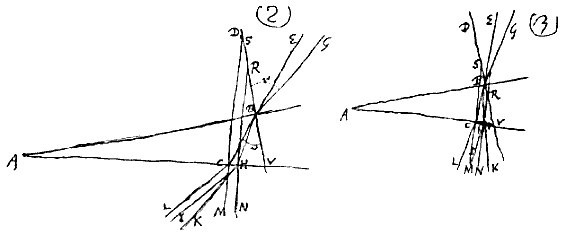
 De andere reden is dat een straal die op het oppervlak van een dichter doorzichtig lichaam schuin invalt, en die voor een rechte lijn te houden is, nadat hij gebroken is niet langer langs een lijn loopt, maar zich als het ware uitstrooit in meer stralen, door heel kleine hoeken gescheiden, en met kleuren doortrokken. Zoals wanneer de straal CA op het glasoppervlak AB invalt: als deze gebroken is zal hij zich uitstrooien over de kleine hoek DAE, waarvan de zijde AD, die meer weggaat van de loodlijn GAF, een rode kleur zal dragen, en de andere uiterste AE een donkerviolette kleur; en tussen D en E zullen verschijnen geel, groen en blauw, in dezelfde volgorde als waarin ze gewoonlijk te zien zijn in de regenboog.
De andere reden is dat een straal die op het oppervlak van een dichter doorzichtig lichaam schuin invalt, en die voor een rechte lijn te houden is, nadat hij gebroken is niet langer langs een lijn loopt, maar zich als het ware uitstrooit in meer stralen, door heel kleine hoeken gescheiden, en met kleuren doortrokken. Zoals wanneer de straal CA op het glasoppervlak AB invalt: als deze gebroken is zal hij zich uitstrooien over de kleine hoek DAE, waarvan de zijde AD, die meer weggaat van de loodlijn GAF, een rode kleur zal dragen, en de andere uiterste AE een donkerviolette kleur; en tussen D en E zullen verschijnen geel, groen en blauw, in dezelfde volgorde als waarin ze gewoonlijk te zien zijn in de regenboog.

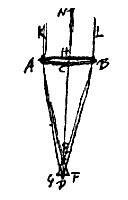 En hieruit heeft hij verder opgemaakt dat in een willekeurige glazen lens, zoals AB, met as CD, geldt: als van de buitenste met de as evenwijdige stralen KA en LB, het deel dat het minst gebroken wordt, en dat de rode kleur draagt, met de as samenkomt in D, en het maximaal gebroken en violette deel in E, dat dan ED gelijk is aan 1/50 CD. En daarom, als AE en BE doorgetrokken worden totdat ze in F en G de rechte ontmoeten die door D getrokken is evenwijdig met de lens AB, dat dan GF, de diameter van het afwijkingscirkeltje, gelijk wordt aan het vijftigste deel van de diameter AB*). Dientengevolge zal ook hoek DAF geacht worden 1/50 van hoek ADC uit te maken.
En hieruit heeft hij verder opgemaakt dat in een willekeurige glazen lens, zoals AB, met as CD, geldt: als van de buitenste met de as evenwijdige stralen KA en LB, het deel dat het minst gebroken wordt, en dat de rode kleur draagt, met de as samenkomt in D, en het maximaal gebroken en violette deel in E, dat dan ED gelijk is aan 1/50 CD. En daarom, als AE en BE doorgetrokken worden totdat ze in F en G de rechte ontmoeten die door D getrokken is evenwijdig met de lens AB, dat dan GF, de diameter van het afwijkingscirkeltje, gelijk wordt aan het vijftigste deel van de diameter AB*). Dientengevolge zal ook hoek DAF geacht worden 1/50 van hoek ADC uit te maken.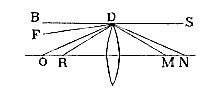 Opgemerkt*) kan worden dat voorstel VI [
Opgemerkt*) kan worden dat voorstel VI [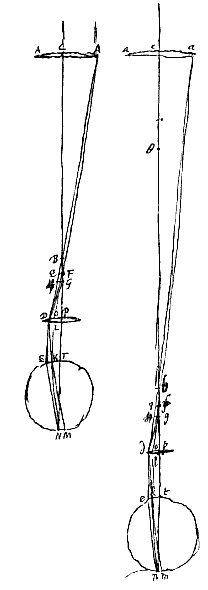 Beschouw een telescoop die samengesteld is uit de lenzen AC en DP, AC als buitenste, DP als oculair. De as van de telescoop die door het midden van elk van beide lenzen gaat is CP, die de pupil van het oog snijdt in het punt T, en de achterkant treft in N. De brandpuntsafstand van lens AC is CF, van lens DP is de brandpuntsafstand PF. De halve openingsbreedte is AC.
Beschouw een telescoop die samengesteld is uit de lenzen AC en DP, AC als buitenste, DP als oculair. De as van de telescoop die door het midden van elk van beide lenzen gaat is CP, die de pupil van het oog snijdt in het punt T, en de achterkant treft in N. De brandpuntsafstand van lens AC is CF, van lens DP is de brandpuntsafstand PF. De halve openingsbreedte is AC.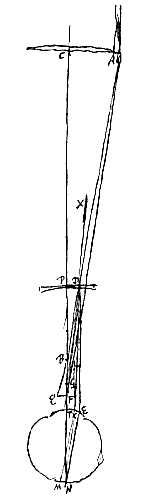 Bij telescopen die zijn samengesteld uit een bolle en een holle lens kan hetzelfde aangetoond worden, met een volkomen gelijkvormig bewijs, behalve dat dan de afstand van het spreidingspunt zal zijn wat hier de brandpuntsafstand van de bolle oculairlens was. Maar van deze holle lenzen maakt men bij de samenstelling nu bijna geen gebruik, wegens de beperktheid van de ruimte, die ze overlaten voor het blikveld in de telescopen [
Bij telescopen die zijn samengesteld uit een bolle en een holle lens kan hetzelfde aangetoond worden, met een volkomen gelijkvormig bewijs, behalve dat dan de afstand van het spreidingspunt zal zijn wat hier de brandpuntsafstand van de bolle oculairlens was. Maar van deze holle lenzen maakt men bij de samenstelling nu bijna geen gebruik, wegens de beperktheid van de ruimte, die ze overlaten voor het blikveld in de telescopen [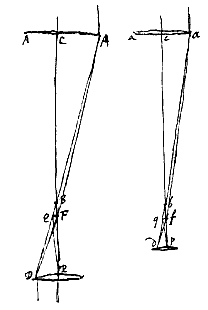 Laat van de lenzen AA en aa de brandpuntsafstanden CF en cf voor de evenwijdige rode stralen gelijk zijn, en evenzo gelijk CB en cb, de brandpuntsafstanden voor de violette stralen; de openingen echter ongelijk, waarvan de diameters zijn AA en aa. En laat dezelfde verhouding als deze gelden voor de brandpuntsafstanden FP en fp van de oculairlenzen. Als voorts getrokken zijn bij beide (zoals boven [
Laat van de lenzen AA en aa de brandpuntsafstanden CF en cf voor de evenwijdige rode stralen gelijk zijn, en evenzo gelijk CB en cb, de brandpuntsafstanden voor de violette stralen; de openingen echter ongelijk, waarvan de diameters zijn AA en aa. En laat dezelfde verhouding als deze gelden voor de brandpuntsafstanden FP en fp van de oculairlenzen. Als voorts getrokken zijn bij beide (zoals boven [