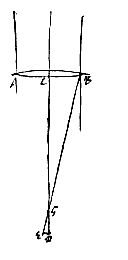
 Stel dan dat van een dergelijke bolle lens de opening AB is, de as CD, en D het brandpunt, of het punt waarnaar stralen verzameld worden die evenwijdig zijn aan de as. Verder is de aberratie van de uiterste straal DG, en wordt de gebrokene BG van deze straal doorgetrokken totdat hij in E een paneel ontmoet, dat we ons voorstellen door het brandpunt D, evenwijdig met de lens AB. Daar dus van de overige met de as evenwijdige stralen de gebrokenen des te dichter bij het brandpunt D samenkomen, naarmate ze dichter bij de as lopen, volgt dat de uitersten van de hele serie evenwijdige stralen (of: die uit één punt van het object voortkomen) op het paneel een cirkeltje beslaan, met halve diameter DE; en van hoe kleiner grootte dit cirkeltje is, des te perfecter zal de voorstelling van het object zijn op het paneel.
Stel dan dat van een dergelijke bolle lens de opening AB is, de as CD, en D het brandpunt, of het punt waarnaar stralen verzameld worden die evenwijdig zijn aan de as. Verder is de aberratie van de uiterste straal DG, en wordt de gebrokene BG van deze straal doorgetrokken totdat hij in E een paneel ontmoet, dat we ons voorstellen door het brandpunt D, evenwijdig met de lens AB. Daar dus van de overige met de as evenwijdige stralen de gebrokenen des te dichter bij het brandpunt D samenkomen, naarmate ze dichter bij de as lopen, volgt dat de uitersten van de hele serie evenwijdige stralen (of: die uit één punt van het object voortkomen) op het paneel een cirkeltje beslaan, met halve diameter DE; en van hoe kleiner grootte dit cirkeltje is, des te perfecter zal de voorstelling van het object zijn op het paneel.
Zoals verder de afbeeldingen met twee verschillende lenzen even welgevormd en scherp zullen zijn wanneer ze deze aberratiecirkels gelijk maken, zo ook zal het zicht even scherp worden met verschillende telescopen, wanneer hierdoor ook afbeeldingen achterin het oog geprojecteerd worden die even scherp begrensd zijn, d.w.z. waarin de aberratiecirkels van gelijke breedte zijn. En ik denk dat hier als grondslag niets zekerders of duidelijkers vastgesteld kan worden.
Om nu met minder moeite de breedte te onderzoeken van die cirkeltjes achterin het oog, zullen we, aangezien het schijnt dat de oculairlens enige moeilijkheid kan geven, eerst aantonen,
De aberratiecirkeltjes achterin het oog van iemand die door een telescoop kijkt, zijn bijna alleen afkomstig van de aberratie van de buitenste lens, terwijl de oculairlens nauwelijks iets aan hun breedte toedoet; zodat deze lens in de telescoop als perfect beschouwd kan worden, d.w.z. alsof hij stralen die vanaf een punt komen exact evenwijdig zou maken.
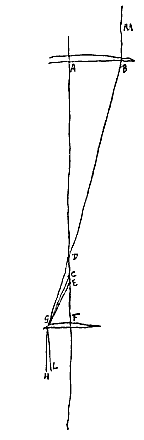
Beschouw namelijk de buitenste lens AB van een telescoop, en het oculair GF, van welke twee lenzen C een brandpunt is. En de uiterste met de as evenwijdige straal MB snijdt de as in D, de aberratie DC makend, en ontmoet de lens GF in G; en trek CG.
Als we ons nu voorstellen dat de straal HG evenwijdig met de as invalt op lens FG, zal deze niet met de as samenkomen in C, brandpunt van lens GF, maar vòòr punt C in E, zó dat aberratie CE tot aberratie CD is als CF tot AC. Want daar AB en FG gelijkvormige stukken zijn van lenzen van dezelfde soort, staat vast dat beider aberraties van evenwijdige stralen die in B en G invallen zich tot elkaar verhouden als de brandpuntsafstanden van de lenzen.
En daarom zal dus ook andersom een straal die vanuit E invalt langs EG, afgebogen worden langs GH, evenwijdig aan de as. Maar de straal DG zal zo gebroken worden in GL, dat de hoek HGL gelijk wordt aan DGE {* [>]}. Dus zullen beide lenzen samen nu een straal, die evenwijdig met de as zou moeten zijn, doen afwijken met deze hoek HGL, gelijk aan DGE; terwijl deze straal slechts zou afwijken met een hoek gelijk aan DGC, als lens FG zodanig was dat hij stralen komend uit het brandpunt C evenwijdig met de as zou maken. Dan zou namelijk, als straal CG gebroken werd in GH, en straal DG als voren in GL, de hoek LGH gelijk zijn aan de hoek DGC.
|
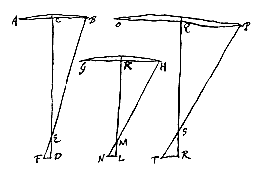 We beschouwen dus twee dergelijke lenzen, waarbij van de ene de opening AB is, de brandpuntsafstand CD; van de uiterste met de as evenwijdige straal is de gebrokene BEF, die de aberratie ED maakt, en de halve diameter van het aberratiecirkeltje is DF. Maar van de andere is de opening GH, de brandpuntsafstand KL; de gebrokene van de uiterste straal is HMN, die de aberratie ML maakt, en de halve diameter van het aberratiecirkeltje is LN.
We beschouwen dus twee dergelijke lenzen, waarbij van de ene de opening AB is, de brandpuntsafstand CD; van de uiterste met de as evenwijdige straal is de gebrokene BEF, die de aberratie ED maakt, en de halve diameter van het aberratiecirkeltje is DF. Maar van de andere is de opening GH, de brandpuntsafstand KL; de gebrokene van de uiterste straal is HMN, die de aberratie ML maakt, en de halve diameter van het aberratiecirkeltje is LN. 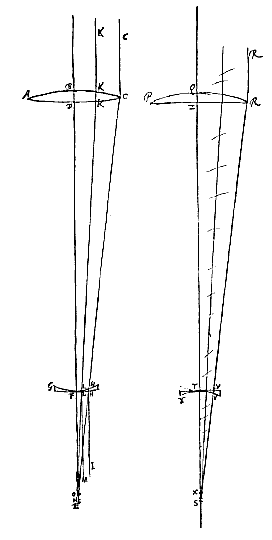 Gegeven de grote of buitenste lens ABCD van een telescoop, met de brandpuntsafstand DE. En bovendien is gegeven de vermenigvuldigingsfactor, d.w.z. waarmee we verlangen dat door een te maken telescoop de dingen vergroot worden, volgens de diameter; we noemen deze b : c, bij voorbeeld 10 : 1.
Gegeven de grote of buitenste lens ABCD van een telescoop, met de brandpuntsafstand DE. En bovendien is gegeven de vermenigvuldigingsfactor, d.w.z. waarmee we verlangen dat door een te maken telescoop de dingen vergroot worden, volgens de diameter; we noemen deze b : c, bij voorbeeld 10 : 1. 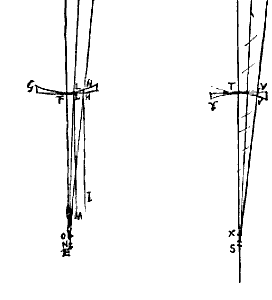 En hetzelfde is nu ook gemakkelijk aan te tonen voor een willekeurige straal die dichter bij de as is, zoals KK. Want laat deze, na de breking in lens AC, doorgaan langs de rechte KN, die de lens GH snijdt in L, en die samenkomt met de as in N, en trek LM evenwijdig met de as.
En hetzelfde is nu ook gemakkelijk aan te tonen voor een willekeurige straal die dichter bij de as is, zoals KK. Want laat deze, na de breking in lens AC, doorgaan langs de rechte KN, die de lens GH snijdt in L, en die samenkomt met de as in N, en trek LM evenwijdig met de as. 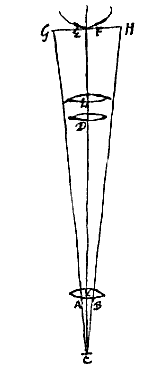
 Stel dan dat van een dergelijke bolle lens de opening AB is, de as CD, en D het brandpunt, of het punt waarnaar stralen verzameld worden die evenwijdig zijn aan de as. Verder is de aberratie van de uiterste straal DG, en wordt de gebrokene BG van deze straal doorgetrokken totdat hij in E een paneel ontmoet, dat we ons voorstellen door het brandpunt D, evenwijdig met de lens AB. Daar dus van de overige met de as evenwijdige stralen de gebrokenen des te dichter bij het brandpunt D samenkomen, naarmate ze dichter bij de as lopen, volgt dat de uitersten van de hele serie evenwijdige stralen (of: die uit één punt van het object voortkomen) op het paneel een cirkeltje beslaan, met halve diameter DE; en van hoe kleiner grootte dit cirkeltje is, des te perfecter zal de voorstelling van het object zijn op het paneel.
Stel dan dat van een dergelijke bolle lens de opening AB is, de as CD, en D het brandpunt, of het punt waarnaar stralen verzameld worden die evenwijdig zijn aan de as. Verder is de aberratie van de uiterste straal DG, en wordt de gebrokene BG van deze straal doorgetrokken totdat hij in E een paneel ontmoet, dat we ons voorstellen door het brandpunt D, evenwijdig met de lens AB. Daar dus van de overige met de as evenwijdige stralen de gebrokenen des te dichter bij het brandpunt D samenkomen, naarmate ze dichter bij de as lopen, volgt dat de uitersten van de hele serie evenwijdige stralen (of: die uit één punt van het object voortkomen) op het paneel een cirkeltje beslaan, met halve diameter DE; en van hoe kleiner grootte dit cirkeltje is, des te perfecter zal de voorstelling van het object zijn op het paneel. 
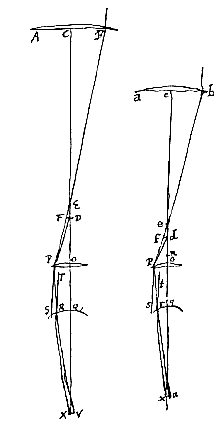 Stel namelijk dat er twee telescopen zijn van verschillende lengte, die de buitenste lenzen van dezelfde soort hebben, en van de ene is de buitenste lens (voorzover geopend) AB, de oculairlens OP, en beider brandpunten vallen samen in het punt D; het is namelijk nodig ze zo bijeen te plaatsen, opdat stralen die van een ver verwijderd punt naar de telescoop lopen evenwijdig bij het oog aankomen. En de pupil is QR, de achterkant van het oog is bij X, en alle middelpunten C, O, Q en X zijn op dezelfde rechte, die de as van de telescoop is.
Stel namelijk dat er twee telescopen zijn van verschillende lengte, die de buitenste lenzen van dezelfde soort hebben, en van de ene is de buitenste lens (voorzover geopend) AB, de oculairlens OP, en beider brandpunten vallen samen in het punt D; het is namelijk nodig ze zo bijeen te plaatsen, opdat stralen die van een ver verwijderd punt naar de telescoop lopen evenwijdig bij het oog aankomen. En de pupil is QR, de achterkant van het oog is bij X, en alle middelpunten C, O, Q en X zijn op dezelfde rechte, die de as van de telescoop is.