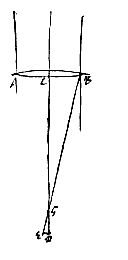
 Sit igitur convexae ejusmodi lentis apertura AB, axis CD, focus, seu punctum quo colliguntur radij ad axem paralleli, D. Aberratio autem radij extremi sit DG. et producatur BG refractio ejusdem radij quousque occurrat tabulae, quae per focum D lenti AB parallela intelligenda est, in E. Cum itaque radiorum caeterorum axi parallelorum refractiones, quanto quisque axi propinquior fertur, tanto propius concurrant ad focum D, sequitur extremitates totius seriei parallelorum, sive ab uno aliquo rei visae puncto manantium occupare in tabula circellum cujus semidiam. DE; qui circellus quo minori fuerit magnitudine tanto perfectior erit in tabula rei visae repraesentatio.
Sit igitur convexae ejusmodi lentis apertura AB, axis CD, focus, seu punctum quo colliguntur radij ad axem paralleli, D. Aberratio autem radij extremi sit DG. et producatur BG refractio ejusdem radij quousque occurrat tabulae, quae per focum D lenti AB parallela intelligenda est, in E. Cum itaque radiorum caeterorum axi parallelorum refractiones, quanto quisque axi propinquior fertur, tanto propius concurrant ad focum D, sequitur extremitates totius seriei parallelorum, sive ab uno aliquo rei visae puncto manantium occupare in tabula circellum cujus semidiam. DE; qui circellus quo minori fuerit magnitudine tanto perfectior erit in tabula rei visae repraesentatio.
Sicut autem aeque nitidae ac distinctae a duabus diversis lentibus picturae futurae sunt quando istos aberrationum circulos aequales facient; ita quoque aeque distincta visio diversis continget telescopijs, cum et ab illis in fundo oculi picturae aeque terminatae, hoc est in quibus aberrationum circuli aequali latitudine sint, describentur. Neque enim certius aut evidentius quicquam fundamenti vice hic statui posse existimo.
Ut autem minori negotio circellorum istorum in fundo oculi latitudo inquiratur, quoniam lens ocularis difficultatem aliquam adferre videri possit, ostendemus primo,
Circellos aberrationis, in fundo oculi per telescopium spectantis, fere tantum ab aberratione lentis exterioris oriri, lente oculari vix quicquam eorum latitudinem augente, adeo ut lens haec in telescopio tanquam perfecta censeri possit, hoc est, ac si radios a puncto venientes exacte parallelos redderet.
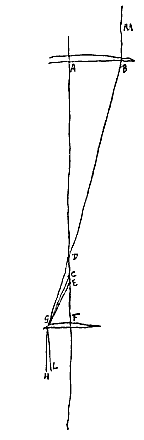
Sit enim lens telescopij exterior AB, ocularis GF, quarum utriusque foci sunt in puncto C. Radius autem extremus axi parallelus MB secet axem in D, faciens aberrationem DC, atque occurrat lenti GF in G; et jungatur CG.
Si jam fingamus radium HG axi parallelum incidere in lentem FG, is non conveniet cum axe in C, foco lentis GF, sed citra punctum C in E, ita ut aberratio CE sit ad aberrationem CD sicut AC ad CF [CF ad AC]. Nam cum AB et FG sint portiones similes lentium ejusdem generis, constat utriusque aberrationes radiorum parallelorum in B et G incidentium esse inter se sicut ipsae lentium foci distantiae.
Quamobrem itaque et vice versa radius, ex E incidens secundum EG, flectetur secundum GH axi parallelam. At radius DG ita refringetur in GL, ut angulus HGL fiat aequalis DGE {* [>]}. Itaque lens utraque simul nunc aberrare faciet radium qui axe parallelus esse debuerat hoc angulo HGL ipsi DGE aequali, qui radius tantum aberraret angulo aequali ipsi DGC si lens FG ejusmodi esset ut radios ex foco C egredientes axi parallelos redderet. Tunc enim radio CG refracto in GH, et radio DG, ut ante, in GL, aequaretur angulus LGH angulo DGC.
|
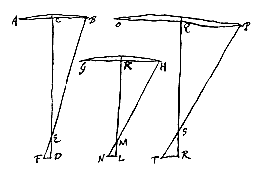 Sunto igitur duae ejusmodi lentes, quarum alterius apertura AB, foci distantia CD, radij extremi ad axem paralleli refractio BEF, faciens aberrationem ED, semidiametrum vero circelli aberrationis DF. Alterius vero apertura GH, foci distantia KL, radij extremi refractio HMN, faciens aberrationem ML, semidiametrum vero circelli aberrationis LN. Primo itaque ostendendum est aberrationem ED ad ML rationem habere compositam ex ratione quadrati AB ad qu. GH, sive qu. CB ad qu. KH, et ex ratione KL ad CD.
Sunto igitur duae ejusmodi lentes, quarum alterius apertura AB, foci distantia CD, radij extremi ad axem paralleli refractio BEF, faciens aberrationem ED, semidiametrum vero circelli aberrationis DF. Alterius vero apertura GH, foci distantia KL, radij extremi refractio HMN, faciens aberrationem ML, semidiametrum vero circelli aberrationis LN. Primo itaque ostendendum est aberrationem ED ad ML rationem habere compositam ex ratione quadrati AB ad qu. GH, sive qu. CB ad qu. KH, et ex ratione KL ad CD.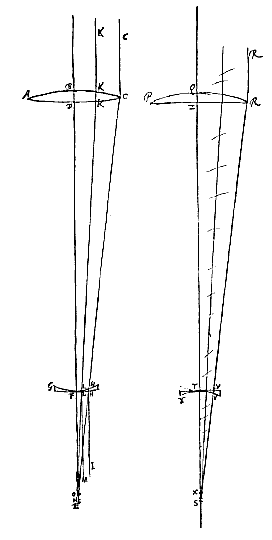 Data sit lens telescopij magna sive exterior ABCD, foci distantiam habens DE. ac data praeterea ratio multiplicationis, hoc est, secundum quam res visas telescopio construendo augeri cupimus secundum diametrum; quae sit ea quae b ad c, exempli gratia 10 ad 1. Divisa igitur DE in F, ut sit sicut b ad c, vel hic, 10 ad 1, ita DE ad EF; constat lentem cavam ad F constituendam fore, ut fiat dicta multiplicatio {* Prop. I.II.
Data sit lens telescopij magna sive exterior ABCD, foci distantiam habens DE. ac data praeterea ratio multiplicationis, hoc est, secundum quam res visas telescopio construendo augeri cupimus secundum diametrum; quae sit ea quae b ad c, exempli gratia 10 ad 1. Divisa igitur DE in F, ut sit sicut b ad c, vel hic, 10 ad 1, ita DE ad EF; constat lentem cavam ad F constituendam fore, ut fiat dicta multiplicatio {* Prop. I.II.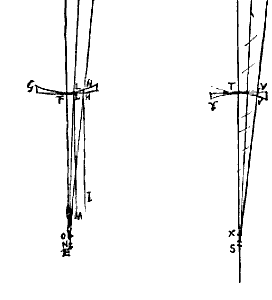 Idem vero et de radio quolibet axi propiore ut KK facile nunc ostendetur. Pergat enim hic, post refractionem in lente AC, secundum rectam KN quae secet lentem GH in L, et conveniat cum axe in N, et sit LM axi parallela. Cum ergo distantia puncti H ab axe sit ad distantiam L ut distantia C ad distantiam K erunt et quadrata earum distantiarum in eadem ratione. Sicut autem quadr. distantiae C ad quadr. distantiae K ita est aberratio radij CC quae est OE ad aberrationem radij KK, quae est NE {* Prop.
Idem vero et de radio quolibet axi propiore ut KK facile nunc ostendetur. Pergat enim hic, post refractionem in lente AC, secundum rectam KN quae secet lentem GH in L, et conveniat cum axe in N, et sit LM axi parallela. Cum ergo distantia puncti H ab axe sit ad distantiam L ut distantia C ad distantiam K erunt et quadrata earum distantiarum in eadem ratione. Sicut autem quadr. distantiae C ad quadr. distantiae K ita est aberratio radij CC quae est OE ad aberrationem radij KK, quae est NE {* Prop. 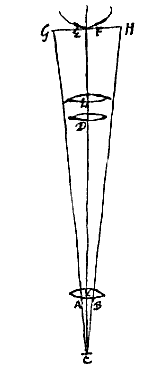
 Sit igitur convexae ejusmodi lentis apertura AB, axis CD, focus, seu punctum quo colliguntur radij ad axem paralleli, D. Aberratio autem radij extremi sit DG. et producatur BG refractio ejusdem radij quousque occurrat tabulae, quae per focum D lenti AB parallela intelligenda est, in E. Cum itaque radiorum caeterorum axi parallelorum refractiones, quanto quisque axi propinquior fertur, tanto propius concurrant ad focum D, sequitur extremitates totius seriei parallelorum, sive ab uno aliquo rei visae puncto manantium occupare in tabula circellum cujus semidiam. DE; qui circellus quo minori fuerit magnitudine tanto perfectior erit in tabula rei visae repraesentatio.
Sit igitur convexae ejusmodi lentis apertura AB, axis CD, focus, seu punctum quo colliguntur radij ad axem paralleli, D. Aberratio autem radij extremi sit DG. et producatur BG refractio ejusdem radij quousque occurrat tabulae, quae per focum D lenti AB parallela intelligenda est, in E. Cum itaque radiorum caeterorum axi parallelorum refractiones, quanto quisque axi propinquior fertur, tanto propius concurrant ad focum D, sequitur extremitates totius seriei parallelorum, sive ab uno aliquo rei visae puncto manantium occupare in tabula circellum cujus semidiam. DE; qui circellus quo minori fuerit magnitudine tanto perfectior erit in tabula rei visae repraesentatio. 
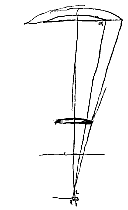
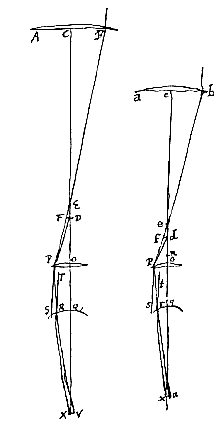 Sunto enim duo diversae longitudinis telescopia lentes exteriores ejusdem generis habentia, quorum alterius lens exterior, quatenus adaperta, sit AB, lens ocularis OP, focis utriusque in idem punctum D compositis; ita enim collocari necesse est ut radij ad oculum paralleli perveniant qui a puncto longinquo ad telescopium feruntur. Sit autem pupilla QR, fundus oculi ad X, centraque omnium C, O, Q, X in eadem recta quae est axis telescopij.
Intelligatur porro refractio radij extremi in lentem AB incidentis esse BEP, quae occurrat lenti oculari in P, cujusque aberratio sit ED, circelli vero aberrationis semidiameter DF. Et jungatur DP, sitque PS axi parallela.
Sunto enim duo diversae longitudinis telescopia lentes exteriores ejusdem generis habentia, quorum alterius lens exterior, quatenus adaperta, sit AB, lens ocularis OP, focis utriusque in idem punctum D compositis; ita enim collocari necesse est ut radij ad oculum paralleli perveniant qui a puncto longinquo ad telescopium feruntur. Sit autem pupilla QR, fundus oculi ad X, centraque omnium C, O, Q, X in eadem recta quae est axis telescopij.
Intelligatur porro refractio radij extremi in lentem AB incidentis esse BEP, quae occurrat lenti oculari in P, cujusque aberratio sit ED, circelli vero aberrationis semidiameter DF. Et jungatur DP, sitque PS axi parallela.