|
Nunc ad aperturas telescopiorum definiendas pergam, ostendamque,
diametros aperturarum in subdupla ratione foci distantiarum lentis exterioris esse ponendos. atque ita quoque foci distantas lentium ocularium.
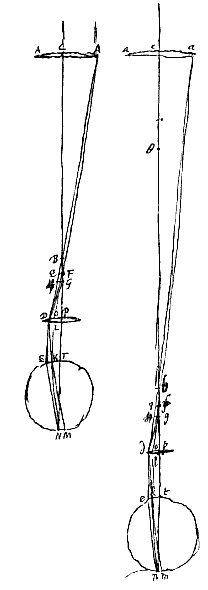 Sit telescopium ex lentibus AC, DP compositum, AC exteriori, DP oculari, axis telescopij per utramque mediam lentem transiens sit CP, qui pupillam oculi secet in T puncto, ejusque fundo occurrat in N. Foci distantia lentis AC sit CF, lentis DP foci distantia PF. dimidiae aperturae latitudo sit AC. Ponatur vero telescopium hoc recte ordinatum, quantum ad lucem ac distinctam visionem attinet, ut nec majorem aperturam in exteriori lente ferre possit, nec acutiorem lentem ocularem; jamque aliud sit construendum, longius ac majoris amplificationis, cujus lens ac, habeat foci distantiamcf, datae rationis ad CF, quaeraturque hinc diameter aperturae aa, itemque foci distantia lentis ocularis pf, quibus fiat aeque lucidem hoc telescopium, et aeque distincte res visas exhibens, atque illud ex lentibus AC, PD.
Sit telescopium ex lentibus AC, DP compositum, AC exteriori, DP oculari, axis telescopij per utramque mediam lentem transiens sit CP, qui pupillam oculi secet in T puncto, ejusque fundo occurrat in N. Foci distantia lentis AC sit CF, lentis DP foci distantia PF. dimidiae aperturae latitudo sit AC. Ponatur vero telescopium hoc recte ordinatum, quantum ad lucem ac distinctam visionem attinet, ut nec majorem aperturam in exteriori lente ferre possit, nec acutiorem lentem ocularem; jamque aliud sit construendum, longius ac majoris amplificationis, cujus lens ac, habeat foci distantiamcf, datae rationis ad CF, quaeraturque hinc diameter aperturae aa, itemque foci distantia lentis ocularis pf, quibus fiat aeque lucidem hoc telescopium, et aeque distincte res visas exhibens, atque illud ex lentibus AC, PD.
Sint omnia ejusdem nominis sed diversae figurae literis utrobique notata, et constructio eadem.
Intelligatur nempe F esse punctum concursus radiorum axi parallelorum qui rubrum colorem adferunt, tam in lentem AC extrinsecus advenientium, quam qui in lentem PD caderent a regione oculi. Sed B esse concursum parallelorum lentis AC, qui violaceum exhibent. G concursum parallelorum qui colorem hunc ducunt per lentem PD. Oculi vero ea sit constitutio, ut radios rubros axi parallelos excipiens perducat ad punctum unum fundi sui. Aberrationem quae ex figura sphaerica oritur pro nulla hic habemus, quippe quae ut jam diximus nullius momenti sit ad hanc quae fit ex coloribus, ac proinde si ab extrema apertura AA ducantur rectae ABD, AFO quae lenti PD occurrant in D et O, eae referent radios coloratos extremos quos ex uno axi parallelo radio fecit refractio lentis AC. Jungantur DF, FA, DG, et productus axis CP secet oculi pupillam in puncto T, ejusque fundo incidat in N. Sitque recta DE axi parallela a lente oculari ad pupillam ducta, et jungatur EN. Caeterum angulus BDF, a cujus magnitudine pendere ostendimus aberrationem in fundo oculi, vocetur angulus aberrationis.
|
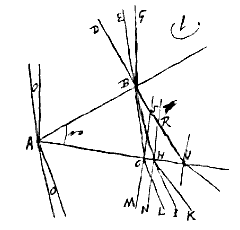 Si sit angulus BAC, quo duo plana angulum ex vitro solidum terminantia inclinantur minor grad. 19.i, sitque praeterea in plano per ABC etiam recta linea DBV, quae planum AB normaliter secet in B, et ad eam inclinentur radij EB, GB, angulis minoribus quam gr. 29 in partem ab A puncto aversam, quorum interior EB intra diaphanum feratur per BH, atque exeat in HK; GB vero feratur intra diaphanum per BC, exeat vero in CL. Dico angulo EBG radiorum incidentium aequalem censeri posse eum quo egressi HK, CL inter se inclinantur, hoc est, angulum KHI, si fiat HI parallela CL.
Si sit angulus BAC, quo duo plana angulum ex vitro solidum terminantia inclinantur minor grad. 19.i, sitque praeterea in plano per ABC etiam recta linea DBV, quae planum AB normaliter secet in B, et ad eam inclinentur radij EB, GB, angulis minoribus quam gr. 29 in partem ab A puncto aversam, quorum interior EB intra diaphanum feratur per BH, atque exeat in HK; GB vero feratur intra diaphanum per BC, exeat vero in CL. Dico angulo EBG radiorum incidentium aequalem censeri posse eum quo egressi HK, CL inter se inclinantur, hoc est, angulum KHI, si fiat HI parallela CL.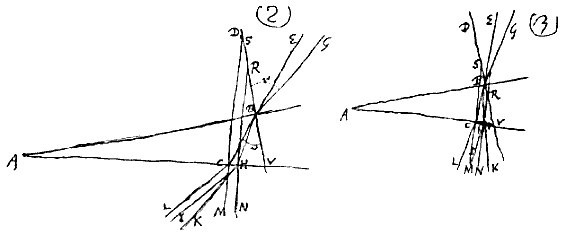
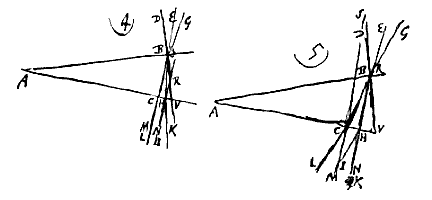
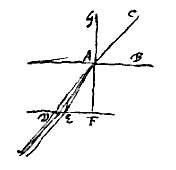 Altera, quod radius in superficiem densioris diaphani oblique incidens, ac velut recta linea habitus, postquam refractus fuerit non amplius in linea feratur, sed velut in plures spargatur exiguis angulis dissidentes, coloribusque infectos. Veluti si in superficiem vitri AB incidat radius CA is refractus spargetur angulo exiguo DAE, cujus latus AD a perpendiculo GAF magis recedens colorem rubrum deferet, alterum extremum AE violaceum obscurum; inter D et E vero apparebunt flavus, viridis, caeruleus, eodem ordine ut in Iride spectari solent.
Altera, quod radius in superficiem densioris diaphani oblique incidens, ac velut recta linea habitus, postquam refractus fuerit non amplius in linea feratur, sed velut in plures spargatur exiguis angulis dissidentes, coloribusque infectos. Veluti si in superficiem vitri AB incidat radius CA is refractus spargetur angulo exiguo DAE, cujus latus AD a perpendiculo GAF magis recedens colorem rubrum deferet, alterum extremum AE violaceum obscurum; inter D et E vero apparebunt flavus, viridis, caeruleus, eodem ordine ut in Iride spectari solent.
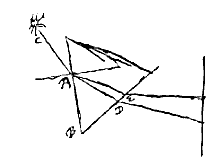
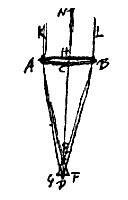 atque hinc porro collegit, in quavis lente vitrea, ut AB, cujus axis CD, si radiorum extremorum axi parallelorum KA, LB pars levius refracta ac rubrum colorem deferens conveniat cum axe in D, maxime vero refracta ac violacea in E, tunc esse ED aequalem 1/50 CD, ac proinde si producantur AE, BE donec occurrant in F et G rectae per D ductae ac lenti AB parallelae, fieri GF, diametrum circelli aberrationis aequalem parti quinquagesimae diametri AB*). Unde et ang. DAF censebitur efficere 1/50 ang.o ADC. Quorum ratio facile apparet posita lente AB planoconvexa, cujus convexa superficies ACB sit a sphaera cujus semidiameter CN. Sicut enim 68 ad 44 ita erit ND ad DC [
atque hinc porro collegit, in quavis lente vitrea, ut AB, cujus axis CD, si radiorum extremorum axi parallelorum KA, LB pars levius refracta ac rubrum colorem deferens conveniat cum axe in D, maxime vero refracta ac violacea in E, tunc esse ED aequalem 1/50 CD, ac proinde si producantur AE, BE donec occurrant in F et G rectae per D ductae ac lenti AB parallelae, fieri GF, diametrum circelli aberrationis aequalem parti quinquagesimae diametri AB*). Unde et ang. DAF censebitur efficere 1/50 ang.o ADC. Quorum ratio facile apparet posita lente AB planoconvexa, cujus convexa superficies ACB sit a sphaera cujus semidiameter CN. Sicut enim 68 ad 44 ita erit ND ad DC [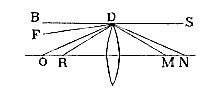 Notandum*) autem Propos. VI [
Notandum*) autem Propos. VI [ Sit telescopium ex lentibus AC, DP compositum, AC exteriori, DP oculari, axis telescopij per utramque mediam lentem transiens sit CP, qui pupillam oculi secet in T puncto, ejusque fundo occurrat in N. Foci distantia lentis AC sit CF, lentis DP foci distantia PF. dimidiae aperturae latitudo sit AC. Ponatur vero telescopium hoc recte ordinatum, quantum ad lucem ac distinctam visionem attinet, ut nec majorem aperturam in exteriori lente ferre possit, nec acutiorem lentem ocularem; jamque aliud sit construendum, longius ac majoris amplificationis, cujus lens ac, habeat foci distantiamcf, datae rationis ad CF, quaeraturque hinc diameter aperturae aa, itemque foci distantia lentis ocularis pf, quibus fiat aeque lucidem hoc telescopium, et aeque distincte res visas exhibens, atque illud ex lentibus AC, PD.
Sit telescopium ex lentibus AC, DP compositum, AC exteriori, DP oculari, axis telescopij per utramque mediam lentem transiens sit CP, qui pupillam oculi secet in T puncto, ejusque fundo occurrat in N. Foci distantia lentis AC sit CF, lentis DP foci distantia PF. dimidiae aperturae latitudo sit AC. Ponatur vero telescopium hoc recte ordinatum, quantum ad lucem ac distinctam visionem attinet, ut nec majorem aperturam in exteriori lente ferre possit, nec acutiorem lentem ocularem; jamque aliud sit construendum, longius ac majoris amplificationis, cujus lens ac, habeat foci distantiamcf, datae rationis ad CF, quaeraturque hinc diameter aperturae aa, itemque foci distantia lentis ocularis pf, quibus fiat aeque lucidem hoc telescopium, et aeque distincte res visas exhibens, atque illud ex lentibus AC, PD.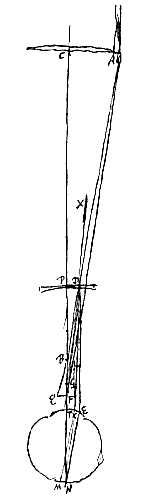 In telescopijs ex convexa et cava lente compositis eadem ostendi possunt, simili plane demonstratione, nisi quod distantia puncti dispersus in lente cava tunc erit quod hic fuit convexi ocularis foci distantia. Sed horum cavorum in compositione jam nullus fere est usus, propter angustiam spatij, quam telescopiorum prospectui relinquunt [
In telescopijs ex convexa et cava lente compositis eadem ostendi possunt, simili plane demonstratione, nisi quod distantia puncti dispersus in lente cava tunc erit quod hic fuit convexi ocularis foci distantia. Sed horum cavorum in compositione jam nullus fere est usus, propter angustiam spatij, quam telescopiorum prospectui relinquunt [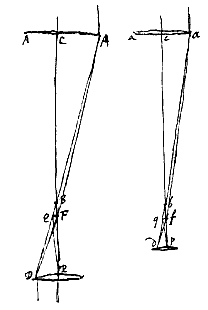 Sint lentium AA, aa aequales foci distantiae CF, et cf ex radijs axi parallelis coloris rubri, itemque aequales CB, cb foci distantiae ex radijs coloris violacei, aperturae autem inaequales quarum diametri AA, aa. eandemque his proportionem habeant lentium ocularium foci distantiae FP, fp. Porro ductis utrobique, ut supra [
Sint lentium AA, aa aequales foci distantiae CF, et cf ex radijs axi parallelis coloris rubri, itemque aequales CB, cb foci distantiae ex radijs coloris violacei, aperturae autem inaequales quarum diametri AA, aa. eandemque his proportionem habeant lentium ocularium foci distantiae FP, fp. Porro ductis utrobique, ut supra [