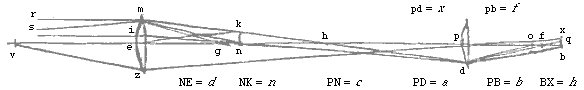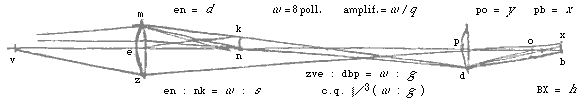[ ... ] examinandum est, an non altera aberratio quae ex figura oboritur aliquid turbare possit. Quem in finem oportet ut utriusque aberrationis angulum in nostro illo quod diximus [<] microscopio, ubi neutram adhuc nocere scimus, primum calculo investigemus. Praemittemus vero Lemma hujusmodi. Lemma 1   Sit lentis convexae PD axis NPB. focus in O, radius axi parallelus SD, qui itaque ex refractione dissipatus mittit radium rubrum in DO, sed violaceum extremum ponamus convenire cum axe in R.

[ 553 ]

[ v ]

Quod si jam a puncto in axe N, feratur in lentem eandem radius ND, qui ex refractione dissipatus, mittat radium rubrum in B, violaceum extremum in F. dico angulum BDF aequalem censeri posse angulo ODR, tantoque propius quanto inclinatio superficierum lentis in D erit minore angulo, quantoque minus distabunt puncta B, O.   Cum enim radius ruber qui inest incidenti radio SD, eat in DO; ruber vero qui in radio ND eat in DB, erit ex propos. [VI] angulus BDO proxime aequalis SDN. Similiterque cum radius violaceus qui inerat in SD, abeat in DR; itemque violaceus qui in ND, abeat in DF; censebitur ex eadem prop. VI ang. FDR aequalis SDN: Itaque aequales inter se censentur et BDO, FDR, et ablato communi FDO erunt similiter aequales BDF, ODR. ac tanto propius quanto et angulus inclinationis superficierum lentis in D erit minoris anguli, et rectiores radij SD, ND in superficies illas incident, radijque ipsi minorem intercipient ang. SDN, ut ex ijs intelligitur quae ad prop. supra dicta fuerunt [<]. patet autem tanto minorem esse SDN quanto punctum B minus distat ab O, tanto enim major PN, quia proportionales sunt BO, BP, BN ex prop [I.XX]. Propositio XVI   Angulum aberrationis ex dissipatione in nostro microscopio, et quantus in Telescopijs et Microscopijs nocere non possit, per calculum inquirere.

[ 555 ]

[ v ]

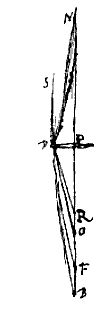
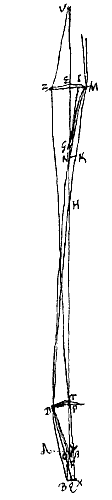Jam calculum quem diximus sic prosequemur. Erat lentis P, cujus crassitudinem pro nulla habemus, foci distantia PO7/10 poll. PD vero 1/20. Jungatur DO. Constat jam, si radius axi parallelus desuper in D incidat, eum spargi debere angulo ODβ, qui sit 1/50 anguli DOP, uti diximus cum radij dissipationem exponeremus [<]. Sit Oβ axi perpendicularis quem secet Dβ in δ. igitur Oβ censebitur 1/50 PD. sed PD erat 1/20 poll. Ergo Oβ1/1000, et OD seu OP, quae erat 7/10, erit ad Oβ, ut 700 ad 1. Sed per lemma praemissum, radius incidens ND dissiparetur angulo qui esset aequalis ODβ. isque angulus esset BDQ, quandoquidem ND ponitur mittere radium rubrum per DB. Itaque ang. BDQODβ. Quia vero vicissim radius incidens BD dissipatur angulo NDK, aequali BDQ ex causa in superioribus explicata [<], hoc est angulo ODβ; erit et DN, seu PN, ad NK, ut DO seu PO ad Oβ, hoc est ut 700 ad 1. Sed EN est ad NP ut 2 ad 7, sive ut 200 ad 700. Ergo EN seu MK ad NK ut 200 ad 1, hoc est ut radius tab. 100000 ad 500 tangentem 17'.12"*); ac proinde angulus aberrationis hujus NMK erit in nostro microscopio proxime 17'.12".   Idemque erit in breviori illo pollicum 41/2 [<], et in omnibus deinceps diminutis, quia haec conditio aberrationis aequalis in investigatione posita fuit. Quod si angulo NMK addamus ang. NMG, quem ibi ob parvitatem negleximus, fiet hic ang. aberrationis 17'.42" circiter°).   *)  Plutôt 17' 10".   °)  En vérité 18' 8" pour le microscope étalon de 121/3 pouces et 18' 43" pour le plus court.

[ 557 ]

[ v ]

Sed in Telescopijs si quaeramus quantus aberrationis hujus angulus fieri possit, inveniemus in nocturnis quidem 31' 1/3 circiter [<], in diurnis vero dimidium sive 15' 2/3. quod ab illis 17'.42" non multum discrepat. Etenim in figura propos. [VII] posita lentis AC foci distantia CF pedum 30, diximus CA esse 3/2 poll. [<] unde FQ1/50 CA, hoc est 3/100 poll. Sed QD seu foci distantia FP tunc erat 3 3/10 poll. Ergo QD ad QF ut 3 3/10 ad 3/100, hoc est ut 110 ad 1, hoc est ut semidiameter circuli 100000 ad 909 tangentem anguli 31'.20", qui est proxime angulus aberrationis QDF, quantum esse diximus.   Ex his intelligitur cur nec in nostro microscopio neque in alio quamlibet breviori eoque magis amplificante, quod secundum inventam regulam ex nostro ordinatum fuerit, haec aberratio ex radij dissipatione nocitura sit. Nunc vero de aberratione quae ex figura lentium sphaerica oritur examen instituamus. Ubi rursus lemma praemittendum est hujusmodi.

[ 559 ]

[ v ]

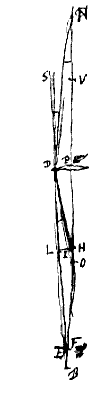Lemma 2 1)   Sit lentis convexae PD axis NPB. Focus in O. Radius axi parallelus SD, qui refractus eat per DH, faciens aberrationem OH, a puncto autem in axe, N, feratur ad lentem eandem radius ND, qui refractus conveniat cum axe in F, sitque B punctum conjugatum ipsi N, adeoque radij ND aberratio FB. Dico HO ad FB fore proxime ut quadratum PO ad quadratum PB tantoque magis quanto distantia NP ad PO comparata major erit.   Sumatur enim PV in axe aequalis PO, sitque HL axi perpend. Et PO sive PV sitc; PDa; NPd; HOn. Jam quia proportionales sunt NV, NP; PO, PB ex prop. [I.XX], erit PBdc/(d - c). Quia vero angulus LDH aequalis censetur SDN ex propos. [VI], hoc est angulo DNP, erit proxime ut NPd, ad PDa, ita DL quae censetur aequalis PH, hoc est c - n, ad LH, quae erit (ac - an)/d. Et quia PD ad LH ut PF ad FH, erit DP minus LH, hoc est (da - ac + an)/d ad DPa, ut PHc - n ad PF, quae erit (dc - dn)/(d - c + n) quae subtracta a PBdc/(d - c) fit FBddn/(dd - 2dc + cc + dn - cn) quae ad HOn, ut dd ad dd - 2dc + cc + dd - cn; haec autem ratio eadem censeri potest quae dd ad dd - 2dc + cc, quia quantitas n minima est caeterarum respectu. Sicut autem dd ad dd - 2dc + cc, hoc est ut quadratum NP ad quadratum NV ita est quadratum PB ad quadratum PO; quia diximus esse ut NV, NP, ita PO ad PB; Ergo erit FB ad HO proxime ut quadratum PB ad quadratum PO, ac tanto quidem magis quanto angulus SDN minor erit, ut patet ex ijs quae ad propos. [VI] annotavimus [<]; hoc est quanto major ratio NP ad PO. Itaque patet propositum.   1)  Voir, sur la question de la validité de ce Lemme, la note 7 de la p. 556.

[ 561 ]

[ v ]

Hinc vero sequitur, Lemma 3   Ductis DO, DB, angulos aequales fore HDO, FDB.   Ponatur enim DO secare HL in I, et FE axi perpendicularem occurrere rectae DB in E. Quia ergo ratio BF ad HO componitur ex rationibus BF ad FE, et FE ad HI et HI ad HO. Hoc est ex rationibus BP ad PD, et FE ad HI, et PD ad PO; hoc est, ex rationibus FE ad HI et BP ad PO. Ratio autem eadem BF ad OH est ea quae quadrati BP ad quadratum PO, ex ante demonstratis [<]; necesse est rationem FE ad HI eandem esse quae BP ad PO, sive quae FP ad PH, quia FB et HO sunt minimae; sive quae FD ad HD. Unde angulus FDE censetur aequalis HDI propter parvitatem angulorum DFP, DHP. Propositio XVII   Angulum aberrationis ex figura in nostro microscopio per calculum investigare.   Hinc ad calculum accedimus in quo jam crassitudo lenticulae P consideranda est, quae sit TP, in figura superiori. Habet autem lenticula haec in nostro microscopio superficiem alteram planam quae deorsum conversa est. Cumque foci distantia PO sit 7/10 pollicis eademque aequalis censeri possit diametro convexitatis superficiei TD [Prop. I.XIV]; erit ut PO, sive 7/10 ad PD1/20, ita haec ad TP, quae fiet 1/280. Hujus vero 7/6 aequantur aberrationi Oδ quam facit radius axi parallelus in D incidens, quia lenticulae plana superficies in partem alteram obversa est. Ergo Oδ7/1680 sive 1/240. Sicut autem δP seu OP ad PD, hoc est, sicut 7/10 ad 1/20, sive ut 14 ad 1, ita est δO ad Oβ. Ergo fit Oβ1/3360; et DO seu PO ad Oβ ut 7/10 ad 1/3360, sive ut 2352 ad 1.

[ 563 ]

Sed per Lemma [3] radius incidens ND faceret angulum aberrationis BDQ aequalem ODβ: ac proinde vicissim radius BD faciet angulum aberrationis NDK aequalem BDQ seu ODβ. Ergo ut DO, seu PO, ad Oβ, hoc est, ut 2352 ad 1, ita erit DN, seu PN, ad NK. Sed ut 2 ad 7, sive ut 672 ad 2352, ita est EN ad NP. Ergo ex aequo EN ad NK, seu MK ad NK, ut 672 ad 1, hoc est ut in Tabulis semidiameter 100000 ad 149, tangentem anguli 5'.8", qui est angulus NMK.   Hic igitur in microscopio nostro est angulus aberrationis ex figura. Quo majorem ferri posse absque visionis incommodo inde apparet, quod inversâ lenticulâ PD, ut pars convexa deorsum spectet, quadruplo fere major sit iste aberrationis angulus;

[ 565 ]

[ v ]

quia tunc aberratio radij qui parallelus axi incideret in D aequat 9/2 crassitudinis PT, ex propos. [II.IV] quae aberratio hic erat tantum 7/6 PT, hoc est fere pars quarta tantum istius. Unde et angulus aberrationis NMK fere quadruplus tunc invenitur ejus qui nunc inventus est 5'. Atqui sic inversâ lenticulâ, vix percipitur aliquid distinctae visioni decedere. Itaque 20 circiter scrupulorum primorum ferri potest angulus istius aberrationis; accedente licet angulo aberrationis quae ex dissipatione, qui erat fere 18' [<]. Semper enim hanc aberrationem alteri superaddi facile intelligi potest.   Quod si in breviori illo 41/2 pollicum microscopio [<], quaeramus eodem modo angulum aberrationis quae ex figura, inveniemus eum quoque 20' circiter; qui proinde vix quoque nocere poterit; ut proinde eximius futurus sit ejusmodi perspicilli effectus. Si vero breviora etiam, ac magis amplificantia moliamur ex praescripto Regulae superius inventae crescet semper iste aberrationis angulus. adeoque haec causa impedit quo minus Regulam istam sequentes, infinito progressu microscopiorum virtutem augere possimus. Sed quod mirum fortasse videbitur, aliam suppetere ostendemus Regulam, per quam ejusmodi progressus concedatur. Praemittimus autem Lemma ejusmodi.

[ 567 ]

[ v ]

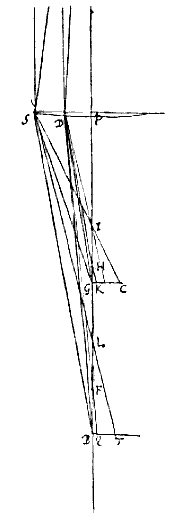Lemma 4   Si in lentem convexam radij incidant axi paralleli, vel a puncto in axe ultra focum distante manantes, efficient ij refracti angulos aberrationis ex Figura, qui proxime triplicatam rationem habeant ejus, quam distantiae punctorum incidentiae ab axe.   Primo vero de parallelis ostendemus.   Sit lentis PS axis PB, focus G, radiorum nempe axi parallelorum ab eoque minimo distantium. Lentis crassitudo pro nulla habeatur, quia tota PS valde exigua intelligitur ad PB comparata. Porro radius parallelus qui in D punctum incidit feratur in DH, faciens aberrationem in GH. qui vero in S incidit parallelus feratur in SI, faciens aberrationem GI. Junctis igitur DG, SG, erunt anguli aberrationis quos hic intelligimus GSI, GDH. Quos dico proxime triplicatam rationem habere ejus quae SP ad DP.   Sit enim GC ad axem perpendicularis, cui occurrant productae DH, SI in K et C. Censentur igitur anguli GSC, KDG eam habere rationem quae CG ad GK, cum DP, SP sint minimae respectu PG. Est autem ratio CG ad KG eadem compositae ex rationibus CG ad GI, et GI ad GH, et GH ad GK. quarum prima ratio CG ad GI, eadem est quae SP ad PI, vel quae SP ad PG, quia IG minima est respectu PG. Item ratio altera GI ad GH est eadem quae quadrati PS ad qu. PD, per prop. [II.VII]. Et tertia GH ad GK eadem quae HP ad PD, hoc est, quae GP ad PD, quia HG est minima respectu GP. Itaque ratio CG ad KG, componetur ex rationibus SP ad PG, et PG ad PD, et quadrati PS ad quadratum PD. Sed harum priores duae efficiunt rationem SP ad PD. Ergo ex tribus composita erit eadem quae cubi SP ad cubum PD. Itaque ostensum est rationem CG ad KG, sive anguli aberrationis CSG ad KDG, proxime esse eam quae cubi SP ad cubum PD, hoc est triplicatam rationis SP ad PD.   Ponamus jam radios incidentes in D et S, venire a puncto cui conjugatum sit punctum B, atque esse radij in D cadentis aberrationem BF; ejus vero qui in S cadit, aberrationem BL. Cum igitur ex lemmate [2] sit ut quadratum PG ad quadratum PB, ita GH ad BF; atque ita quoque IG ad LB, erit permutando, et convertendo, ut IG ad GH ita LB ad BF. Sed IG erat ad GH ut quadratum SP ad quadratum DP, ergo et LB ad BF ut quadratum SP ad quadratum DP.

[ 569 ]

[ v ]

Unde jam, sicut ante de angulis GSI, GDH, ostendetur eadem ratione angulos BSL, BDF esse in ratione triplicata distantiarum SP, PD. Hi enim anguli, sive BST, BDQ censentur esse inter se ut BT ad BQ, quia DP, SP sunt minimae respectu BP. Est autem ratio BT ad BQ eadem compositae ex rationibus TB ad BL, et BL ad BF, et BF ad BQ. Quarum prima TB ad BL est eadem quae SP ad PL, seu quae SP ad PB, quia LB est minima respectu PB. Item ratio altera BL ad BF est eadem quae quadrati PS ad quadratum PD, ut paulo ante est ostensum. Et tertia BF ad BQ est eadem quae FP ad PD, hoc est quae BP ad PD, quia FB est minima respectu BP. Itaque ratio BT ad BQ componetur ex rationibus SP ad PB, et PB ad PD, et quadrati PS ad quadratum PD. quarum duae priores cum efficiant rationem SP ad PD, erit ratio BT ad BQ, hoc est anguli BSL ad BDF, ea quae cubi PS ad cubum PD, quod supererat demonstrandum. Propositio XVIII   Quomodo breviora fieri possint microscopia et magis amplificantia, in quibus servetur eadem claritas et distinctio, nec tamen priori incommodo a majori aberratione ex figura fiant obnoxia. 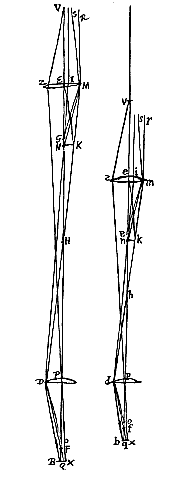*)   Repetatur jam figura quae in inquisitione praecedenti [<], eademque omnia quae ibi leguntur, usque ad ea verba, Nunc vero quia semi-aperturam pd ponox, non autemfa/b post quae sic nunc pergemus.°)   *)  Ed. de Volder & Fullenius, p. 253 [fig.]; cf. p. 553, n. 4.   °)  "erit ex lemmate praemisso", etc. Nous avons cru bien faire de suivre cette indication à l'exemple de de Volder et Fullenius.   { Ponantur bina rursus microscopia, atque omnia eadem quae propositione [XIV], nisi quod incerta sit, in minori, ratio pb ad semiaperturam pd; itemque incerta lentis ocularis foci distantia ne. caetera vero omnia eodem modo construantur. Porro in majori microscopio distantia PB sit b, quâ nempe lenticula P abest a visibili. PNc; NEd. semiaperturae latitudo PDa. BX longitudo rei visaeh, NKn. Ponamus autem distantias punctorum conjugatorum PN ad PB esse in ratione majori quam 6 vel 7 ad 1, et foci distantiam EN majorem esse foci distantiâ PO. quemadmodum haec in hujusmodi microscopijs recte statui solent. at in minori microscopio assumatur distantia pbf ; semiapertura quaesita pdx. Erit autem pncf/b quia proportionales ponimus PB, PN; pb, pn. Quod si fuisset ut BP ad PD ita bp ad pd, apparet futuram pdfa/b, et angulum aberrationis bdq, radij ex n venientis in lentem p, aequalem futurum angulo aberrationis BDQ radij ex N venientis in lentem P: Quia sicut prop. [XIV] ita hic quoque ut NP ad np, ita PB ad pb, et ita quoque foci distantia PO ad po. }

[ 571 ]

Nunc vero quia semi-aperturam pd ponox, non autemfa/b, erit ex lemmate praemisso [<] ut cubus ex fa/b, hoc est, ut f 3a 3/b 3 ad x 3, ita angulus BDQ ad angulum bdq.   Rursus si aequales essent anguli NDK, ndk, censeretur esse NK ad nk ut PN ad pn. Nunc vero ratio NK ad nk componi censebitur ex rationibus PN ad pn, et ea quae anguli NDK ad ndk; hoc est ex rationibus PB ad pb seu b ad f , et anguli BDQ ad bdq; quam diximus esse eandem quae f 3a 3/b 3 ad x 3, sive quae f 3a 3 ad b 3x 3, ac proinde erit NK ad nk ut bf 3a 3 ad fb 3x 3, hoc est ut ffa 3 ad bbx 3. Cumque NK sitn, erit nknbbx 3/ffa 3. Jam quo aberrationis angulus utrobique intra oculum aequalis fiat, deberent esse aequales anguli KMG, kmg; sed pro his ponemus KMN, kmn, neglectis ut supra accessionibus angulorum NMG, nmg, quia exigui prorsus sunt illorum respectu, ac magis etiam quam in disquisitione praecedenti. Sicut igitur NK ad NM seu NE, hoc est sicut n ad d, ita censebitur esse nk ad nm seu ne, hoc est, nbbx 3/ffa 3 ad ne, quae eritdbbx 3/ffa 3.   Jam porro quia eadem longitudo lineolae BX, bx, in dato quidem microscopio spectatur angulo EVZ, in alteram autem angulo evz; debet esse ut angulus EVZ ad evz ita PBD ad pbd. Sic enim lux hausta utroque microscopio erit ut apparens magnitudo, ac proinde eadem utrique claritas. Ergo et permutando, angulus EVZ ad PBD ut evz ad pbd.

[ 573 ]

[ v ]

Ratio autem anguli EVZ ad PBD componitur ex rationibus anguli EVZ ad EPZ seu BPX, et BPX ad PBD; hoc est ex rationibus PE ad EV, seu PN ad NE, et BX ad PD; hoc est ex rationibus c ad d, et h ad a, ac proinde est ea quae ch ad da. Ergo et ratio anguli evz ad pbd debet esse ea quae ch ad da. Haec autem ratio anguli evz ad pbd componitur ex rationibus anguli evz ad epz seu bpx, et bpx ad pbd; hoc est, ex rationibus pe ad ev, seu pn ad ne, et bx ad pd; hoc est, ex rationibus cf/b ad dbbx 3/ffa 3, et h ad x: ac proinde est ea quae hcf/b ad dbbx 4/ffa 3. Igitur eadem ratio ch ad da quae hcf/b ad dbbx 4/ffa 3. Unde fit x 4f 3a 4/b 3. Et x a √√(f 3/b 3).   Quod si jam velimus ut microscopium inventum duplo magis amplificet res visas quam quod erat datum: oportet eandem ob causam, quam exposuimus in praecedenti inquisitione, ut angulus dbp duplo major sit quam DBP, cumque BP ad DP sit ut b ad a, debebit esse bp ad pd, hoc est f ad a √√(f 3/b 3) ut b ad 2a. Unde fit f 1/16 b. atque hinc x, sive a √√(f 3/b 3)1/8 a. Et foci distantia en, quae erat dbbx 3/ffa 31/2 d.   Secundum quae ex nostro microscopio cujus mensuras in priori disquisitione posuimus [<], fiet aliud duplo magis amplificans ratione diametri (servata eadem claritate ac distinctione,) in quo po erit 7/160 poll. en1. distantia np7/16, pb7/144, ev23/7, semidiameter aperturae pd1/160. atque ita ulterius progredi licet ex hujus regulae praescripto, ponendo lenticulae foci distantiam po quamlibet exiguam. nec enim aberratio ex figura, nec obscuritas unquam nocebunt, quippe semper eaedem manentes.

[ 575 ]

[ v ]

neque etiam aberratio altera quae ex radij dissipatione oritur obstabit, cum continue minuatur. Latitudo vero ad pupillam eadem quae in nostro manebit, erat enim ibi ista latitudo eiad/c, ut supra demonstratum [<]. Hic vero quia ut np, hoc est cf/b, ad pd, hoc est a √√f 3 / √√b 3, ita ne, hoc est d √√f / √√b, ad ei, fit rursus eiad/c.   Est igitur ex hac Regula progressio infinita in propagandis microscopij viribus si lenticulas quamlibet exiguas parari posse ponamus.   In hisce vero disquisitionibus eandem semper servari statuimus rationem BP ad PN, quam nempe habent distantiae punctorum conjugatorum ab lente P. Possumus autem et absque eo regulas generales invenire, nonnihil a prioribus diversas, atque eodem tamen tendentes, quas breviter perscribemus, omissa investigandi ratione, ne nimis diutius hic obhaereamus. Nituntur autem ijsdem, quae jam exposuimus, fundamentis.

[ 577 ]

[ v ]

Propositio XIX   Repetita igitur figura Propos. [XIV], si microscopium e duobus convexis e et p compositum quaeratur, quod datam habeat lentis ocularis e foci distantiam, itemque datam amplificationem, et in quo angulus aberrationis ex dissipatione radij, ut et claritas sit eadem quae in alio dato microscopio ex lentibus E et P composito; invenietur foci distantia lenticulae inferioris p, ejusque positus et apertura hoc modo.   Sit lentis ocularis e foci distantia en data aequalis d lineae. postuletur vero ut magnitudo apparens sit ad eam quae ex certa distantia, puta 8 pollicum [<], spectaretur, (quae distantia vocetur ω) ut ω ad q lineam datam. Angulus vero aberrationis, quem diximus esse nmk [<], requiratur aequalis angulo NMK, in altero dato microscopio; quem definimus proportione lineae KM ad KN seu EN ad KN, quae sit ea quae ω ad datam s. ut nempe eandem hanc habeat en ad nk. Claritas denique eadem quoque praestanda sit quae in microscopio dato, quod fiet si, posita rei visae latitudine bx BX, eadem sit ratio anguli zve ad dbp, quae anguli ZVE ad DBP, ut ex superioribus intelligitur [<]. Sit autem haec ratio ea quae ω ad g, quae inde invenitur quod composita sit ex rationibus anguli ZVE ad ZPE seu BPX, et BPX ad PBD; hoc est, ex rationibus PE ad EV, seu PN ad NE (propter proportionales PN, PE, PV), et ratione BX ad PD. Porro BX dicatur h; lenticulae vero quaesitae foci distantia poy; distantia rei visae pbx. Eritque regula hujusmodi y50.sqqdd / (gh. in qu.(q + d)). Cognita vero y invenietur et x quae erit (qy + dy) / d.

[ 579 ]

[ v ]

Semidiameter vero aperturae pd erit 50.dqs / (ωq + ωd). in quibus sciendum est numerum 50 inde esse quod in hac aberratione quae ex dissipatione est ponitur semper BQ1/50 PD, ut in superioribus dictum fuit [<]; pn denique erit(dy + qy) / q. Apparet autem quia hic valor y etiam sic exprimi potest, y 50.sdd / (gh + 2ghd/q + ghdd/qq), quanto minor ponetur q, hoc est quanto major ratio multiplicationis ω ad q, tanto minorem [majorem] fore divisorem quantitatis hujus, ac tanto majorem [minorem] proinde longitudinem y, seu foci distantiam po. atque ita, diminuenda lenticula p, posse quantum libet augeri microscopij virtutem, nisi quatenus altera aberratio obstabit, quae ex figura superficiei sphaericae pendet, cui paulo post aliam regulam applicabimus.   Sed si datam ponamus lenticulam p, non autem ocularem e, inveniemus non posse tunc augeri amplificationem nisi paulo tantum. Si enim foci distantia data po vocetur r, caeteris eadem, quae prius significantibus, invenitur xx 50.qqrs / hg. ubi apparet, quanto minor ponetur q, hoc est, quo major ratio amplificationis ω ad q, eo minorem fieri x.

[ 581 ]

[ v ]

atqui x, seu pb, debet esse major quam r, seu po. Ergo si in hujusmodi microscopio ponatur ab initio pb minor quam dupla po; (ut omnino faciendum, et in nostro superius descripto [<] est pb ad po tantum ut 10 ad 9) non poterit q duplo minor quam prius adsumi; hoc est, non poterit duplicari ampliatio, quia x fieret dimidia prioris, ac proinde minor quam r.   Omnis igitur microscopij hujusmodi perfectio in lenticulae inferioris parvitate quaerenda est; computando ex praescripto regulae modo traditae, quoad aberratio ex figura non oberit; hoc est, quoad ejus angulus NMK infra 20' consistet [<]. Sed si major ampliatio postuletur, oportet ex dato microscopio in quo angulus hic non erit major quam 20', invenire aliud ex regula, quae est hujusmodi, y 6d 4q 4s / (7gh 3 in.qu.qu.(q + d)), ubi rursus erit x(qy + dy)/d, pn(dy + qy)/q, sed pd fit hic √ 3 (6sqdy 2 / 7(ωq + ωd)). Et sciendum est insuper rationem anguli ZVE ad DBP in microscopio dato eam nunc poni quae √ 3ω ad √ 3g. Atque hoc modo quousque lubet diminui potest q, hoc est, augeri amplificatio, manente lente oculari eadem, nec non distincta visione et claritate, sed magis decrescet lenticulae foci distantia. Numerus autem 6/7 quantitati huic praepositus inde oritur quod lenticulam p planoconvexam ponimus, superficie plana deorsum spectante; cujus aberratio ex figura pertinens ad radium extremum axi parallelum, est 7/6 suae crassitudinis, ut ante hoc ostensum [<]. Sic si utrimque aequaliter convexa lenticula p poneretur, esset numerus praefixus 3/5, quia aberratio ejusmodi lentis efficit 5/3 suae crassitudinis [<].

[ 583 ]

[ v ]

Caeterum ut utriusque regulae exemplum demus, ac primo prioris, ubi y 50.sqqdd / (gh. in qu.(q + d)), sciendum est hinc incipiendum, ut lineae s et g inveniantur quantae sunt in microscopio dato. ac fit quidem s1/25 poll. quia ibi ratio EN seu MK ad NK, hoc est ω ad s, fuit inventa quae 200 ad 1 [<]. Ponitur enim ω8 poll. et ut 200 ad 1, ita 8 ad 1/25. at g invenitur16/7, quia ratio ω ad g dicta fuit componi ex rationibus PN ad NE, et BX ad PD; quae composita redit ad solam rationem PN ad NE, sive 7 ad 2, si BX seu h (quod licet) ponatur aequalis PD, quae ibi erat 1/20. nam ut 7 ad 2 ita est 8 ad 16/7. quaecunque vero ponatur h erit semper quantitas gh eadem in dato microscopio. Quod si jam d eandem esse ponamus in eo quod quaerimus, quae erat in nostro [<], nempe d2; sed rationem amplificationis ω ad q eam velimus esse quae 72 ad 1, hoc est duplo majorem quam in nostro, unde q fit1/9; ex his jam secundum regulam, invenietur y70/361, et reliqua prout fuere in expositione regulae definita. Quod si his ijsdem positis, statuatur d1 poll. invenitur y7/40 et pd 1/40, prorsus ut in priori disquisitione, ubi servabatur ratio eadem BP ad PN [<]; quod veritatem regulae hujus comprobat.   In posteriori regula ubi y 6d 4q 4s / (7gh 3 in.qu.qu.(d + q)) quaesitis prius s et g quantae sunt in dato microscopio, habita ratione aberrationis ex figura, invenitur quidem s1/84 poll. quia ibi ratio EN seu MK ad NK, hoc est, ω ad s, fuit inventa quae 672 ad 1 [<]; nam ut 672 ad 1 ita ω seu 8 ad 1/84.

at g invenitur64/343, quia ratio √ 3ω ad √ 3g hoc est ratio anguli ZVE ad DBP, dicta fuit componi ex rationibus PN ad NE et BX ad PB [PD], quae composita redit, ut paulo ante, ad rationem solam PN ad NE, seu 7 ad 2. Ut autem 7 ad 2 ita √ 3ω seu 2, ad 4/7; quod ergo aequale √ 3g, ideoque g64/343. quaecunque vero ponatur h, erit hic semper in microscopio dato eadem quantitas gh 3. Quod si jam d eandem esse velimus in microscopio quaesito ac in dato nostro, nempe d2 poll., rationem vero amplificationis ω ad q duplam nostrae, hoc est, quae 72 ad 1; erit q1/9; et ex his jam secundum hanc regulam invenietur y proxime1/19. Et reliqua ut fuere in expositione regulae definita. Quod si his ijsdem positis, statuatur d1 poll. invenietur y7/160 et pd1/160 prorsus ut in secunda superiori disquisitione [<], ubi servabatur ratio BP ad PN, quod posterioris hujusce regulae veritatem comprobat. [ Finis partis tertiae. ]