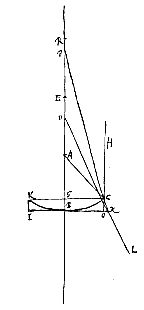
 At in eadem lente contrario modo collocata, ut nempe superficies cava KBC radios parallelos excipiat, duae sunt radiorum refractiones, radius enim HC primum in C frangitur, ferturque inde secundum Cκ, quae retro producta cum axe convenit in P, ac rursus ex plana superficie egrediens in κ pergit secundum κL, quae retro producta convenit cum axe citra punctum P, puta in D. Est autem distantia BE puncti dispersus lentis sic positae dupla rursus BA: Inveniturque aberratio radij extremi ED hoc pacto.
At in eadem lente contrario modo collocata, ut nempe superficies cava KBC radios parallelos excipiat, duae sunt radiorum refractiones, radius enim HC primum in C frangitur, ferturque inde secundum Cκ, quae retro producta cum axe convenit in P, ac rursus ex plana superficie egrediens in κ pergit secundum κL, quae retro producta convenit cum axe citra punctum P, puta in D. Est autem distantia BE puncti dispersus lentis sic positae dupla rursus BA: Inveniturque aberratio radij extremi ED hoc pacto.
Primum refractio radij HC facta in superficie cava KBC nempe Cκ in eandem rectam convenit cum refractione radij OC axi lentis paralleli si superficies CBK convexa foret, adeoque invenietur AP intervallum quo distat concursus productae Cκ, a centro A, eodem modo atque supra in lente planoconvexa [<]; estque hic rursus AP ad PC ut 2 ad 3. Ergo et PC dabitur. Sicut autem GP ad PC ita BP ad Pκ. Ergo et haec data erit, et ex eadem triangulorum similitudine dabitur et Bκ. Jam vero cum secunda refractione radius Cκ ita inflectatur in κL, ut, concurrente ea cum axe in D, ratio Pκ ad κD sit eadem quae refractiones vitri metitur, nempe quae 3 ad 2; dataque sit Pκ. etiam κD dabitur, a cujus quadrato auferendo quadr. Bκ, habebitur quadr. BD, unde et ipsa BD, ac proinde et DE.
Est autem sicut in lente planoconvexa, cujus sphaerica superficies exterior ponitur, ita et in hac lentis concavoplanae positione, aberratio ED proxime 7/6 crassitudinis CO sive GB.
Adeo ut hoc modo longe melius radios parallelos haec lens cava dispergere dicenda sit quam cum superficie plana illos primum excipit.
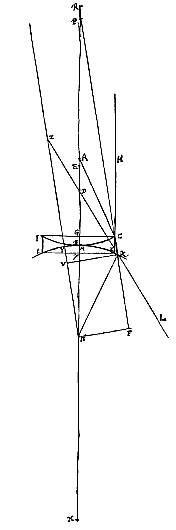 Esto autem jam lens utrinque cava IBCKBι. Sitque superficiei IBC, quae parallelos radios excipit, centrum A alterius vero superficiei ιBK centrum N. per quae transiens axis lentis NA utrimque productus intelligatur. datis igitur semidiametris AB, NM, dabitur et BE distantia puncti dispersus radiorum parallelorum. factis enim BR tripla BA, et MX tripla MN, constat esse ut RX ad RN ita RB ad RE {* Prop. I.I}; unde RE, ac proinde et EB, datum esse liquet.
Esto autem jam lens utrinque cava IBCKBι. Sitque superficiei IBC, quae parallelos radios excipit, centrum A alterius vero superficiei ιBK centrum N. per quae transiens axis lentis NA utrimque productus intelligatur. datis igitur semidiametris AB, NM, dabitur et BE distantia puncti dispersus radiorum parallelorum. factis enim BR tripla BA, et MX tripla MN, constat esse ut RX ad RN ita RB ad RE {* Prop. I.I}; unde RE, ac proinde et EB, datum esse liquet.
Ponamus porro radium extremum HC, axi parallelum, post refractionem primam in superficie IBC, ita ferri secundum Cκ, ut, retro productus, conveniat cum axe in P. Altera vero refractione, in superficie ιMK, flecti eum secundum κL, quae retro producta conveniat cum axe in D. Aberratio itaque radij extremi HC est DE, quam paulo alia ratione hic inveniri ostendemus quam in lente utrinque convexa [<]. Sed prius animadvertendum est, licet superficies ιMK ad κ producta intelligatur, atque ita paulo amplius pateat quam superficies IBC, crassitudinem tamen lentis eam hic statui Gγ quae est aequalis CK parti nimirum rectae HC inter superficiem utramque interceptae. sicut et apertura lentis dupla CG censenda est, non vero distantia dupla ab axe puncti κ.
Sit jam NZ parallela CP; atque ei occurrat producta κD in Z. ducatur deinde κV perpendicularis ad NZ, et NF ad Pκ productam.
|
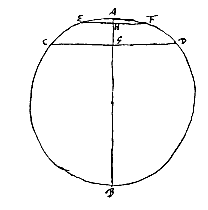 Sint ejusdem circuli exigua segmenta CAD, EAF, quae utraque diameter circuli AB bifariam secet, sintque segmentorum altitudines AG, AH, dico rationem AG ad AH proxime eandem esse, quae quadrati baseos CD ad quadr. baseos EF. Quia enim rectangulum BGA aequale quadrato GD: et rectangulum BHA aequale quadrato FH; apparet esse sicut quadratum GD ad qu. HF, sive ut qu. CD ad qu. EF ita rectangulum BGA ad rectangulum BHA; sicut autem rectangulum BGA ad rectangulum BG, HA, quod pauxillo minus est rectangulo BHA, ita est AG ad AH. Ergo et AG ad AH exiguo majorem rationem habet quam quadratum CD ad qu. EF.
Sint ejusdem circuli exigua segmenta CAD, EAF, quae utraque diameter circuli AB bifariam secet, sintque segmentorum altitudines AG, AH, dico rationem AG ad AH proxime eandem esse, quae quadrati baseos CD ad quadr. baseos EF. Quia enim rectangulum BGA aequale quadrato GD: et rectangulum BHA aequale quadrato FH; apparet esse sicut quadratum GD ad qu. HF, sive ut qu. CD ad qu. EF ita rectangulum BGA ad rectangulum BHA; sicut autem rectangulum BGA ad rectangulum BG, HA, quod pauxillo minus est rectangulo BHA, ita est AG ad AH. Ergo et AG ad AH exiguo majorem rationem habet quam quadratum CD ad qu. EF.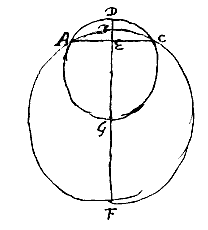 Sint segmenta exigua inaequalium circulorum, ABC, ADC, eandem basin AC habentia, ac bifariam divisa recta DE; in qua diametri circulorum, BF quidem ejus ex quo segmentum ABC, DG vero minoris ex quo segmentum ADC. Dico sicut BF ad DG ita proxime esse altitudinem DE ad BE. Cum enim rectangula FEB, GED inter se aequalia sint, quippe quae singula aequentur quadrato EC, Erit proinde ut FE ad GE ita DE ad EB. Sed ut FE ad GE, ita est proxime diameter FB ad diametrum GD, cum partes EB, ED minimae ponantur totarum diametrorum respectu. Ergo etiam ut diameter FB ad diam. GD ita est proxime DE ad altitudinem BE.
Sint segmenta exigua inaequalium circulorum, ABC, ADC, eandem basin AC habentia, ac bifariam divisa recta DE; in qua diametri circulorum, BF quidem ejus ex quo segmentum ABC, DG vero minoris ex quo segmentum ADC. Dico sicut BF ad DG ita proxime esse altitudinem DE ad BE. Cum enim rectangula FEB, GED inter se aequalia sint, quippe quae singula aequentur quadrato EC, Erit proinde ut FE ad GE ita DE ad EB. Sed ut FE ad GE, ita est proxime diameter FB ad diametrum GD, cum partes EB, ED minimae ponantur totarum diametrorum respectu. Ergo etiam ut diameter FB ad diam. GD ita est proxime DE ad altitudinem BE.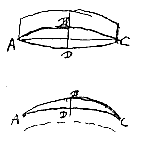 Crassitudo lentis convexae
Crassitudo lentis convexae 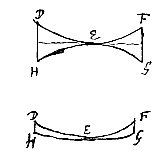 Crassitudo autem lentis cavae
Crassitudo autem lentis cavae 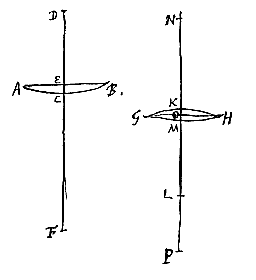 Sit primo lentium altera AB planoconvexa, sitque superficiei ACB semidiam. convexitatis DC. crassitudo lentis CE, foci distantia CF, quae erit dupla CD [
Sit primo lentium altera AB planoconvexa, sitque superficiei ACB semidiam. convexitatis DC. crassitudo lentis CE, foci distantia CF, quae erit dupla CD [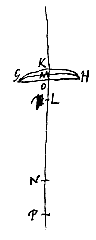
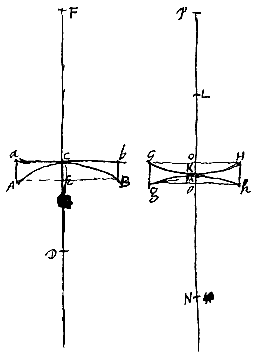 Sit jam etiam lens planocava ACBba superficie utraque contigua in C; sitque rursus superficiei ACB centrum D, et CF distantia puncti dispersus, quae est dupla CD [
Sit jam etiam lens planocava ACBba superficie utraque contigua in C; sitque rursus superficiei ACB centrum D, et CF distantia puncti dispersus, quae est dupla CD [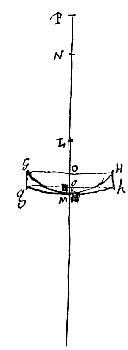 Lens autem altera, vel utrimque cava vel cavoconvexa [convexoconcava] sit GKHhMg aequalem ipsi AB latitudinem habens, punctique dispersus distantiam PM aequalem FC. Harum autem lentium superficies utraeque sese in puncto medio contingere ponuntur, ita ut puncta K et M in unum conveniant, ac crassitudo lentis sit, vel summa duarum KO, Mo, quae altitudines utriusque sphaericae superficiei referunt, vel earum differentia. Quae crassitudo ut aequalis ostendatur crassitudini CE lentis ACBba, repetenda tantum est utraque praecedens demonstratio, quarum prior convenit lenti utrimque cavae, posterior cavoconvexae [convexoconcavae], ubi observandum tamen ut pro foci distantia semper legatur distantia puncti dispersus, et animadvertendum summam aut differentiam duarum KO, Mo, hic esse Oo, cum illic fuerit KM.
Lens autem altera, vel utrimque cava vel cavoconvexa [convexoconcava] sit GKHhMg aequalem ipsi AB latitudinem habens, punctique dispersus distantiam PM aequalem FC. Harum autem lentium superficies utraeque sese in puncto medio contingere ponuntur, ita ut puncta K et M in unum conveniant, ac crassitudo lentis sit, vel summa duarum KO, Mo, quae altitudines utriusque sphaericae superficiei referunt, vel earum differentia. Quae crassitudo ut aequalis ostendatur crassitudini CE lentis ACBba, repetenda tantum est utraque praecedens demonstratio, quarum prior convenit lenti utrimque cavae, posterior cavoconvexae [convexoconcavae], ubi observandum tamen ut pro foci distantia semper legatur distantia puncti dispersus, et animadvertendum summam aut differentiam duarum KO, Mo, hic esse Oo, cum illic fuerit KM.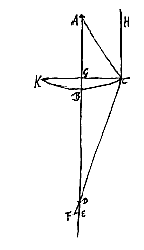
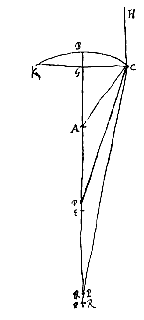
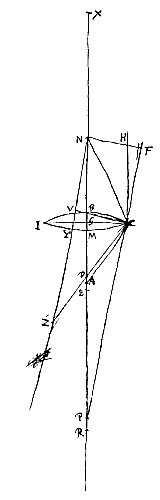 Esto jam proposita lens utrinque convexa IC, sitque superficiei IBC, quae radios parallelos excipit, centrum A; superficiei vero IMC centrum N, per quae transiens axis lentis NA utrimque productus sit. datas autem ponimus semidiametros AB, NM, et semidiametrum lentis GC. Jam si E ponatur focus esse lentis IC et sumatur BR tripla BA et MX tripla MN, debebit esse ut RX ad RN ita RM ad RE [
Esto jam proposita lens utrinque convexa IC, sitque superficiei IBC, quae radios parallelos excipit, centrum A; superficiei vero IMC centrum N, per quae transiens axis lentis NA utrimque productus sit. datas autem ponimus semidiametros AB, NM, et semidiametrum lentis GC. Jam si E ponatur focus esse lentis IC et sumatur BR tripla BA et MX tripla MN, debebit esse ut RX ad RN ita RM ad RE [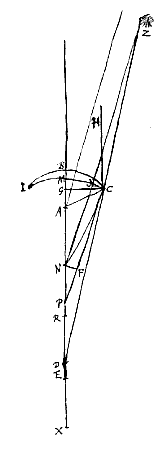
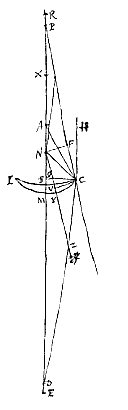 Secundum quae et menisci quilibet inter se et cum lentibus utrimque convexis comparari possunt. Ut si, exempli gratia, in priore casu, ponatur superficiei cavae semidiameter NM tripla semidiametri AB, hoc est, a
Secundum quae et menisci quilibet inter se et cum lentibus utrimque convexis comparari possunt. Ut si, exempli gratia, in priore casu, ponatur superficiei cavae semidiameter NM tripla semidiametri AB, hoc est, a 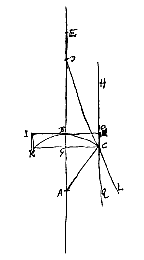 Sit primum lens planoconcava KBCOI, superficie plana OI radios parallelos excipiente, centrum vero superficiei concavae sit A, axis lentis ABE; radius autem axi parallelus extremus sit HO, qui planam quidem superficiem irrefractus transibit. ex cava autem egrediens ita frangatur ut pergat secundum CL, quae retro producta conveniat cum axe in D. Punctum autem dispersus lentis sit E, quod invenitur ponendo BE duplam BA, ut constat ex propos. [I.
Sit primum lens planoconcava KBCOI, superficie plana OI radios parallelos excipiente, centrum vero superficiei concavae sit A, axis lentis ABE; radius autem axi parallelus extremus sit HO, qui planam quidem superficiem irrefractus transibit. ex cava autem egrediens ita frangatur ut pergat secundum CL, quae retro producta conveniat cum axe in D. Punctum autem dispersus lentis sit E, quod invenitur ponendo BE duplam BA, ut constat ex propos. [I. At in eadem lente contrario modo collocata, ut nempe superficies cava KBC radios parallelos excipiat, duae sunt radiorum refractiones, radius enim HC primum in C frangitur, ferturque inde secundum Cκ, quae retro producta cum axe convenit in P, ac rursus ex plana superficie egrediens in κ pergit secundum κL, quae retro producta convenit cum axe citra punctum P, puta in D. Est autem distantia BE puncti dispersus lentis sic positae dupla rursus BA: Inveniturque aberratio radij extremi ED hoc pacto.
At in eadem lente contrario modo collocata, ut nempe superficies cava KBC radios parallelos excipiat, duae sunt radiorum refractiones, radius enim HC primum in C frangitur, ferturque inde secundum Cκ, quae retro producta cum axe convenit in P, ac rursus ex plana superficie egrediens in κ pergit secundum κL, quae retro producta convenit cum axe citra punctum P, puta in D. Est autem distantia BE puncti dispersus lentis sic positae dupla rursus BA: Inveniturque aberratio radij extremi ED hoc pacto. Esto autem jam lens utrinque cava IBCKBι. Sitque superficiei IBC, quae parallelos radios excipit, centrum A alterius vero superficiei ιBK centrum N. per quae transiens axis lentis NA utrimque productus intelligatur. datis igitur semidiametris AB, NM, dabitur et BE distantia puncti dispersus radiorum parallelorum. factis enim BR tripla BA, et MX tripla MN, constat esse ut RX ad RN ita RB ad RE {* Prop.
Esto autem jam lens utrinque cava IBCKBι. Sitque superficiei IBC, quae parallelos radios excipit, centrum A alterius vero superficiei ιBK centrum N. per quae transiens axis lentis NA utrimque productus intelligatur. datis igitur semidiametris AB, NM, dabitur et BE distantia puncti dispersus radiorum parallelorum. factis enim BR tripla BA, et MX tripla MN, constat esse ut RX ad RN ita RB ad RE {* Prop. 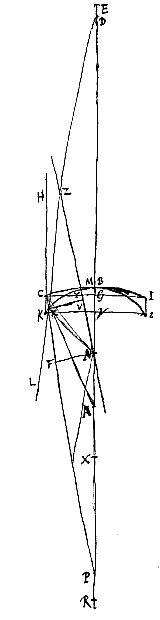 Secundum haec omnes lentes utrimque cavae inter se comparari possunt, ac quanto quaeque melius radios dispergat reperiri. Optima autem ex minimi determinatione invenietur, quae hic necessario eadem est atque in lente utrimque convexa; ut nempe ratio a ad n, hoc est semidiametri AB ad NM sit ea quae 1 ad 6. Adeo ut hujusmodi lens ad corrigendam myopum visionem [
Secundum haec omnes lentes utrimque cavae inter se comparari possunt, ac quanto quaeque melius radios dispergat reperiri. Optima autem ex minimi determinatione invenietur, quae hic necessario eadem est atque in lente utrimque convexa; ut nempe ratio a ad n, hoc est semidiametri AB ad NM sit ea quae 1 ad 6. Adeo ut hujusmodi lens ad corrigendam myopum visionem [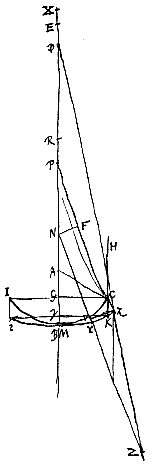 Regula ad inveniendam aberrationem radij extremi ED, priori casu erit ista,
Regula ad inveniendam aberrationem radij extremi ED, priori casu erit ista,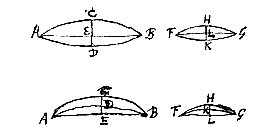 Crassitudines lentium hujusmodi esse inter se sicut quadrata latitudinum, facile ostenditur ex demonstratis propos. [
Crassitudines lentium hujusmodi esse inter se sicut quadrata latitudinum, facile ostenditur ex demonstratis propos. [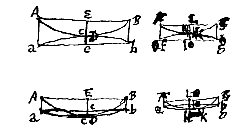 In lentibus utrimque cavis, quarum superficies ACB, aDb sese contingere ponuntur, itemque FKG, fKg; quarumque crassitudines Ee et Ll, eadem est demonstratio, quae in utrinque convexis. Et in cavoconvexis [convexoconcavis], eadem quae in meniscis. Quod si vero vel convexarum vel cavarum lentium altera superficies plana fuerit, manifesta ex his quae dicta sunt est demonstratio.
In lentibus utrimque cavis, quarum superficies ACB, aDb sese contingere ponuntur, itemque FKG, fKg; quarumque crassitudines Ee et Ll, eadem est demonstratio, quae in utrinque convexis. Et in cavoconvexis [convexoconcavis], eadem quae in meniscis. Quod si vero vel convexarum vel cavarum lentium altera superficies plana fuerit, manifesta ex his quae dicta sunt est demonstratio.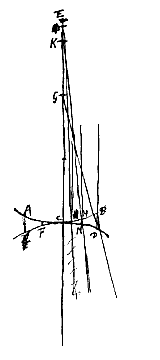 In cavis lentibus facilior hujus rei est demonstratio pendetque a proxime praecedenti. Sit enim lens cava ACBDCF cujus axis CE: punctum dispersus E. Radiusque axi parallelus in B punctum incidens ita dispergatur ut retro productus conveniat cum axe in G. alius vero radius parallelus axi, sed propinquior incidens in H punctum dispergatur, ita ut productus retro conveniat cum axe in K. Ut igitur appareat aberrationem EG esse ad EK sicut quadr. distantiae puncti B ab axe, ad quadr. distantiae puncti H, considerandum est ita se rem habere ac si sint lentes duae diversae DBA, NHF, quarum dimidiae latitudines sint dictae distantiae punctorum B et H ab axe. Cumque sphaericae superficies utrique lenti sint eaedem, patet ex prop. praecedenti crassitudines earum BD, HN, ita esse inter se sicut quadrata illarum dimidiarum latitudinum. Sicut autem crassitudines BD, HN, ita sunt inter se et aberrationes EG, EK. Ergo et harum ratio eadem est quae quadratorum a distantijs punctorum B et H ab axe.
In cavis lentibus facilior hujus rei est demonstratio pendetque a proxime praecedenti. Sit enim lens cava ACBDCF cujus axis CE: punctum dispersus E. Radiusque axi parallelus in B punctum incidens ita dispergatur ut retro productus conveniat cum axe in G. alius vero radius parallelus axi, sed propinquior incidens in H punctum dispergatur, ita ut productus retro conveniat cum axe in K. Ut igitur appareat aberrationem EG esse ad EK sicut quadr. distantiae puncti B ab axe, ad quadr. distantiae puncti H, considerandum est ita se rem habere ac si sint lentes duae diversae DBA, NHF, quarum dimidiae latitudines sint dictae distantiae punctorum B et H ab axe. Cumque sphaericae superficies utrique lenti sint eaedem, patet ex prop. praecedenti crassitudines earum BD, HN, ita esse inter se sicut quadrata illarum dimidiarum latitudinum. Sicut autem crassitudines BD, HN, ita sunt inter se et aberrationes EG, EK. Ergo et harum ratio eadem est quae quadratorum a distantijs punctorum B et H ab axe. 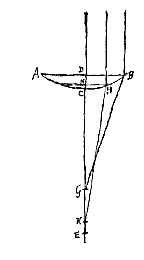
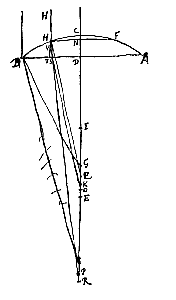 Ponatur radius extremus axi parallelus incidens in B, convenire cum axe in G, adeo ut aberratio ejus sit EG, radius vero parallelus incidens in punctum H, feratur inde secundum rectam HP quae secet superficiem AB in S, ubi facta altera refractione, conveniat cum axe in K, adeo ut aberratio radij hujus sit EK. Ostendendum est igitur, quod sicut quadr. BD ad quadr. HN ita aberratio EG ad EK. Ducatur HQ parallela SK; atque occurrat axi in Q. Sit etiam HT parallela axi CD, quae superficiei AB occurrat in T; ac denique producta KS occurrat ipsi HT in V.
Ponatur radius extremus axi parallelus incidens in B, convenire cum axe in G, adeo ut aberratio ejus sit EG, radius vero parallelus incidens in punctum H, feratur inde secundum rectam HP quae secet superficiem AB in S, ubi facta altera refractione, conveniat cum axe in K, adeo ut aberratio radij hujus sit EK. Ostendendum est igitur, quod sicut quadr. BD ad quadr. HN ita aberratio EG ad EK. Ducatur HQ parallela SK; atque occurrat axi in Q. Sit etiam HT parallela axi CD, quae superficiei AB occurrat in T; ac denique producta KS occurrat ipsi HT in V.