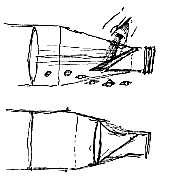
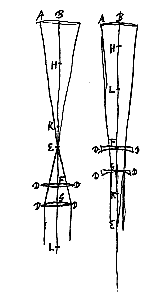
 His inquam positis, accipienda est dicta distantia EG a puncto E versus lentem A ponendaque lens cava in puncto G; vel eadem distantia accipienda versus alteram partem a puncto E, atque in termino G ponenda lens convexa. Sic enim utroque casu fiet ut penetrata lente DD radij paralleli ad oculum perveniant, ut constat ex prop. [I.XVI et XVII] atque ita distincta continget visio ei qui bona est oculi formatione.
His inquam positis, accipienda est dicta distantia EG a puncto E versus lentem A ponendaque lens cava in puncto G; vel eadem distantia accipienda versus alteram partem a puncto E, atque in termino G ponenda lens convexa. Sic enim utroque casu fiet ut penetrata lente DD radij paralleli ad oculum perveniant, ut constat ex prop. [I.XVI et XVII] atque ita distincta continget visio ei qui bona est oculi formatione.Si vero myopi aptandum sit idem perspicillum qui visibile ad distantiam FH demum distincte cernere possit, sumatur FL*) aequalis distantiae GE, qua focus suus aut punctum dispersus abest a lente DD, haec enim data est; Et auferatur quidem FL ab FH si lens DD cava sit, addatur vero si convexa. Et ut HL ad LF ita sit LF ad aliam. dico huic aequale sumendum esse intervallum GF secundum quod minuenda est utroque casu longitudo perspicilli, quae prius erat GB, ut myopi conveniat.
Posita enim lente DD in F et sumta FK aequali FL. quia HL ad LF ut LF ad FG, sive ut FK ad KE; erit et HF ad FL sive FK ut FE ad EK: Et permutando HF ad FE ut FK ad KE, quare et HE ad EF ut FE ad EK. Cum itaque punctum E sit ad quod vel a quo tendentes radij occurrant lenti DD; punctum vero K sit illud, quo pertinent refractiones parallelorum a parte opposita venientium; sequitur radios ad E vel ab E venientes ita flecti a lente DD, ut inde ferantur tanquam egressi a puncto H. Unde recte se habebit perspicillum ad distinctam visionem myopi praestandam.
*) Plus tard Huygens ajouta en marge: "non definivisti punctum F."
En effet, pour exécuter la construction indiquée on doit faire une figure à part.
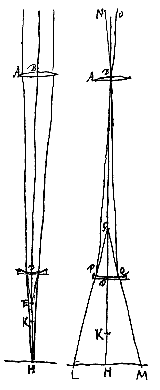
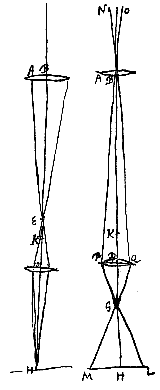 Sit igitur lens convexa AB soli obversa, cujus focus E punctum. Altera vero in D concava vel convexa, nam utraque telescopij forma huic rei idonea est, et magis quidem quae duorum est convexorum, quoniam picturas erectas exhibet, cum altera invertat. Lentis autem D sit K punctum concursus vel dispersus radiorum parallelorum a parte [qua est] H venientium. sitque in H constituta tabula alba ad excipiendam solis imaginem. Quae igitur ut distincta ac terminata appareat, oportet radios qui ab uno solis puncto procedunt, hoc est, qui paralleli inter se deferuntur in lentem AB, in uno rursus tabulae puncto colligi. Quapropter paulo major debet esse distantia lentium AB et D quam in constitutione telescopij media, sive quae bene videnti fuerit accommodata; ac talis requiritur positio lentis D, ut in continua sint proportione EK, ED, EH. Sic enim fiet ut radij tendentes ad E, focum lentis AB, deducantur ad punctum H. at in telescopij constitutione media congruere debet punctum K foco E, ut superius est ostensum [
Sit igitur lens convexa AB soli obversa, cujus focus E punctum. Altera vero in D concava vel convexa, nam utraque telescopij forma huic rei idonea est, et magis quidem quae duorum est convexorum, quoniam picturas erectas exhibet, cum altera invertat. Lentis autem D sit K punctum concursus vel dispersus radiorum parallelorum a parte [qua est] H venientium. sitque in H constituta tabula alba ad excipiendam solis imaginem. Quae igitur ut distincta ac terminata appareat, oportet radios qui ab uno solis puncto procedunt, hoc est, qui paralleli inter se deferuntur in lentem AB, in uno rursus tabulae puncto colligi. Quapropter paulo major debet esse distantia lentium AB et D quam in constitutione telescopij media, sive quae bene videnti fuerit accommodata; ac talis requiritur positio lentis D, ut in continua sint proportione EK, ED, EH. Sic enim fiet ut radij tendentes ad E, focum lentis AB, deducantur ad punctum H. at in telescopij constitutione media congruere debet punctum K foco E, ut superius est ostensum [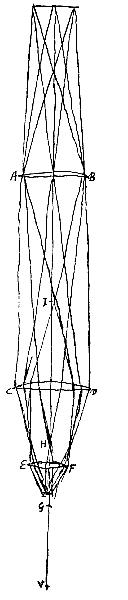
 Esto igitur lens magna sive exterior AB, quae foci distantiam habeat LG, sive ea sit duorum aut trium pedum tantum, aut etiam 6 vel 10 vel 20, possumus enim ad omnes has ijsdem ocularibus uti, hae vero sint EF, CD, quarum posterioris foci distantia KT quadrupla sit, vel paulo minus, foci distantiae lentis EF quae sit SH. Et haec quidem duos pollices non excedat. latitudo CD sit 31/2 poll. EF duplo minor*). Intervallum SK inter utramque lentem sit circiter duplum SH. Ita vero cum lente exteriori AB componantur ut hujus focus G cadat inter lentem EF et focum ejus H, atque sint proportionales GT, GK, GH.
Esto igitur lens magna sive exterior AB, quae foci distantiam habeat LG, sive ea sit duorum aut trium pedum tantum, aut etiam 6 vel 10 vel 20, possumus enim ad omnes has ijsdem ocularibus uti, hae vero sint EF, CD, quarum posterioris foci distantia KT quadrupla sit, vel paulo minus, foci distantiae lentis EF quae sit SH. Et haec quidem duos pollices non excedat. latitudo CD sit 31/2 poll. EF duplo minor*). Intervallum SK inter utramque lentem sit circiter duplum SH. Ita vero cum lente exteriori AB componantur ut hujus focus G cadat inter lentem EF et focum ejus H, atque sint proportionales GT, GK, GH. 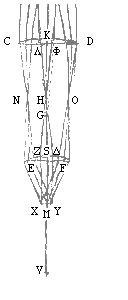 Ratio autem AB ad XY sive ad ZΔ, componitur ex rationibus AB ad ΛΦ et ΛΦ ad ZΔ; quarum AB ad ΛΦ eadem quae LG ad GK et ΛΦ ad ZΔ eadem quae KH ad HS. Itaque apparet, posito oculo in Q, visibili vero in M, rationem incrementi esse eam quae ex rationibus LG ad GK et KH ad HS componitur. Quamobrem et oculo ad M collocato visibili vero ad Q, uti est PR, eadem quoque erit incrementi ratio {* Prop. II.
Ratio autem AB ad XY sive ad ZΔ, componitur ex rationibus AB ad ΛΦ et ΛΦ ad ZΔ; quarum AB ad ΛΦ eadem quae LG ad GK et ΛΦ ad ZΔ eadem quae KH ad HS. Itaque apparet, posito oculo in Q, visibili vero in M, rationem incrementi esse eam quae ex rationibus LG ad GK et KH ad HS componitur. Quamobrem et oculo ad M collocato visibili vero ad Q, uti est PR, eadem quoque erit incrementi ratio {* Prop. II. Accipiatur lens major AB, cujus foci distantia sit AC. Deinde vero aliae duae minores DT et QR, quarum foci distantiae EL, HF sint inter se aequales et ad quarum utramvis habeat AC rationem eam secundum quam facienda est multiplicatio. Collocentur autem hoc pacto ut distantia CE, qua altera earum abest a foco lentis A, sit dupla EL: Et EH intervallum inter utramque ejusdem EL triplum. Denique ad K punctum constituatur oculus, sumtâ HK distantia dictae EL vel FH dupla vel paulo amplius. Quibus sic comparatis propositum dico absolvi.
Accipiatur lens major AB, cujus foci distantia sit AC. Deinde vero aliae duae minores DT et QR, quarum foci distantiae EL, HF sint inter se aequales et ad quarum utramvis habeat AC rationem eam secundum quam facienda est multiplicatio. Collocentur autem hoc pacto ut distantia CE, qua altera earum abest a foco lentis A, sit dupla EL: Et EH intervallum inter utramque ejusdem EL triplum. Denique ad K punctum constituatur oculus, sumtâ HK distantia dictae EL vel FH dupla vel paulo amplius. Quibus sic comparatis propositum dico absolvi. [Hoc*) aliter demonstrari potest, ut non opus sit theoremate de transpositione oculi et objecti. Scilicet HKR ad SΛX sive AΛΔ rationem habet compositam ex HKR ad HOR, id est, ex HO ad HK, et ex HOR sive EOD ad AΛΔ, id est, ex AΛ sive AC ad EO sive EL; quia vero HO aequalis HK, erit HKR ad SΛX ita AC ad EL. q.e.d.]
[Hoc*) aliter demonstrari potest, ut non opus sit theoremate de transpositione oculi et objecti. Scilicet HKR ad SΛX sive AΛΔ rationem habet compositam ex HKR ad HOR, id est, ex HO ad HK, et ex HOR sive EOD ad AΛΔ, id est, ex AΛ sive AC ad EO sive EL; quia vero HO aequalis HK, erit HKR ad SΛX ita AC ad EL. q.e.d.]
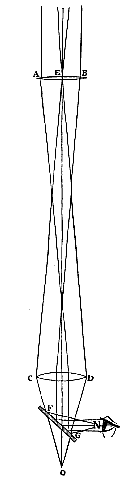 Sed interdiu ad conspiciendos homines turresve aut naves procul dissitas, situs eversio res agnosci non patitur, atque ideo plures convexae lentes adhiberi solent, ut imaginem quam duae invertunt aliae denuo erigant, de quibus propos. praecedenti egimus. Quia vero hoc fieri nequit quin simul insigniter augeatur tubi longitudo atque amittatur multum de picturae amplitudine; excogitavimus rationem hanc qua eversae species in telescopio duorum convexorum erigantur adjecto ad oculum speculo exiguo, cujus positum locumque sequenti schemate explicabimus.
Sed interdiu ad conspiciendos homines turresve aut naves procul dissitas, situs eversio res agnosci non patitur, atque ideo plures convexae lentes adhiberi solent, ut imaginem quam duae invertunt aliae denuo erigant, de quibus propos. praecedenti egimus. Quia vero hoc fieri nequit quin simul insigniter augeatur tubi longitudo atque amittatur multum de picturae amplitudine; excogitavimus rationem hanc qua eversae species in telescopio duorum convexorum erigantur adjecto ad oculum speculo exiguo, cujus positum locumque sequenti schemate explicabimus.