Dioptrica

De Telescopijs [ Ca. 1685 ] Praefatio   Primum ac praecipuum eorum quae in hac refractionum doctrina tractantur Telescopiorum est ratio; magni inprimis inventi, cujus praestantiam pro dignitate nemo satis depraedicaverit. Ut enim caeteras utilitates praeteream de quibus postea dicetur*), quantum hoc est, in caelestium contemplatione ad ea viam aperuisse, quae nulla alia ratione investigari poterant. Unde et rerum naturae mirabilia multa patuerunt, et totius denique mundi constitutio, ut qua regione tellus haec nostra, nosque qui eam incolimus positi simus, multo quam ante certius compertum comprobatumque sit. Qua cognitione nihil mihi majus meliusve hominum solertia perfectum esse videtur. Quod si quis tanta industria extitisset ut ex Naturae principijs et Geometriae hanc rem eruere potuisset, eum ego supra mortalium sortem ingenio valuisse dicendum crederem. Sed hoc tam longe abest, ut fortuito reperti artificij rationem non adhuc satis explicare potuerint viri doctissimi.   *)  On n'en trouve rien dans la "Dioptrique".

[ 437 ]

[ v ]

Sunt qui inventionis, sed uti dixi fortuitae, primae laudem Jacobo Metio Batavo Alcmariae civi tribuant. Mihi vero certo compertum est [>] ante ipsum telescopia fabricasse artificem quendam Medioburgensem apud Zelandos circa annum hujus saeculi 9. sive is fuerit cujus Sirturus meminit Joh. Lippersheim nomine, sive cui Borellus in libello de vero Telescopij repertore primas defert Zacharias*). Hi tunc non majores sesquipedalibus tubos factitabant. Utroque vero multo prior rudimenta artis suggesserat Joh. Bapt. Porta Neapolitanus, cujus exstant de rebus dioptricis, et Magia Naturali, libri totis 15 annis ante editi quam in Belgio nostro telescopia exorirentur. In quibus libris de specillis (ut vocat) suis memorat res procul positas quasi propinquae essent referentibus, deque conjunctione cavarum et convexarum lentium°). Nihil tamen magnopere eum profecisse, hoc ipsum probat quod tanto tempore ars jam coepta non ultra inclaruit, neque ipse Porta quidquam in caelo observavit eorum quae postea apparuerunt. Hoc inde est quod fortuitis experimentis originem inventi deberi constat. Neque enim hic vir licet mathematicarum aliquatenus gnarus subtilissimas rationes quibus ars ea pro fundamentis utitur comprehenderat, ut meditatione eam eruere posset, multoque minus illi quos ante memoravi homines opifices ac scientiarum rudes. Fortuna vero et casu eodem perventum nihil mirum est, cum frequens usus esset jam a trecentis atque amplius annis utriusque generis lentium quibus seorsim adhibitis vitia oculorum emendantur. ut potius mirandum sit tam diu rem obviam latuisse.   [ *)  Zacharias Jansen. Sirturus, Telescopium, p. 24 (Frankfurt 1618); Borellus, de Vero telescopii inventore (Den Haag 1655/6).]   °)  Giambattista della Porta, Magiae naturalis libri viginti, 1591; p. 597: 'De specillis', p. 595: Lentes [Engl. 1658, Ch. 10, 11]. [ De refractione optices, 1593 — Cat.'95, Math.4to.65.]

[ 439 ]

[ v ]

Caeterum ut primum Telescopium Belgicorum fama sparsa erat continuo Galilaeus similia illis, ac brevi multo praestantiora paravit, quibus celeberrima illa caeli phaenomena omnium primus deprehendit: Lunae montes vallesque, Solis maculas, et ex his conversionem ejus in semet ipsum, Planetas Jovis comites, Phases Veneris quales Lunae, variasque ad aspectum magnitudines; Viam lacteam minutis stellulis refertam, unde candoris causa. Differentiam stellarum inerrantium inter et planetarum diametros, atque illarum numerum antiquitus cognito multo majorem.

Marge:

in luna non esse maria nec fluvios nec nubes

Idem Galilaeus Saturni quoque phaenomena observaverat, qua licebat in illa perspicillorum suorum parvitate, veras autem planetae figuras adsecutus non erat, sed neque quisquam alius multis post ipsum annis. Etsi enim magnitudine multum creverant tubi, parum tamen virtute et efficacia processerant. Nos autem magis auspicato rem eandem aggressi, cum quae ad refractiones radiorum attinent studiose investigassemus, ipsique nobis lentes effecissemus ac telescopia pedes viginti et amplius longa, his Saturni formas non ante visas deprehendimus causamque earum annulum globo circundatum, nullo in caeteris planetis exemplo. item comitem Saturno planetam exiguum reperimus dierum sexdecim periodo circumeuntem, quae omnia ante annos 26 libro singulari conscripta edidimus*). Nostris autem observationibus excitati astronomi atque artifices majora subinde telescopia paraverunt, in quibus optima quae a Josepho Campano Romae fabricata. Quorum opera feliciter usus decennio post duos alios praeter nostrum illum comites apud Saturnum reperit dom. Cassinus. Idemque in Jovis ac Martis sideribus maculas quasdam observavit, ex quarum motu etiam globorum quibus inerant conversiones statis temporibus definitas.   Et hactenus quidem adhuc processit nobile hoc artificium, haecque summa est eorum quae de rebus caelestibus terrarum incolis revelavit. Quae magna ac praeclara esse quis nisi plane stupidus non agnoscit? Quanta vero ad naturae contemplationem lux hinc exorta sit, quis non philosophiae studijs initiatus intelligit? Certe gratari saeculo huic nostro possumus propter tantarum rerum nunc demum acquisitam scientiam: quam quo non pretio redemissent viri illi eximij, non longo annorum intervallo hinc exclusi Copernicus, Regiomontanus, Braheus.   *)  Systema Saturnium (1659).

[ 441 ]

[ v ]

Veteres autem illi sapientiae cultores Pythagoras, Democritus, Anaxagoras, Philolaus, Plato, Hipparchus quas non exteras terras peregrinando pervagati essent hujusmodi naturae secretorum noscendi amore, utque talibus frui possent spectaculis. Fortasse autem et alia plura ac nova praeter ea quae diximus propediem expectanda sint, postquam nupero invento nostro*) ingens incommodum ex nimia tuborum mole ac pondere ortum, atque adeo ipsos tubos, sustulimus, ut nihilo difficilius nunc centenum vel ducentorum pedum telescopia quam antea decempedalia tractentur. utique cum et expoliendarum amplissimarum lentium artem plures jam excolere coeperint, cujus nos quoque studium longo tempore intermissum repetijmus, nec poenitendo successu°). Sed jam ad caussas proprietatesque factitij hujus oculi pergamus, quas non satis feliciter hactenus expositas habemus.   Quod enim hic prae caeteris requirebatur ut data lentium forma ac positu ex his modus mensuraque amplificandae rei visae definiretur, id hactenus praestitum non est. Nam neque Keplerus hoc docuit, etsi multa laude dignus ob ea quae in dioptricis primus explicuit, neque illo felicior fuit Cartesius, imo ut vere dicam a via potius aberravit in his quae de ratione et effectu telescopij demonstranda susceperat [<]. Quod vix credibile de tanto viro, tamque in his rebus versato, tamen dicendum fuit, ne quis frustra ea intelligere laboret e quibus nulla apta sententia elici potest. Cum vero alij multi post eum in eodem argumento operam insumserint, nihilo magis tamen idem problema quod in his omnium praecipuum est absolverunt. Ab eo nunc nos ordiemur idque in singulis telescopiorum generibus expediemus.   Ostendimus autem in superioribus [<] in universum data forma et positu duarum quarumlibet lentium, itemque oculi loco, quomodo augmenti ratio cognoscatur. At quia nunc illos tantum casus quos telescopia requirunt exequi necesse est, brevius idem conficiemus. Ac primum quidem in illo telescopiorum genere quod e convexa et cava lente componitur omniumque primum fuit inventum.   *)  Astroscopia (1684).       °)  Memorien (1685).

[ 443 ]

[ v ]

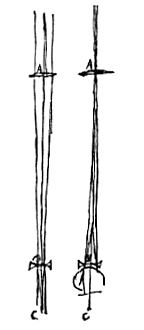
Requirunt vero primo eam lentium positionem telescopia omnia, ut distincta visio sequatur. ut vero auctiora referant quae spectantur, necesse est in his quae duabus lentibus constituuntur ut exterior convexa sit, ejus vero quae est oculo propiore minori sphaera sit sive convexitas sive cavitas.   Sit lens exterior convexa A, ocularis cava B, oculus D; lentis A focus sit C, idemque punctum dispersus lentis B, radiorum nempe parallelorum inde ubi est oculus advenientium, quo fit vicissim ut qui refractione lentis A tendunt ad C punctum, denuo paralleli fiant postquam lentem B transierint, unde distincta visio consequitur. Haec vero radiorum flexio priore figura exhibetur, in qua radij paralleli, in A lentem incidentes, ex uno quopiam rei visae ac longissime distantis puncto manare intelligi debent (habentur enim pro parallelis ob ingentem distantiam licet revera non sint); qui refracti tendunt ad punctum C, et a lente B intercepti rursus paralleli efficiuntur. Similiter vero a singulis rei visae punctis aliae atque aliae series radiorum inter se, non autem his quas diximus, parallelorum in lentem A deferri intelligendae, qui paralleli ad totidem puncta juxta C posita, colligantur, atque itidem refractione cavae lentis B ad parallelismum redigantur, itaque oculo occurrant.*)   *)  [...] Une autre leçon, de date postérieure, du début de la Prop. I qui suit. Il est possible que cette Prop. et les deux qui suivent aient été rédigées entièrement, ou en partie, bien avant 1685, mais toujours après 1666; [...]. Propositio I   Telescopium ex convexa et cava lente compositum visibilia longinqua, distincte ac recto situ videri facit, amplificatque secundum rationem foci distantiae lentis convexae ad distantiam puncti dispersus lentis cavae.   Sit utriusque lentis axis communis AO; lens vero exterior convexa A, cujus punctum concursus radiorum parallelorum, a visibili longe remoto venientium, ponatur O punctum. Cava autem sit D, quae sic collocetur inter lentem A et focum ejus O, ut punctum dispersus radiorum parallelorum a parte ea ubi est O in ipsam incidentium, cadat in idem punctum O. Et huic lenti proximus primo statuatur spectantis oculus.   Radij igitur a puncto rei longinquae egressi censentur paralleli incidere in lentem A, ij quidem qui ex puncto in axe producto procedunt cogerentur ad punctum O; sed rursus paralleli evadent opera lentis D, ita ut dictum est collocatae, uti ex supra demonstratis constat. Parallelos enim radios ad oculum pervenire volumus, ut bona oculi constitutione fruentibus telescopium aptetur; nam de myope dicemus postea.

[ 445 ]

Similiter vero a punctis longinquis extra axem positis manantes colligerentur quique ad puncta sua prope O, sed et hi lentis D refractione evadent denuo paralleli quamvis ad axem AD obliqui, secundum prop. [I.XXII] quos radios tamen in figura non expressimus, vitandae confusionis gratia.   Jam ex demonstratis prop. [II.I] patet eandem fore amplificationem et positum, manente lente utraque, atque cum loco lentis D foramen exiguum statuetur; tunc vero magnitudinis apparentis ad veram ea est ratio quae AO ad OD, ut ostensum prop. [II.II], et ex eadem visibile erectum spectatur. Ergo eadem hîc fiunt telescopio ex lentibus A, D composito. Quod si vero retrocedat oculus ab lente D, eadem remanet rei visae magnitudo apparens ex prop. [II.XIII]. nec vera mutatur, quia visibile longinquum ponitur. Ergo eadem quae prius manet amplificatio. Sed et positus idem ex eadem prop. [XIII].   Quod si myopi aptandum sit hujusmodi telescopium, paulo propius admovendam esse constat lenti A lentem ocularem D unaque oculum spectatoris; quoniam sic fiet ut non jam paralleli ut antea radij perveniant ad oculum, sed divergentes. Hinc vero paulo minus augmentum continget myopi quam prius cum punctum O maneat, eoque intervallum DO crescat, ratio vero augmenti sit semper ea quae AO ad OD.   Et haec quidem primarij theorematis brevissima est demonstratio. Cujus partem eam quae ad amplificationem rei visae attinet aliter quoque demonstrabimus, ut nihil opus sit prop. [II.V].

[ 447 ]

[ v ]

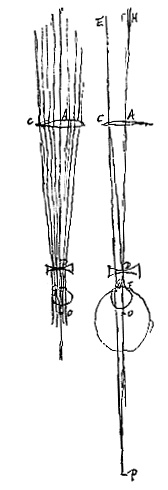Positis igitur ut ante lentibus AC et D et puncto O, fiat duabus DO, DA, tertia proportionalis DP, ponenda in eandem partem ac DO. Jam radij quilibet ad punctum P tendentes ut ECP et a lente AC refracti, cogentur ad punctum D lentis hic positae centrum ex prop. (XX, Lib. I)*). Ponamus istum ECP radium esse unum ex ijs qui a dextro [sinistro] lunae latere egrediuntur, cum centrum Lunae sit in producto axe DA. Et constat quidem hunc recta linea CDF ad oculi pupillam perventurum, quia per centrum lentis D transit, cujus mediae crassitudo pro nulla habetur, et duae ejus superficies ibidem pro parallelis. Diximus autem omnes a puncto illo lunae procedentes inter se parallelos ad oculum deferri. Itaque sic omnes recipit oculus ut radio CDF paralleli incedant; ac propterea punctum illud in lunae latere videt eo loco quo tendit recta DC, quae cum in eandem partem axis tendat ad quam situm est punctum lunae unde radij advenere, apparet erectas exhiberi res visas. Porro angulus ADC definit semidiametrum lunae telescopio auctae. Sed angulus CPA est is quo nudo oculo iste semidiameter comprehenditur, quia radium ECP a dextro lunae latere exire diximus, radium vero HAP, a centro ejus, nam sive e puncto P, sive ex G luna spectetur nudo oculo eodem angulo apparet propter maximam distantiam. Itaque amplificatio contingit secundum rationem anguli ADC ad APC, quae censetur hic eadem ac rectae PA ad DA; sed quia ex constructione est DO ad DA ut DA ad DP, erit invertendo et componendo AO ad OD ut PA ad AD. Ergo jam amplificationis ratio est quae AO ad OD; quod erat demonstrandum.   Apparet autem hic nihil referre quantum ad amplificationem quo loco post lentem oculus constituatur.   *)  D'après cette proposition P est le point auquel correspondent les rayons réfractés partant du point D. Donc en invertissant le sens dans lequel ces rayons sont parcourus on trouve que les rayons qui se dirigeaient vers P se réuniront en D après leur réfraction par la lentille. [ Avec: DO = f – v, DA = v, AP = –b, DP = –b – v,   on aura: (f – v) / v = v / (–b – v),   correspondant à: 1 / f = 1 / v + 1 / b .]

[ 449 ]

[ v ]

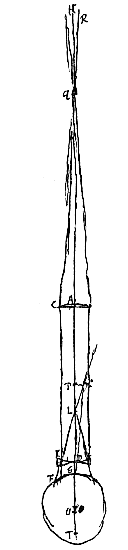Ponantur rursus lentes AC et D ut ante, et sit AQ in axe earum producto aequalis AO. Accipiamus jam ex radijs ijs qui a puncto lateris dextri lunae adveniunt radium RQC qui per Q punctum transiens (aliquis enim eo transibit) occurrat lenti AC in C. Is hinc parallelus fiet axi AD, et refractione altera lentis cavae D diverget ac si veniret a puncto L, et ad oculum feretur secundum rectam LIF, ut nempe distantia LD sit aequalis DO, quia tunc L est punctum dispersus parallelorum in lentem D incidentium. 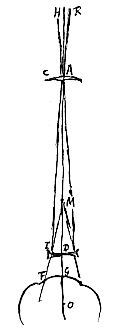  Proportio autem auctae magnitudinis facile jam hic colligitur. Quia enim radij a puncto in latere lunae dextro egressi perveniunt paralleli ad pupillam GF, postquam utramque lentem pervasere, omnesque propterea paralleli fiunt radio LIF, quem constat esse eorum unum; percipietur illud lunae punctum secundum rectam IL, ac proinde angulo ILD semidiameter lunae comprehendetur. At vero angulus quo semidiameter spectabitur oculo nudo sive ex D sive ex Q, est RQH, sive CQA. Ergo ratio augmenti est ea quae anguli DLI ad AQC, hoc est, quae rectae AQ ad LD, propter aequales AC, DI. Sed AQ est aequalis AO, et LD aequalis DO. Est ergo ratio augmenti ea quae AO ad OD; quod erat ostend.   Potest idem rursus demonstrari ex intersectione radiorum quae in A centro lentis AC contingit. Sequendo nimirum radium RA unum in hac figura eorum qui ex lunae dextro latere adveniunt, qui recto cursu lentem hanc penetrabit, cum pro nulla habeatur ejus crassitudo, per prop. (XXIII, Lib. I). Deinde occurrens lenti cavae in I ita ejus refractione diverget, ac si a puncto M exiret, quod invenitur ponendo duabus AO, AD tertiam prop. AM ut constat ex prop. (XX, Lib. I). Itaque rursus hic radij qui a puncto in latere dextro lunae adveniunt, quoniam, post utriusque lentis refractionem, paralleli ad oculum feruntur, ut supra fuit animadversum, debebunt omnes ipsi MIF paralleli ferri, eoque punctum illud conspici secundum rectam FIM. Unde jam intelligitur rationem amplificationis fore eam, quae anguli DMI ad DAI seu HAR. Est autem ang. DMI ad DAI reciproce ut AD ad DM, hoc est ut AO ad OD, quia proportionales factae AO, AD, AM. Itaque rursus constat propositum.

[ 451 ]

[ v ]

Hac via causas telescopij melius investigasset Cartesius, [quam] ex intersectione radiorum quae sit in superficie lentis exterioris, qua intersectione ille utendum putabat [<]; quod tamen haudquaquam necesse esse ex ijs quae hic ostensa sunt satis liquet. At nunc multiplici errore implicita est ejus expositio quae in dioptricis legitur, uti et schema ipsum, neque ex ijs unquam proportionem amplificationis colligere potuit. Cujus ignoratione majorem quoque multo quam rei natura patitur de telescopij efficacia spem concepit. Putabat enim si artificum industria praestare posset quod ars docet, fore ut res tam particulares et minutas in astris videremus, quam sunt eae quas vulgo in terra percipimus*). Cum tamen non nesciverit eadem proportione qua res visae amplificantur, etiam diametrum lentis exterioris superare debere pupillae latitudinem, ut lucida omnia telescopio aeque ac nudo oculo spectentur. Nam, licet jam quarta parte hujus claritatis contenti simus, invenio tamen aperturam illam lentis exteriorem Terrae diametro majorem esse debere, si res in Jove tanquam 40 pedibus distantes spectandas praebere postulet. Ut appareat aliud quam manuum industriam hic requiri.   *)  [ Cf. Isaac Beeckman, Journal III, 114 (1629), et une remarque dans une lettre de Chapelain (24 août 1656), cf. I, 483.]   Voici le passage où Huygens a fait ce calcul, lequel suivait les mots "in terra percipimus", mais qui fut rayé plus tard:   Sed aliud quam manuum industriam hic requiri calculo facile evincitur. Putemus enim telescopium parandum quo res in Jovis Planeta tanquam 10 pedibus distantes discerni queunt. Jupiter in oppositu solis situs quadruplo plus a terra quam haec a Sole distat. Terrae a Sole distantia est secundum nostrum et Peritiorum nostrae aetatis Astronomorum calculum, circiter 12000 Terrae diametrorum. Ergo a Jove acronychio 48000 talium diametrorum; diameter terrae amplius quam 40000000 pedum nostratium. Absumus ergo a Jove pedibus 1,920,000,000,000. Oportet autem telescopium nos deducat ad 10 pedum distantiam. Ergo res visae diametrum augere debet secundum rationem 192,000,000,000 ad 1. Quod ut fiat, debebit diameter lentis exterioris esse ad latitudinem pupillae in hac eadem ratione si postuletur aeque lucidas res conspici telescopio ac nudo oculo. Sed putemus quartam partem ejus claritatis sufficere. Continebit ergo diameter lentis diametrum pupillae toties quot sunt unitates in numero 48,000,000,000. Pupillae vero diameter saltem 1/144 pedis partem efficit. Ergo facta divisione per 144, fit numerus pedum quos haberet latitudo lentis 333,333,333, quae major est quatuor Terrae diametris. Propositio II   Quaenam sit amplitudo anguli visorij seu spatij quod uno intuitu exhibet telescopium ex convexa et cava lente constructum.

[ 453 ]

[ v ]

A pupillae magnitudine praecipue pendet amplitudo anguli visorij in hisce telescopijs, idque experiri licet, nam si oculum telescopio admotum claudas primum, quo pupilla multum dilatetur ut in tenebris solet, deinde aperias, primo intuitu latiori orbe visibilia comprehendes quam paulo post, quia statim contrahetur orbis ob arctatam fulgore lucis pupillam. Quod si lamellam cum exiguo foramine oculo opponas, minori etiam copia rerum visibilium frueris.   Veruntamen si minimum foramen efficias non pro ratione ejus exilitatis orbis lucidus arctabitur, sed tunc apertura lentis convexae amplitudinem ejus definit, quae proinde non ultra certam quantitatem decrescet nisi et lens convexa amplius coarctetur. Quorum ratio explicatu facilis est. Si enim lens convexa sit EF, cava B, cui applicata pupilla primo latitudinem habeat CD, ducanturque ab oppositis punctis C, D, quae sunt in pupillae circumferentia, rectae CAH, DAG, per centrum lentis convexae A transeuntes; hae definient angulum visorium GAH, quo, quicquid rerum visibilium comprehenditur, uno obtutu conspicietur, quoniam per centrum lentis A radij a punctis G, H venientes absque inflexione penetrant ad C et D; ideoque aspectabilia intra angulum GAH comprehensa non possunt quin ad oculum radios emittant. Imo etiamsi pupilla pauxillo angustior sit quam DBC, nam ducta GAK ut AK sit aequalis AO, junctaque EK: dummodo EK in pupillam incidat, cernetur visibile comprehensum angulo GAH. obscure vero puncta extrema quo tendunt rectae AG, AH, quia particula tantum radiorum quos in lentem EF mittunt, pupillam ingreditur. Atque hinc fit ut quantumvis in angustum apertura lentis EF contrahatur, nihil aut minimum tantum diminuatur anguli visorij amplitudo, dummodo pupillae orbis non coarctetur. Diminuta autem hac pupillae latitudine, atque ad unum velut punctum redacta, anguli visorij amplitudo fit ea quae anguli EPF, posita EF apertura lentis convexae, et puncto P invento, ut in prop. [II.II], ut nempe BO, (ea est distantia lentis cavae a foco convexae) BA, et BP sint proportionales. Nulli enim radij, per lentem A transmissi, ad punctum oculi B pervenire possunt, nisi qui priusquam in lentem illam inciderent tendebant ad punctum P. Eorum vero maximus angulus EPF apertura lentis A praefinitur.

[ 455 ]

[ v ]

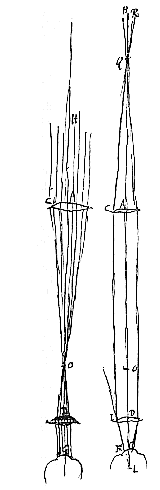Propositio III   Telescopium e duabus convexis lentibus compositum procul posita distincte sed eversa ostendit, amplificatque secundum rationem foci distantiae lentis exterioris ad foci distantiam interioris.   Sit lens exterior convexa AC, interior D, axis communis utrique recta AD. Focus lentis AC sit O. Altera vero convexa D ita collocata intelligatur ut idem punctum O sit ipsi focus seu punctum concursus radiorum axi AD parallelorum qui venirent a parte ea ubi est oculus G. Ostendendum est his positis res longe dissitas distincte et eversas spectari et augeri secundum rationem AO ad OD.   Duplex autem rursus describenda est figura, in quarum altera radij extrinsecus venientes, axi HA paralleli, refractione lentis AC cogantur ad focum ejus O, atque inde ulterius tendentes ad lentem D, denuo paralleli fiant axi AD, atque ita ad oculum in G positum perveniant. Rursus etiam sicut superiori propositione cogitandum hunc parallelorum complexum ab uno rei procul dissitae puncto venire, quod sit in axe HAD, velut a centro Lunae, ab alijs vero punctis ejus similes manare radiationes parallelas in lentem AC velut e latere Lunae dextro, qui ad priores inclinentur, et hinc refracti cogantur ad punctum extra axem juxta O, ubi sese interecantes, atque ad lentem D delati denuo paralleli evadant, inter se nempe non autem axi AD, atque ita ad oculum perveniant. Hinc itaque constat visionem distinctam fieri.   Altera porro figura, situm visibilis eversum, et rationem augmenti ostendet. Ubi positis ut ante, lentibus convexis AC et D, et inter ipsas foco utriusque communi O; sit porro, ut in secunda demonstr.e Telescopij superioris [<], distantia AQ aequalis AO. Et reliqua quoque demonstratio fere eodem modo procedet. Seligatur enim ex radijs qui e puncto in latere lunae dextro adveniunt radius RQC qui per punctum Q transit.

[ 457 ]

Is refractione lentis AC ibit per CI parallelam AD, et rursus a lente D refractus tendet secundum rectam IFL ad punctum L, ita sumtum ut distantia DL sit aequalis DO. Quia autem radij a latere lunae dextro, postquam per utramque lentem transierunt, paralleli perveniunt ad oculum, ut antea diximus, eorum vero unus est IFL, sequitur eos omnes ipsi IFL parallelos in oculum incidere, eoque illud lunae punctum percipietur secundum rectam FI; quae cum ad partem oppositam vergat ejus unde hi radij advenere apparet situm lunae inverti, ut dextra sinistris, eoque et supera inferis mutentur. Porro cum centrum Lunae secundum rectam DA conspiciatur, erit apparens angulus semidiametri lunae ILD. Nudo autem oculo idem semidiameter angulo HQR seu AQC comprehenditur. Ergo ratio amplificationis est quae anguli AQC ad DLI, hoc est quae AQ ad DL, propter aequales AC, DI, hoc est, ea quae AO ad OD; quare constat propositum.   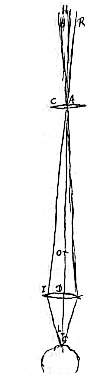Hic vero nihil quoque referre apparet quantum ad apparentem magnitudinem quo loco post lentem D oculus collocetur [<]. Sed ut multa uno intuitu oculus comprehendat ad punctum L vel prope ipsum optime constituetur, quoniam apparet, etiamsi minima sit pupillae latitudo, totam tamen lentem D quatenus aperturam lentis AC non excedit (solet autem intra hanc mensuram consistere), imaginibus plenam spectari.   Ostendemus autem sequenti demonstratione dari punctum paulo ultra L a lente D distans, ubi si collocetur oculus totam lentem D pictura lucentem aspiciet, etiamsi minimae fuerint tum pupillae tum lentis AC apertura.   Dispositis enim sicut ante lentibus AC, D, ut focus earum communis sit punctum O. Statuatur duabus AO, AD tertia proportionalis AG, unde punctum G ultra L distabit a lente D, cum DL, DO sint aequales. Erit autem ad G ponendus oculus, ut fiat quod dictum est.   Si enim, ut in tertia demonstratione telescopij ex convexa et cava compositi [<], sequamur rursus radium RA unum eorum qui ex puncto in dextro rei visae latere adveniunt quique incidit in centrum lentis AC, is recta linea hanc penetrabit secundum prop. (I.XXIII) cum pro nulla habeatur ejus crassitudo.

Marge:

Poterat et radius seligi qui per centrum ocularis ut in prima demonstr. telescopij prioris [<].

Deinde lenti D occurrens in I, cogetur hujus refractione ad punctum G, quod est pupillae medium, propterea quod proportionales sunt AO, AD, AG. Itaque quicquid angulo DAI sive HAR oculo nudo comprehenditur spectabitur in lente D; adeo ut campi (ut vocant) amplitudo jam pendeat a latitudine lentis D, licet aperturae lentis A et pupillae sint veluti puncta. atque ita quoque omnino si utraque magis pateat.

[ 459 ]

[ v ]

Sciendum vero neque lentem D nimis amplam esse adhibendam, propter incommodum colorum ex nimia refractione, de quo in sequentibus dicetur [>]; nec nimis arctandam aperturam lentis AC, ne obscuritas inducatur. certa autem mensura ejus alibi docebitur. Pupilla vero licet apposita lamellae cum foramine, quantum acus facere potest, in angustum contrahatur, nihil fere lucis aufert, quoniam coni radiosi a singulis rei visae punctis manantes insigni tenuitate sunt cum incidunt in lentem D, quam retinentes inde paralleli ad oculum pergunt.   Porro facile rursus hic intelligitur proportionem ampliationis esse eam quae anguli DGI ad HAR sive DAI, hoc est eam quae AD ad DG, sive quae AO ad OD, quia DA ad AO ut GA ad AD.   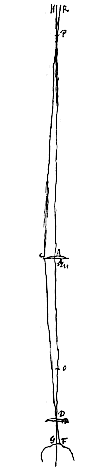Atque haec proportio aliter rursus, ut in demonstratione prima ex cavo et convexo [<] comprobari potest, sequendo radium illum qui a puncto rei visae extra axem telescopij posito manans deducitur lentis AC refractione ad centrum lentis ocularis D. Hoc enim patet ex inspecta figura hic adscripta, in qua eadem est constructio ac demonstratio quae fuit illic.   Hinc porro apparet quanto praestent Telescopia ex convexis duobus composita ijs quorum lens ocularis cava est, cum tanto amplius spatium uno intuitu comprehendant. Est enim angustia illa spectaculi injucunda et prorsus incommoda praesertim si ultra tres quatuorve pedes tubi extendantur. Quare etsi Galilei egregium illud perspicillum ac tot novis repertis celebre ex convexo et cavo fuerit conjunctum, nunc tamen ejus generis nulla nec ad syderum observationes nec ad res in Terra spectandas adhibentur, sed tantum e convexis composita. Unicus vero usus cavoconvexorum in minima longitudine relictus est, 4 nempe aut 5 digitorum, in qua brevitate tolerabilis jam latitudo anguli istius visorij reperitur. In hujusmodi perspicillis ratio incrementi facienda est quadrupla circiter. Sed et dupla non majorem utiliter adhibere solemus. quo fit ut lucida etiam intra aedes omnia spectentur. Et stellae melius quam oculo nudo, multaeque simul, quoniam in tali perspicillo apertura exterioris lentis vel ad sesquipollicem patere potest.

[ 461 ]

[ v ]

Ac possunt quidem binae convexae lentes parari tales, atque ita inter se componi, ut erecta referant visibilia longinqua; nec tamen quicquam boni inde obtinebitur, quod nec paralleli ad oculum tunc radij pervenire possunt qui e singulis rei visae punctis emanant, neque eae multum amplificari, nec magna copia simul conspici, praeterquam quod tubi longitudo sine utilitate multum producenda esset.   Tribus vero lentibus convexis et recto positu et distincta possunt videri [<], sed non tam lato campo quam quaternis, nisi lens oculo propior duplam fere aperturae diameter habeat ejus quae in similibus ocularibus requiritur, cum tria adhibentur, quod fieri nequit quin colores iridis circa margines existant. Propositio IV   Quomodo pro duobus convexis tria adhibendo amplior fiat telescopij prospectus, quo ad sidera spectanda utimur.

[ 463 ]

[ v ]

Quanquam lentes non frustra sint multiplicandae, quod et vitri crassitudine et iteratis reflexionibus non parum lucis depereat; hanc tamen utilitatem praebere potest, ut latior evadat eoque jucundior telescopij prospectus. Adsumtis enim praeter magna lentem ocularibus duobus certam inter se rationem distantiamque habentibus, tunc multo minor fit aberratio radiorum a diversis punctis rei visae ad oculum tendentium, quam si unica lens ocularis adhibeatur, quae eandem amplificationem efficiat, atque ita multo plura longe unico intuitu comprehendere licet, ac praeterea naevi ac impuritas omnis lentium ocularium plane evanescit, cum alioqui in una lente non parum adferat incommodi.     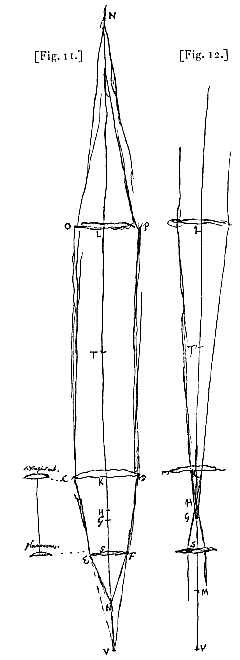Sit ratio augmenti proposita ea quae P ad Q. Lens exterior L [Fig. 11 et 12]. focus ejus G. Et ut P ad Q ita sit LG ad GK, cadente puncto K inter L et G. Et in K lens convexa statuatur cujus foci distantia KV sit tripla ad KG, et divisa KV aequaliter in S, statuatur ibi lens altera EF cujus foci distantia SH sit 1/2 SK. Oculus vero sit in M, posita SM distantia 1/2 KG. Erit factum quod quaeritur.   Demonstrationem vero duplici figura explicamus. In quarum priori [Fig. 12] expendimus radios ab uno aliquo rei visae puncto manantes, quod punctum in axe telescopij positum intelligi volumus. Qui itaque radij velut axi paralleli in lentem L incidere censentur. Unde porro tendere debent ad hujus lentis focum G. Sed refractione, quae fit in lente K, ostendemus eos mitti ad punctum H; atque inde sese intersecantes atque in lentem S incidentes, reddi parallelos, itaque ad oculi pupillam M pergere. Posita enim KT aequali KV, quae erat foci distantia lentis K, quia KG dicta est esse 1/3 KV; KH vero 1/4 KV. Erit GH ad GK ut 1 ad 4; sed et GK ad GT erit ut 1 ad 4. Ergo proportionales GH, GK, GT. ac proinde radij ad G tendentes flectentur refractione lentis K ad H, cum sit H focus lentis S, faciet haec ut a puncto H pergentes paralleli fiant, qui proinde oculo ad M occurrentes distinctam visionem efficient, quod unum est eorum quae demonstrare oportebat.

Marge:

GT (a + x) ad GK (x) ut GK (x) ad GH (xx/(a + x))   1/4 a + xx/(a + x) x   luna tota simul ang.o 60 gr. jucundum spectaculum.

[ 465 ]

[ v ]

Jam in altera figura [Fig. 11] ratio amplificationis eadem datae ostendetur et amplitudo anguli visorii. Ponatur enim LN in producto axe aequalis foci distantiae LG. Et a punctis longinquis venientes radij expendantur per punctum N transeuntes atque in lentem L extremam utrimque incidentes, qui sint NO, NP. quos constat refractione ejus effici axi parallelos, atque ita incedant per OC, PD, donec incidant in lentem K. Unde porro scimus pervecturos rectis CV, DV ad punctum V. Sed a lente S interceptos ajo detorqueri ad punctum M, ubi oculi pupilla posita fuit. Quia enim SV est 1/2 KV; et SM 1/2 KG, hoc est 1/6 KV; erit SM ad SV ut 1 ad 3, ac proinde VM ad VS ut 2 ad 3. Sed et VS ad VH est ut 2 ad 3. Ergo proportionales VM, VS, VH et quia H est focus lentis S, constat ex propos. (I.XX) radios ad V tendentes ita frangi a lente S ut tendant ad punctum M.

[ 467 ]

[ v ]

A punctis igitur E et F, in quibus rectae CV, DV secant lentem S, ducantur rectae EM, FM. Sic 1) visibile per lentes cernetur sub ang. EMF qui ad ONP habet proportionem, ut LG ad KG, id est, ut P ad Q. Quia enim ratio EMF ad ONP, id est, EMS ad ONL componitur ex rationibus EMS ad EVS, et EVS ad ONL; ratio vero EMS ad EVS eadem est, quae VS ad MS sive 1/2 KG, item ratio EVS ad ONL eadem quae NL sive LG ad KV sive 2 VS. Erit ratio EMF ad ONP composita ex 2 VS ad KG, et LG ad 2 VS, id est, erit EMF ad ONP ita LG ad KG, ita P ad Q: quod erat dem.   Videndum 2) an quid juvet. Et an non idem effectus sit, ac si ponatur sola ocularis α [Fig. 13], cujus foci distantia Gα KG [Fig. 11] hoc est 1/3 a 3); quum angulus αMβ sit futurus aequalis KGD, hoc est, SMF; nam KD 2 SF 4), et KG 2 SM 5). Resp[onsio]. Erit quidem amplificatio eadem utrobique, sed lens S majorem feret aperturam quam dimidiam lentis α 6), tum quia lentis S foci distantia est 1/4 a, eoque major quam 1/2 foci distantiae lentis α, quae est 1/3 a; tum quia radius DF convergens, minus colorabitur in transitu per lentem S, quam si axi parallelus incederet. Sed in D jam aliquem colorem traxit, sed parum, quia lentis K foci distantia est KV 7).    1)  Ce qui suit, jusqu'à la fin de cet alinéa, manque dans les manuscrits tels que nous les possédons. Nous l'avons emprunté à la p. 185 de l'édition de 1703 de la "Dioptrique" par de Volder et Fullenius et il nous semble probable qu'on a affaire à une reconstruction par les éditeurs [...].    2)  A l'exemple de de Volder et Fullenius ce dernier alinéa a été emprunté à une feuille du manuscrit qui n'était pas comprise dans la numération rouge des pages, apportée par Huygens. Aussi il semble que Huygens, s'il avait achevé sa "Dioptrique", l'aurait donné dans une forme plus soignée [...].    3)  On a KV = a  [... voir marge, p. 465].    4)  Puisque KS = SV, par construction; voir la p. 463.    5)  Toujours par construction.    6)  On peut remarquer ici que le champ de vision de la lunette à double oculaire dépend de l'ouverture de la lentille K et dans l'autre de celle de la lentille α. Si donc l'ouverture de la lentille S peut être prise plus large que la moitié de celle de la lentille α la lunette à double oculaire pourra embrasser un champ de vision plus étendu, puisque KD = 2 SF; ce qui est conforme à l'énoncé de la présente proposition.    7)  On doit avouer que ce qui précède ne donne, pour en dire le moins, qu'une explication imparfaite de l'achromatisme relatif qui est propre à l'oculaire de Huygens. [...]

[ 469 ]

[ v ]

Propositio V   Telescopij ex quatuor convexis compositi constructionem explicare, quo res visae erectae spectantur et magna copia.   Propter inversam positionem rei visae vix aliter utimur composito e duobus convexis quam ad sidera, quae non refert quo positu spectentur. Quaenam vero tunc proportio servanda sit postea dicetur [>]. Quomodo autem erigantur rursus imagines magnaque simul earum copia uno intuitu comprehendatur diversimode quaesitum fuit 3, 4, 5, et pluribus lentibus. Quae sine causa non sunt multiplicandae, quod et singularum materia et superficierum reflexiones radiorum partem intervertant. Paucioribus tamen quam quaternis optatum effectum consequi non licet. Etsi enim in eadem telescopij longitudine et situs erectus et eadem amplificatio et eadem copia simul visorum obtineri potest tribus [<] aeque ac quatuor lentibus, deterior tamen est trium compositio quam quaternarum, quia in illa lentes oculares, aut unam certe earum oculo proximam, e majoribus superficiei sphaericae portionibus constare necesse est ratione diametri aut foci distantiae, si eadem anguli visorij magnitudo praestanda sit. Hinc vero colore inficiuntur res visae et lineae rectae circa aperturae margines curvae apparent.   Quaternis igitur utendum est, ex quibus telescopium hoc modo componitur.

[ 471 ]

[ v ]

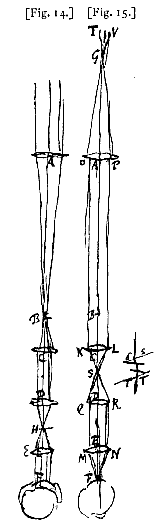Lens exterior est A, cujus foci distantia AB, in eodem vero axe positae sunt lentes oculares tres C, D, E prorsus aequales inter se, quarumque interior intervallo BC quantum est sua foci distantia ultra focum B removetur, ejusque intervalli duplum est a lente C ad lentem D, ac tantundem ab hac ad lentem E, ac denique ab hac ad oculum F rursus, quantum inter B et C.   Rursus autem binis figuris hic opus est, in quarum priore [Fig. 14] radij ab uno puncto rei longe distantis manantes exhibentur, quos facile apparet, si quis praecedentia perceperit, primum tanquam parallelos incidere in lentem A, inde colligi in B foco ejus, ac inde divergentes in lentem C incidere, quae denuo parallelos efficiat, mittatque ad lentem D, quae congreget eos ad focum suum H qui medium dividit intervallum DE. Tum denique ex H puncto ad lentem E tendentes ab ea tertio parallelos reddi atque ita ad oculum F accidentes distinctam visionem efficere cum in fundo ejus ad punctum unum cogantur.   In secunda figura [Fig. 15] consideratur ratio amplificationis quae est ea quae AB, foci distantiae lentis exterioris, ad foci distantiam BC, unius ex ocularibus. Ac praeterea anguli visorij amplitudo hic demonstratur. Positis enim ocularium trium aperturis aequalibus quae non majores sint apertura lentis exterioris A, ducantur MQ, NR axi communi parallelae et aperturae diametros lentium E et D comprehendentes. itemque KO, LP eidem axi parallelae et comprehendentes aperturam lentis KL, et posita AG aequali AB, ducantur rectae OGV, PGT quae sese intersecent in G. Jam patet latitudinem rei visae longinquae quae oculo nudo ex puncto G, ideoque et ex F, cerneretur in angulo TGV, hanc oculo per telescopium intuenti, occupare angulum MFN, ideoque augmenti rationem esse eam quae anguli MFN ad ang. TGV sive PGO, hoc est, eam quae intervalli AG ad intervallum EF, cum PO, MN, sint aequales; hoc est, eam quae foci distantia AB ad foci distantiam BC. quod erat dem.   Apparet porro angulum visorium MFN eandem quoque visibilium latitudinem comprehendere ac telescopium quod binis lentibus A et C constaret, cum res visa quae angulo TGV intercipitur, in illo telescopio spectetur in angulo KSL ipsi MFN aequali.

[ 473 ]

[ v ]

Haec egregia lentium compositio Romae nescio a quo primum fuit inventa*), multum tamen adjuta annulo seu diaphragmate quod ad H, loco medio inter lentes E D, vel ad B focum communem lentium A et C inseritur, cujus usum non ante cognitum explicuimus in libro de causis phaenomenon Saturni°). Est vero longe praecipuus, cum in metiendis planetarum diametris ut ibi docui, tum ad alia de quibus agam in sequentibus'). In hisce vero telescopijs circulum apparentium imaginum praeciso ambitu iste annulus ideo circumscribit, quod quae circa H vel B collocantur distincte cernuntur oculo F, cum radij ab H vel B egressi paralleli ad eum deferantur. Simul vero colores circa margines ejus opera resecantur, qui non bene antea vitari poterant.   Ponenda autem apertura annuli ipsarum lentium ocularium aperturis paulo minor, diameterque ejus ad ocularium foci distantiam certa ratione referendus, quae circiter ea est, quae ... ad ... docente nimirum experientia [43 : 110]. Quaenam vero sit ponenda proportio foci distantiae lentis exterioris ad foci distantiam ocularium quantâque aperturâ lucem admittere possit lens illa in sequentibus definietur [>].   Mirum videtur in hoc telescopio colores iridis oriri plurium ocularium refractione, non magis quam cum una ocularis adhibetur. Sed ratio haec est quod lens QR corrigit et aufert colores quas lens KL produxit. Idem enim accidit radio OKRN per superficies inclinatas ad K ac deinde ad R, transeunti, ac si per cuneos binos contrarie positos SS, TT transiret parallelis lateribus, qui colore non inficitur, non magis quam si per laminam vitream incederet.   *)  Giuseppe Campani.   °)  Systema Saturnium, p. 82. [ Voir la figure de Auzout, 1667, celle de R. Hooke (d'après Gascoigne) dans Phil. Tr. 1667, p. 541-4 et celle de P. Petit dans J. des Sç. 1667, p. 106b.]   ')  On n'en trouve rien dans ce qui suit dans la "Dioptrique".