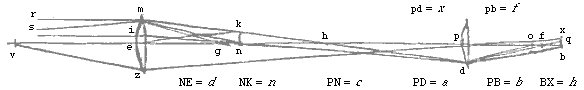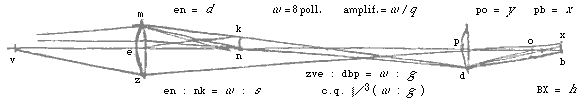Waarmee nu, zoals eerder over de hoeken GSI en GDH, volgens dezelfde methode aangetoond zal worden dat de hoeken BSL en BDF in dezelfde drievoudige verhouding zijn van de afstanden SP en PD. Want deze hoeken, of BST en BDQ, worden geacht zich te verhouden als BT tot BQ, omdat DP en SP heel klein zijn ten opzichte van BP. Nu is de verhouding BT tot BQ dezelfde als die samengesteld uit de verhoudingen TB tot BL, en BL tot BF, en BF tot BQ. En hiervan is de eerste, TB tot BL, dezelfde als die van SP tot PL, of die van SP tot PB, omdat LB heel klein is ten opzichte van PB. Evenzo is de andere verhouding BL tot BF dezelfde als die van het vierkant van PS tot het vierkant van PD, zoals even hiervoor is aangetoond. En de derde BF tot BQ is dezelfde als die van FD tot PD, dat is die van BP tot PD, omdat FB heel klein is ten opzichte van BP.
Daarom zal de verhouding BT tot BQ samengesteld worden uit de verhoudingen SP tot PB, en PB tot PD, en het vierkant van PS tot het vierkant van PD. En daar de eerste twee hiervan de verhouding SP tot PD geven, zal de verhouding BT tot BQ, dat is van hoek BSL tot BDF, zijn die van kubus PS tot kubus PD; wat nog te bewijzen was.
Voorstel XVIII
Hoe kortere microscopen te maken zijn, en meer vergrotende, met handhaving van dezelfde helderheid en scherpte, en die toch niet onderhevig zijn aan het genoemde nadeel van een grotere afwijking ten gevolge van de lensvorm. *)
Nu moet herhaald worden de figuur van het vorige onderzoek [<], en alles hetzelfde als daar gelezen wordt, tot aan de woorden:
|
Maar omdat ik nu de halve opening pd = x stel, en niet = fa/b
|
waarna we nu als volgt doorgaan.°)
 *) Ed. de Volder & Fullenius, p. 253 [fig.]; cf. p. 553, n. 4.
*) Ed. de Volder & Fullenius, p. 253 [fig.]; cf. p. 553, n. 4.
°) "zal gelden volgens de voorafgaande hulpstelling", etc. Deze aanwijzing wordt hier gevolgd [tekst tussen {}-tekens], naar het voorbeeld van de Volder en Fullenius.
{ Laat weer twee microscopen gesteld worden, en alles hetzelfde als in het voorstel [XIV], behalve dat onbepaald is, in de kleinste, de verhouding pb tot de halve opening pd; en eveneens onbepaald de brandpuntsafstand ne van de oculairlens. Maar laat al het overige op dezelfde manier geconstrueerd zijn. Verder is in de grootste microscoop de afstand PB = b, waarmee namelijk het lensje P van het object verwijderd is. PN = c; NE = d. Van de halve opening is de breedte PD = a. De lengte van het object is BX = h, NK = n.
Verder stellen we dat de afstanden PN en PB van bij elkaar behorende punten een verhouding hebben van groter dan 6 of 7 tot 1, en dat de brandpuntsafstand EN groter is dan de brandpuntsafstand PO. zoals deze in dergelijke microscopen gewoonlijk behoren vastgesteld te worden. Maar in de kleinere microscoop nemen we de afstand pb = f ; en de gezochte halve opening pd = x.
Nu zal pn = cf/b zijn omdat we PB, PN en pb, pn evenredig stellen.
Maar als zou gelden: zoals BP tot PD, zo bp tot pd, blijkt dat pd = fa/b zou worden, en de afwijkingshoek bdq, van de straal komend uit n naar lens p, zou gelijk worden aan de afwijkingshoek BDQ van de straal komend uit N naar lens P: omdat zoals in het vorige voorstel ook hier geldt: zoals NP tot np, zo PB tot pb, en zo ook de brandpuntsafstand PO tot po. }
|
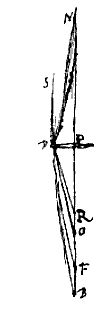 Als nu vanaf een punt N op de as een straal ND loopt naar dezelfde lens, die verstrooid door de breking de rode straal laat gaan naar B, en de uiterste violette naar F, zeg ik dat de hoek BDF te beschouwen is als gelijk aan de hoek ODR, en des te beter naarmate de helling van de lensoppervlakken in D een kleinere hoek heeft, en naarmate de punten B en O minder ver van elkaar af staan.
Als nu vanaf een punt N op de as een straal ND loopt naar dezelfde lens, die verstrooid door de breking de rode straal laat gaan naar B, en de uiterste violette naar F, zeg ik dat de hoek BDF te beschouwen is als gelijk aan de hoek ODR, en des te beter naarmate de helling van de lensoppervlakken in D een kleinere hoek heeft, en naarmate de punten B en O minder ver van elkaar af staan.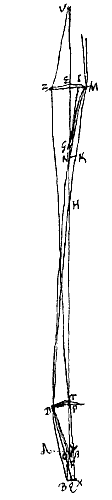 Nu zullen we de genoemde berekening als volgt behandelen. Van de lens P, waarvan we de dikte verwaarlozen, was de brandpuntsafstand PO = 7/10 van een duim, en PD = 1/20 . We trekken DO. Nu staat vast, als een straal die evenwijdig is met de as van bovenaf bij D invalt, dat deze verstrooid moet worden over de hoek ODβ, die 1/50 van hoek DOP is, zoals we gezegd hebben toen we de kleurschifting van een straal beschreven hebben [
Nu zullen we de genoemde berekening als volgt behandelen. Van de lens P, waarvan we de dikte verwaarlozen, was de brandpuntsafstand PO = 7/10 van een duim, en PD = 1/20 . We trekken DO. Nu staat vast, als een straal die evenwijdig is met de as van bovenaf bij D invalt, dat deze verstrooid moet worden over de hoek ODβ, die 1/50 van hoek DOP is, zoals we gezegd hebben toen we de kleurschifting van een straal beschreven hebben [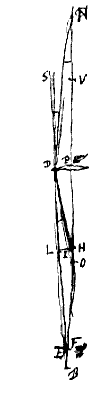 Zij van de lens PD de as NPB, brandpunt in O. SD een straal evenwijdig aan de as, die na breking gaat langs DH, de afwijking OH makend. Laat verder vanaf het punt N op de as naar dezelfde lens een straal ND lopen, die na breking samenkomt met de as in F, en B zij het punt dat met N verbonden is, en zo is van straal ND de afwijking FB.
Zij van de lens PD de as NPB, brandpunt in O. SD een straal evenwijdig aan de as, die na breking gaat langs DH, de afwijking OH makend. Laat verder vanaf het punt N op de as naar dezelfde lens een straal ND lopen, die na breking samenkomt met de as in F, en B zij het punt dat met N verbonden is, en zo is van straal ND de afwijking FB. 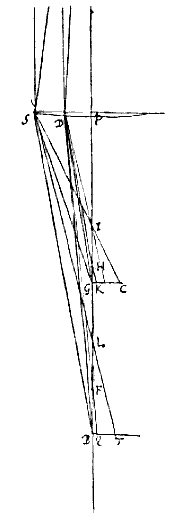 Van de lens PS zij de as PB, het brandpunt G, namelijk van de stralen evenwijdig met de as die daar heel weinig vandaan zijn. De lensdikte is te verwaarlozen, omdat de hele PS zeer klein gedacht wordt vergeleken met PB.
Van de lens PS zij de as PB, het brandpunt G, namelijk van de stralen evenwijdig met de as die daar heel weinig vandaan zijn. De lensdikte is te verwaarlozen, omdat de hele PS zeer klein gedacht wordt vergeleken met PB.  *) Ed. de Volder & Fullenius, p.
*) Ed. de Volder & Fullenius, p.