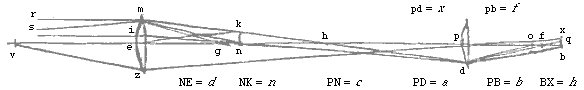Voorstel X
Principe en gebruik van enkelvoudige microscopen. De werking van van een lensje wordt gemakkelijk begrepen uit wat we over de vergroting van een bolle lens in het algemeen geschreven hebben (voorstel II.III). Want laat de lens zijn N, hetgene dat gezien wordt bij R, en wel in het brandpunt daarvan, en het oog O, zo dicht mogelijk naar de lens gebracht. Nu worden stralen die uit R gegaan zijn en gebroken, evenwijdig naar het oog gezonden, en ze geven scherp zicht. Verder wordt het zichtbare voorwerp QRQ onderscheiden met dezelfde grootte als wanneer de lens N er niet zou zijn, en als in plaats ervan een plaatje met een klein gaatje opgesteld zou worden [<], en wel onder de hoek QNQ. Zodat dus de tussengeplaatste lens hier niets anders verschaft, dan dat het zicht scherp wordt, terwijl het zonder de lens vaag zou zijn.
De werking van van een lensje wordt gemakkelijk begrepen uit wat we over de vergroting van een bolle lens in het algemeen geschreven hebben (voorstel II.III). Want laat de lens zijn N, hetgene dat gezien wordt bij R, en wel in het brandpunt daarvan, en het oog O, zo dicht mogelijk naar de lens gebracht. Nu worden stralen die uit R gegaan zijn en gebroken, evenwijdig naar het oog gezonden, en ze geven scherp zicht. Verder wordt het zichtbare voorwerp QRQ onderscheiden met dezelfde grootte als wanneer de lens N er niet zou zijn, en als in plaats ervan een plaatje met een klein gaatje opgesteld zou worden [<], en wel onder de hoek QNQ. Zodat dus de tussengeplaatste lens hier niets anders verschaft, dan dat het zicht scherp wordt, terwijl het zonder de lens vaag zou zijn. Maar met het blote oog wordt het pas zo scherp als het oog op enige afstand er vandaan staat, reken maar 8 duim. Nu kan men zeggen dat het beeld zoveel keer vergroot verschijnt, als die 8 duim groter zijn dan het afstandje NR, oftewel de brandpuntsafstand van het lensje N. En als deze gelijk is aan het vijfde deel van een duim, zal de lineaire vergroting zijn als 40 tot 1. Hoe kleiner dus de brandpuntsafstand van het lensje N is, des te groter is de uitwerking ervan bij het uitbreiden van de gedaante van een klein ding; hoewel zich hier enige hindernissen voordoen (in het vervolg te vermelden [>]) die niet toestaan dat we voorbij bepaalde grenzen gaan.
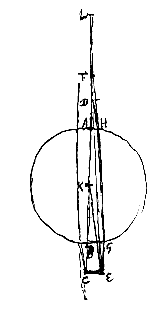 De werking van een bolletje, en wat we net gezegd hebben over een driemaal zo kleine afstand, wordt aangetoond als volgt:
De werking van een bolletje, en wat we net gezegd hebben over een driemaal zo kleine afstand, wordt aangetoond als volgt: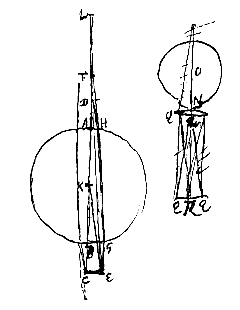 Daaruit vloeit voort dat, met het oog geplaatst in D (of waar dan ook op de doorgetrokken as BA, door voorstel II.
Daaruit vloeit voort dat, met het oog geplaatst in D (of waar dan ook op de doorgetrokken as BA, door voorstel II.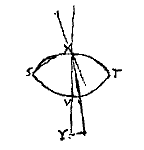 De dikte van de lens NQ hebben we hier op nul gesteld, een juiste schatting wanneer de brandpuntsafstand NR van een duim is, of niet veel minder. Maar aangezien in het gebruik heel kleine lensjes de beste zijn, zoals die waaraan men aan weerskanten vorm geeft met een bolvormige holte ['schoteltje' (
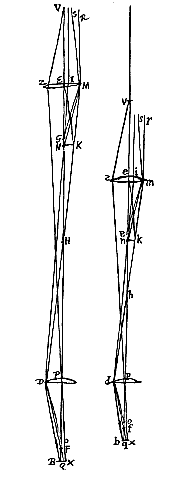
De dikte van de lens NQ hebben we hier op nul gesteld, een juiste schatting wanneer de brandpuntsafstand NR van een duim is, of niet veel minder. Maar aangezien in het gebruik heel kleine lensjes de beste zijn, zoals die waaraan men aan weerskanten vorm geeft met een bolvormige holte ['schoteltje' ( *) In de marge staan twee figuren, waarin te herkennen zijn het genoemde gaatje en de lichtbundel door een punt van het object midden in het gezichtsveld. Het is duidelijk dat de kleine doorsnede van deze bundel, waar hij het bolletje treft, in het bijzonder de twee lensafwijkingen [sferische en chromatische aberratie] vermindert, maar ook dat dit middel niet van toepassing is in het geval van een ondoorzichtig voorwerp dat van voren belicht wordt — zoals Huygens even later ook opmerkt.
*) In de marge staan twee figuren, waarin te herkennen zijn het genoemde gaatje en de lichtbundel door een punt van het object midden in het gezichtsveld. Het is duidelijk dat de kleine doorsnede van deze bundel, waar hij het bolletje treft, in het bijzonder de twee lensafwijkingen [sferische en chromatische aberratie] vermindert, maar ook dat dit middel niet van toepassing is in het geval van een ondoorzichtig voorwerp dat van voren belicht wordt — zoals Huygens even later ook opmerkt.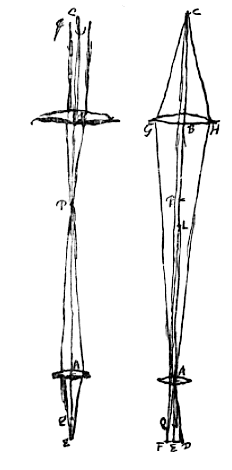 In de eerste zijn er stralen die zich uit één punt E van het object uitbreiden naar de lens A, door de breking hiervan samenkomen in punt P, en elkaar daar snijden, en dan doorgaan naar de lens B; door de werking hiervan worden ze evenwijdig gemaakt en zo komen ze aan bij het oog in C, en daardoor wordt het zicht scherp.
In de eerste zijn er stralen die zich uit één punt E van het object uitbreiden naar de lens A, door de breking hiervan samenkomen in punt P, en elkaar daar snijden, en dan doorgaan naar de lens B; door de werking hiervan worden ze evenwijdig gemaakt en zo komen ze aan bij het oog in C, en daardoor wordt het zicht scherp. 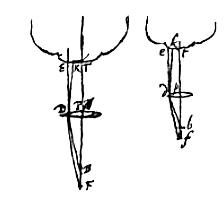
 Als gegeven is een willekeurige microscoop, samengesteld uit twee lenzen, volgens wat we gezegd hebben [
Als gegeven is een willekeurige microscoop, samengesteld uit twee lenzen, volgens wat we gezegd hebben [