1) De Latijnse tekst van deze verhandeling is vrijwel conform met die van p. 401-428 van de Opuscula postuma van 1703 (zie noot 1 van p. xii van T. XIII). We bezitten het Manuscript van de hand van Huygens, waaraan deze tekst is ontleend, uitgenomen veranderingen van interpunctie en enkele andere veranderingen, toevoegingen en weglatingen. Deels herstellen we de interpunctie van Huygens en in de noten vermelden we de veranderingen en weglatingen als ze niet geheel onbetekenend zijn; de toevoegingen zijn soms zeer aanzienlijk (zie het Voorbericht, p. 238), we zetten ze tussen haken.
 Het genoemde Manuscript van Huygens maakt deel uit van een verzameling losse bladen [HUG 26, 3r-17v] waarvan de pagina's door Huygens zijn genummerd van 1 tot 28. De eerste is door Huygens gedateerd op 21 okt. 1659. We geven de inhoud ervan in Aanhangsel I, evenals die van de andere die niet hier in de verhandeling staan. De theorema's daarin tonen dat de theorie van de centrifugale kracht al zeer ver ontwikkeld was. Ditzelfde wordt bewezen door enkele kanttekeningen in Manuscript A [HUG 10] (zie over dit Manuscript p. 4 van T. XV); meer daarover in Aanhangsel V hierna. We menen dus dat de verhandeling in hoofdzaak dateert van 1659.
Het genoemde Manuscript van Huygens maakt deel uit van een verzameling losse bladen [HUG 26, 3r-17v] waarvan de pagina's door Huygens zijn genummerd van 1 tot 28. De eerste is door Huygens gedateerd op 21 okt. 1659. We geven de inhoud ervan in Aanhangsel I, evenals die van de andere die niet hier in de verhandeling staan. De theorema's daarin tonen dat de theorie van de centrifugale kracht al zeer ver ontwikkeld was. Ditzelfde wordt bewezen door enkele kanttekeningen in Manuscript A [HUG 10] (zie over dit Manuscript p. 4 van T. XV); meer daarover in Aanhangsel V hierna. We menen dus dat de verhandeling in hoofdzaak dateert van 1659. Behalve de uitgave van 1703 bestaat er een herdruk in het tweede deel van de Opera reliqua van 1728 (p. 107-134), een werk genoemd op p. ii van het voorwoord van T. I.
2) Deze zin [op H.12], door een andere hand toegevoegd (evenals het woord 'dus' van de volgende zin), werd ontleend aan een ander blad dan de rest van deze pagina. Men leest er van de hand van Huygens [H.14]: "Zwaarte is de neiging naar beneden te gaan. En zware dingen gaan naar beneden met een versnelde beweging volgens de oneven getallen vanaf de eenheid 1, 3, 5, 7". Waarna Huygens laat volgen: "Dus wanneer iets zwaars", enz. (zie de tweede alinea van p. 257).
3) Het gaat om de 'Giornata terza' van de Discorsi e dimostrazioni matematiche, intorno à due nuove scienze van 1638, zie p. 212-213 van T. VIII (1898) vande nationale editie van Le opere di Galileo Galilei [Engl., bij Theorem II, exp. hellend vlak].
4) Zie p. 381-397 van T. I, Pars Post. Liber IX, Caput XVI van Almagestum novum, werk van 1651, aangehaald in noot 7 van p. 402 van ons T. I [p. 385: toren].
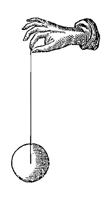
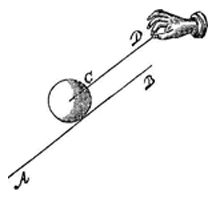 Nu kan met een beweging die volgens de genoemde groei wordt versneld, in dezelfde tijd een grotere of kleinere afstand worden afgelegd. Zoals wanneer iets zwaars op een hellend vlak AB op zijn plaats wordt gehouden door een draad CD die evenwijdig is aan dat vlak. Want ook hier tracht het zware ding voort te gaan langs de lijn DC met een op dezelfde manier versnelde beweging, maar niet zodanig dat het evenveel afstand doorloopt in een bepaald stukje tijd, als het zou doorlopen in hetzelfde stukje wanneer het van de loodrechte draad was losgelaten. Vandaar dat hier ook een kleinere neiging wordt gevoeld, die namelijk zoveel maal kleiner is dan die andere loodrechte neiging, als de afstand kleiner is waarover het zware ding op het hellend vlak zou gaan dan op de loodlijn, in dezelfde tijd 5).
Nu kan met een beweging die volgens de genoemde groei wordt versneld, in dezelfde tijd een grotere of kleinere afstand worden afgelegd. Zoals wanneer iets zwaars op een hellend vlak AB op zijn plaats wordt gehouden door een draad CD die evenwijdig is aan dat vlak. Want ook hier tracht het zware ding voort te gaan langs de lijn DC met een op dezelfde manier versnelde beweging, maar niet zodanig dat het evenveel afstand doorloopt in een bepaald stukje tijd, als het zou doorlopen in hetzelfde stukje wanneer het van de loodrechte draad was losgelaten. Vandaar dat hier ook een kleinere neiging wordt gevoeld, die namelijk zoveel maal kleiner is dan die andere loodrechte neiging, als de afstand kleiner is waarover het zware ding op het hellend vlak zou gaan dan op de loodlijn, in dezelfde tijd 5).
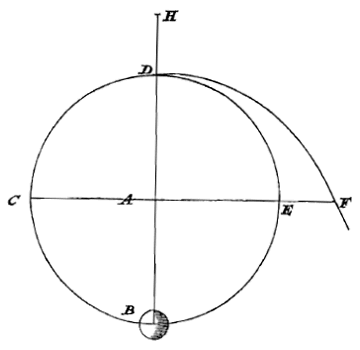
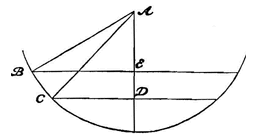
 Want bijvoorbeeld als een bol B hangt aan een draad AB, doch raakt aan de zijkant van een hol oppervlak CD, maar zo, dat de lijn vanaf het middelpunt van bol B naar het contactpunt loodrecht staat zowel op draad AB als op de raaklijn aan de kromme 1), dan weten we dat de bol nu helemaal niet wordt omhooggehouden door het oppervlak CD, maar dat hij even hard trekt aan het touw AB als wanneer hij het vlak CD niet zou raken maar vrij was opgehangen. Maar toch, als hij van het touw losraakt en neervalt, zal hij niet op dezelfde manier naar beneden gaan als wanneer hij vrij opgehangen het touw zou kwijtraken, maar hij zal, langs oppervlak CD naar beneden rollend, zeker niet de versnellingsverhouding volgens de oneven getallen 1, 3, 5, 7 nauwkeurig aanhouden. Dus blijkt dat er niet moet worden gelet op wat met het zware ding zal gebeuren enige tijd na het losraken van het touw, maar we moeten een willekeurig klein tijdsdeeltje beschouwen vanaf het begin van de beweging, als we de kracht van de neiging willen bepalen. En hier begint bol B, na het losraken van het touw, zo te bewegen zoals wanneer het loodrecht was neergevallen, aangezien hij aanvankelijk die bewegingsneiging heeft die volgens de rechte AB is, aangezien deze evenwijdig is aan de raaklijn aan de kromme in C.
Want bijvoorbeeld als een bol B hangt aan een draad AB, doch raakt aan de zijkant van een hol oppervlak CD, maar zo, dat de lijn vanaf het middelpunt van bol B naar het contactpunt loodrecht staat zowel op draad AB als op de raaklijn aan de kromme 1), dan weten we dat de bol nu helemaal niet wordt omhooggehouden door het oppervlak CD, maar dat hij even hard trekt aan het touw AB als wanneer hij het vlak CD niet zou raken maar vrij was opgehangen. Maar toch, als hij van het touw losraakt en neervalt, zal hij niet op dezelfde manier naar beneden gaan als wanneer hij vrij opgehangen het touw zou kwijtraken, maar hij zal, langs oppervlak CD naar beneden rollend, zeker niet de versnellingsverhouding volgens de oneven getallen 1, 3, 5, 7 nauwkeurig aanhouden. Dus blijkt dat er niet moet worden gelet op wat met het zware ding zal gebeuren enige tijd na het losraken van het touw, maar we moeten een willekeurig klein tijdsdeeltje beschouwen vanaf het begin van de beweging, als we de kracht van de neiging willen bepalen. En hier begint bol B, na het losraken van het touw, zo te bewegen zoals wanneer het loodrecht was neergevallen, aangezien hij aanvankelijk die bewegingsneiging heeft die volgens de rechte AB is, aangezien deze evenwijdig is aan de raaklijn aan de kromme in C. 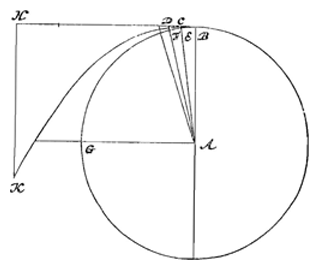
 3) Te weten de neiging zich achtereenvolgens te verwijderen over de afstanden EC en FD. Om nu deze conclusie nog duidelijker te maken schreef Huygens in de kantlijn:
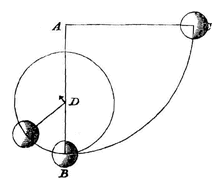
3) Te weten de neiging zich achtereenvolgens te verwijderen over de afstanden EC en FD. Om nu deze conclusie nog duidelijker te maken schreef Huygens in de kantlijn: 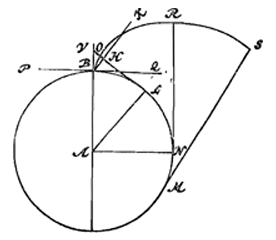 Als namelijk in B aan het wiel raakt een vlak PQ, dat eraan vastzit en samen met het wiel ronddraait, zal de bol B, als hij van het wiel of van het genoemde vlak losraakt, ten opzichte van dit vlak en punt B, die verder blijven bewegen, de kromme BRS beschrijven, die in B raakt aan de meegevoerde en verlengde straal AB.
Als namelijk in B aan het wiel raakt een vlak PQ, dat eraan vastzit en samen met het wiel ronddraait, zal de bol B, als hij van het wiel of van het genoemde vlak losraakt, ten opzichte van dit vlak en punt B, die verder blijven bewegen, de kromme BRS beschrijven, die in B raakt aan de meegevoerde en verlengde straal AB. 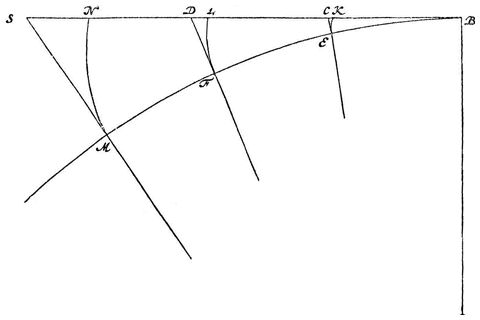
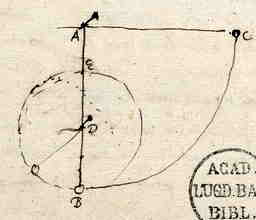
 Laat gegeven zijn cirkels met de stralen AB en AC, waarover twee gelijke voorwerpen in gelijke tijden worden rondgevoerd 1). Op beide worden heel kleine gelijkvormige bogen BD en CE aangenomen, en op de raaklijnen in de punten B en C worden BF en CG elk gelijk aan hun bogen genomen. Het op de cirkel BD rondgevoerde voorwerp heeft dus de neiging van het middelpunt weg te gaan langs het verlengde van zijn draad met een natuurlijke versnelde beweging en bij deze beweging over de afstand DF te gaan, in een bepaald tijdsdeel; doch het op de cirkel CE rondgaande voorwerp heeft wel een dergelijke neiging om van het middelpunt weg te gaan, maar daardoor legt het in datzelfde tijdsdeel de afstand EG af. Dus hoeveel maal zo groot DF is als EG, met een zoveel maal zo grote kracht wordt aan de draad getrokken op de grootste cirkel, als op de kleinste; nu blijkt FD tot GE te zijn zoals BF tot CG, dat wil zeggen zoals BA tot AC. Dan zal de centrifugale kracht op de grootste omtrek, | {p.
Laat gegeven zijn cirkels met de stralen AB en AC, waarover twee gelijke voorwerpen in gelijke tijden worden rondgevoerd 1). Op beide worden heel kleine gelijkvormige bogen BD en CE aangenomen, en op de raaklijnen in de punten B en C worden BF en CG elk gelijk aan hun bogen genomen. Het op de cirkel BD rondgevoerde voorwerp heeft dus de neiging van het middelpunt weg te gaan langs het verlengde van zijn draad met een natuurlijke versnelde beweging en bij deze beweging over de afstand DF te gaan, in een bepaald tijdsdeel; doch het op de cirkel CE rondgaande voorwerp heeft wel een dergelijke neiging om van het middelpunt weg te gaan, maar daardoor legt het in datzelfde tijdsdeel de afstand EG af. Dus hoeveel maal zo groot DF is als EG, met een zoveel maal zo grote kracht wordt aan de draad getrokken op de grootste cirkel, als op de kleinste; nu blijkt FD tot GE te zijn zoals BF tot CG, dat wil zeggen zoals BA tot AC. Dan zal de centrifugale kracht op de grootste omtrek, | {p. 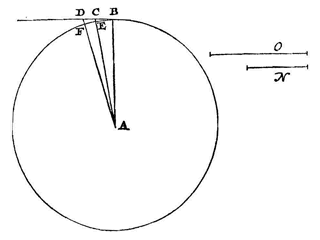
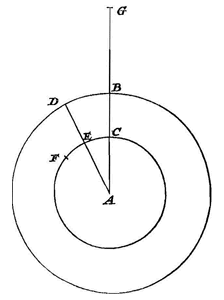 Laat om hetzelfde middelpunt A gelijke cirkels gegeven zijn, waarvan de stralen zijn AB en AC; en op hun omtrekken bewegen gelijke voorwerpen met gelijke snelheid, dat wil zeggen zó, dat in de tijd waarin op de grotere cirkelomtrek een boog BD wordt doorlopen, in dezelfde tijd op de kleinere wordt doorlopen de boog CF, in lengte gelijk aan die BD. Ik zeg dat de centrifugale kracht van het voorwerp dat op de omtrek BD ronddraait, zal zijn tot die welke het op omtrek CF rondgedraaide voorwerp heeft, als de straal AC tot AB.
Laat om hetzelfde middelpunt A gelijke cirkels gegeven zijn, waarvan de stralen zijn AB en AC; en op hun omtrekken bewegen gelijke voorwerpen met gelijke snelheid, dat wil zeggen zó, dat in de tijd waarin op de grotere cirkelomtrek een boog BD wordt doorlopen, in dezelfde tijd op de kleinere wordt doorlopen de boog CF, in lengte gelijk aan die BD. Ik zeg dat de centrifugale kracht van het voorwerp dat op de omtrek BD ronddraait, zal zijn tot die welke het op omtrek CF rondgedraaide voorwerp heeft, als de straal AC tot AB. 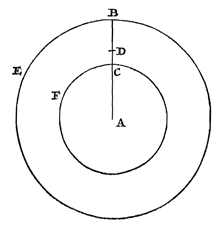 Laat gegeven zijn de ongelijke cirkels BE en CF om hetzelfde middelpunt A, waarvan de stralen zijn AB en AC; en op elk van beide draait een voorwerp, zodanig dat de centrifugale kracht voor beide gelijk is; ik zeg dat de tijd waarin cirkelomtrek BE wordt doorlopen, tot de tijd waarin omtrek CF wordt doorlopen, in tweedemachts-wortelverhouding is van AB tot AC, dat wil zeggen zoals BA tot AD die de middelevenredige is tussen AB en AC.
Laat gegeven zijn de ongelijke cirkels BE en CF om hetzelfde middelpunt A, waarvan de stralen zijn AB en AC; en op elk van beide draait een voorwerp, zodanig dat de centrifugale kracht voor beide gelijk is; ik zeg dat de tijd waarin cirkelomtrek BE wordt doorlopen, tot de tijd waarin omtrek CF wordt doorlopen, in tweedemachts-wortelverhouding is van AB tot AC, dat wil zeggen zoals BA tot AD die de middelevenredige is tussen AB en AC. 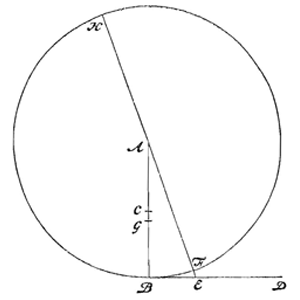
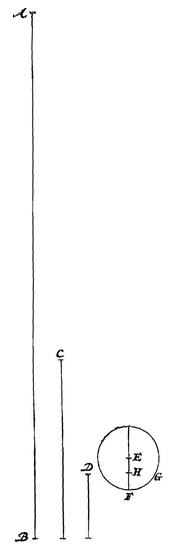 Laat gegeven zijn de hoogte AB, waarover een vallend voorwerp daalt vanuit rust in een tijd van bijvoorbeeld een seconde. Laat gelden: zoals een cirkelomtrek is tot zijn middellijn, zo is AB tot de lijn C, en zo is deze tot een derde D. En laat beschreven worden een cirkel EFG met de middellijn gelijk aan die D; ik zeg dat dit de cirkel is die verlangd wordt.
Laat gegeven zijn de hoogte AB, waarover een vallend voorwerp daalt vanuit rust in een tijd van bijvoorbeeld een seconde. Laat gelden: zoals een cirkelomtrek is tot zijn middellijn, zo is AB tot de lijn C, en zo is deze tot een derde D. En laat beschreven worden een cirkel EFG met de middellijn gelijk aan die D; ik zeg dat dit de cirkel is die verlangd wordt. 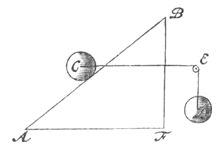 Als een gewicht C op zijn plaats wordt gehouden op een hellend vlak AB door een gewicht D dat vrij hangt, en als het touw CE evenwijdig met de horizon is, zal de zwaarte van D tot die van C zijn zoals de loodlijn BF tot de basis FA. Dit staat in de Mechanica vast. Hieruit volgt: als BF gelijk gesteld wordt aan FA, zal de zwaarte van D gelijk moeten zijn aan die van C.
Als een gewicht C op zijn plaats wordt gehouden op een hellend vlak AB door een gewicht D dat vrij hangt, en als het touw CE evenwijdig met de horizon is, zal de zwaarte van D tot die van C zijn zoals de loodlijn BF tot de basis FA. Dit staat in de Mechanica vast. Hieruit volgt: als BF gelijk gesteld wordt aan FA, zal de zwaarte van D gelijk moeten zijn aan die van C. 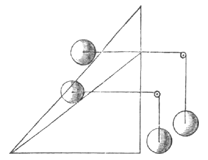 Als gelijke gewichten op vlakken die verschillend hellen op hun plaats worden gehouden, tegengehouden langs lijnen die evenwijdig met de horizon zijn, zullen de machten die ze op hun plaats houden tot elkaar zijn zoals de tangensen van de hoeken, waarmee de vlakken hellen ten opzichte van het horizontale vlak.
Als gelijke gewichten op vlakken die verschillend hellen op hun plaats worden gehouden, tegengehouden langs lijnen die evenwijdig met de horizon zijn, zullen de machten die ze op hun plaats houden tot elkaar zijn zoals de tangensen van de hoeken, waarmee de vlakken hellen ten opzichte van het horizontale vlak. 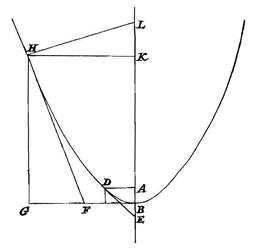 Laat nu gesteld worden dat een lichaam in D om de as wordt rondgevoerd met zodanige snelheid, dat de centrifugale kracht gelijk is aan de zwaarte; welke kracht dan, daar de hoek ADE de helft is van een rechte hoek, het lichaam op zijn plaats zal houden in het punt D {Lemm. I.}.
Laat nu gesteld worden dat een lichaam in D om de as wordt rondgevoerd met zodanige snelheid, dat de centrifugale kracht gelijk is aan de zwaarte; welke kracht dan, daar de hoek ADE de helft is van een rechte hoek, het lichaam op zijn plaats zal houden in het punt D {Lemm. I.}. 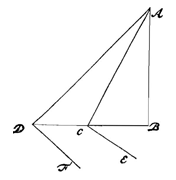 Laat eerst gesteld worden dat de voorwerpen gelijk zijn; laat DE de loodlijn op AC zijn, en evenzo DF de loodlijn op AD. Dan staat vast dat het de centrifugale kracht van de voorwerpen is die de draden zo schuin uitgestrekt houdt; en daar voorwerp C door zijn zwaarte dezelfde neiging heeft naar beneden te gaan als wanneer het op vlak CE zou gaan liggen; maar de centrifugale kracht (waarmee het weg wil gaan van as AB langs BC) die zwaarteneiging tegengaat; is het noodzakelijk dat de genoemde centrifugale kracht gelijk is aan de macht waardoor voorwerp C op zijn plaats gehouden zou worden op hellend vlak CE, langs lijn BC evenwijdig met de horizon. Om dezelfde reden is het noodzakelijk dat de centrifugale kracht waardoor voorwerp D wordt omhooggehouden, gelijk is aan de macht waardoor ditzelfde voorwerp op zijn plaats gehouden zou worden op vlak DF langs een rechte, eveneens evenwijdig met de horizon.
Laat eerst gesteld worden dat de voorwerpen gelijk zijn; laat DE de loodlijn op AC zijn, en evenzo DF de loodlijn op AD. Dan staat vast dat het de centrifugale kracht van de voorwerpen is die de draden zo schuin uitgestrekt houdt; en daar voorwerp C door zijn zwaarte dezelfde neiging heeft naar beneden te gaan als wanneer het op vlak CE zou gaan liggen; maar de centrifugale kracht (waarmee het weg wil gaan van as AB langs BC) die zwaarteneiging tegengaat; is het noodzakelijk dat de genoemde centrifugale kracht gelijk is aan de macht waardoor voorwerp C op zijn plaats gehouden zou worden op hellend vlak CE, langs lijn BC evenwijdig met de horizon. Om dezelfde reden is het noodzakelijk dat de centrifugale kracht waardoor voorwerp D wordt omhooggehouden, gelijk is aan de macht waardoor ditzelfde voorwerp op zijn plaats gehouden zou worden op vlak DF langs een rechte, eveneens evenwijdig met de horizon. 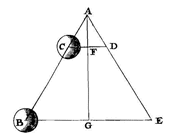 De centrifugale kracht is immers hetzelfde bij elk van zulke omlopen, om dezelfde schuine stand van de draad te houden. En als de genoemde kracht hetzelfde is, dan moet gelden: zoals de kwadraten van de tijden waarin de cirkels worden afgelegd, zo zijn de afstanden vanaf de omloopsas, volgens de omgekeerde IV 3). Dus hier: zoals CF tot BG, dat is zoals AC tot AB, zo zullen de kwadraten van de omlooptijden zijn. [Q.E.D.]
De centrifugale kracht is immers hetzelfde bij elk van zulke omlopen, om dezelfde schuine stand van de draad te houden. En als de genoemde kracht hetzelfde is, dan moet gelden: zoals de kwadraten van de tijden waarin de cirkels worden afgelegd, zo zijn de afstanden vanaf de omloopsas, volgens de omgekeerde IV 3). Dus hier: zoals CF tot BG, dat is zoals AC tot AB, zo zullen de kwadraten van de omlooptijden zijn. [Q.E.D.]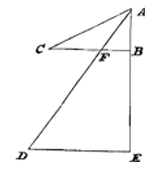 Laat de draden zijn AC en AD, en laat de daaraan vastgeknoopte voorwerpen C en D horizontale cirkels beschrijven, terwijl de uiteinden van de draden in A onbeweeglijk blijven. En laat C de draad AC trekken volgens het oppervlak van een kegel waarvan AB de as is, D op zijn beurt de draad DA langs het oppervlak van een kegel waarvan AE de as is. Ik zeg dat de omlooptijd van voorwerp C is tot de omlooptijd van voorwerp D in tweedemachts-wortelverhouding is van AB tot AE.
Laat de draden zijn AC en AD, en laat de daaraan vastgeknoopte voorwerpen C en D horizontale cirkels beschrijven, terwijl de uiteinden van de draden in A onbeweeglijk blijven. En laat C de draad AC trekken volgens het oppervlak van een kegel waarvan AB de as is, D op zijn beurt de draad DA langs het oppervlak van een kegel waarvan AE de as is. Ik zeg dat de omlooptijd van voorwerp C is tot de omlooptijd van voorwerp D in tweedemachts-wortelverhouding is van AB tot AE. 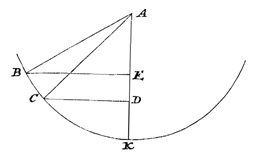
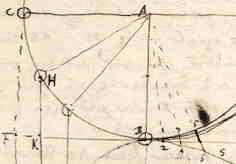
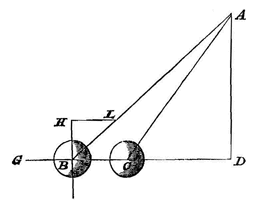 [Gegeven twee slingers met gelijk gewicht, AB en AC, en verschillende lengte, aan de uiteinden B en C waarvan twee opgehangen gelijke gewichten worden rondgedraaid om de gemeenschappelijke as AD. Ik zeg | {p.
[Gegeven twee slingers met gelijk gewicht, AB en AC, en verschillende lengte, aan de uiteinden B en C waarvan twee opgehangen gelijke gewichten worden rondgedraaid om de gemeenschappelijke as AD. Ik zeg | {p. 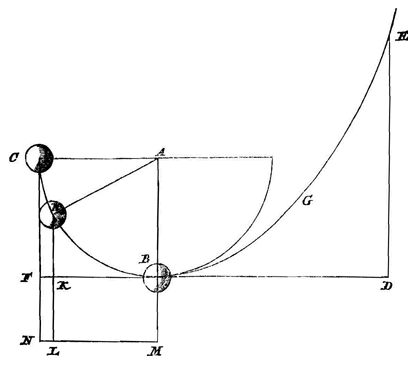
 2) In het Ms.: "langs de rechte te bewegen".
2) In het Ms.: "langs de rechte te bewegen".