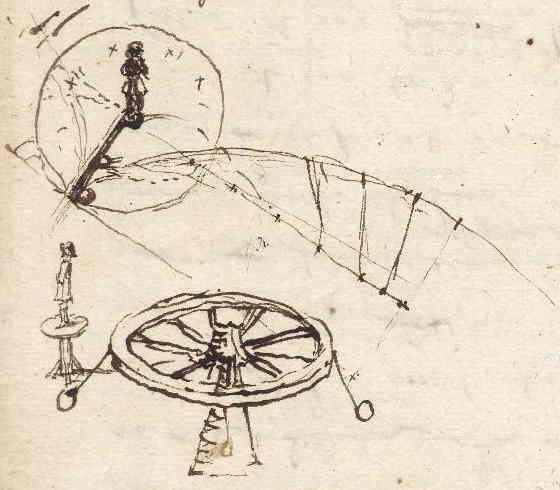
Vrij stapte ik de leegte in, als eerste 3).
| 21 Oct. 1659. |
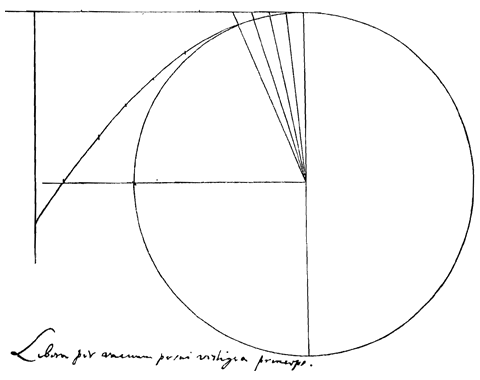
| [Fig. 1.] 4) |

|
| Libera per vacuum posui vestigia princeps. Vrij stapte ik de leegte in, als eerste 3). |
|
1) In dit Aanhangsel gven we de eerste bladzijden weer van het Manuscript van Huygens genoemd in noot 1 van p. 254 [hier 255], die met uitzondering van § 9 (p. 306) niet zijn gepubliceerd door de uigevers van Opuscula postuma [1703]. 2) Het in noot 1 genoemde Manuscript [HUG 26, 4r] begint met enkele aantekeningen die we bijeengebracht hebben in dit eerste deel, met het vers van Horatius als eerste. 3) Horatius, Epist. Lib. I, 19, vs. 21. [Vertaling: Kees Andriesse, NRC, 29 juni 1995. Het vers komt voor in werk van vader Constantijn Huygens, zie Forum der Letteren, 1967, p. 15.] 4) In Fig. 1 stelt de parabolische lijn ongetwijfeld een 'osculerende' parabool van de cirkel voor [driepuntig rakend]. Vergelijk Fig. 4 van p. 263 en Fig. 22 van p. 297. |
[ 303 ]
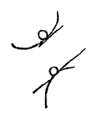 Om de kracht van de neiging te leren kennen moet bekeken worden wat er zal gebeuren als de bol wordt losgemaakt. En wel alleen wat er terstond na het losmaken zou gebeuren, zoals ook bij iets zwaars dat op een hol oppervlak is geplaatst, waarbij gekeken wordt naar de raaklijn aan dit oppervlak.
Om de kracht van de neiging te leren kennen moet bekeken worden wat er zal gebeuren als de bol wordt losgemaakt. En wel alleen wat er terstond na het losmaken zou gebeuren, zoals ook bij iets zwaars dat op een hol oppervlak is geplaatst, waarbij gekeken wordt naar de raaklijn aan dit oppervlak. Het naar beneden gaan volgens 1, 3, 5, 7 enz. wordt bevestigd door Riccioli, in boek 9 5). Over het nauwkeurig meten met de slingeringen van een uurwerk 6).
1. Laat gelden: zoals een middellijn is tot een cirkelomtrek, zo is deze tot een derde; en in het tijdsdeeltje waarin een zwaar ding, van een hoogte vallend, de lengte van de genoemde derde doorloopt, in hetzelfde tijdsdeeltje wordt een zwaar ding éénmaal rondgedraaid in een horizontaal vlak, waarin het wordt gehouden door een touwtje vastgebonden aan een pin, van welk touwtje de lengte moet zijn de helft van de genoemde middellijn; dan wordt met evenveel kracht aan het touwtje getrokken door de neiging van het zware ding om van het middelpunt weg te gaan, als er door hetzelfde zware ding aan getrokken zou worden wanneer het eraan was opgehangen, te weten door zijn eigen zwaarte 8). 5) Riccioli ... Almagestum novum [1651, zie p. 255, noot 4] heeft zelf talloze experimenten gedaan, vanaf verschillende torens van Bologna (p. 385). Ze lieten hem zien dat de "verhouding van de snelheidstoename zoals beweerd door Galilei" (p. 386) juist is: de in gelijke tijden doorlopen afstanden groeien aan "als 1. 3. 5. 7. 9. 11. &c.". 6) Vergelijk de noten 1 bij p. 279 en 281. 7) De tekst volgt op die van het eerste deel. 8) Deze paragraaf laat zien dat Huygens al in oktober 1659 de absolute grootte van de centrifugale kracht kende. Als r de straal is (en de lengte van het touw), is de 'derde' lengte l = 2π²r, en daar l = ½gt² (waarin t de omlooptijd is) komt er t = 2π√r/g, dus de snelheid v = √gr, dus mg (hier de centrifugale kracht) = mv²/r. Weliswaar gaat het in deze paragraaf slechts over een bijzonder geval, maar in de drie volgende paragrafen blijkt dat in de gedachte van de schrijver de centrifugale kracht mv²/r is voor willekeurige waarden van v en r. |
[ 304 ]
|
2. Hieruit volgt, als dit zo is, en we willen vervolgens omlopen die tweemaal zo lang duren, zodanig dat dezelfde trekkracht wordt behouden, dat we een touwtje moeten gebruiken dat viermaal zo lang is.*) 3. Als we willen dat een loden balletje, of iets anders dat zwaar is, steeds in één seconde wordt rondgevoerd in een horizontaal vlak, en even hard trekt als wanneer het aan het touwtje hangt, wordt gevraagd welke lengte het touwtje zou moeten hebben waaraan het vastgebonden balletje ronddraait. Antwoord: een balletje dat van een hoogte valt gaat in één seconde 14 voet 1) naar beneden, dus als de middellijn van een wiel, of tweemaal de lengte van het touwtje, gelijk is aan x, zal de omtrek zijn 22/7 x volgens Archimedes, waarbij de derde evenredige 484/49 x gelijkgesteld moet worden aan 14 voet; wat geeft x = 1 voet 5 duim en 1/121 duim, waarvan dus de helft 8½ duim + 1/142 2) de gevraagde lengte van het touwtje is. 4. En hoe groot als we willen dat het in 24 uur éénmaal wordt rondgevoerd? .... 5|290|250|579 v. is de straal of de lengte van het touwtje 3).
dan ontbreekt slechts dat zware dingen door het draaien van de aarde worden weggeslngerd, al zullen ze pas dan alle zwaarte verliezen als de halve middellijn van de aarde 265 5) keer zo groot zou zijn als nu. Maar nu verliezen lichamen 1/265 deel van de zwaarte als ze zich op de evenaar bevinden, voor andere is het minder.  [ *) HUG 26, 4r heeft nog een figuurtje bij § 2. Het zal een bovenaanzicht zijn, Huygens denkt aan een wiel (zie § 3). Een loshangend touw zou in beide gevallen een hoek van 45° maken met de as; vgl. § 10.]
[ *) HUG 26, 4r heeft nog een figuurtje bij § 2. Het zal een bovenaanzicht zijn, Huygens denkt aan een wiel (zie § 3). Een loshangend touw zou in beide gevallen een hoek van 45° maken met de as; vgl. § 10.] 1) Het gaat om Rijnlandse voeten, aangezien in § 4 hierna de middellijn van de aarde wordt uitgedrukt in Rl. voet. In okt. 1659 kende Huygens dus nog niet de juiste waarde van ½g, te weten (15 + 7½/12) Rl. voet (zie p. 280, n.1) In een kanttekening 'verbetert' hij het getal 14 zelfs in 13 8/12. [Deze waarde vond hij met een valproef op 23 okt. 1659, zie T. XVII, p. 278, met figuur] 2) Lees 1/242. 3) Weggelaten is berekening, waarin Huygens uitgaat van de waarde ½g = 14 voet. Hij merkt dan op: "Deze berekening zou ook verbeterd moeten worden door in plaats van 14 v. te stellen 13.8 d. of 13 2/3 voet". Hij voert deze berekening inderdaad uit en vindt nu een lengte van 5164292231 voet. 4) Vergelijk T. XV, p. 533, noot 3. Snellius drukt de middellijn van de Aarde uit in Rijnlandse roeden, Eratosthenes Batavus [1617], Lib. II, Cap. XII. 5) Het getal 265 (of liever 264) komt overeen met de lengte van de draad of straal in noot 3. Inderdaad geldt: 5164292231 : 19595160 = 263,5... [In werkelijkheid wordt gewichtloosheid bij een omlooptijd van 24 uur al bereikt op 6,6 keer de straal van de aarde (in de geostationaire baan), g is daar 40 keer zo klein als hier.] |
[ 305 ]
|
[ *) Huygens zag 'acceleratio' nog niet als de natuurkundige grootheid 'versnelling' (snelheidsverandering per seconde), het zijn de afstanden die toenemen volgens de groeiende rij.] 6) De tekst volgt op het vorige deel. In § 5-8 schetst Huygens het begin van een bewijs van het theorema in het 2e deel, zich baserend op het principe van het 1e: "Om de kracht van de neiging te leren kennen moet bekeken worden wat er zal gebeuren als de bol wordt losgemaakt. En wel alleen wat er terstond na het losmaken zou gebeuren". In § 6-8 geeft hij alleen met een figuur iets van een bewijs aan. Bij § 7 gaat het om de afwijking van de raaklijn (ook te veronderstellen bij § 6 en 8) en daar is, bij 'oneindig kleine' bogen, de afwijking bij de dubbele boog 4 keer zo groot als die bij de enkele; dan moet dus de kracht 4 keer zo groot zijn bij een dubbele snelheid. § 10 is een toepassing van het theorema van § 1. 7) Huygens voegt eraan toe: "Dit is hierna algemeen bewezen, zoals ook de twee volgende". Vergelijk de proposities I, II en III van de gepubliceerde verhandeling (p. 267-271). |
[ 306 ]
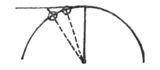 7. Als de snelheid van het omwentelen wordt verdubbeld, wordt een trekking teweeggebracht die vier keer zo groot is als eerst.
7. Als de snelheid van het omwentelen wordt verdubbeld, wordt een trekking teweeggebracht die vier keer zo groot is als eerst.
1) Vergelijk p. 281; deze § 9 is niet anders dan Lemma I van de uitgevers. 2) In plaats van 9½ had Huygens eerst geschreven: 8 3/10. De formule F = mv²/r laat zien, als het bolletje in rust is: CB = ½g × 1/(2π²). Voor CB = 8 3/10 duim en π = 22/7 vindt men ½g = 13 8/12 Rl. voet; voor CB = 9½ duim is ½g = 15 7½/12 Rl. voet. Vergelijk p. 280, n.1 [281] en p. 304, n.1. 3) Vergelijk § 13. In werkelijkheid is het evenwicht instabiel naar beide kanten, aangezien de centrifugale kracht vermindert als het bolletje daalt en toeneemt als het stijgt. 4) In plaats van 9½ had Huygens eerst geschreven 8 3/10. Vergelijk noot 2. |
[ 307 ]
|
Dus met dezelfde neiging om van het middelpunt weg te gaan waarmee bol B (wel op een wiel geplaatst) in staat is een zelfde bol D hangend te houden, zal hij ook zichzelf in de goot AB op zijn plaats kunnen houden.
5) Als de vergelijking van de parabool is y² = 2 px, heeft men voor x (BA) = ½p, AD (y) = p. 6) DE is de raaklijn aan de buitenste parabool in D, die BG snijdt onder een hoek van 45 °. 7) D.w.z. volgens Lemma I van p. 281; of liever volgens Lemma II dat eruit volgt. 8) Marge: "omdat namelijk DA = KL, als HL loodrecht op raaklijn HF is" [HUG 26, 5v: KL, niet CL]. 9) Als men aan een hellende buis precies de vereiste rotatiesnelheid kon geven, zou de bol op zijn plaats blijven. Huygens bedoelt dat dit evenwicht instabiel is, terwijl het in een kegelvormige holte stabiel is. |
[ 308 ]
|
maar wel gelijk, en daarom geldt volgens § 8 1): zoveel maal kleiner middellijn DC is als middellijn EF, zoveel maal kleiner zal de kracht zijn om van het middelpunt weg te gaan wanneer het over cirkel EF gaat, als over DC; maar op DC had het slechts genoeg om zich op zijn plaats te kunnen houden; en de helling van het vlak is dezelfde aan beide zijden.*) Dus op cirkel EF zal het zich niet op zijn plaats kunnen houden; en daarom zal het ook niet daarnaar stijgen. Anderzijds, als het naar beneden wil gaan naar cirkel GH zal het daarover in kortere tijd rondgaan dan op de vorige DC, aangezien het dezelfde snelheid houdt; dus zal het krachtiger van het middelpunt af willen gaan dan op cirkel DC, en de helling van het vlak is dezelfde*), dus daar het zich op cirkel DC op zijn plaats heeft kunnen houden, zal het niet kunnen blijven op de cirkel GH, maar stijgen naar waar het vandaan kwam. Het zal dus ook niet naar beneden gaan vanuit DC, behalve wanneer het geleidelijk snelheid verloren zal hebben, door het tegenkomen van lucht en door enige oneffenheid van het glas en van de bol.
1) De uitgevers hebben deze tekst niet gepubliceerd, maar wel '8' veranderd in 'prop. 3'. Vgl. p. 271, prop. III. [ *) O.C. mist het stukje (van HUG 26, 6v), "aan beide zijden ..." t/m "... de helling van het vlak is dezelfde":] |
| ... estque plani inclinatio utrobique eadem; Ergo in circulo EF se sustinere non poterit. quare neque eo ascendet. Rursus si descendere velit ad circulum GH, eum minori tempore circumibit quam priorem DC, quoniam celeritatem eandem retinet, ergo violentius à centro tendet quam in circulo DC, estque plani inclinatio eadem; ergo cum in DC ... |
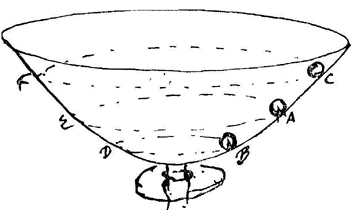
| 14. Hetzelfde gebeurt in een parabolische schaal. En het mooie is bij zo'n schaal of spiegel die parabolisch is, dat een bol die daarin rondgaat alle omwentelingen isochroon heeft, op welk plek hij ook loopt. |
|
Er is hier immers voor de bol dezelfde kracht nodig om zich op zijn plaats te houden als in de parabolische goot 2). Als hij dus in kortere tijd de cirkel BD af zou leggen dan tevoren de cirkel AE, zou hij meer kracht hebben dan om zich op cirkel BD te kunnen houden, en daarom zou hij stijgen. Doch de stelling is dat hij niet stijgt, maar op cirkel BD rondgaat. Dus legt hij de cirkel BD niet in een kortere tijd af dan AE. Maar ook niet in een langere, aangezien dan voor hem de neiging van het middelpunt weg te gaan niet voldoende zou zijn om zich op de cirkel BD te houden, en daarom zou hij naar beneden gaan naar een kleinere cirkel. Doch de stelling is dat hij op BD draait; dan zal hij deze dus ook niet in een langere tijd afleggen dan cirkel AE. Dus blijkt dat hij beide doorloopt in dezelfde tijd, en om dezelfde reden welke andere cirkel in de schaal dan ook. Met een heel kleine beweging van de schaal, zodanig dat het onderste punt een klein cirkeltje beschrijft, kan de beweging van het bolletje worden voortgezet; en als hiervan de omlopen worden geteld, zal op deze wijze een precieze meting van de tijd worden verkregen, nauwkeuriger dan met een slinger. En als ½ latus rectum van de parabool gelijk is aan 9½ duim 3) zullen de omlopen elk in een seconde worden uitgevoerd. Als je in plaats van een parabolische spiegel een bolvormige neemt met een straal van 9½ duim 3) zul je 2) Vgl. § 11. 3) I. p. v. 9½ had Huygens eerst geschreven 8 3/10. Vgl. p. 306, n.2. |
[ 309 ]
|
bijna hetzelfde effect zien, maar de omlopen zullen toch iets sneller zijn, en het meest die, welke het wijdst zijn. Ik beschouw een of ander heel klein bolletje, want anders zal wegens de grootte ervan de verhouding zelfs bij de parabolische vorm niet helemaal volmaakt zijn, maar grotere bollen zullen iets vlugger rondlopen.
4) Huygens voegt in de marge toe: "Dit heb ik later beter behandeld." Vergelijk Prop. X, p. 287, waaruit die van de tekst onmiddellijk volgt. 5) In de marge: 9½. Vergelijk noot 2 van p. 306. 6) Dat wil zeggen: a : √(ab) = 1" : x, dus x = √(ab)/a of √(b/a). |
[ 310 ]
|
zal zijn √(c/a), dan zal dit de gevraagde zijn. Dat wil zeggen als geldt: zoals BG of GA is tot de middelevenredige tussen GA en HA, zo is 1" tot een andere; dan zal dit de tijd zijn waarin een omloop in K moet worden voltooid, opdat het bolletje zich daar op zijn plaats kan houden.
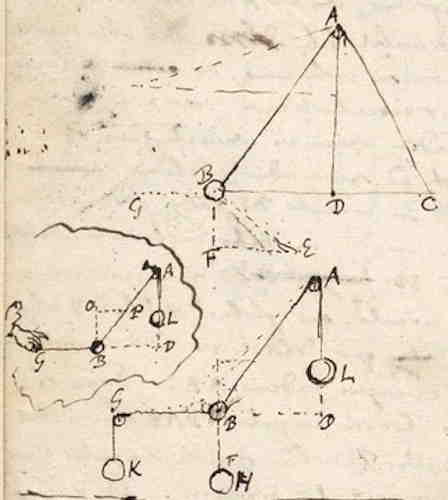
De centrifugale kracht waarmee de bol zich op zijn plaats houdt is immers dezelfde als die waarmee hij zich op het vlak BE (loodrecht op AB) zou houden als eraan getrokken werd langs de rechte DBG. En hiervoor zou het nodig zijn dat aan een touw BG werd getrokken door een gewicht 1), dat tot de zwaarte van de bol zou zijn zoals BF tot FE, volgens § 9, met welk gewicht de centrifugale kracht nu equivalent is. En de bol zelf wordt door heel zijn zwaarte naar beneden getrokken langs de loodlijn BF. Hieruit volgt dat bij welke lengte dan ook van het touw AB, als de hoek van de kegel die dit touw beschrijft dezelfde is en het gewicht van B hetzelfde blijft, dezelfde trekking zal worden gevoeld in het draaipunt A 2). Overweeg slechts dat de neiging om van het middelpunt weg te gaan langs een horizontale lijn is zoals BG, en dat er daarom bij het draaien van de draad in de stand AB evenveel bij de zwaarte of trekking van gewicht B komt, als er zou bijkomen wanneer iemand dit met een horizontale draad BG in die stand zou houden 1), maar nu is bekend dat er dan bij de genoemde zwaarte 1) In de marge schets Huygens nog een iets andere figuur [zie hieronder]. Het gewicht K en het katrolletje in G zijn er vervangen door een hand die in de richting BG trekt. De letters O en P ervan zijn hier toegevoegd. 2) De alinea's die volgen zijn in het Manuscript in de marge geschreven. |
[ 311 ]
|
zoveel komt, dat het gewicht L nodig is om B in evenwicht te houden, zodat namelijk L tot B is zoals PB tot BO, dat is als BA tot AD. Dus blijkt dat door het gewicht B te draaien bij het spannen van AB een trekking in A wordt gevoeld zo groot als het gewicht L veroorzaakt wanneer het er gewoon aan hangt. Dus het is niet nodig vlak BE of gewicht K te beschouwen 3). |
|
3) Deze laatste opmerking laat zien, samen met die van de noten 7 van p. 305 en 4 van p. 309, waarom de uitgevers hebben gemeend § 1-8 en 10-17 te moeten weglaten. Huygens heeft de indeling in paragrafen nog voortgezet tot aan nummer 20. § 18 komt overeen met Prop. IX, p. 287 (en het bewijs ervan), § 19 met het bewijs van Prop. XVI (p. 297-299) en § 20 met het bewijs van Prop.XVII (p. 299-301). Vervolgens komen de beschouwingen over zwaarte waarmee de uitgevers de verhandeling laten beginnen.
|
[ 312 ]
bij 'De vi centrifuga'
[?] 2)

| 1. | Als een voorwerp op de omtrek van een cirkel beweegt, met de snelheid die het verkrijgt door te vallen van een hoogte die een vierde deel is van de middellijn, zal het de neiging om van het middelpunt weg te gaan gelijk hebben aan zijn zwaarte; dat wil zeggen, het zal de draad waarmee het wordt tegengehouden even sterk spannen, als wanneer het eraan is opgehangen 3). |

| 2. | Als twee gelijke voorwerpen met gelijke snelheid op ongelijke cirkels bewegen, zullen hun centrifugale krachten omgekeerd evenredig zijn met de middellijnen 4). |
| 3. | Als twee gelijke voorwerpen op gelijke cirkels ronddraaien, met ongelijke snelheden, maar beide met eenparige beweging, zal de centrifugale kracht van het snellere zijn tot de kracht van het langzamere, als de kwadratische verhouding van de snelheden 5). | |

| 4. | Als twee gelijke voorwerpen in gelijke tijden ongelijke cirkels doorlopen, zal de centrifugale kracht op de grootste cirkel zijn tot die op de kleinste, zoals de middellijn van de grootste cirkel tot de middellijn van de kleinste 6). |

| 5. | Als twee gelijke voorwerpen, ronddraaiend op ongelijke cirkelomtrekken, de centrifugale kracht gelijk hebben, zal de omlooptijd op de grootste omtrek zijn tot de omlooptijd op de kleinste, als de verhouding van de tweedemachtswortels van de middellijnen 7). |
1) Ontleend aan p. 43-45 van Manuscript 13, getiteld 'Excerpta ex Adversarijs Christiani Hugenij' [HUG 13, 22r-23r; eerste in Catalogue, p. 86], waarin Huygens gewoonlijk zijn voornaamste ontdekkingen schreef. Alle 13 theorema's behalve het 11e en 13e staan, meestal iets anders geformuleerd, in de verhandeling gepubliceerd door de Volder en Fullenius, zoals de volgende noten aanwijzen. Het 13e komt overeen met een alinea van het Manuscript (genoemd in noot 1 van p. 254/255) die niet is gepubliceerd. 2) Datering in Manuscript 13: 26 febr. 1663 op p. 15 en 5 mei 1673 op p. 48. 3) Zie p. 275, Prop. V. 4) Zie p. 271, Prop. III. 5) Zie p. 269, Prop. II. 6) Zie p. 267, Prop. I. 7) Zie p. 273, Prop. IV. |
[ 313 ]

| 6. | Als twee voorwerpen, hangend aan ongelijke draden, zo ronddraaien dat ze horizontale cirkels beschrijven, terwijl het andere uiteinde van de draad onbeweeglijk blijft, en als de hoogtes gelijk zijn van de kegels waarvan de draden bij deze beweging het oppervlak beschrijven, zullen ook de tijden gelijk zijn waarin elk van beide voorwerpen zijn cirkel doorloopt 8). | ||

| 7. | Als twee voorwerpen, hangend aan draden, al draaiend cirkels beschrijven evenwijdig aan de horizon, zullen de omlooptijden zijn in de verhouding van de tweedemachtswortels van de hoogtes van de kegels, waarvan de draden het oppervlak doorlopen 9). | ||
| 8. | Hieruit volgt, als een voorwerp hangend aan een draad, waarvan het andere uiteinde vast blijft, ongelijke cirkels beschreven heeft evenwijdig aan de horizon, dat de omlooptijden zullen zijn in de verhouding van de tweedemachtswortel van de sinussen van de hoeken waarmee de draad helt ten opzichte van het vlak van de horizon 10). | |||

| ||||

| 9. | Als bij zo'n draaiing de hoek, waarmee de draad helt ten opzichte van het horizonvlak, een halve rechte hoek is, zal de tijd van één omloop zijn tot de tijd van een loodrechte val van de halve hoogte van de kegel, beschreven door de draad, als van de cirkelomtrek tot de straal 11). | ||
| Het wordt bewezen met het feit dat het voorwerp in dit geval de centrifugale kracht gelijk moeten hebben aan zijn zwaarte, dat wil zeggen gelijk aan die welke het zou hebben gekregen door te vallen van de hoogte van een vierde deel van de middellijn van de cirkel die het beschrijft, volgens prop. 1 hierboven. | ||||
| | 10. | Uit de twee voorgaande wordt opgemaakt, wanneer een voorwerp aan een draad hangend de kleinste van alle mogelijke cirkels beschrijft, dat de tijd van één omloop tot de tijd van een loodrechte val vanaf de hoogte van die draad is, zoals de omtrek van een cirkel tot de zijde van het daarin ingeschreven vierkant. Dat de omlooptijd daarom gelijk is aan de kleinste slingertijd van dezelfde slinger, waarin deze heen en weer beweegt 12). | ||
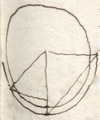
| 11. | Uit deze en de 8e wordt bewezen, als een zo opgehangen voorwerp een met de horizon evenwijdige cirkel beschrijft, dat de omlooptijd tot de tijd van een loodrechte val vanaf een hoogte gelijk aan de draad is, zoals de omtrek beschreven met een straal die middelevenredig is tussen de draadlengte en de hoogte van de kegel die de draad al draaiend beschrijft, tot die welke het dubbele van de draad vermag 13).
| |||
| ||||
|
8) Zie p. 285, Prop. VIII. 9) Zie p. 287, Prop. X. 10) Zie p. 289, Prop. XI. 11) Zie p. 291, het bewijs van Prop. XII (begin van de 2e alinea). 12) Zie p. 289, Prop. XII. 13) D.w.z. aan een lengte waarvan het kwadraat gelijk is aan 2× het kwadraat van de draadlengte. 14) Zie p. 293, Prop. XIV. |
[ 314 ]
 12. 12.
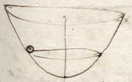
| In een holle parabolische conoïde, met de as loodrecht, worden alle omlopen van een bolletje, dat met de horizon evenwijdige cirkels doorloopt, of ze nu groot zijn of klein, in gelijke tijden afgelegd 1). |
| 13. | En indien het 'latus rectum' van de parabool 19 Rijnlandse duim is, zal elke omloop worden afgelegd in één seconde, als namelijk het bolletje heel klein wordt gedacht; want het middelpunt ervan moet zich noodzakelijk op het oppervlak van de conoïde bevinden. | |
| Dit wordt gehaald uit de 10e en uit het feit dat een slinger met een lengte van 9½ duim een dubbele slingering per seconde geeft, of ook een heel klein cirkeltje, zoals de ondervinding leert 2). |
|
1) Zie p. 281, Prop. VII. 2) Zie § 11, p. 307.
|
[ 315 ]
bij 'De vi centrifuga'
[In de vertaling van Horologium oscillatorium, deel 5.]
[ 319 ]
bij 'De vi centrifuga'
[1659] 2)
| de tijden van heen en weer bewegen van slingers zijn in de verhouding van de tweedemachtswortels van de lengten 3). |
| de tijden van horizontale kringlopen zijn in de verhouding van de tweedemachtswortels van de assen 4) der kegels die ze beschrijven 5). |
1) Ontleend aan p. 173 van Manuscript A [HUG 10, 87r]. 2) Op p. 158 van Manuscript A [HUG 10, 79v] vindt men de beschrijving van twee valproeven, waarbij Huygens gebruik maakt van een slinger ("Proef gedaan op 21 Oct. 1659" en "Proef gedaan op 23 Oct. 1659") [met een tekening, zie T. XVII, p. 278]. Op p. 175 vindt men de woorden "Uitgevonden op 5 Oct. 1659" [HUG 10, 88r; "Date very probably should read 5 Nov."] (het gaat om een uurwerk met kegelslinger). P. 176 [HUG 10, 88v] waarop een zelfde soort proef is beschreven als van 21 en 23 okt., heeft de datum 15 nov. 1659. We merken op dat Huygens op deze laatste datum zegt "uit de beweging van de kegelslinger" te hebben bepaald de tijd die nodig is voor een valvan een lichaam vanaf een bepaalde hoogte (de proef zal te vinden zijn in het volgende deel) [T. XVII, p. 281]. 3) Galilei kende deze eigenschap, als nauwgezet slinger-waarnemer. In Discorsi e dimonstrationi matematiche, Leiden 1638, leest men (p. 97): |
|
Sagredo: ... Ik heb wel duizend keer gelet op slingeringen, in het bijzonder van de lampen in een kerk, aan een heel lang koord hangend en onopzettelijk door iemand in beweging gebracht ... p. 96: Salviati: ... Over dalingen langs bogen ... toont ... de ondervinding dat ze alle in gelijke tijden verlopen ... En wat betreft de verhouding van de slingertijden van voorwerpen die aan draden van verschillende lengte hangen, deze tijden zijn in de verhouding van de tweedemachtswortels van de draadlengten, of laat ik zeggen de lengten zijn in de verhouding van de kwadraten van de tijden. |
|
In de nationale uitgave Le opere di Galileo Galilei vindt men deze passages op p. 140 en 139 van vol. VIII, 1898. (Huygens kan de dialogen van Galilei hebben gelezen in de uitgave van 1638, of in die van 1656, genoemd in T. I, p. 494, noot 1). In deze tijd deed Huygens proeven waarin de slinger een rol speelde, en hij heeft deze eigenschap van de gewone slinger toen misschien ook waargenomen. 4) Alternatieve lezing: "van de hoogtes". 5) Vergelijk Prop. IX op p. 287. Huygens kan het resultaat van deze berekening proefondervindelijk hebben geverifieerd. Het is ook mogelijk dat hij deze eigenschap van de kegelslinger (min of meer overeenkomend met die van de gewone slinger) waargenomen heeft alvorens er een theoretische verklaring voor te geven.
|
[ 320 ]
bij 'De vi centrifuga'
[1659] 2)
|
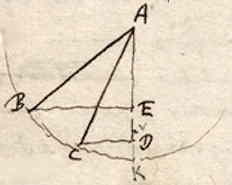
Zie de eerste figuur*) van de vorige pagina.
| |
| (1) | Laat ∠ BAE = 45° zijn. |
| (2) | voorwerp B moet de centrifugale kracht gelijk hebben aan zijn zwaarte; het moet met die snelheid rondgaan die het heeft na een val over de helft van AE of EB. |
| (3) | de tijd over AK tot de tijd volgens BE is als VA 3) tot omtrek EB. |
| (4) | maar de tijd volgens BE tot de tijd volgens K, dat is volgens de kleinst mogelijke cirkel, is als KA tot VA. |
| (5) | de tijd over AK tot de tijd volgens K is als KA tot omtrek EB. |
| (6) | maar de tijd over ½AK tot de tijd over AK is als BE of EA tot AK. |
| (7) | de tijd over ½AK tot de tijd volgens K is als BE tot omtrek BE, dat is als de straal tot de omtrek. |
| (8) | Dus de tijd van een heel kleine draaiing van slinger AK is gelijk aan een heel kleine slingering ervan 4). |
1) Ontleend aan Manuscript A, p. 177 [HUG 10, 89r]. Het blaadje waarop de figuur stond ontbreekt, evenals de vier voorgaande blaadjes. 2) P. 176 heeft de datum 15 nov. 1659, en p. 188 die van 15 dec. 1659. [ *) J. Yoder, Catalogue 2013, bij HUG 10, 89r: de figuur staat op HUG 26, 17v. Het is de figuur bij Prop. XI (p. 289), maar zonder de letter V die de uitgevers van Opuscula postuma (1703) niet overnamen; ze schreven in het handschrift "Fig. 19" naast de figuur en "Vide Fig. 19" naast de tekst.] 3) Zie de volgende noot (4e alinea van p. 322). 4) Propositie (8) komt overeen met Prop. XII van de verhandeling (p. 289): "Als een slinger, in kegelbeweging gebracht, zeer kleine omlopen maakt ... elk van de tijden ervan ... gelijk aan de tijd van twee zeer kleine zijwaartse slingeringen van dezelfde slinger." In (8) moet "heel kleine slingering" dus verstaan worden als de tijd van een heel kleine heen en weer beweging. | |
| Prop. XII van de verhandeling is (zoals we hebben gezegd op p. 281, n.4 en 317, n.6) door de uitgevers ontleend aan Horologium oscillatorium; zij hebben er een bewijs aan toegevoegd. | |
[ 321 ]
|
Nu lijkt de tekst van Prop. (8) van dit Aanhangsel meer op die van Theorema 10 van Manuscript No. 13 (p. 313 hierboven): "Dat de omlooptijd [in de kleinste van alle mogelijke cirkels] daarom gelijk is aan de kleinste slingering van dezelfde slinger, waarin deze heen en weer beweegt": hier wordt ook de tijd van een dubbele slingering aangeduid met de weinig exacte uitdrukking "oscillatio minima". Misschien kunnen we hieruit concluderen dat de proposities van Manuscript No. 13 eerder zijn geformuleerd dan de proposities van Horologium oscillatorium. |
| Dit Aanhangsel met het bewijs van Propositie (8) — de cijfers (1) ... (8) zijn door ons toegevoegd — werd ongetwijfeld voorafgegaan door andere bewijzen [inderdaad: die van Prop. I t/m XI, zie bij HUG 10, 88v: "Behind f. 88, eight folios removed: now HUG 26, ff. 10-17"]. Vergelijk p. 325, noot 6. Het is mogelijk dat de blaadjes die ontbreken door de Volder en Fullenius uit het boek werden genomen, en dat ze deze hebben gebruikt om hun bewijzen op te stellen van Prop. VII en XII-XV van de verhandeling; p. 177 en 178 [HUG 10, 89rv] bevatten nog andere berekeningen en kunnen daarom erin gelaten zijn. |
| Hoe het ook zij, de tekst van dit Aanhangsel en het bewijs van Prop. XII (p. 289-291) lijken sterk op elkaar. |
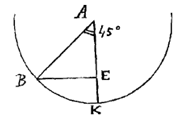 Fig. 20 (p. 293) bij het bewijs van de uitgevers doet ook dienst bij de volgende proposities; anders had ze de vorm kunnen hebben van de figuur hiernaast, die overeenkomt met de tekst van Huygens. De punten C en D van Fig. 20 komen overeen met onze punten B en E. Het laagste punt moet hier worden aangeduid met de letter K, zoals in Fig. 19 (p. 289).
Fig. 20 (p. 293) bij het bewijs van de uitgevers doet ook dienst bij de volgende proposities; anders had ze de vorm kunnen hebben van de figuur hiernaast, die overeenkomt met de tekst van Huygens. De punten C en D van Fig. 20 komen overeen met onze punten B en E. Het laagste punt moet hier worden aangeduid met de letter K, zoals in Fig. 19 (p. 289). Als r de straal BE is en l de draadlengte AK, leert vergelijking (6) ons dat dus l = r√2, overeenstemmend met de figuur hiernaast. |
| Vergelijking (5) wordt √(2l/g) : 2π√(l/g) = l : 2πr en er is aan voldaan: de uitdrukking "tijd volgens K" wordt uitgelegd in vergelijking (4) en bij "omtrek EB" gaat het om de omtrek waarvan EB de straal is. |
|
Aan vergelijking (7) is eveneens voldaan. Om van (7) naar (8) te gaan moet bekend worden verondersteld de vergelijking: (9) de tijd over ½AK tot de tijd van een heel kleine (dubbele) slingering is als de straal tot de omtrek, ook te schrijven als: (9') ¼ van de tijd van een heel kleine slingering (½ van een enkele slingering) tot de tijd over ½AK = halve omtrek tot middellijn. |
|
In deze vorm komt ze overeen met Prop. XXV van het Tweede deel van Horologium oscillatorium, waar gezegd wordt naar aanleiding van de cycloïdale slingering: "... zijn de daaltijden waarin een voorwerp ... het onderste punt van de top bereikt, onderling gelijk; en ze hebben tot de tijd van een loodrechte val over de hele as van de cycloïde de verhouding van de halve cirkelomtrek tot de middellijn". |
[ 322 ]
| Inderdaad is de as van de cycloïde gelijk aan de helft van de kromtestraal in het laagste punt. We weten overigens door een opmerking van Huygens op p. 188 van Manuscript A [HUG 10, 94v] dat Prop. XXV van het Tweede deel van Horologium oscillatorium hem bekend was voor 15 december 1659. |
| Vergelijking (4) is te schrijven als | √(2r/g) : 2π√(l/g) = l : VA |
| en vergelijking (3) als | √(2l/g) : √(2r/g) = VA : 2πr. |
| Uit elk van beide komt | VA = 2πr √√2. |
| De lengte VA, gelijk aan die van een omtrek met straal √(AE × AK), stond waarschijnlijk in de figuur van Huygens aangegeven met een hulprechte buiten de figuur, of veeleer met een rechte vanuit het middelpunt A [inderdaad dit laatste, zie de figuur hierboven op p. 320]. |
Laten we nu de vergelijkingen (2) ... (8) beschouwen in volgorde van de tekst. |
| Vergelijking (2) komt overeen met Prop. V (p. 275) van de verhandeling, of met Th. 1 van Manuscript No. 13 (p. 312). De uitgevers (p. 289-291) beginnen eveneens hun bewijs van Prop. XII uitgaande van Prop. V. |
|
Vergelijking (3) is te schrijven als: de tijd over AK is tot de tijd volgens BE als √√2 tot 1 of: de tijd over ½BE : de tijd over ½AK = 1 : √√2. |
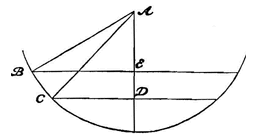 Ze komt dus overeen met de volgende zin van de uitgevers [zie Fig. 20 (van p. 291) hiernaast]:
Ze komt dus overeen met de volgende zin van de uitgevers [zie Fig. 20 (van p. 291) hiernaast]: "Nu is DA tot CA als 1 tot √2, zodat de tijd van een loodrechte val vanaf half DC tot de tijd van een loodrechte val vanaf half CA, welke tijden in wortelverhouding zijn van DC tot CA, zal zijn in de verhouding van 1 tot √√2." Vergelijking (4) is te schrijven, door de eerste en de derde term te delen door √2, als: de tijd over ½BE : de tijd volgens K = r : 2πr √√2. |
|
In deze vorm komt ze overeen met de volgende zin van de uitgevers (p. 291): "Dientengevolge is de tijd van een loodrechte val vanaf half DC, tot de tijd van een heel kleine rondgang, zoals de straal tot de omtrek vermenigvuldigd met √√2". |
|
Vergelijking (5), af te leiden uit de vergelijkingen (3) en (4), is te schrijven, door twee termen te vermenigvuldigen met √2, als: de tijd volgens K : de tijd over 2 AK = 2πr : 2r of: de tijd volgens K : de tijd over 2AK = 2πr√√2 : 2r√√2. |
|
Ze komt dus overeen met de volgende zin van de uitgevers: "dus is de tijd van een heel kleine rondgang van de slinger AC tot de tijd van een loodrechte val vanaf de dubbele slingerhoogte, zoals de omtrek vermenigvuldigd met √√2 tot het dubbele van de straal vermenigvuldigd met √√2, of zoals de omtrek tot de middellijn." |
| Vergelijking (7), af te leiden uit vergelijking (5) met behulp van de evidente vergeljking (6), is bijna identiek met vergelijking (5). |
|
Tenslotte veronderstellen de uitgevers als bekend Prop. XXV van het Tweede deel van Horologium oscillatorium (zie p. 291 n.2 en p. 282/283 n.3) en concluderen ze op dezelfde manier als Huygens tot gelijkheid van de omlooptijd volgens een heel kleine omtrek enerzijds en van de tijd van een heel kleine dubbele slingering anderzijds.
|
[ 323 ]
bij 'De vi centrifuga'
[Eerste deel] 2)
[1666] 3)
103005000 voet in 1 uur af te leggen met een gelijkmatige beweging 4) met de snelheid uit 1/4 van de middellijn van de aarde 5).
| |||||||||||
1) Ontleend aan Manuscript C, p. 89 en 90. 2) Ms. C, p. 89 [HUG 3, 45r]. 3) Ms. p. 79 heeft de datum 20 nov. 1665, en p. 92 is gedateerd "te Parijs 1666". 4) Huygens wil de rotatiesnelheid berekenen die de aarde zou moeten hebben om een voorwerp op de evenaar een centrifugale kracht te geven gelijk aan zijn zwaarte. Volgens Prop. V (p. 275) is hiervoor nodig de snelheid na een val over een 1/4 van de middellijn van de aarde. Hij vindt met een berekening die neerkomt op die van √(gR) (met R = straal van de aarde), 103005000 Rijnlandse voet per uur. Dit getal is veel te groot; Huygens had de meting van Snellius (p. 304) kennelijk niet bij de hand, hij neemt voor de middellijn van de aarde een waarde die 50% te groot is (zie p. 324, n.1). Voor ½g neemt hij 13.4.1 voet. Later schreef hij 15.7½ en de waarde van Snellius, zonder de berekening te verbeteren, Zie p. 326, n.4. 5) Huygens bedoelt met het getal 103005000 de snelheid van een voorwerp dat over 1/4 van de middellijn van de aarde is gevallen met de versnelling g. [ In het manuscript lijkt te staan "ex 1/4" i.p.v. " | |||||||||||
[ 324 ]
| Er zijn 36000 voeten in 1 duitse mijl 1). ... 8100000 voet legt een voorwerp op de evenaar af in 1 uur. |
| De snelheid dus die de centrifugale kracht gelijk zou maken aan de zwaarte is tot de snelheid waarmee een voorwerp op de evenaar gaat, als 1030 tot 81 ongeveer. |
| Maar de centrifugale krachten van voorwerpen die in gelijke cirkels rondgaan zijn tot elkaar als de kwadraten van de snelheden, dus |
| 1060900 : 6561 ongeveer als 165 2) tot 1. |
| Dus op de evenaar gaat er voor zware dingen meer dan 1/165 3) af van hun zwaarte, dat wil zeggen dat ze daar lichter zijn dan op de pool met 1/165 3) deel van hun gewicht. |
| Hoeveel op de breedte van 45 gr.? Dat wordt ongeveer 1/343 4). |
| 7 : 5 = 1/165 : 1/245. |
| 7 : 5 = 1/245 : 1/343. |
1) Hier tekent Huygens later aan: "juister 22800". Het is deze fout in de lengte van de duitse mijl (p. 88 van het Manuscript [HUG 3, 44v]: "36000 voet in een duitse mijl naar ik meen") die hem een te grote waarde gaf voor de middellijn van de aarde; zie p. 323, n.4. 2) Eerder 162. 3) Deze breuk werd verbeterd in 1/162. Een veel betere waarde (1/265) was door Huygens al in 1659 gevonden (p. 304). 4) Om dit getal te vinden moet 1/165 tweemaal achtereenvolgens worden vermenigvuldigd met ½√2 of 5/7, eenmaal omdat de straal van de beschreven cirkelomtrek 5/7 van die van de evenaar is, en eenmaal omdat de richting van de centrifugale kracht een hoek van 135° maakt met die van de zwaartekracht. Er zit een rekenfout in 7 : 5 = 1/165 : 1/245. Men zou 1/245 vinden als de vorige breuk 1/175 was. |
[ 325 ]
[1666]
| Op een andere manier hetzelfde als op de vorige pagina. |
| 9½ duim is gevonden in boek A voor de straal van de cirkel, waarvoor geldt dat, als een zwaar ding op de omtrek loopt en deze aflegt in de tijd van 1", de centrifugale kracht gelijk is aan de zwaarte 6). |
| lin. 114 7) | 61848x | lijnen bevat in 1/4 middellijn van de aarde 8). |
| 36000 | = x aantal voeten in een duitse mijl 9). | |
| 371088000 | ||
| 185544 | ||
| 2226528000 | lijnen in 1/4 middellijn van de aarde. |
| Ik had moeten zetten 1/2 middellijn van de aarde, maar het wordt hieronder verbeterd door vermenigvuldiging met 2. |
| 19530947 | 10) |
| 2 | |
| 39061894 | 11) |
| zoveel maal het gewicht van een zwaar ding zou gelijk zijn aan de centrifugale kracht op de evenaar als de aarde in 1 sec. zou omwentelen. |
5) Manuscript C, p. 90 [HUG 3, 45v]. 6) Zie p. 281. De betreffende berekening is niet meer te vinden in Ms. A [HUG 10; wel: HUG 26, 15v]; vergelijk hierover Aanhangsel V op p. 320, noot 4, vierde alinea van de noot. 7) 9½ duim = 9½ × 12 = 114 lijn [1 lijn = 1/12 duim]. 8) Huygens neemt hier voor de straal van de aarde 15 × 360 × 7/44 = 859 duitse mijlen. Als x het aantal Rijnlandse voeten is in een duitse mijl, wordt de halve straal van de aarde ½ × 144 × 859x = 61848x Rijnlandse lijnen. 9) Te groot getal; vergelijk noot 1 en noot 11 die volgt. 10) Dit is 2226528000 gedeeld door 114. 11) Het getal 39061894 (veel te groot) komt dus uit de deling van de lengte van de straal van de aarde, uitgedrukt in duim, door 9½. Zie voor verbetering van dit getal p. 326, noot 4. |
[ 326 ]
[?] 2)
| 28500 | roeden in een graad van omtrek aarde bij Snellius 3). |
| 12 | |
| 342000 | voeten |
| delen door 15 | mijl*) |
| 22800 | voeten in een duitse mijl. |
| Dus de wegwerpkracht zal iets kleiner zijn dan met de voorgaande berekening is gevonden 4). |
1) Manuscript C, p. 90 [HUG 3, 45v]. 2) De regels die volgen zijn later toegevoegd (andere inkt). 3) Eratosthenes Batavus, 1617, Lib. II, Cap. XII [zie p. 304, n.4]. [ *) HUG 3, 45v: "15 mill."] 4) Om het eerder gevonden getal 39061894 (p. 325) te verbeteren moet het dus worden vermenigvuldigd met 22800/36000, wat geeft 24739200. De centrifugale kracht op de evenaar zou dus gelijk zijn aan 24739200 maal de zwaarte als de aarde in 1 seconde zou ronddraaien. |
| Door dit getal te delen door (24 × 3600)² vindt men dat de centrifugale kracht bij de evenaar gelijk is aan 1/302 maal de zwaarte. Deze breuk is kleienr dan de breuk 1/265 die in 1659 is verkregen (p. 304) omdat op p. 281 de waarde voor ½g juist is (15 voet 7½ duim), terwijl Huygens bij de berekening van p. 304 had genomen ½g = 13 voet 8 duim (zie daar noot [1, 3 en] 5). |
| In de berekening hebben we met Huygens de straal van de aarde gelijk genomen aan 859 × 22800 = 19585200 Rijnlandse voet. Op p. 304 had Huygens met Snellius, die een nauwkeuriger waarde voor π gebruikt, genomen 19595160 voet. Op p. 91 van Manuscript C [HUG 3, 46r] schrijft Huygens: "3264500 roeden in de middellijn van de aarde". De straal van de aarde zou dan zijn 19587000 voet. In dat geval zou de centrifugale kracht op de evenaar gelijk zijn aan 24741474 maal de zwaarte als de aarde in 1 seconde zou ronddraaien. De breuk waarom het gaat wordt weer 1/302. Dezelfde waarde wordt gevonden door de berekening van het Eerste deel van dit Aanhangsel te verbeteren. |
| Later, in 'Discours de la cause de la pesanteur' van 1690 [Ned.] neemt Huygens met Picard de straal van de aarde = 19615800 Parijse voet = 144/139 × 19615800 = 20321404 Rijnlandse voet. Hij vindt dan (met toepassing van Prop. XIII, p. 291) voor de beschouwde breuk ongeveer 1/17² of 1/289. Volgens de methoden van dit Aanhangsel vindt men, voor deze waarde van de straal van de aarde, de breuk 1/291; maar door voor de rotatieperiode van de aarde de juistere waarde 23 h. 56 min. te nemen (zoals Huygens doet in genoemd Discours) vindt men precies 1/289.
|
[ 327 ]
bij 'De vi centrifuga'
[1668] 2)
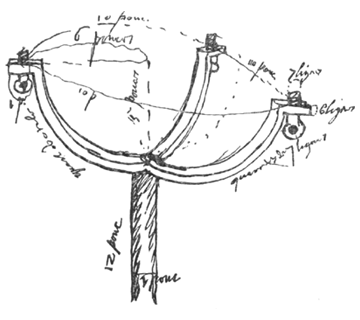
| Om een wiel van 3 voet middellijn op te zetten en een staaf 3) van 12 duim, in het midden doorboord, voor experimenten met de centrifugale kracht 4) |
1) Ontleend aan Manuscript C, p. 211 [HUG 3, 106r]. 2) Datum op p. 209 [105r, zie T. VI, 212*]: 21 juli 1668 [102r: 5 sept. 1667] en op p. 231 [116r]: 25 febr. 1668. 3) Dit woord [pertice] is niet echt Frans (we konden het onmogelijk anders lezen) en verwijst naar de 'pertica' of staaf van 12 duim die in de figuur is te zien en die het toestel ondersteunt. 4) We weten niet of het geschetste instrument ooit is gebouwd; de afmetingen zijn aangegeven in de figuur (bovendien leest men links "kwart cirkel" en rechts "kwarten van 7 lijn"). |
[ 328 ]
Zeker is dat Huygens dit soort proeven heeft gedaan. In zijn Discours de la cause de la pesanteur van 1690 staat op p. 130 [Ned.]: |
| Evenals ik heeft hij [Descartes] de neiging beschouwd van lichamen, die in een cirkel draaien, zich te verwijderen van het middelpunt; de ondervinding staat ons niet toe daaraan te twijfelen. Want bij het ronddraaien van een steen in een werpslinger voelen we dat hij aan onze hand trekt, en dit des te sterker naarmate we sneller draaien; zelfs zo sterk dat het touw wel eens kan breken. Ik heb eerder deze zelfde eigenschap van de cirkelbeweging laten zien, door zware lichamen aan te spannen op een rond blad, in het middelpunt doorboord, dat draaide op een spil; en ik heb gevonden hoe de kracht ervan te bepalen is, en verscheidene stellingen daarover, die te zien zijn aan het eind van het boek dat ik geschreven heb over de beweging van slingers [1673, p. 159]. |
| De proeven met de ronde tafel zijn in 1667 gedaan in Parijs: Huygens maakt er melding van in zijn brief van 2 dec. 1667 aan zijn broer Constantijn (T. VI, p. 164). |
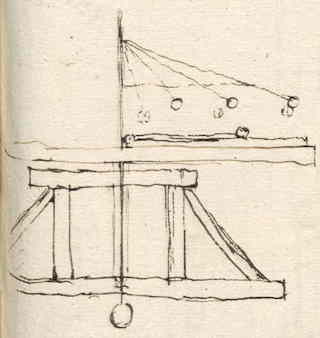
[ Op HUG 2, 110r), waarschijnlijk van 1669:]
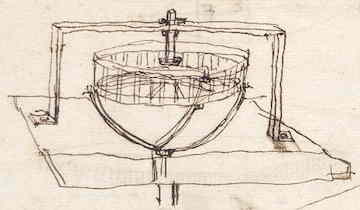
[ Op HUG 26A, 40v, misschien 1656:]