3. Aangezien de kanonnier me wel kan zeggen welke hoogte het kanon heeft boven de horizon: laat me weten of het 4 of 5 voet is, of minder, want dat is zo belangrijk voor . . . . . als het maar 4 voet boven de horizon is.
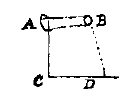 Ik bedoel met CD de horizon, het kanon AB horizontaal, als, zeg ik, CA of BD maar 4 voet is, en het zoals u zegt 398 passen draagt alvorens de grond te raken, dan zou, als CA of DB 16 voet hoog was, de kogel 796 passen gaan (te weten het dubbele), en als AC 64 voet boven de horizon was dan zou hij 4 keer zo ver gaan als bij een hoogte van slechts 4 voet. U ziet dus de noodzaak om de hoogte ervan boven de horizon te weten, die zodanig kan zijn dat het horizontale bereik langer is dan dat bij 45 graden.
Ik bedoel met CD de horizon, het kanon AB horizontaal, als, zeg ik, CA of BD maar 4 voet is, en het zoals u zegt 398 passen draagt alvorens de grond te raken, dan zou, als CA of DB 16 voet hoog was, de kogel 796 passen gaan (te weten het dubbele), en als AC 64 voet boven de horizon was dan zou hij 4 keer zo ver gaan als bij een hoogte van slechts 4 voet. U ziet dus de noodzaak om de hoogte ervan boven de horizon te weten, die zodanig kan zijn dat het horizontale bereik langer is dan dat bij 45 graden.
Wat betreft de passen: dat u zegt dat er 4 passen zijn in uw roede, dat is een beetje twijfelachtig, want probeert u zelf eens deze roede in 4 passen te doen, u zult de benen te wijd uiteen moeten zetten om zo ver te blijven lopen als het grote bereik is; dat echter wel gemeten zou moeten worden met uw roeden om zeker te zijn, een ketting of koord van zo'n 20 roeden . . . . . 2 jongens zouden dit bereik wel vlug gemeten hebben, en nog vlugger het horizontale, dat ongeveer het 10e of 11e deel ervan zou zijn.
Misschien zult u niet veel moeite behoeven te doen om uw bediener van het kanon daartoe over te halen, en zelfs om de proef te doen zoals ik zeg, dat zijn stuk als het 4 keer hoger boven de horizon staat, de kogel 2 keer verder zal zenden, want dat is nogal opmerkenswaardig.
4. Ik verzoek u, dat hij u weet te zeggen hoeveel de kogel van een batterijstuk verder gaat, zowel horizontaal als bij zijn grote bereik van 45 graden, dan genoemd stuk met kogels van 6 pond; dat zal hij kunnen . . . . ook proberen zoals bij de 1e poging.
Men zegt dat te Nancy een kanon met lange loop*) anderhalve mijl draagt in volle vlucht, wat vrijwel van Nancy tot St. Nicolas is; ik kan het moeilijk geloven, ik zal de waarheid ervan trachten te achterhalen, bij deze zelfde gelegenheid als die waarvoor ik u hier dit heb gevraagd en in de vorige brief°) die u naar ik meen tezelfdertijd zult ontvangen.
Wilt u me inlichten hoeveel een pond kwik kost in Holland, onze mensen verkopen het hier voor 45 stuivers, er zijn 16 ons in ons pond dat naar ik meen bij benadering gelijk is aan het uwe. De heer Descartes heeft me hier gezegd (naar me voorkomt) dat het in Holland maar 16 of 20 stuivers kost.
Ik had er hier bijna 30 pond van nodig om net de proef te laten doen.
Ik ben ervan verzekerd dat u, als u aanwezig bent bij de proef met het kanon, nog meer zult onderzoeken behalve wat ik ervan opgesteld heb; het zal nodig zijn 4 of 5 touwtjes van 3 voet te doen klaarmaken, elk met een musketkogel aan het eind, om de tijd goed te meten.
[ *) Coulevrine (Veldslang) de Nancy; Lat. colubra - (kleine) slang; 'culverina' genoemd in F. Marini Mersenni mimimi ballistica et acontismologia (Par. 1644), p. 82. De 'colubrina' komt voor in een tabel met gegevens over kanonnen in: Adriaan van Roomen, Universae mathesis idea (1602), p. 89.
Robert Norton, The gunner (1628), p. 42-: 'culvering', 'colubrine', 'couleuvrine', met figuren. Ons woord 'klovenier' is eruit ontstaan. ]
[ °) Misschien No. 41.]

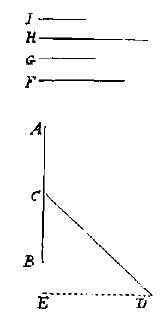 Laat de rechte AB, gelijk aan de middellijn van de basis van de gegeven scheve cilinder, doormidden zijn gesneden in C. Laat verder de rechte DC gelijk zijn aan de as daarvan; en de hoek DCB de helling van de as daarvan met het vlak van de basis.
Laat de rechte AB, gelijk aan de middellijn van de basis van de gegeven scheve cilinder, doormidden zijn gesneden in C. Laat verder de rechte DC gelijk zijn aan de as daarvan; en de hoek DCB de helling van de as daarvan met het vlak van de basis.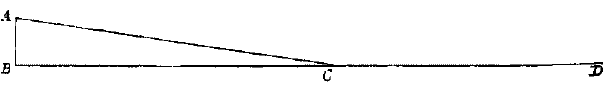
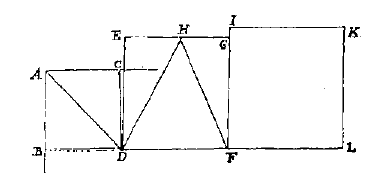 Hij veronderstelt dan dat met het vierkant, of liever de kubus ABCD gelijk aan 1, en met vierkant EDFG dubbel zo groot als vierkant ABCD (omdat ED gelijk is aan de diagonaal AD), als men de gelijkbenige driehoek DHF erin beschrijft, en men met FH als zijde de kubus IFKL maakt, dat deze kubus het viervoudige zal zijn van de eerste kubus ABCD. Zodat slechts te vinden overblijft de middelevenredige kubus tussen de kubus IL en de kubus AD, om de 2 middelevenredige kubussen te krijgen tussen 1 en 8. Laat u me uw mening daarover weten.
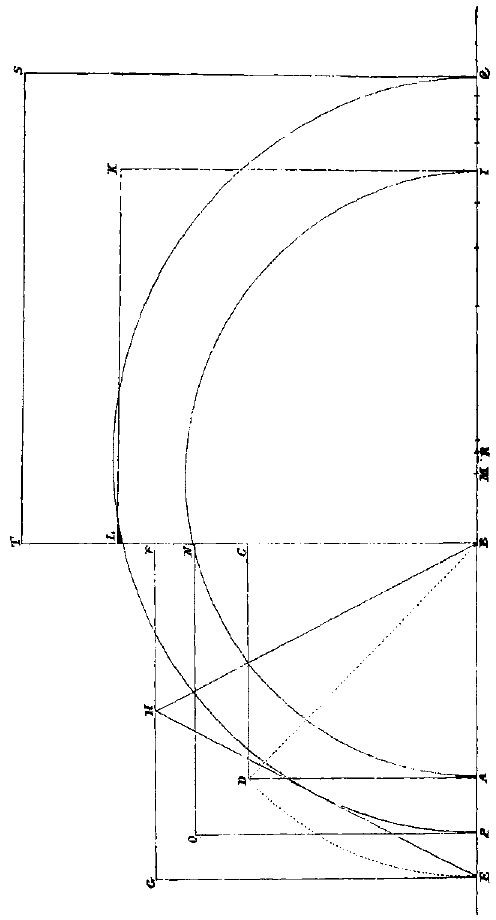
Hij veronderstelt dan dat met het vierkant, of liever de kubus ABCD gelijk aan 1, en met vierkant EDFG dubbel zo groot als vierkant ABCD (omdat ED gelijk is aan de diagonaal AD), als men de gelijkbenige driehoek DHF erin beschrijft, en men met FH als zijde de kubus IFKL maakt, dat deze kubus het viervoudige zal zijn van de eerste kubus ABCD. Zodat slechts te vinden overblijft de middelevenredige kubus tussen de kubus IL en de kubus AD, om de 2 middelevenredige kubussen te krijgen tussen 1 en 8. Laat u me uw mening daarover weten.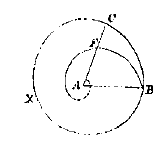 Stel dat de spiraal AFB beschreven is in de cirkel BCX, zodanig dat er altijd dezelfde verhouding is van de omtrek BCX tot de boog BC, als van AB tot FC, of van het kwadraat van AB tot het kwadraat van FC, of van de derde macht van AB tot de derde macht van FC, ofwel van welke macht van AB men wil tot de zelfde macht van FC: te geven de algemene regel om de verhouding te vinden van de cirkel BCX tot de ruimte omvat door de rechte AB en deze spiraal AFB, van welke macht deze ook kan zijn.
Stel dat de spiraal AFB beschreven is in de cirkel BCX, zodanig dat er altijd dezelfde verhouding is van de omtrek BCX tot de boog BC, als van AB tot FC, of van het kwadraat van AB tot het kwadraat van FC, of van de derde macht van AB tot de derde macht van FC, ofwel van welke macht van AB men wil tot de zelfde macht van FC: te geven de algemene regel om de verhouding te vinden van de cirkel BCX tot de ruimte omvat door de rechte AB en deze spiraal AFB, van welke macht deze ook kan zijn.