Lengte , maat , landmeten , drieroe , zichtlijnen , berekening , Oppervlakte , Volume , Noten
Stevins Meetdaet2 - MetenIn het tweede boek van de Meetdaet komt het eigenlijke meten aan de orde. Stevin geeft geen definitie van dit woord 'meten'. In het Cortbegryp staat over de eerste twee boeken: eerst beschrijven der grootheden Maecksel of teyckening.Hoeveel er in begrepen is. We moeten wel bedenken dat 'grootheyt' betekende: grootte, en niet ons woord grootheid. Het ging meestal om de afmetingen van iets concreets, om lengte, breedte, hoogte, oppervlakte en volume. Wij kunnen het hebben over de grootte van een gewicht, maar bij Stevin is wegen iets anders dan meten. Wegen is het bepalen van een 'swaerheyt' (zwaarte), en dat is een onderwerp uit de Weegkunde. 1 De 'grootheyt' is het onderwerp van de Meetkunde, zoals het 'ghetal' dat is van de Rekenkunde. De Meetdaet {Praxis Geometriæ.} hoort bij de meetkunde. Lengte1. "deur overgheleyde maet", met een maat die wordt afgepast, 2. "deur sichtstralen", met driehoeksmeting, 3. "deur ander bystaende bekende linien", zoals een loodlijn of middellijn. Alleen de eerste voldoet aan de hedendaagse strikte definitie van meten: het vergelijken van een grootheid (hier: lengte) met een eenheid, door middel van een meetinstrument. Bij de tweede en derde manier zijn berekeningen nodig. De tweede speelt een belangrijke rol bij de landmeting, het probleem waaruit de meetkunde (geometrie) ontstaan is. MaatBij het meten is een eenheid nodig, een standaard-maat, en een schaalverdeling. Op oude landkaarten staan meestal enkele staafjes van de onderstaande vorm, voor de verschillende mijlen die in gebruik waren. Zo'n schaalverdeling lijkt op een 'leer' of ladder (Latijn: scalae) met zijn traptreden. 2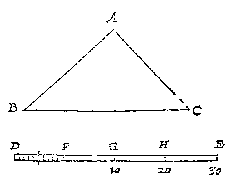
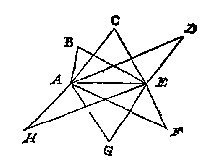
Laet AB, BC, CA, drie linien des driehoucx ABC wesen, ende DE een leer: Om welcx ghedaente met een te verclaren, soo is te weten inde ghebruyck te sijn, by de ghene die metselrijen, timmeragien, sterckten, landtcaerten, zeecaerten, en dierghelijcke teyckenen, daer benevens een maet te stellen als de voorschreven DE, die om haer lijckformicheydt met een leer, oock leer ghenoemt wort, ende als haer ghedeelten niet seker voeten, roeden, mijlen, of dierghelijcke en beteyckenen, soo heetmense int ghemeen, oock om de lijckformicheyts wil, trappen.En dan volgt ook nog een voorbeeld: 20 + 4 = 24. En zo doe je het ook met de andere lijnstukken. Tot in de kleinste details legt Stevin het uit, zodat iedereen het snapt, ook wie nog nooit een meting heeft meegemaakt. Dit is weer een punt waarbij Stevin het decimale stelsel kan aanprijzen: op dat wy noch wat bequaems daer in verclaren, soo is te weten dat sijn V O R S T E L I C K E G H E N A D E , om int meten der linien en platten op papier, oock der lichamen int cleen deur de thiende te wercken, dat is deur heele getalen sonder ghebrokens, heeft inde ghebruyck de langden als FG, GH, HE, beginselen te noemen, dat sijn (0), sulcx dat FE doet 3 beginselen, ende de deelen DF eersten, als (I)De 'beginselen' zijn dan wat wij de eenheden noemen, en de 'eersten' tienden. Ende soo de passer int meten opt middel tusschen twee punten valt, voor dien helft worden 5 (2) gherekent; Maer soo t'ghesicht can oirdelen opt derdendeel van 1 (I), men schrijft daer voor 3 (2), of 4 (2) [...]Stevin geeft aan haar, dat is aan zijne V. G., steeds alle eer die haar toekomt op het gebied van wiskundige vondsten en toepassingen. Hier lijkt hij de glunderend toekijkende leraar die blij is dat zijn hooggeboren pupil het goed doet, en er bovendien plezier in heeft. Maurits was bijna twintig jaar jonger dan Stevin, maar hij was toch al 26 toen in 1593 het intensieve contact tussen beiden begon. Bij de vele verwijzingen naar wiskundige activiteiten van zijne V. G. staat helaas niet wanneer die plaats vonden. In 'Vande Vernieuwing des Wysentijts' (lidt 4) is er wel sprake van gemor over tijdverspilling, "int middel van een regiering diens mare [...] rontom den Eertcloot loopt". LandmetenHoe meet je grote afstanden een beetje nauwkeurig? Voorbeeld 2 zegt: met een ketting. Die rekt niet uit, is niet al te zwaar, en kan makkelijk opgeborgen worden. Ringen en ogen moeten wel goed vast gesoldeerd worden:Tis by veel Landtmeters inde ghebruyck een keten te hebben van yserdraet, of coperdraet [...] ghemeenelick lanck vijf roeden. |
Angaende de roe die is in Hollant van 12 voeten, en elcke voet van 12 duym, waer af de drie dats een vierendeel voets Rijnlantsche maet sijn van dese langde |
|
Een kwart Rijnlandse voet staat afgetekend in het boek: een streep van 7,9 cm lengte. Een roe was 3,77 m, de 'keten' van vijf roeden bijna 19 m. 3 Om met de ketting een afstand te meten: gaet de meter mettet een eynde des ketens voor, ende doende hem een ander navolghen mettet ander eynde, steeckt alsoo op elcke langde des ketens, tamelick ghespannen staende, een stocxken, of pinne, lanck ontrent een voet, of soo veel langher alst de noot vereyscht, van weghen lanck cruyt, ghewas, of dierghelijcke DrieroeHet meten van grote afstanden kan ook anders: met 'zichtstralen'. Op blz 49:W A N T E R een ghemeene wijse van meting is sonder te moeten overgaen de wech daermen de langde af begheert te weten, namelick deur sichtstralen, welcke langden met een ghebruyckelick woort ongherakelicke langden ghenoemt worden, soo sullen wy vande selve wat segghen.Een onbereikbare lengte wordt bekend met driehoeksmeting: Daer sijn tot desen handel bereyt ettelicke wisconsttuyghen {Instrumenta mathematica.}, wiens namen wel verscheyden sijn, als Platmeter, Hoochmetingsleer, Meetconstich viercant met een sichtregel, Meetconstich viercant met een hangsnoer, Meetstrael, Almeter, Drieroe {... Triquetrum.}, ende meer ander.Een 'leer' is een ladder of schaalverdeling. De 'Hoochmetingsleer' {Scala altimetra} is misschien de jacobsstaf (kruisstaf, graadboog, graadstok) die op schepen gebruikt werd: een stok met een verschuifbare dwarsstok en een schaalverdeling. 4 Doch makense altemael driehoucken, welcke deur een of meer beweghende sijden verscheydelick verandert worden lijckformich metten grooten meetbaren driehouck, sulcx dattet ghebruyck vant een wel verstaen sijnde, ghenouchsaem kennis van allen gheeft. Twelck aenghemerckt wy sullen hier inde plaets van velen de drieroe verkiesen:Dan volgt een vrij uitvoerige beschrijving van de "ghedaente der drieroe": 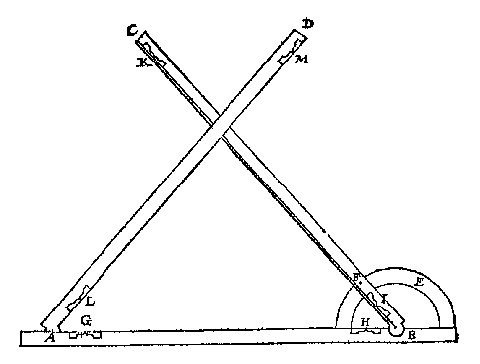
drie roen, waer af den tuych oock soo bequamelick op duytsch schijnt drieroe te meugen heeten, alsmen een stoel van weghen haer drie voeten drievoet noemt [...]Streepjes op minder dan een mm afstand! De drieroe komt met 'clemhaecken' op een "viercant bart breet ontrent een voet, ghehecht op een stock ghelijck de plaet vant meterscruys". De roen [...] en laetmen niet mette vijle bereyden, maer men doetse deur een schrijnwercker schaven [..] want hem t'lattoen tottet schaven wel ghevought.Messing heet in het Frans: laiton. Om nu wat vande stof te segghen, lattoen wort voor veel meetconstighe tuyghen de bequaemste gheacht, want hoewel goudt schoonder is daer teghen ist weycker ende cromt haest. Boven dien eenich tuych van goudt of silver wel gemaeckt sijnde, t'staet in perikel van by noot ghebroken te worden om sich daer mede te behelpenBedoeld zal zijn: financieel behelpen, verkopen van een onderdeel van het instrument. Yser verroest: Loot en tin sijn te sacht: Angaende hout t'is onbequaem voor dinghen die recht ende in standt moeten blijven, deur dient inde sonne crom ghetrocken wort, oock in vochtich weer opswelt, ende sommighe deelen die schuyven of draeyen moeten soo stijf doet clemmen, datmense qualick van een can crijghen, die ter contrari in drooch weer van selfs uyt malcander vallen:Het beste materiaal is messing, te meer datment voor de ghene die t'cyraet begheeren met cleene cost schoon vergulden mach.Waar kun je een 'welgemaeckte' drieroe kopen? En wat kost die ongeveer? Deze vragen werden aan Stevin gesteld door een organist, aan het eind van een brief over de 'Singconst'. ZichtlijnenVoorstel 2 gaat over het gebruik van de drieroe bij het met zichtlijnen meten van een "onghenakelicke" horizontale lengte. Er zijn twee standplaatsen nodig, op bekende afstand. Stap voor stap legt Stevin uit hoe het in zijn werk gaat, met drie voorbeelden.De "regel van drie" voor evenredigheid wordt weer toegepast, zoals: Ick segh CE 100 (0), gheeft CF 80 (0), wat CB 150 roen ? comt voor CA 120 roen.Ook zijn er enkele praktische opmerkingen: - het kan zonder berekenen door de linkerroe te verschuiven naar een handig getal, - als de uiteinden elkaar niet raken moet je de linkerroe verschuiven, - beter niet de gemeten hoek 'bewaren' op de drieroe, maar aflezen. Dit laatste omdat de tweede standplaats altijd op voldoend grote afstand van de eerste moet zijn. De rechterroe kon met een schroef vastgezet worden, maar dat is niet aan te raden bij: standen die verrer van malcander ligghen als drie of vier uyren gaens, ghelijckt int teyckenen van landtcaerten ghebeurt, alwaert moeyelick mocht vallen dien houck sonder veranderen soo wijt te brenghen [ 5]De hoogte van een toren meten kan ook met de drieroe (blz 57). Een schietlood of 'lootsnoer' is dan nodig voor het vertikaal stellen, en het heeft nog een andere functie: 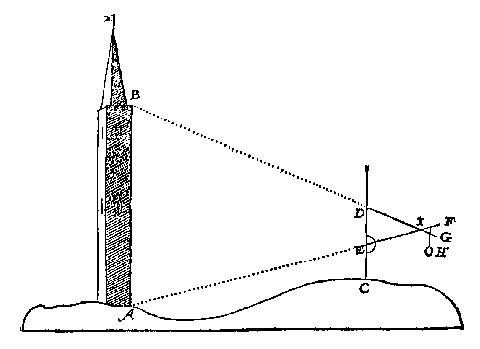
op dat de selve roe DG t'elcken blijve staende daermense set, soo isser ant eynde van dien een lootsnoer als H, alsoo dattet met een keer over de rechterroe te gheven, de slinckerroe in sulcken plaets houdt alsmense stelt.De afstand tot de voet van de toren is niet altijd makkelijk te bepalen: ick meet de langde van I tot A met een maet, als keten of roe soo icker commen can, maer canmen om eenich belet van wateren, huysen, vyanden, of dierghelijcke, de langde van I tot A alsoo niet meten, men salse vinden deur een tweede standt, na de leering des 2 voorstelsVijanden kunnen op allerlei manieren lastig zijn! Op blz 59 geeft Stevin nog "een ander lichter manier" met een tweede meting. Theoretisch is er nog een probleempje: Anghesien AB ende ED beyde rechthouckich op den sichteinder sijn, soo wordense in sulcke werckelicke voorbeelden voor evewijdeghe ghehoudenMaar in de bewerking kan dat verwaarloosd worden. Een andere hoogtemeting is die van dijken en wallen (blz 61): T'ghebeurt dickwils in bedijckte landen, oock in sterckten, dattet noodich is de hooghde der dijcken wallen en bolwercken te weten, soo wel in haer gedeurich onderhoudt, als int opnemen wanneerse eerst ghemaeckt sijn. |
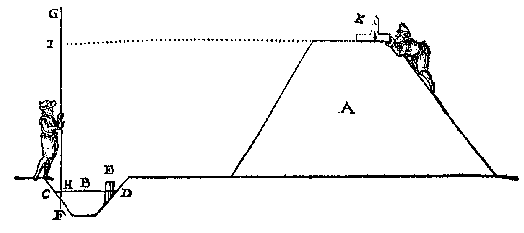
Die handige Hollanders:
stellende an I een kerf, ende eenich sichtbaer teycken daer op, als een ghewronghen neusdouck daer an ghecnocht gelijck een rinck diemen hooger en leegher verschuyven mach [...]Maar zijne V. G. heeft met deze laatste manier een voorbeeld "seer nauwe berekent", en gevonden dat deze niet goed is op grote hoogte, en bij grote afstanden. BerekeningDe derde manier om een lijnstuk te meten (na afpassen en driehoeksmeten) was: "door bystaende bekende linien". Daarvoor is eerst nog wat theorie nodig, over het berekenen van een loodlijn: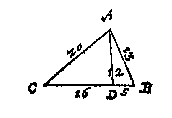
want ons int meten met twee standen seker ses linien ontmoeten, waer af men deur vijf bekende vindt de seste onbekende, soo sullen wy daer af segghen int 5 voorstel, eerst beschrijvende het 4 voorstel daer toe noodich vant vinden der hanghende, en haer twee hangendens grondenGegeven een driehoek ABC met loodlijn AD, en AB = 13, BC = 21, AC = 20. Hoe bereken je AD, BD, en DC? Stevin lost dit probleem op met stelling 13 uit boek 2 van Euclides (vergelijk de cosinusregel): de kwadraten van AB en BC zijn samen het kwadraat van AC plus 2 x BC x BD. Er stond wel de opmerking dat dit soort berekeningen "in haer besluyt deur wortelen {Numeros radicales.} heel volcommen connen sijn" (anders dan die in het boek 'Driehouckhandel', met de sinustabel). Maar toch geeft Stevin een voorbeeld van een zesde onbekende die te vinden is met hele getallen. 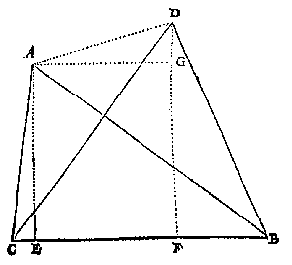 De basislijn BC is gemeten door afpassen, de twee driehoeken daarop zijn gevonden door metingen met de drieroe. Het is echt een probleem voor de liefhebber, heel ingenieus geconstrueerd met rechthoekige driehoeken (3, 4, 5 en zo meer): BC = 1400, AB = 1615, AC = 975, DC = 1500, DB = 1300. Bereken AD.
Hier uyt is kennelick dat by aldien de punten B, C, D, F, G, H, beteyckenden Steden, dorpen, of torens, die op de twee standen A, E, uyt het landt aldus op papier caertschewijse ghebrocht waren, hoemen soude vinden deur ghetalen de langde van d'een tot d'ander. BijlEen vierhoek met twee evenwijdige zijden heeft enkele eigenschappen die handig zijn bij berekeningen. Zo'n vierhoek noemen wij een 'trapezium' (van het Griekse tetra-peza - viervoet), maar omstreeks 1600 was de Latijnse naam 'mensa' (tafel) in gebruik. Stevin weet een betere (voorstel 6):dat bijl hier ghenomen wort t'ghene by de Latinen mensa heet, om dat de vierhouck met twee evewijdeghe ende twee onevewijdeghe sijden (ansiende bijlen en tafels soomense nu gemeenelick maeckt) beter een bijl dan een tafel gelijckt. PiNa een voorbeeld-berekening met een regelmatige veelhoek komt voorstel 8:Deur de bekende middellijn des rondts den omtreck te vinden.De cirkelomtrek kan gemeten worden met afpassen van een maat, als die maar klein genoeg is: Soomen desen booch wilde meten met opgheleyde maet, men soude die soo cleen meughen nemen dat de langde der selve, verleken by den booch daer mede overcommende, gheen merckelick verschil en hadde: [...]Dacht Stevin echt dat pi ooit wel eens helemaal gevonden zou kunnen worden? Hij zegt zelf: Daer benevens soo isser voor de ghene die nauwer rekening begheeren een oneyndelicke naerdering bekent, sulcx dattet verschil vant ware, cleender sal sijn dan eenich gheeynt ghetal hoe cleen het is.Bij een oneindige reeks is "alsnoch niet" een beetje komisch (ook op blz 173: "alsnoch onbekent"). Maar het was toen nog niet duidelijk of zo'n benadering een echt getal kon opleveren, en of het niet een of ander wortelgetal was. Stevin geeft de indrukwekkende prestaties van de hooggeleerde Adrianus Romanus en Meester Ludolf van Ceulen: pi met 17 resp. 21 significante cijfers, welcke voorschreven rekeninghen sy ghemaeckt hebben sonder d'een van d'ander te weten.In de praktijk wordt 22/7 gebruikt, ook voor de oppervlakte (voorstel 12). OppervlakteHet gaat hierbij natuurlijk om berekeningen, te beginnen met de driehoek: Ick meet eenighe sijde als BC, bevinde die neem ick van 8, en treck AD hanghende op de selve BC die ick bevinde van 6, welcke gemenichvuldicht deur 4 helft van CB, comt voor t'begheerde plat 24Oppervlakte is halve basis maal hoogte, zie Euclides (41 voorstel des I boucx). Doch machmen oock andersins den helft der hanghende dats 3, menichvuldighen deur den heelen gront 8, en comt oock 24. Oft andersins segghen 6 mael 8 is 48, diens helft alsvooren 24. Ende mach sulcken helft bequamelicxt ghenomen worden van die lini der twee diens ghetal parich is, om wercking int ghebroken te schuwen.Kies zo mogelijk een even getal, dan krijg je geen breuk. Elke veelhoek kan opgedeeld worden in driehoeken, en als de diagonalen gemeten kunnen worden is de oppervlakte te vinden. Maar soms is er een probleem (voorbeeld 4): T'ghebeurt int dadelick lantmeten, datmen de langden van ettelicke linien diemen behouft int rekenen [...] niet meten en can, deur belet van water, huysen, of dierghelijcke, doch dat eenighe ander linien wel connen ghemeten worden, maer t'werck moet deur rekening der platte driehoucken afgheveerdicht sijn, daer af wy nu segghen sullen, stellende een voorbeelt dat sijn V O R S T E L I C K E G H E N A D E gheteyckent[,] seer nauwe ghemeten en berekent heeftHet gaat om een vijfhoek waarvan alleen de zijden bekend zijn en een hoek met zijn drie delen. Hier moet de sinustabel weer gebruikt worden. Ook een andere verdeling dan die in driehoeken kan handig zijn (vb 5): deyling in bijlen comt dickwils te pas om landen in seker cavels te deelen, diemen met evewijdeghe linien begheert te scheyden. Maer hoemen die cavels alsoo elck van begheerde grootheyt crijcht, sal t'sijnder plaets int 11 [14] voorstel des 5 boucx vande Everedentlicke snyding der grootheden verclaert worden. KromDan komen de kromlijnige vlakken: cirkel, ellips, stuk van een parabool, en van een spiraal, boloppervlak.Stevin maakt nieuwe woorden voor: cirkelsector en -segment (voorstel 13): Daer gheschien int rondt twee besonder vermaerde sneen, d'eene met twee halfmiddellijnen, wiens deel ick halfmiddellijndeel noem, d'ander met een peez ick peezdeel heete: 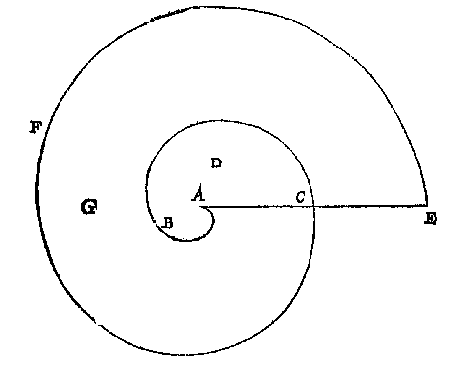 Bij de spiraal kunnen we ons afvragen of Stevin met opzet de ingesloten vormen genoemd heeft: D en G. Ze lijken op hun naam!
Bij de spiraal kunnen we ons afvragen of Stevin met opzet de ingesloten vormen genoemd heeft: D en G. Ze lijken op hun naam!
Te meten een ghegheven slangtreckplat, bestaende uyt een of meer heele keeren. We zien weer de verbluffende prestaties van Archimedes: ook een gekromd boloppervlak kon hij berekenen (verwijzingen bij voorstel 18 en 19). Wie kan tegenwoordig nog een manier vinden, zonder integraalrekening, voor: "het bultich vlack eens clootdeels, dat met een plat vanden heelen cloot ghesneen is"? Mij verraste al de uitkomst van het probleem: van een half boloppervlak een 'riem' af te snijden met een zelfde oppervlak als de rest. Het berekenen van cilinder- en kegelvlakken hoeft Stevin niet apart te behandelen, voor elk geeft hij kort en duidelijk de methode aan. Wel wijst hij nog op een vondst van Archimedes: met een middelevenredige is een cirkel te vinden met een zelfde oppervlak (blz 84). LandTenslotte een belangrijke praktische toepassing van oppervlaktemeting (voorstel 20):Wy hebben tot hier toe beschreven het meten der vlacken, dienende int ghemeen tot vlacken van alle stoffen [...]De eenheden kunnen verwarrend zijn. Als voorbeeld is er een driehoekig stuk land, waarvoor: comt 3395 roen 5 (I) 6 (2): Nu gherekent na de hollantsche wijse 600 roen op de morghen, soo is dien driehouck groot 5 morgen 395 roen. 5 (I) 6 (2).600 vierkante roeden = 600 x 3,772 m2 = 0,85 hectare. Niet iedereen is al toe aan decimale breuken: soomen de 5 (I) 6 (2) deur voeten en duymen wilde uytspreken na landts ghebruyck, men siet op de roe wat daer me overcomt, en moet sijn 6 voet 8 16/25 duym.Op blz 49 stond dat de 'roe', dat is nu de meetlat, verdeeld is in 12 voeten (elk van 12 duim), en ook "op een ander sijde noch ghedeelt in 10 even deelen die wy eersten noemen en elcke eerste andermael in thien, t'welck tweeden sijn". 0,5 roede = 6 voet, en 0,06 roede = 8 16/25 duim (0,06 x 144). Maar het was toch een oppervlakte, en geen lengte? Op p. 85: Doch staet hier te mercken dat de boveschreven 6 voeten 8 16/25 duym, niet en sijn 6 viercante voeten, en 8 viercante duymen, maer tis een rijem landts lanck een roe, breet 6 voet 8 16/25 duym [...]Een riemvoet is dus een strook van een roede bij een voet. Hoe gaat de meting bij onregelmatige vormen? Om landen te meten begrepen in ongheschickte cromme linien, ghelijck inde lantmeting dickwils te vooren commen, men stelt soo veel baecken inden omtreck, tot dat de cromte tusschen twee baecken begrepen, gheen hinderlick verschil by en brengt, daer na meetmen die form als een rechtlinich plat met soo veel houcken alsser baecken staen [...]En in bergachtig land? 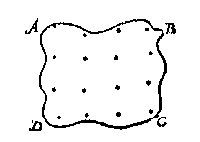
Laet ABCD beteyckenen den omtreck des voets of gronts van een berch: Nu want het verheven bultich vlack des selven berchs op dien grondt staende, een ander en grooter is dan t'plat begrepen in een omtreck als ABCD, soo moet hier een ander meting toe gebruyckt worden, t'welck geschien mach met op den berch te steken verscheyden baken, welcke hier beteyckent worden mette tippelinghen daer in vervanghen, diemen soo na of verre van malcander stelt als de saeck vereyschtOver de meetnauwkeurigheid heeft Stevin ook iets op te merken (blz 86): datmen int meten met groote moeyte seer nau gaslaet, dinghen die soo grooten sekerheyt niet en behouven: En weerom verkeert, datmen ettelicke dinghen niet seer nau en meet, die nochtans nauwer maet vereysschen [...]Als voorbeeld neemt hij een strook land, lang 800 voeten, breed 10 voeten: Ghenomen nu datter op de langste sijde [...] int meten een voet ghemist wierde,Dan zou dit niet zoveel uitmaken als wanneer op de kortste zijde een voet gemist werd! In de Driehouckhandel staat ook zo'n voorbeeld met een "platte rechthouck" (blz 149). Zijn Vorstelijke Genade heeft nog een praktische regel bedacht: het oppervlak is evenredig met het kwadraat van een zijde. Daarmee kun je: t'begrijp des landts noch vinden sonder landt te meten, of immer deur t'meten van alleenelick een lini, treckende de form des landts tusschen seker palen begrepen op papierDus: werk op papier, met een zijde en de vorm van het stuk land. Je hoeft niet zo ver te lopen als je een kaart hebt! Stevin kan de regel wel bewijzen, met hulp van Euclides. Tis wel waer dat sulcke wercking meerder sekerheyt heeft uyt het groot int cleen, dan uyt het cleen int groot [...] VolumeToepassingen worden genoemd: Een dijck of wal wiens meting inde bedijckte landen en sterckten genouch te vooren comt, wort int meten aengesien voor een liggende pylaer, diens gront een bijl isEen "plattich lichaem van form soot valt" wordt verdeeld in piramides, zoals rechtlijnige 'platten' in driehoeken. Maak je eigen meetinstrument, een staande liniaal: Men sal hebben van stof daer toe bequaem, een cruys [...] ende een rije [..] rechthouckich opt selve cruys [...]Ook wordt behandeld een geval met een "onsienlicken gront" die in driehoeken verdeeld moet worden. Zulke metingen kunnen best lastig zijn: Maer om int meten niet te dolen, te weten datmen t'ghemeen soppunt altijt kenne, ende t'een voor t'ander niet en neem, oock datmen de meetbaer ende onmeetbaer platten wel onderscheyde, soo salmen ten eersten t'ghemeene soppunt een teycken gheven, met crijt of inckt, na gheleghentheytStevin heeft kennelijk geen andere beschrijving van deze meetmethode gevonden: In dese manier der meting van ongheschickte plattighe lichamen, die ick meen nieu te wesen, heeft sijn V O R S T E L I C K E G H E N A D E metter daet heur gheoeffent, ende bequaem bevonden.Nu zou kunnen volgen: het volume is evenredig met de derde macht van een zijde. Deze regel wordt hier niet genoemd, maar wel toegepast in boek 3. Boek 2 besluit met de bol, de ellipsoïde, en de paraboloïde.
Noten |