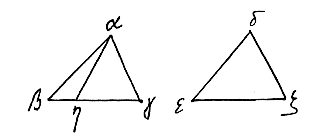
Basson , Bacon , Porta , Theon , syllogisme , fluit
BewegingOf er een kleinste beweging is. *)Basson, in het boek Over Beweging°), meent dat een er kleinste beweging bestaat, en ongetwijfeld zal hij ook menen dat er een kleinste tijd is. Maar wie kan met het verstand begrijpen dat één atoom niet zijn plaats kan veranderen tenzij geheel, dat wil zeggen dat het niet kan gebeuren dat het niet geheel zijn vorige plaats opgegeven heeft, en gedeeltelijk buiten zijn eerdere plaats uitsteekt? En ook houdt een oneindige verdeling niet in dat een atoom in een eindige tijd geen enkele lengte, hoe klein ook, kan doorlopen, omdat ook een eindige tijd in oneindig kleine tijden verdeeld kan worden. Wat is er dus wonderbaarlijk aan, als een atoom zo'n lengte in zo'n tijd doorloopt? [<] Maar ik, terwijl ik stel dat er atomen zijn, stel me die niet zo voor dat ik ze niet in gedachten kan verdelen, maar zo dat ze, daar ze poriën missen, in werkelijkheid niet verdeeld kunnen worden. Verdeling in gedachten bracht Aristoteles ertoe een willekeurig deeltje tot in het oneindige te snijden; de vaststelling van atomen bracht Basson ertoe zodanige atomen te beschrijven die in gedachten niet verder verdeeld kunnen worden, dat de menselijke geest ze niet kan vatten.
[ *) Afbeelding in Beeckmans handschrift.] °) In het werk aangehaald op p. 243 hiervoor (Philosophiae naturalis adversus Aristotelem Libri XII, Gen. 1621, Amst. 1649), 'Liber de Motu', Intentio VII, Art. 3, p. 406 [1649, p. 365] en Art. 4, p. 410 [1649, p. 369]. |
|
Een punt is dan niet een atoom van een lichaam, en beweging is niet te verdelen tot op de kleinste beweging, en ruimte niet tot op de kleinste ruimte, en tijd niet tot op de kleinste tijd. Uit momenten ontstaat immers geen tijd volgens de Peripatetici, want tussen twee willekeurige momenten is er tijd. En ook al kan ik niet goed verklaren wat tijd eigenlijk is, en hoe de voortgang is tussen twee afzonderlijke momenten, dit kan toch niet wonderlijker schijnen dan het uitstrekken van de ruimte tot in oneindige, of eeuwigheid van de tijd, of uitgestrektheid van lichamen tot in het onmetelijke, of de inwendige natuur van atomen, die we lichaam noemen.
Terecht zeiden dus de Ouden: God schiep alles met gewicht, tijd en maat. Wat dat gewicht is, wat het wezen is van tijd, en wat de continuïteit van ruimte, schijnt al ons begrip te boven te gaan. Gewicht hebben ze lichamelijkheid genoemd, en maat een of andere ruimte; en uit een atoom van ruimte en tijd onstaat alle gelijkmatigheid van beweging en afwisseling ervan alleen volgens rustpunten. [ Afbeelding van Beeckmans handschrift.] Kleine en grote vlamOf een kleinere vlam wordt gedoofd door een grotere.Basson, Lib. de Actione, pag. 448, zegt dat een kleinere vlam wordt uitgedoofd door een grotere, omdat de grotere, strevend naar meer ruimte, de kleinere samendrukt, dat wil zeggen plaats ontneemt waarin hij zich zou kunnen uitbreiden. [<]
Maar als dit waar zou zijn, zou een brandende kaars in een omgekeerd glas op een wateroppevlak, het water niet aantrekken maar, naar meer ruimte strevend, het water veeleer neerdrukken en wat lucht uitdrijven door het water heen. De reden hiervan heb ik hiervoor*) geplaatst in een toeneming van vacuüm, als de vlam lucht wegneemt door de poriën van het glas, en dat zo het water wordt weggedrukt naar lege plaatsen, en dat de vlam uitgaat door gebrek aan lucht en samendringing. *) Zie T. 1, p. 39 ["de locht, verdunt synde, vliecht door het glas wech"] en T. 2, p. 195 en 228 [hete lucht niet door glas]. [ °) Zie Basson, 1621, p. 333 (1649, p. 300), Lib. 'De Natura', Intentio III: 'De anima mundi', Art. I: "Wat die substantie is die bij verdunning in vuur gaat en in lucht, en andere lichamen".] 's Ochtends kouder dan te middernachtWaarom het 's ochtends kouder is dan midden in de nacht.En op pag. 466, wanneer hij vraagt waarom het 's ochtends kouder is dan midden in de nacht, is het niet noodzakelijk dat koude lichaampjes dooe de stralen van de Zon naar ons worden geduwd, ofschoon hier ook iets waars in zit, vooral als hij die koude lichaampjes vuurdeeltjes ontberend noemt, en dat de stralen van de Zon de koude lichaampjes niet samendrukken, maar voortstuwen als ze die met hun beweging raken. Maar toch zou het volstaan te zeggen dat de vuurdeeltjes, die in de lucht verborgen zijn, midden in de nacht nog niet allemaal zijn uitgewasemd, en dat er in de ochtend dichtbij de Aarde nog meer uitgaan dan de weinige stralen van de Zon er naartoe kunnen brengen. |
En op pag. 470: ik had liever gezegd dat samendrukking door koude ontstaat wanneer er lichaampjes aanwezig zijn die weinig vuur in zich hebben, of als vuur door samendrukking uit een lichaam gaat, of als er een koud lichaam bij komt. Deze koude lichamen namelijk nemen, daar ze koud zijn, vuur weg uit het lichaam door het samen te drukken, in de plaats waarvan de leunende lucht enz. de dichtst bijzijnde lichaampjes duwt. En in een levend wezen trekt het gevoel ook op een andere manier geesten [spiritûs] naar binnen. Vis in samengeperst waterOf een vis kan leven in samengeperst water.Ik vraag me opeens af, of een vis in water, dan wel een muis in lucht, als het vat waarin deze dieren zijn aan alle kanten met heel veel geweld is samengeperst, kunnen leven, of dat deze samenpersing zo bij hen zal aankomen, dat de vrijheid zou worden ontnomen aan de muis om te ademen, en aan de vis om water aan te trekken, en elk vermogen om zich te bewegen, daar noch het water, noch de lucht, meer kan wijken dan ze al hebben gedaan. Als ze zich nog bewegen, moet gezegd worden dat met water en lucht hetzelfde gebeurt, als met stenen bolletjes die in een vat zijn samengeperst. Want ook al drukt het vat daar geweldig op, er worden toch overal enige bollen gevonden die vrij zijn van de samenpersing, die nog enigszins vrij kunnen bewegen, daar immers andere samengeperste bolletjes er omheen enige lege ruimte in stand houden, als het ware een boog vormend. Slotsom over BassonWat voor iemand Basson is.Overigens, zoals deze Basson veel heeft dat goed is, zo heeft hiij ook het een en ander dat verkeerd is. En hij zou de mening van Democritus niet zo slecht hebben bestreden, op pag. 578 enz., als hij de aard van kijkerbuizen en brandspiegels wiskundig voldoende gekend zou hebben, zoals Kepler [<]. Maar ik zie ervan af tegen hem te betogen, aangezien mijn mening duidelijk genoeg blijkt in het vorige van dit boek, met slechts deze kanttekening, dat ik bij deze gelegenheid iets nieuws ben tegengekomen. StemLengte, breedte en diepte van een stem.Dat een stem bij het spreken verandert is het meest kenbaar aan scherpte en zwaarte, snelheid en traagheid, volheid en zwakte. Wat genoemd kan worden de lengte, breedte en diepte van de stem. Zo is de mate van verbazing, wanhoop, verontwaardiging, vreugde, bezwering, medelijden, afschuw en verwensing, ondervraging enz. niet alleen te halen uit de scherpte en de zwaarte, zoals misschien gezien zou kunnen worden bij sommigen die met nadruk spreken, maar vooral uit de volheid en de traagheid en de verschillende manieren daarvan. Stem en handenVollere stem bij neerlaten van een hand dan bij opheffing.Merk ook op dat bij slagen van de hand, wanneer we zingen, de stem bij het neerlaten van de hand voller is dan bij het opheffen, en weer voller in het begin van het opheffen dan aan het eind. Waaruit voor ervaren musici bekend wordt de eerste, tweede, derde enz. noot bij de slagen; ja zelfs leken in de muziek die het gezang alleen horen, volgen dezelfde beweging met lichaam en geest. Wat we eerder [<] bij het verschil van de pauzes misschien ook niet slecht hebben verteld. Laten we dus moeite doen, als we elk affect met de stem willen uitdrukken, om te weten in welke afwisseling van de ene of de andere lettergreep elk affect volgens de genoemde manieren naar zijn aard gelegen is, wat betreft de stem. |
Vallende druppelsWaarom er een overblijfsel opstijgt als druppels vallen.Francis Bacon, heer van Verulam, zegt in Lib. 2 van Novum Organum, Aforisme XXV*), dat wanneer druppels gevallen zijn, een overblijfsel zich samentrekt en opstijgt.
Waarvan veeleer te menen is dat het gebeurt wegens een gelijkmatige samenpersing van de lucht, waarmee ik hiervoor [<] heb laten zien dat alles wat gemakkelijk meegeeft wordt samengeperst tot bolletjes, toen ik het had over het terugspringen en de samenpersing van de kleinste 'homogenea'. *) Francis Bacon, Instauratio Magna, Lib. 2: Novum Organum, sive Indicia vera de Interpretatione naturae, p. 227-228 (Londen 1620). [Bacon, p. 228: kasteel van zeepbellen blazen.] [ Engl.; Ned. vert. Willem Visser, Amst. 2016. Ander werk van Bacon hierna: p. 276, 327, 330, III, 51. Alberto Elena, 'Baconianism in the Seventeenth-century Netherlands', Nuncius 1991, fasc. 1, 33-47.] |
KleurenReden van kleuren, waarom ze zo zijn.Evenzo zegt hij ook, op pag. 224, dat lichamen die helemaal effen zijn (wat betreft delen die het zien beïnvloeden) het doorschijnende geven; maar dat oneffen lichamen met een enkelvoudige textuur, wit geven; dat oneffen lichamen volgens een samengestelde textuur, maar geordend, de overige kleuren geven, behalve zwart; en dat oneffen lichamen met een samengestelde textuur, maar helemaal ongeordend en verward, zwart geven.
Hij bedoelt misschien dat een geordende textuur muzikale verhoudingen met zich meebrengt, zodat de witte kleur in verband staat met het octaaf, namelijk met twee lichamen waarvan het ene tweemaal zo groot is als het andere. Dan zal een wit lichaam bestaan uit twee soorten lichaampjes, gelijk in aantal, maar verschillend van grootte op de genoemde manier.
Hij verschilt dus niet van mij wanneer hij denkt dat kleuren voortkomen uit een verschillende ligging van de deeltjes, maar hij schijnt verschillen van de afzonderlijke verder te hebben opgespoord. Maar wat hij meent over de daardoor weerkaatste lichtstralen, laat hij niet zien. Tot Middelborgh, int laetste van Julius. *) Over kleuren als consonanten: Combarieu, La musique, ses lois, son évolution (Parijs 1920), p. 278-279. [T. 4, p. 348 (Additions). Cf. Aristoteles, lib. 'de sensu & sensili' cap. 3; Engl.] [>] Luchtbel
*) Dit had Bacon gezegd op p. 256 [Lib. 2, Afor. 35]. °) De druk omhoog [>], de 'anôsis' van Aristoteles. [ Modern Grieks: 'anôsè' - opwaartse kracht van Archimedes. Motus plagae - beweging van een slag. Bacon, p. 312 (deel 2, Afor. 48) noemt Democritus en 'motus plagae', volgens hem is dit niet anders dan een 'motus libertatis'. Zie ed. Th. Fowler, Oxf. 1889, p. 461, 536.] Fouten van BaconFouten van Verulam.Franciscus van Verulam, pag. 263, concludeert verkeerd dat de dagelijkse beweging aan de hemel is, met verschijnselen die zich ook zouden vertonen bij een bewegende Aarde. Want omdat ze sneller met de Aarde naar het Oosten bewegen, zou het dan een wonder zijn als ze langzamer naar het Westen lijken te gaan, zowel water als lucht, en kometen, en planeten (die hij als voorbeelden aanvoert)? |
|
Van dezelfde aard is dat hij zegt dat de beweging van een steen in lucht wordt voortgezet door terugvering van inwendige delen, en dat het midden van een kaarsvlam precies hetzelfde blijft.*)
Dezelfde, pag. 284, vergist zich misschien, wanneer hij zegt dat gewicht overeenkomet met hoeveelheid materie. *) Cf. o.c., p. 269, resp. 272. WijngeestWijngeest en zijn verhouding tot damp.Dezelfde, pag. 286, heeft gevonden met een blaas, vastgebonden aan een flesje, dat damp van wijngeest honderd maal zoveel ruimte inneemt als wijngeest zelf, want hij heeft damp van wijngeest opgevangen in een blaas, waarvan hij de inhoud wist. Hij zegt ook dat wijngeest 21 delen ruimte inneemt, waarvan goud er slechts één inneemt. Dus neemt de damp van wijngeest 2100 delen ruimte in waarvan goud er één inneemt; maar lucht, die immers zwaarder is dan de damp, neemt minder delen in. Op welke manier de Ouden beter de verhouding tussen de ruimte van aarde, water, lucht en vuur hadden bepaald dan met een gissing, weet ik niet; ze hebben gezegd dat die is 1 : 10 : 100 : 1000.*) *) Aristoteles had alleen gesteld [als voorbeeld]: 1 maat water geeft 10 maten lucht (de Generatione et Corruptione, Lib. II, cap. 6). De genoemde verhouding komt van de Scholastici. Cardanus nam 50, en Kepler vond (uit lichtbreking) ongeveer 1177 2/3 (Ad Vitell. Paralip., 1604, p. 128). Galileï stelde voor: 460 (brief aan Baliani, 12 mrt 1614). De juiste waarde is ongeveer 1658 [voor water en waterdamp bij 100 °C, en ongeveer 830 voor water en lucht bij 20 °C]. [>] OogoperatieWat ook waarschijnlijk is, en ik heb het eerder geloofd, daar ook veel kleuren en draadjes in de ogen van alle mensen verschijnen, alsof ze aan het genoemde vlies hangen, verder van het netvlies verwijderd. *) O.c. p. 299, Lib. 2, Aforisme 45. |
ProjectielenOf de beweging van projectielen toeneemt.Dezelfde [Bacon, Novum Organum] zegt bij projectielen [300] dat de inslag op een kleine afstand niet zo sterk wordt als wat verder. Wat waar kan zijn bij die welke met buskruit worden afgeschoten, omdat de uitzetting daarvan misschien langer duurt; maar niet bij die welke met de handen, een boog enz. worden geworpen.*) *) Aristoteles (de Coelo, II, cap. 6): het snelst halverwege de baan. St. Thomas en Oresme meenden dit ook. Tartaglia (1546) en Cardanus: daar is het effect van kanonskogels het grootst. Beeckman: het snelst in het begin [<,>]. LichtsnelheidSpecies visibiles an in instanti moveantur.Dezelfde, pag. 305, denkt dat lichtbeelden [species visibiles] meteen, en niet in een merkbare tijd, naar ons stromen, omdat witachige lichamen op een afstand van 60 mijl bij ons meteen te onderscheiden zijn.*)
Maar wie weet of het witachtige lichaam precies op dat mment wordt onderscheiden, waarop het wordt opgeheven? Er is hier namelijk niet zo'n regel als bij geluid, waarvan we met het gezicht waarnemen dat dit het gehoor later treft. Dus wellicht was het witachtige signaal al een hele minuut omhoog gehouden voordat het door ons werd gezien, zo ver er vandaan. *) Beeckman had de eindige lichtsnelheid al verdedigd [<,>]. Dezelfde, pag. 314, heeft ook over ijs, met Keckermann [<] en anderen, een verkeerde mening, denkend dat verdichting altijd door koude komt. Er zijn ook andere van zulke fouten door gebrek aan meer degelijke wiskunde, zoals ik ook bij Basson heb opgemerkt. Dezelfde lijkt overal veel waarde te hechten aan de beweging van onrust*), waarvan hij denkt dat het warmte is; zodat een hele gloeiende kool inwendig onrustig beweegt met zijn heel kleine deeltjes. Waardoor naar hij meent ook een weggegooide steen beweegt, zoals we eerder hebben gezien [<].
[ *) O.c. p. 332 (Afor. 48.18): niet de 'trepidatio' in de sterrenkunde (zie T. 1, p. 21), maar een onrustige beweging van lichamen die als het ware in gevangenschap zijn, b.v. een kloppend hart.] BuskruitSnelle werking van buskruit.Dezelfde zegt*) dat een kleine hoeveelheid aangestoken buskruit veel gewicht opheft, omdat de snelheid van de ontbranding de snelheid van de aantrekking van de Aarde overwint.
Deze overweging zal toch nuttig kunnen zijn voor andere dingen wanneer we begrijpen dat de reden van de overwinning ervan is, omdat dat wat sneller werkt, vaker werkt, terwijl dat wat langzamer werkt, slechts eenmaal werkt. En zo kan dan iets dat zwakker is meer doen door beetje bij beetje te werken, wat ik me herinner ook eerder [<] te hebben gezegd over buskruit. *) Zie p. 306 [Afor. 46]. |
MinimaOf vacuüm met de dingen vermengd is.Dezelfde, pag. 334, gelooft niet dat er vacuüm vermengd is met de dingen*) wegens de verhouding van grotere en kleinere ruimte, omdat er tweeduizend maal zoveel vacuüm zou zijn in lucht als in goud, en zo zouden de luchtdeeltjes rondzwerven zonder effect, zoals stofjes.
Toch is het niet nodig te stellen dat de kleinste 'homogenea' [<] van lucht kleiner zijn dan de kleinste homogenea van aarde, maar dat ze bestaan uit veel atomen, verbonden tot cirkels [<]. Waarom zouden ook niet homogenea van aarde in de poriën van glas dringen, als ze zo gemakkelijk van elkaar gescheiden worden, wat blijkt bij water, dat tenslotte uit een met glas afgesloten flesje door kalme warmte geheel uitwasemt. [ *) Vergelijk Beeckmans tweede stelling bij zijn promotie, 1618.] SamenvattingNovum Organum van Verulam kort samengevat.Aangezien hier*) dit Novum Organum niet te koop is, wil ik in het kort samenvatten wat Franciscus hier leert, het zal me misschien nog eens van pas komen. Hij leert dus de natuur der dingen niet te onderzoeken met het syllogisme, maar met een meer volkomen inductie. Bijvoorbeeld, bij het zoeken naar de natuur van het warme, maakt hij eerst°) een tabel, waarin hij alle dingen bijeenbrengt die op een of andere manier deel hebben aan warmte, die hij noemt bevestigende gevallen. Ten tweede voegt hij hierbij de negatieve gevallen, als ze erbij zijn. Een bevestigend geval kan zijn: de stralen van de Zon zijn warm; een negatief geval: de stralen van de Zon zijn niet warm in het midelste gebied van de lucht. Uit zulke negatieve gevallen ontstaat een tweede tabel. Ten derde maakt hij een tabel van zaken die met andere worden vergeleken in warmte en dat is de tabel van de graden. Ten vierde maakt hij een tabel waarin hij alle zaken vermeldt die hij uitsluit uit de natuur van het warme; hij vindt ze met de drie voorgaande. Bijvoorbeeld: daar de stralen van de Zon warm zijn door de natuur van het warme, is deze niet elementair; deze natuur is immers altijd aanwezig, of afwezig, of neemt met het warme toe, of neemt af; als dus veel zaken zijn uitgesloten, is het noodzakelijk dat de vorm van het warme iets is van wat er overblijft. Ten vijfde laat hij het verstand uit dat overblijvende kiezen wat het wil, en dat noemt hij de eerste oogst, en hij bekijkt dan of dit de vorm van het warme zou kunnen zijn. En zelf denkt hij zo te hebben gevonden dat de natuur van het warme is: beweging. Ten zesde, daar beweging te algemeen is, en hij ziet dat niet elke beweging warmte is, beproeft hij de ene of de andere beperking, en die noemt hij het eerste verschil, enz. naar gelang hij veel verschillen nodig heeft. Hij zegt dan dat warmte is een uitzettende beweging; ten tweede een beweging naar de omtrek; ten derde met kleinere deeltjes van het lichaam en tegelijk geremd en teruggeduwd; ten vierde niet langzaam maar vlug, door niet te kleine deeltjes; over deze onrustige beweging hebben we ook eerder iets gezien. [<] *) Waarschijnlijk niet alleen in Middelburg, maar ook in Holland. °) 1: o.c. p. 166 (Lib. 2, Afor. 11), 2: 169 (12), 3: 189 (13), 4: 207 (18), 5: 211 (20), 6: 213 (20). |
|
Ten zevende*) stelt hij 27 voorkeursgevallen, waarmee de natuur van een zaak nog makkelijker wordt verklaard en nauwkeuriger tabellen kunnen worden opgesteld. En in het eerste boek°) had hij de belemmeringen laten zien, waarom de wetenschappen in zoveel eeuwen niet duidelijk gevorderd zijn, waarvan hij ongeveer zegt dat er vier soorten idolen zijn, die het denken van te voren in beslag nemen, namelijk idool van de stam, van de grot, van de markt, van theorieën. Vervolgens vestigt hij de hoop, met deze kunst de wetenschappen te verbeteren en te bevorderen enz. *) 7: o.c. p. 221 - 357 (Afor.22 - 51). °) O.c. p. 57 [Lib. 1, Afor. 39: Idola Tribûs, Specûs, Fori, Theatri] en p. 63-71 [Afor. 50 - 63]. [ Skepsis, 'Justus von Liebig over Francis Bacon', 1863/1874, vert. Jan Willem Nienhuys. Th. Fowler, Bacon's Novum Organum (Oxf. 1889), p. 143: "Liebig's onslaught on Bacon ... bitter ... inaccurate ... contributes nothing new". Meer waardering voor Lasson (zie bij Skepsis).] |
Druppel op stofEen druppel lijkt stof te ontvluchten, maar een druppel te volgen, waarom.Baptista Porta zegt in Pneumaticorum Lib. I, cap. 9,*) dat een waterdruppel bij droog stof gebracht vlucht en tot een bolvorm wordt gedwongen; maar dat die, gebracht bij een andere druppel, zich meteen daarmee verenigt wegens de gelijkheid van aard.°) Maar de reden hiervan lijkt, omdat het stof het water niet precies raakt wegens de grote poriën die in het stof schuilen, zodat lucht die nog tussen die poriën zit de druppel raakt en met zijn druk de ronde figuur in stand houdt. *) Io. Bapt. Portae Neapolitani Pneumaticorum Libri tres (Napels 1601), p. 14. °) Vergelijk T. 1, p. 42: "twee druppelkens, die malkanderen int minste maer en genaken ...". Francis Bacon [<,>] zegt hierover, Novum Organum, p. 230 [Afor. 25]: "wegens het verlangde samengaan van water met water en van lucht met lucht", en op p. 316:
|
|
En een druppel raakt een druppel zo, dat er geen lucht tussenkomt, maar dat een groot deel van een grote druppel, nauwkeurig en onmiddellijk vasrzit aan een deel van de andere druppel; en zo worden beide druppels door de leunende lucht tot vereniging gedwongen, daar er tussen de druppels niets in de weg zit dat de kracht van de lucht tegen ze verzwakt. Deze reden zal misschien ook overgebracht kunnen worden op de samenvoeging van dingen of van homogenea [<] die zich in vacuüm verspreiden, waar niet zo'n samendrukking is. |
| Euclides, Lib. I, Prop. 26, zegt dat βγ gelijk is aan εζ omdat de hoeken βαγ en αγβ gelijk zijn aan de hoeken εδζ en δζε, en de lijn αγ gelijk is aan de lijn δζ. Wat Theon*) bewijst uit het ongerijmde, zoals het hem wel toeschijnt, want het is voor hem ongerijmd, als de mening van het tegengestelde de omverwerping van een hypothese kan opleveren.°) |
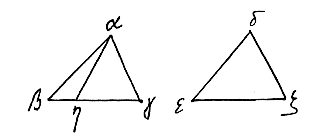
|
Maar, zeg ik, de weerlegging van een hypothese, die Theon zelf heeft gesteld, is niet ongerijmd. Want als hij een onware hypothese zou hebben gesteld, zou hij met dezelfde noodzaak hebben geconcludeerd. Bijvoorbeeld: ik zeg dat βγ gelijk is aan εζ, als hoek βγα het dubbele is van hoek εζδ, en hoek βαγ gelijk is aan hoek εδζ. Als je het ontkent, laat ηγ dan gelijk zijn aan εζ, en trek αη. Dan zal, volgens de vierde van het Eerste, hoek ηαγ gelijk zijn aan hoek εδζ. Maar βαγ is ook gelijk gesteld aan εδζ, dus ηαγ is gelijk aan βαγ, een deel aan het geheel. Je ziet dus dat de weerlegging van een eigen hypothese niets noodzakelijk concludeert, wanneer op die manier iets onwaars wordt bewezen als waar.
*) Theon Alexandrinus, Euclidis quindecim Elementorum Geometriae primum; ex Theonis Commentariis ... Authore Cunrado Dasypodio (Argentini 1564). Prop. 26 op p. 80 e.v. [ °) Op p. 180 (bij 'Scholia'): "herleiding tot het onmogelijke, wanneer we uitkomen op iets dat duidelijk absurd is, en waarvan iedereen erkent dat het tegengestelde waar is".] |
Omkering van een stellingAxiomatisch gevolg toegeschreven aan Theon over Euclides.Ten onrechte heb ik in het voorgaande stukje Theon berispt alsof het niet ongerijmd zou zijn, als de mening van het tegengestelde op die manier de omverwerping van een hypothese zou opleveren.
Er zijn namelijk enige niet-syllogistische argumenten, die een gevolgtrekking maken met alleen een axiomatisch gevolg, wat de Logici noemen: omzetting van de propositie*). Zo wordt de algemeen bevestigende omgekeerd met het bijkomstige, dat wil zeggen tot een bijzonder bevestigende. Als iemand dus zou betwijfelen of enig dier een mens is, zou ik hem dit kunenn bewijzen, omdat elke mens een dier is, wat hij misschien beter zou aanvaarden.
Zodanig is propositie 26 [<]. Hij zegt namelijk: Als van twee driehoeken, twee hoeken en de zijde ertussen gelijk zijn, is ook een andere zijde enz. gelijk; want als die andere zijde van de twee driehoeken niet gelijk is, zijn de twee hoeken en de zijde ertussen niet gelijk. Hij toont namelijk aan dat één hoek niet gelijk is aan een andere van de twee met de hypothese dat ze gelijk zijn, omdat anders een deel gelijk zou zijn aan het geheel, of (wat op hetzelfde neerkomt), als de hypothese blijft staan, is een deel gelijk aan het geheel. De propositie nu van Euclides, die Theon zo bewijst, vooronderstelt veel, zodat hij het ene of het andere, of ook een derde concludeert. Het was dus voldoende (zoals hij deed) bij de omzetting slechts één hypothese omver te werpen; want het was noodzakelijk dat al het voorgaande waar was, om het ene gevolg waar te maken, en daarom, als het gevolg niet waar is, is het voldoende dat één voorgaande niet waar is.
Iets dergelijks is dit: Als ik groter ban dan jij, en jij bent groter dan Pieter, ben ik groter dan Pieter; want als ik niet groter ben dan Pieter, ben ik niet groter dan jij, of ben jij niet groter dan Pieter. Het is namelijk voldoende de onwaarheid van één van beide te hebben bewezen, om de waarheid van de eerste propositie te bevestigen. Want ik leid die hypothetisch af met het syllogisme: [ *) Vergelijk Simon Stevin, Bewysconst, p. 89: "Regulen vande verkeeringhe der propositien".] |
Hypothetische propositiesHerleiding van hypothetische proposities naar categorische.Bijna hetzelfde gebeurt bij het naar voren brengen van hypothetische proposities, zoals: Als Pieter een mens is, is Pieter een dier, want elke mens is een dier. Deze reden is zo duidelijk, dat die niet kan dienen om syllogistisch een hypothetische propositie te bewijzen; dit is namelijk gegrond op het axioma: als van iets de soort [species] bekend wordt gemaakt, wordt daarvan ook het geslacht [genus] bekend gemaakt.
Daarom, liever dan dat je iets anders aanvoert, is het beter te zeggen:
Er zijn ook hypothetische proposities die hun eigen reden verschaffen, zoals: |
|
Zo ook: Als Pieter een mens is, is Bucephalus een paard; want Pieter is een mens en Bucephalus is een paard; het eerste voorzover Pieter als subject aan een mens wordt toegekend, zoals Bucephalus aan een paard; het laatste voorzover mens over Pieter wordt gezegd als predikaat, zoals paard over Bucephalus. En zo wordt dan de hele redenering ingericht en onderzocht volgens die hypothetische proposities, die hun reden in zich hebben. [>] |
Oefening voor leerlingenOefening met vijdelig syllogisme aan mijn leerlingen voorgelegd.De oefening die ik gisteren "den 12en Octob." [Nov.] heb voorgelegd aan mijn leerlingen van de eerste klas, houdt het midden tussen disputeren zonder meer en een woordenkraam, te weten op de manier waarop mensen uit het volk gewend zijn met elkaar te debatteren. Ik zou dus willen dat zij voortdurend dezelfde volgorde in acht nemen, zodat ze aan de hand daarvan ook eens leren voor de vuist weg zo met elkaar te disputeren over een voorgelegde zaak. |
|
Hier zal ik de disputatie zonder meer voorleggen, en met deze volgorde moeten ze zelf verder gaan. Zij moeten de afzonderlijke proposities omkleden met retorische figuren, en van het vijfdelige syllogisme, dat volgt, de major- en minorpremissen bevestigen in voorsyllogismen, als ze willen. Of liever moeten ze één van beide premissen uitbreiden, dat wil zeggen: als je de major niet hebt uitgebreid, doe het dan met de minor. En de hoofdconclusie moet je prachtig uitbreiden met stijlfiguren; vooral volgens Alsted [<]: door het tegengestelde, door vergelijking, door deling, door getuigenis, en dit bij predikaat en subject. Zo moet je ook één van beide conclusies in de voorsyllogismen uitbreiden. En zo heb je dan de vijf termen uitgebreid, die als enige in het vijfdelige syllogisme voorkomen. Het schema van de eerste oefening bestaat in die proposities in de volgorde, die ze in het vijfdelige syllogisme hebben; en dit is de basis van allemaal.
SCHEMA VAN EERSTE OEFENING
Een bepaalde vis heeft een ziel, | ||||||||||||||||||||||||||||||||||||
|
SCHEMA VAN WEERLEGGING
Je zegt: Een bepaalde vis heeft een ziel, wat je niet goed hebt bewezen,
Ik zeg nog altijd: Een bepaalde vis heeft een ziel,
Je zegt: Een bepaalde vis heeft een ziel, wat je niet goed hebt bewezen, |
|
INDELING VAN SLECHTS ÉÉN ORATORISCH SYLLOGISME
Een bepaalde vis heeft een ziel,
Wat dubbelzinnige termen betreft, zullen ze een beperking kunnen toevoegen aan een term zelf, zoals ze denken dat de tegnestander die stelt; of als ze twijfelen, dat syllogisme waarin een term dubbelzinnig is, met een tegengestelde beperking in dezelfde volgorde herhalen. Hier lijkt nu hoegenaamd niets verder te moeten worden uitgebreid dan wat bij het vijfdelige syllogisme is gezegd. Het zijn immers slechts gevolgen van gevolgen. Het is voldoende het te hebben versierd met stijlfiguren: ondervraging, uitroep enz.
Je zegt: Een bepaalde vis heeft een ziel, wat je niet goed hebt bewezen,
Je zegt: Een bepaalde vis heeft een ziel, wat je niet goed hebt bewezen, |
|
WEERLEGGING WANNEER DE MIDDENTERM DUBBELZINNIG IS
Je zegt: Een bepaalde vis heeft een ziel, wat je niet goed hebt bewezen,
Want een bepaalde vis is wel een mens, oneigenlijk gezegd,
Je zegt niet, geloof ik: Een bepaalde vis heeft een onredelijke ziel, want dit erken ik,
Je ontkent: een bepaalde vis heeft een ziel, |
Men moet nu niet denken dat altijd moet worden verder gegaan in de volgorde die ik heb voorgesteld, maar men kan bij een vijfdelig syllogisme eerst de eerste major bewijzen en sommige proposities naar wens veronachtzamen als duidelijk, of ondergeschikt, ja zelfs zijdelings bewijzen. Zo had hier bij het vierdelige de major bewezen kunnen worden, zoals nu de minor is bewezen; ook had met slechts een enkel syllogisme de minor bewezen kunnen worden. Als we het ene of het andere maar voor zeker houden, of wat weggelaten is, of zijdelings enz. bewezen. Wat zou kunnen gebeuren moeten we goed weten, opdat we altijd langs een heel zekere weg naar een voorraad en samenvattingen kunnen gaan, als we dat willen. Hypothetisch (2)Herleiding van hypothetisch tot categorisch syllogisme.Hyothetische syllogismen, waarin de termen niet ondergeschikt zijn, zijn ook op een andere manier dan ik eerder gezegd heb [<] tot categorische te herleiden, namelijk met die term die weliswaar niet is uitgedrukt, maar waardoor het gevolg geldig is, met weglating van een neventerm. Bijvoorbeeld: Zo volgen sommige gevolgen niet onmiddellijk, maar indirect, zoals: | ||||||||||||||||||||||||||||||||||||
|
Hetzelfde is te ondervinden bij alle vijf manieren van gevolgen. Zo bij de vijfde manier van gevolgen, waar vier verschillende termen zijn, en ze kunnen slaan op de vier eerste manieren van gevolgen, en de daaraan ondergeschikte, zoals:
Evenzo is de omverwerping niet overal gelijk, want waar het subject tweemaal wordt herhaald, daar is ook geschikt de 'oppositio subcontraria'*), zoals:
In andere gevallen is alleen geschikt de omverwerping met tegenspraak, zoals:
Evenzo beschikken we hypothetisch met slechts twee termen over een argument op basis van omzetting van de proposities, zoals: [ *) Zie Alsted 1614, p. 362: "Subcontraria oppositio" is de strijdigheid tussen twee bijzondere axioma's alleen volgens een kwaliteit. Zoals: ... Een bepaalde mens is geleerd, Een bepaalde mens is niet geleerd. ... ze kunnen niet tegelijk onwaar zijn.] |
Gebrekkige syllogismenOplossing van gebrekkige syllogismen.Iedere zonde is tegen God; maar een bepaalde zonde is tegen de naaste; dus een bepaalde naaste is God. In ieder hoofd zijn hersenen; maar in ieder hoofd is een neus; dus een bepaalde neus, dat zijn hersenen. Iedere leugen heeft God verboden; iedere leugen heeft Mozes verboden; dus Mozes is God. Aan iedere mens zijn oren; maar aan iedere mens is een neus; dus een bepaalde neus, dat zijn oren. Iedere leugen heeft God verboden; maar een bepaalde zonde is een leugen; dus een bepaalde zonde heeft God verboden. Aan iedere mens zijn oren; Pieter is een mens; dus aan Pieter zijn oren. Al deze syllogismen zijn gebrekkig, uitgezonderd de twee laatste, deswege omdat het predikaat, zoals het uit de conclusie wordt gehaald, niet gezegd kan worden over het subject; want de conclusie geeft aan dat God een predikaat is, maar God is niet wat als predikaat gezegd wordt over iedere mens die een zonde verbiedt. Zonde is immers niet een deel van een subject dat een kwantiteit vereist, omdat het niet wordt aangebracht met een ware koppeling. |
|
Zo wordt neus niet als predikaat gezegd over de mens, want het omvat hem niet met zijn kwantiteit, maar oren hebbend wordt wel over iedere mens gezegd, en iets wat God verboden heeft, wordt als predikaat gezegd over iedere zonde. Als dus een waar predikaat wordt overgebracht in de conclusie, zullen syllogismen goed zijn, anders gebrekkig; niet zoals in de tweede figuur*) op grond van zuiver bevestigende, omdat ware predikaten daar middenterm zijn, en een waar subject in de conclusie een predikaat is.
Nu wordt er anders gehandeld met subjecten dan met predikaten, omdat subjecten nauwer kunnen zijn dan predikaten en ze nooit ruimer zijn dan deze; en daarom is het geen wonder als een fout wordt begaan in de derde figuur op grond van dezelfde proposities uit de tweede figuur, maar dan omgezet. Laat dus strikt in acht genomen worden de regel over Elke [<] en laten we ons eraan houden dat de naamvallen aangeven of in conclusies de termen goed of slecht worden herhaald; en laten we onderzoeken of niet een grotere identiteit wordt vereist van subjecten dan van predikaten, daar de eerste de grondslag zijn, en de laatste breder en bijna naar wens worden genomen, en zo mogen ze dan ook zondigen tegen de regel bij het syllogisme: dat er niet meer dan drie termen zijn. Toch moet bovenal bezien worden op grond van de conclusie, of de premissen goed verdeeld worden in ware subjecten en predikaten, zoals we zien. Dit geeft de conclusie namelijk aan, die predikaten van subjecten scheidt; want als de eerste hier nauwer of gelijkwaardig bevonden worden, zijn het geen behoorlijke predikaten en dan zijn de argumenten gebrekkig. [ *) Zie Stevin, Bewysconst, p. 36-37, tweede soort: "Alle ghedierte leeft, Gheen turf en leeft, Gheen turf dan en is ghedierte".] Als papegaai roepend: 'niet waar'Respondent die slecht antwoordt tot de orde roepen, hoe.Om ervoor te zorgen dat respondenten niet ook aan het alleronwaarste kunnen blijven vasthouden, steeds op dezelfde toon herhalend als papegaaien [<] "we ontkennen de major", "we ontkennen de minor", ook als ze heel waar zijn:
ten eerste, als de ontkende propositie bijzonder is, brengen we de respondent naar iets dat onmogelijk is. Want met een ontkende bijzondere propositie is hij makkelijker tot iets onmogelijks te brengen, omdat zijn tegensprekende propositie algemeen is, waarmee noodzakelijkerwijze één van de premissen vaststaat; ook kan een bijzondere propositie heel makkelijk bewezen worden in alle figuren en in de derde door expliciete uitdrukking.
Daarom, wanneer we al enige keren met iets vrij duidelijks hebben bewezen en de respondent duidelijke algemene proposities lijkt te ontkennen, hetzij door onwetendheid, hetzij door gemakzucht, gaan we die bewijzen door inductie en gaan we vragen naar een geval. En als hij dit naar voren brengt, gaan we het tegengestelde van het afzonderlijke geval bewijzen, of gaan we de respondent met dat geval naar iets absurds brengen. |
|
Als hij geen enkele reden heeft gegeven, moet de inductie herhaald worden en is de respondent overwonnen; en de overwinning is des te aanzienlijker, naarmate aangetoond wordt dat deze algemene propositie meer afzonderlijke gevallen of lagere soorten in zich bevat. Ja zelfs ook als de opponent zijn algemene propositie zo heeft beperkt, dat die slechts twee of drie afzonderlijke gevallen bevat; de respondent had toch zo voorbereid aan het disputeren moeten beginnen, dat hij zijn stelling met reden zou kunnen scheiden van die welke de opponent voor hem aan zijn algemene propositie had verbonden.
Als dus de respondent een reden heeft gegeven, zal die zijn met het tegendeel van de conclusie, of met een enthymeem voor de stelling. Stilzwijgend moet dus bezien worden welke propositie wordt verlangd en van deze, of van de uitgedrukte, moet het tegendeel bewezen worden; en zo zal dan tot het eind van de disputatie gekomen kunnen worden, en de respondent zal niet in slaap kunnen komen en de waarheid zal de overhand hebben.
Bijvoorbeeld: Een syllogisme van de opponent was:
Zo: Alle planeten zijn groter dan de Aarde; maar de Maan is een planeet; dus de Maan is groter dan de Aarde. |
Of 'niet' bij een term hoortOf het woordje niet altijd als deel van een term te zien is.Aangezien het ontkennende woordje "niet" in alle figuren wordt aangetroffen als deel van een term, waarom wordt het dan niet als zodanig beschouwd? En wanneer gezegd wordt: de conclusie volgt uit het zwakkere deel, is dit hetzelfde als wanneer gezegd zou worden: de hele majorterm moet in de conclusie herhaald worden, dat wil zeggen opdat er niet meer dan drie termen zijn. Maar in de tweede figuur lijkt die scheiding noodzakelijk, en wel opdat er tenminste oneindig vaak iets tegenover de predikaten gesteld kan worden; want uit proposiies waarvan er één oneindig is (die toch bevestigend genoemd wordt), volgt de conclusie, zoals in: Elke mens is dier; maar elke steen is niet dier; dus elke steen is niet mens, of: geen steen is mens. Doch in de eerste en derde figuur zien we bevestigende minoren, genomen niet als deel van een term. Dus het ontkennende: Geen mens is steen, is daar niets anders dan: Elke mens is iets dat niet steen is; elk dier is iets dat niet mens is. Dus alleen door oneindig tegenover stellen in de tweede figuur wordt elke ontkenning in syllogismen opgelost. [>] Bacon: water wordt luchtWater wordt niet lucht, bewezen met glas waarmee warmte wordt onderzocht.Den 12en Decemb. 1623. Francis Bacon [<,>] zegt in zijn Historia ventorum*), bij Artikel 8 van het onderzoek van bijzondere onderwerpen, Aforisme 23, pag. 111, dat water in lucht verandert en een honderd keer zo grote ruimte inneemt, en daarom meent hij in heel deze Historia dat water op een heel gemakkelijke manier ontbonden wordt tot dampen, en dat zo terstond nieuwe lucht ontstaat.
Maar hier lijkt hij door te slaan, daar hij van deze omzetting nergens een aannemelijk argument naar voren heeft gebracht. En ook: in de dagglazen, waarmee we de koude en warmte van het weer onderzoeken [<], zou de lucht in korte tijd vermeerderd of verminderd zijn, en dan zou dit instrument bijna geen nut hebben. *) Francisci Baronis de Verulamio, Vice-Comitis Sancti Albani, Historia naturalis et experimentalis (Londen 1622). Dit is deel 3 van de Instauratio Magna, met 'Historia ventorum' op pp. 29 - 246. [Heruitgave van dit deel: Leiden 1648, p. 44.] Grote en kleine schepenOf grotere schepen langzamer bewegen dan kleinere.En op pagina 170 meent hij dat kleinere schepen in snelheid de grotere ver overtreffen, omdat grotere zeilen beter passen bij een klein schip dan bij een groot schip, naar verhouding van de omvang, niet wetend dat een belangrijke oorzaak van snelheid is: de zwaarte van een schip dat eenmaal in beweging is. Wnnneer dit namelijk eenmaal in beweging is, blijft het veel langer doorgaan met deze beweging dan een kleiner lichaam, waardoor het komt dat enige toegevoegde beweging de vorige beweging vermeerdert, voordat deze zou zijn afgenomen; ja zelfs: een lichter lichaam krijgt niet een zo snelle beweging als een zwaarder lichaam, daar lucht en water zich minder verzetten tegen het zwaardere dan tegen het lichtere, naar verhouding van de lichamelijkheid en het oppervlak, zoals we ergens eerder hebben uitgelegd [<]. |
Hogere zeilenHoe hogere zeilen een schip sterker voortbewegen.En op pag. 173 meent hij dat de wind een schip meer voortbeweegt in hogere zeilen dan in lagere zeilen, door vergelijking met hefbomen, zeggend: een hevige beweging heeft de meeste uitwerking waar heel veel van de weerstand wordt weggenomen, zoals bij hefbomen. Maar bij hefbomen is een bepaalde as in rust, en daar worden ongelijke armen beschouwd, wat hier niet het geval is, aangezien alles tegelijk beweegt op dezelfde manier. Ja zelfs als het waae zou zijn wat hij zegt, zou een paard in de hoogte een lager schip, of een lagere wagen, makkelijker en sneller voortbewegen dan in hetzelfde vlak, wat niemand zal hebben bewezen. Lucht is zwaarLucht is zwaar.Hij meent eveneens, op pag. 230, dat bij lucht elke beweging van zwaarte afwezig is en dat die daarbij iets ontneemt aan de beweging van water. Waarvan ik het tegendeel hiervoor [<] heb laten zien, namelijk dat lucht ook zwaar is en dat daarom hier niet minder ontstaan vocht in achterblijft dan in water. En het vocht komt van water dat in damp is opgegaan, of van verdunde lucht, zoals hij zelf goed zegt, en zoals ik eerder heb laten zien [<] dat dit vocht zich uitstrekt tot het oppervlak van de lucht en daar golvend beweegt. |
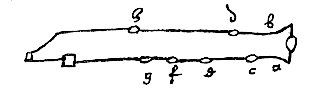
| a | pink van rechterhand. | klinkt met alle gaten dicht | ut | |
| b | ringvinger van rechterhand. | c open klinkt | re | |
| c | middelvinger van rechterhand. | c, d open klinken | mi | |
| d | duim van rechterhand. | c, d, e open klinken | mi | |
| e | wijsvinger van rechterhand. | c, d, e, f open klinken | ut, sol | |
| f | middelvinger van linkerhand. | c, d, e, g open klinken | re, la | |
| g | wijsvinger van linkerhand. | c, d, e, f, g open klinken | mi | |
| h | duim van linkerhand. | c, d, e, f, g, h open klinken | fa | |
| h alleen open, overige dicht | sol |
|
Dit is de inrichting van pijpen die onze Basirius heeft gebruikt in Frankrijk te Rouen.*) [<]
*) Beeckman was in Rouen in 1612 [<]. Toen was Jean Titelouze (1563 - 1633) daar organist van de kathedraal. [Brief aan Mersenne over een vraag van Beeckman: IV, 169.] [ "Noster Basirius", Wikipedia: Isaac Basire (1607-1676), "at sixteen he was sent to school in Rotterdam". Na 1646: "Basire commenced his travels by visiting Rouen, where he had a small patrimony".] Regels in de muziekEnkele regels bij muzikale toonsoorten.Wat ik elders [<] begonnen ben vast te stellen over de muzikale toonsoorten, niet alsof het voortdurend in acht genomen moest worden, maar dat zulke liederen eleganter zijn, daarvan zijn enige gedeelten samengevat in een of ander handgechreven boek, uit Frankrijk meegebracht*), in dit toevoegsel: I. Bij moduleren, van kwint naar kwart en andersom, gaat de overgang alleen met de karakteristieke. Aangetoond is namelijk dat de karakterisitieke de toonsoort aangeeft; als deze dus afgelopen is, zal de toonsoort open liggen (en characteristicon noemt hij wat ik de middelste hoofdnoot noem, zoals de la in de eerste toonsoort re la sol).
II. Een interval van zes of zeven noten wordt van modulatie uitgesloten. De drie voornaamste intervallen van een toonsoort zijn (zegt hij): octaaf, kwint en kwart. Verder zijn binnen de grenzen van een kwart toegelaten de intervallen halve toon, toon, tweetoon en anderhalve toon. III. Veelvuldige herhaling van de karakteristieke noot is niet het laatste middel voor de uitersten. De karakteristieke en de uitersten hangen namelijk samen, daarmee is de toonsoort bekend gemaakt. IV. Begin en pauzes moeten gegeven worden aan de karakteristieke of aan de uitersten. Daar immers begin en pauzes aanhoudender en indringender de oren treffen, worden ze met recht toevertrouwd aan de karakteristieke en aan de uitersten, die leidend zijn voor de toonsoort. [>] [ *) Wellicht door Isaac Basire, zie de vorige noot.] |
Syllogisme met voorwaardeHerleiding van hypothetische syllogismen.Herleidingen van hypothetische syllogismen tot categorische geven te kennen wanneer bij die hypothetische in het algemeen geconcludeerd kan worden, en wanneer in het bijzonder, als maar niet hetzelfde tweemaal subject is. Hiermee zul je ook wel eens zien, door de kracht van de vierde figuur, dat het gevolg waar is enz.; eveneens dat soms iets wordt voorondersteld waarmee het gevolg waar is enz., zoals ik eerder ergens heb gezegd [<]. Maar laten we nu herleidingen bekijken in de volgorde vanaf stelling van het voorgaande tot stelling van het volgende: |
| Als elke mens een dier is, is elke mens een schepsel; | Elk dier is een schepsel; | |
| Maar elke mens is een dier; | Maar elke mens is een dier; | |
| Dus elke mens is een schepsel. | Dus elke mens is een schepsel. | |
| Als elke mens een dier is, is enig schepsel een mens | Elke mens is een dier; | |
| Maar elke mens is een dier; | Elk dier is een schepsel; | |
| Dus enig schepsel is een mens. | Enig schepsel is een mens. | |
| Als elke mens een dier is, spreekt enig dier; | Elke mens spreekt; | |
| Maar elke mens is een dier; | Elke mens is een dier; | |
| Dus enig dier spreekt. | Enig dier spreekt. |
| Als elke mens een dier is, spreekt enig dier; | Elke mens is een dier; | |
| Maar elke mens is een dier; | Elke mens spreekt; | |
| Dus iets dat spreekt is een dier. | Iets dat spreekt is een dier. | |
| Als elke mens dier is, is alles wat spreekt schepsel; | Elke mens is een schepsel; | |
| Maar elke mens is een dier; | Alles wat spreekt is een dier; | |
| Dus alles wat spreekt is een schepsel. | Alles wat spreekt is een schepsel. | |
| of | De minor wordt bewezen: | |
| Elke mens is een schepsel; | Elke mens is een dier; | |
| Alles wat spreekt is een mens; | Alles wat spreekt is een mens; | |
| Alles wat spreekt is een schepsel. | Alles wat spreekt is een dier. | |
| De major wordt bewezen: | ||
| Elk dier is een schepsel; | Hetzelfde vanaf omstoting van volgende tot omstoting van voorgaande, en bij beide met veranderde hoeveelheid. | |
| Elke mens is een dier; | ||
| Elke mens is een schepsel. |
| [>] |
Redenering weerleggenHoe de redenering van een respondent wordt omgestoten.Wanneer bij stellingen een of andere reden wordt gegeven, en de opponent vindt die niet goed, wordt soms gevraagd, hoe dit aan de toehoorders kan worden aangetoond en hoe daarbij een reden gegeven kan worden.
Ik antwoord op de manier waarop ik even hiervoor [<] heb verteld, hoe het gevolg van een hypothetische propositie wordt bewezeb met een categorische conclusie. Bijvoorbeeld, laat de stelling zeggen: |