Vorm van een schip Navis optimae proportio, quî imitanda.   Also ick Vincent Everdeys [<] geleert hadde alderhande forme in syn silversmits ambacht te vergrooten ende te verkleynen, tot groot gemack, dewyle dattet niemant te Middelburgh doen en kan — maer elck gaet van syn nabuer een mate leenen, die al tastende gevonden is ende nochtans ontbrekender noch oneyndelick veel grootheden — also quam my oock daerdoor in den sin, dat hetselfde oock in schepen geschieden kan.   Alser dan een schip is, dat uyttermaten wel seyldt, men sal na datselvighe een grooter, kleynder, soo men wilt, maken, dat oock so wel seyle, de seylen, ladinghen ende alles proportionerende; ende letten daerop, dat sommighe dynghen cubyckxwyse moeten geconsidereert werden, sommighe quadraetswyse, sommighe lineaelswyse. Also salmen alles na de grootte, ladinghe, wint etc. proportioneren.   Dan het gebeurt dicwils, dat het fatsoen van een groot dinck anders moet syn dan van een kleyn, omdat het somtyts anders gebruyckt wort. Want kleyne potkens fatsoeneert men so, dat mer oock uyt soude konnen dryncken, twelck in groote potten niet geschien en kan, maer daer schept men uyt. Doch meestendeel begeert men yet groots alleenlick om ten toone te stellen ende te proncken opt fatsoen vant kleyne, gelyck men siet dat die heel groote roomers gemaeckt worden tot anders gheen gebruyck. Want alle dynghen worden eerst op een bequame grootte gemaeckt nae het gebruyck; ende dan, tot plaisier, worden daer na gemaeckt alderhande grootheden, als huysen, palleysen, tafels, saelen, bekers, beelden, etc. Stok in water Baculus in aqua erectus, cur cadat.   Om te beginnen te mediteren op schepen*), so dencke ick vooreerst op de reden waerom dat eenen stock niet overeynde in het water staen en kan? De reden is, omdat het deel buyten het water leegher, ende het deel onder het water hoogher soeckt te syn. Ende also draeyt den stock op den diameter des cirkels, die gemaeckt wort van de gemeyne sne des stockx ende des waters.   *)  Beeckman kende alleen het werk van Stevin, en niet dat van Archimedes [<], wiens de Iis quae vehuntur in aqua in 1565 door Commandino gepubliceerd was. Galileï werkte ook aan dit onderwerp: Discorso ... Intorno alla cose, che stanno in su l'aqua, o che in quella si muouono (1612) [Eng. 1663], en Huygens rondde het af (1650): 'de Iis quae liquido supernatant', in Oeuvres XI (1908), 93-210  [Ned. not.].

[ 257 ]

Ten anderen, als men een mathematische linie int water stelt, ende aen elck eynde eenen knoop van houdt, welck houdt effen eens so licht is als het water, ende dat den ondersten houten knoop eens so groot is als den oppersten, so sal den mathematischen stock so diep ingaen als men hem stelt, dat is alle gestalt houden, als men slechs maeckt dat hy niet omverre en valt. Men mach wat beter hier op letten oft met reden bestaet.   Ten derden so kanmen weten wat proportie het water teghen het houdt heeft. Want neempt eenen pylaer gelyck een effenen stock, ende laet die int water syncken, dat se niet en valle, hem ter syde, steunende, ende besiet hoeverre datse insinckt, ende seght dan: gelyck hem houdt de grootte van het stuck onder het water teghen den heelen stock, so heeft hem de swaerte des houdts teghen de swaerte des waters. Want den stock maeckt int water eenen put, daer so veel gewicht waters in mach als den stock weeght. Gewicht van gedeelte Ligni pars non separati, quanti sit ponderis.   Ten vierden kan men hierdoor weten, hoe swaer een stuck houdts is, al blyft het aen het geheel houdt, daer ick te vooren dickwils op gedocht hebbe ende mentie van gemaeckt [<]. Want door den effenen stock de proportie van het water en het hout gevonden hebbende, laet den oneffenen stock int water syncken ende saeght het houdt in twee stucken, daert aen het opperste van het water raeckt, so sal het stuck teghen het ander syn, gelyck het een teghen het ander soude syn van den effenen stock, dat is, gelyck de swaerte van het houdt is teghen de swaerte van de reste van het water, daer de swaerte des houdt afgetrocken is. Maer so dat stuck niet en is het begeerde, so moet ghy met soudt, of andersins, het water veranderen om een ander proportie te hebben.   Also kondt ghy oock weten, hoeveel dat een middelstuck weghet, daervan het een eynde aen het een water, ende het ander aen het ander water gerocht heeft. Men kan oock, met het soudt te weghen, de proportie van het water na begeeren veranderen. Ende so dat noch niet en voldoet, daer is brandewyn, oly, quicksilver etc.   [>] Stok recht in water Baculum in aqua erigere.   Ten vyfden, alsmen eenen stock in water recht wilt doen staen, so moet men daer onderaen so veel loots doen dat het styver neerweeght dan het houdt int water opwaerts ende buyten het water nederwaerts, considererende dat de gemeyne sne des waters ende stockx den as is daer den stock op draeydt, also dat de deelen des stockx daer verst van synde, meest weghen. Maer dewyle doort aendoen des loots den stock noch dieper synckt, so salt best syn te ondersoecken de proportie des loots teghen de reste des stockx, die alree recht int water staet.

[ 258 ]

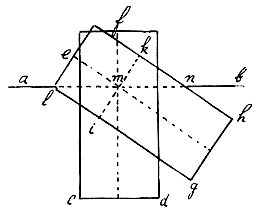
Ten sesten so salmen principalick letten op den as, want als het houdt alreede recht staet, so en kandt niet wel vallen, omdat het deel dat int water kompt ende dat uyt het water ryst, beyde helpen tot het rechten, want het eene is aen d'een syde ende het ander aen dander syde des asch, volgens dese figure, na order der weeghkonstighe balancen: fcd staet recht, door wat oorsaken het oock soude moghen wesen; ab is waters oppervlack. Den wint, of yet anders, doet het dynck buyghen ende wort egh. Hier siet men dat lmi onder het water kompt ende soeckt opwaers te kommen; of, soot steen is, weeght lichter int water synde dan te vooren. Ende mkn kompt boven water ende wort swaerder. Also wort k omleeghe ende i omhooghe getrocken.   Dits de oorsake dat potten ende houte schotels, hellende, van selfs wederom recht op geraken; in een houte drycantighe pylare dryft het scherpe omleeghe, maer in een steene synckt het scherpe laest, ende het platte gaet vooren, als alles solidum ende vol is. Zwaartepunt Centrum gravitatis navis et putei aquei sunt in eadem linea.   Ten sevenden moet men weten dat het swaerheyts middelpunt van het schip ende het middelpunt des hols int water altyt een selvighe linie syn moeten, die perpendiculaer is opt oppervlack des waters*), tensy den wint etc. het schip doet hellen; maer alles stil synde, salt wederom so kommen.   Ten achtsten so dryft een dynck best als de syde, die het swaerheytsmiddelpunt aldernaest is, onderst is; alwaer dienstich sullen syn de consideratien die ick vooren geschreven hebbe van het vallen ende werpen der swaerheden in de locht. Weet oock dat het solide houdt licht is int water; maer in een schip is houdt noch swaerder dan de locht, dewelcke een groot gat int water maken moet om in te gaen, also dat een schotel of schip, omgekeert, min substantia of houdt onder het water heeft dan rechs staende.   *)  Vgl. Simon Stevin, Byvough der Weeghconst, 201.

[ 259 ]

Den 12en Augusti te Seraeskercke int landt van der Goes.   Dat een schotel dryft, rechs en omgekeert, is omdat beyde voorss. middelpunten op dese twee mannieren in een perpendiculare linie kommen konnen.   Ten 9en is te letten, dat het swaerheytsmiddelpunt somtyts kompt boven het middelpunt des hols, somtyts daeronder, daeruyt verscheyden consideratien ende apparentien vallen. Een houte schotel, omgekeert ende wat hellende, kompt lichter wederom te rechte, dan recht staende alse oock helt, omdat het houdt int water ryst. Ende alsmense (tsy datse rechs of omgekeert staet) wat doet hellen, dan komptse weder op haer vorighe plaetse, alse niet te veel en helt, omdat de opgaende syde meest nederdruckt als meer swaerte buyten het water hebbende. Meyne alles te sien op de twee voorss. middelpunten. Middelpunt Centrum magnitudinis aquae innatantium est supra centrum putei.   Ten 10en, het grootheytsmiddelpunt van hetgene dat int water dryft, is altyt boven het middelpunt des hols int water, want ten kan int water so groot geen hol maken alst selve is, omdatter altyt wat boven water is, twelck mede moet gerekent syn int soecken des middelpunts. Ende men moet acht nemen op de linie, die door de dry centers gaet; dan staet het schip sonder twyffel recht. Schip en andere drijvende dingen Navis et aliorum in aqua natantium.   Ten 11en, so moet men weten te rekenen de topswaerheyt, als, by exempel, wat dat de mast daertoe doet, dewyle sy boven de grootheytsmiddelpunt is. Soeckt het swaerheytsmiddelpunt des masts, so sal de reden des masts syn gelyck de linie tusschen dit middelpunt ende het middelpunt des grootheyts van het schip, het welcke is gelyck den as van een balance, welcken as juyst gaet door het swaerheytsmiddelpunt des balckx.   Ende als het schip helt door den wint, ende deselfde cracht op het seyl eveleens blyvende, dat het schip dan niet om en valt, geschiet door de reden van de seste meditatie voorss., want dan kompter een ander syde des schips int water, die lichter is. Also gaet het anders met eenen hollen stock dan met eenen soliden, want dengenen en hoeft so veel loots niet om recht te staen; om dieswille dat hetgene boven water is, so seer niet neer en dringht gelyck solide houdt. Wederom anders gaet het met eenen stock, die tot aen het water hol is, want het houdt en ryst so sterck int water niet als locht. So gaet het oock anders als het deel int water steen is, want dan staet het van selfs recht omdatter gheen rysinghe en is, ten ware hetgene buyten water is, so groot ende swaer ware, dattet den drangh des onderste overwonne.

[ 260 ]

Sult gedencken dese 11de meditatie te overlegghen in een lichaem, dat met de seste niet te doen en heeft; als in een globe, in dewelcke men onder of boven het center van binnen bedencken mach datmen wilt. Ende hoe de globe draeydt, het hol des waters blyft eenvoudich. Laet een globe van gelyck effen glas int water dryven, ende heght van binnen aen de superficie een stuck houdts, so sult ghy sien dat de globe dryven sal met het houdt onderst, omdat het houdt swaerder is dan de locht die der in is. Doet dan de globe niet half vol waters, so sal de globe so langhe keeren totdat het houdt so verde uyt het water steeckt alst doen soude waert niet geheght, want het soude also wel aen de canten als in den midden konnen dryven. Ende indien binnen in een leghe globe twee swaerheden niet recht overeen geheght en worden, so en sal het swaerste niet recht onderst syn, want alles weeght ter syden meer dan onder of boven. Ende soomen aen des grootheyts middelpunt wat heght met syns swaerheyts middelpunt, so en salt in de globe gheen veranderinghe geven.   In somma alles geschiet gelyck aen een wiel, dat op eenen as draeydt. Maer van buyten is grooter verschil doordien houdt swaer is in de locht ende licht int water. Ende steen, int water kommende, verliest van syn swaerheyt; daerom een houdt van buyten, boven of onder, aengeheght, sal tot aen den opperkant des waters kommen. Aen beyde syden steen geheght, sal het opperste steen het onderste byna uyt het water doen steken. Boven steen ende onder houdt, salt int eerste seer rasch drayen totdat den steen buyten het water is; so dan het houdt noch swaerder is, salt tragher dalen ende aent water kleynder hol int water maken dant swaer weeght, omdat den steen dat wat ophoudt. Houten prisma Prisma ligneum quomodo aquae innatet.   Een plancke overkant int water staende, valt door de reden van de seste meditatie, doch niet gelyck een stock, maer slechs aen weersyden. Twee plancken, aeneen gemaeckt schipswyse*), sodat de eynden syn triangula aequilatera, en konnen met de scherpte niet int water staen, tensyse diep ingaen, want het grootheytsmiddelpunt is leegher dan de twee hoecken, ende daerom wort den hoeck, die begint te vallen, eenen langheren arm; ende die opgaet eenen korteren, ende valt voorst. 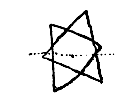Ergo een drycante pylare dryft opt water op syn plat, maer als het grootheyts­middelpunt onder het water is, dan dryft sy op haer kant. Want boven water, in de locht, ist platte swaerder, ende valt nederst; maer int water ist platte lichtst ende ryst eerst op, dewyle dat daerontrent meest lichte deelkens syn, die na boven toe styghen.   Dit verstaet van een lichaem, dat heel eenparich is. Maer een houte drycante pylare binnen hol, te weten vol lochts, daervan moet men oock op de superficies acht nemen, dewelcke grooter is, naer advenant syn binnenste, aen de kanten, dan aen het platte, gelyck dicwils°) bewesen is in figuris isoperimetris et figurarum partibus.   [ *)  In een V-vorm.]       °)  B.v. I, 233, 275.   [ "... dicwils bewesen is ..." bij isoperimetrische figuren (met gelijke omtrek) en delen van figuren. Zie de openbare les, Dordrecht, 1627.]

[ 261 ]

Daerom moet men considereren, dat de superficies sonder dickte is; ende dewyle houte plancken dick syn, soo moetmen die dickte rekenen binnen in te syn (gelyck rechs vooren in de globe geseyt is [<]), waeruyt volcht, dat de kanten noch so veel te swaerder syn. Ende dierhalven de pylare dryft al op haer kant, eer dat se half int water synckt, want het hout is oock also ballast ende onder des grootheyts­middelpunt. Duizeligheid Cerebrum fit vertiginosum propter res versas et specula.   Na dien dat het omdrayen van eenighe dynghen int gesichte, de hersenen oock doet drayen, als savons een brandende kole, een rat dat rasch omloopt, alsmen van hooghe omleeghe siet, — nadien, segghe ic, dat de hersenen de beweginghen van buyten eenichsins volgen, hoe rasser ende grooter de dynghen syn, die roeren, hoemeer dat de hersenen daerdoor ontstelt worden, want een groot rat, een grote kole, een seer hooghe plaetse, doen meer als haer contrarien. Nu dewyle men die macht niet en heeft om groote dynghen rasch te drayen etc., so salmen daertoe den persoon, diemen ontstellen wilt in een spiegel doen kycken, ende den spieghel beweghen gelyckmen wilt, waerdoor alle groote ende kleyne dynghen, die stil ligghen, ende andersins onbeweeghlick syn, sullen schynen te drayen ende doen sulcke effecten in de hersenen alsof se waerlick gedrayt ende beweeght wierden. Dienstich om de mensche te altereren, nadat syn sieckte ende nature verheyscht.

[ Lat. ]   [ v ]

[ 264 ]   12 aug. - [5 nov.] 1623

As op wieltjes Assche des rats op een ander radt rustende.   Tot Weymans*) hebbe ick gesien twee wielkens, waerop men de pinnen van eenen swaren as leght omdat die anders al te styf drucken op hetgene daer sy in draeyen; maer dese wielkens drayen mede om, also dat het drucken allom even styf kompt ende de wielkens rondt blyven. De voorsz pinnen moeten niet perpendiculariter liggen opt opperste van de wielkens, maer een weynich aen de leegher syde, omdat sy door den draey altyt opwaerts styghen. Ick achte, dat de eene superficies der pinnen, die nederwaerts gaet, recht over het centrum van de wielkens moet ligghen. De wielkens behooren van stael te syn, omdat de pinnen daerin gaen moghen. Daer moeten oock yserkens aen het ander vast syn, daer tusschen de pinnen gaende, altyt op één plaetse blyvende, bequamelick door haeren draey de wielkens oock mochten doen draeyen; dienstich, na myn oordeel, om het beletsel van naecksel te minderen.   Weymans seght, dat ment te Luyck in swaere wercken veel gebruyckt.   [>]   *)  Jan Weymans [>] kwam van (bij) Luik, was sinds zeker 1610 in Rotterdam, "sydeverwer", kreeg problemen in de kerk (1625/6), werd verdedigd door Beeckman. Lid van het Collegium Mechanicum [>]. Schouwen Fumariorum ratio.   Als men aen ons nieu schouken een brandende keerse houdt, so wort de vlamme daervan van boven nederwaerts in het schouken getrocken, also dat de vlamme wel uytgaet; twelck een teecken is datter geduerich in het schouken tocht gaet na boven toe.   De reden van desen ende alle andere tochten der schouwen is, dat het in de kamers altyt ordinaris warmer is dan buyten. Nu de warme locht is lichter dan de koude locht, derhalven so gaet de warmte opwaerts, daer se kan, te weten onder een schouwe; ende die opgaende, so kompter nieuwe locht door veynsters, deuren of gerren wederom in de kamer; dewelcke wederom warm wordende door de beslotenheyt van de kamer, ende onder de schouw gerakende, treckt wederom opwaerts ter schouwen uyt, als vooren. Ende dit is de tocht, die alle warmachtighe kamers hebben, tensy datter eenich belet sy, als namentlick dat deuren ende veynsters so dicht toe syn, datter gheen nieuwe locht in kommen en kan door de schouwe, dewelcke den tocht, die de warme locht heeft verhindert met nederwaers te kommen.

[ 265 ]

Het helpt oock den tocht seer als het weder buyten int kouder worden is, want dan wort de locht boven de schouwe ineengedronghen ende treckt mede per fugam vacui.   Het moet oock seer goet syn datter in de schouwen op den heert vier is, ende dattet wel brandt, want het maeckt die locht noch meer op te trecken; ende het vier selve treckt oock op ende maeckt mede tocht, behalven dat het noch veel lochs verdunt. Maer dewyle dat het dadelick vier de locht verteert, dat is te segghen, so dun maeckt, dattet met het vier door alle dynghen treckt, so wort de kamer leger; ende indien der gheen nieuwe locht in en kan kommen deur deuren of veynsters etc., so komtse in door de schouwe ende slaet den roock neder.   De Sonne op de schouwe schynende, maeckt de locht dunne ende onbequaem om den roock te ontfanghen om daerin op te gaen, omdatse byna so dunne is als den roock selver.   [<,>] Perspectief Perspectivæ ratio.   Den 5en November seyde my Hans Willaerts cosyn, de schilder*), datter dry schilders t'Amsterdam syn, die seer gepresen worden ende inde opinie vant verschieten der pylaren [<] oock ter syden; ende daerenboven datse alle dynghen opt ooghpunt, ende daeromtrent, seer net ende sterck schilderen ende de reste als door een schemeringhe gesien synde. Maer de proportionele distantie geobserveert synde, segghe ick dat alles op het bort schyndt gelyck buyten int verschieten.   *)  Hans Willaerts (1589 - 1643) was getrouwd geweest met Beeckmans in 1620 overleden zus Susanne. Hij was "borduerwercker".

[ Lat. ]   [ v ]

[ 271 ]   29 nov. 1623

Regel van drie Regula aurea conversa explicatur.   Philips Fincon, den 29en November my vraghende, waerom datmen in den verkeerden regel van dryen moest het eerste met het tweede multipliceren ende met het derde divideren, hadde ick dese bedenckinghe daerover.   Het is bekent, dat, als een man in thien dagen een stuck werckx maeckt, ende dat men wil weten in hoeveel daghen dat hetselfde stuck werckx van twee mannen soude konnen gemaeckt werden, datmen dan een getal moet soecken, dat so veel kleynder is dan thien daghen als twee mannen meer syn dan één man. Maer dit vindt men in dese proportie: 1 - 5 - 2 - 10, want 5 is so veel kleynder dan 10 als 2 grooter is dan 1, dewyle sy even verde van de uyterste staen, het een onder ende het ander boven.

[ 272 ]

Nu dan so is bekendt, dat de uyterste, samen gemultipliceert, syn so groot als de middelste, samen gemultipliceert, door de reden van de rechten regel van dryen. Maer in den verkeerden is het eerste het eerste ende het laetste het tweede ende het derde het derde, als 1. 10. 2. 5. Dan gemultipliceert met 10 maeckt de rechthoekighe figuere van de twee uyterste gelyck, synde t'gemultipliceerde van 5 ende 2; dat dan door 2 divideerende, moet nootsakelick kommen 5, de ander syde van de rechthoukighe figuere gemaeckt van de middelste 5 ende 2.   Hetselvighe vindt men oock in deselve proportie, so het eerste met het derde ende het tweede met het vierde gestelt wort als 1 - 2 - 5 - 10, want soveel grooter 2 is dan 1, soveel kleynder is 5 dan 10. Ende dan wort het derde gesocht, gelyck te vooren het tweede. Als: Een maeckt het in 10 daghen, in hoeveel daghen maeckent twee mannen?  Facit in 5 daghen, synde het derde getal. Dubbele regel Regula aurea duplex et composita quatuor modis solvitur.   Alsoo heeft oock den dobbelen regel syn fondament in de proportien, die gecomposeert syn, waerdoor de manniere van wercken gepracktiseert is. Maer die de reden daervan weet en kan niet missen.   So 100 £ wint in 12 maenden 8 ƒ, hoeveel sullen winnen 350 £ in 6 maenden? *)   Men moet weten, dat dit door twee simpele regels van dryen kan gemaeckt worden, ende dat op vierderley mannieren. Want dewyle men twee questien heeft, daer men van vraecht, te weten 350 £ ende 6 maenden, so kan het eene eens eerst achter staen, ende eens laest in den regel van dryen, het middelste synde 8 ƒ. Ten anderen, so kan 100 £ eens in de midden staen ende 12 maenden. Aldus:

[ 273 ]

Dit wetende sal groot licht geven om alle regels te resolveren ende daeruyt te sien of se recht of verkeert moeten gewrocht worden. Hieruyt blyckt dat de proportie van 8 ƒ tot 14 ƒ gecomposeert is uyt de proportien van 100 £ tot 350 £ ende 12 m. tot 6 m.; want 100 is tot 350 gelyck 8 tot O, en 12 is tot 6 gelyck O teghen 14. Te weten de eersten teghen de derden gelyck de tweeden teghen de vierden, staen aldus: 100 — 350  gelyck  8  tot O. 12 tot 6  gelyck O  tot 14, ergo 1200 — O — 2100  gelyck  8 — 14   Nu de O uytlatende, welck is 4200, so siet men dat men het eerste met het tweede moet multipliceren om de twee proportien aeneen te hechten ende wort den regel aldus gestelt: 100 £ — 12 m. — 8 ƒ — 350 £ — 6 m. — facit 14 ƒ.   Also doet men oock alser meer proportien gecomposeert worden: Als 10 mannen met 100 pont in 6 maenden, 4 daghen sweeckx besongerende, ende 7 ueren s'daeghs, winnen 8 pont, wat winnen 5 m. met 50 £ in 3 m., 4 d. s. b. ende 3 ueren s'daeghs? Facit O.   [ *)  Voor het teken bij "te winnen", een soort y, is genomen het teken voor gulden (ƒ, het woord staat er niet); 1 pond was 6 gulden. Meer over de regel van drie in:  Marjolein Kool, die conste vanden getale, een studie over Nederlandstalige rekenboeken uit de vijftiende en zestiende eeuw, p. 132.]

[ Lat. ]   [ v ]

[ 277 ]   12 dec. 1623 - [20] jan. 1624

Waarom laarzen vuil worden Caligas suas cur quidam commaculent.   Sommighe lieden becladden int gaen, alst slyckerich weder is, haer kousens ende mantels meer dan andere, omdat sy int laeste van het opheffen van haer voeten een hortjen geven, waerdoor het slyck van haer schoenen afgeschut wort na boven toe, gelyck men het water uyt de salae schut, ofte den reghen van den hoet. Hoe dat die horten ende dat schudden dat doet, hebbe ick vooren ergens geseydt [<], daer ick toonde dat alle dynghen in een beweginghe blyven, daer sy in syn, tot datse belet worden. Also worden oock de schoenen wech geruckt, maer het slyck daerop en isser niet vast aen, blyft derhalven in die beweginghe, daer den voeten in was; welck beweginghe, stercker synde dan het beletsel van vasticheyt, daermede het slyck aen de schoe kleeft, so treckt het daervan ende vlieght syns weeghs, gelyck het met de voet begonnen hadde.

[ Lat. ]   [ v ]

[ 279 ]

Bijziend Myopes cur nictantibus oculis dimidiam duntaxat flammam videant.   Vooren hebbe ick ergens geseydt [<] van der keersen vlamme, waerom datse my, ende al die wat sticksiende syn, grooter schyndt, ja sommighe schyntse wel so groot als eenen grooten Hollandschen kaes. Nu so gebeurt het oock, alsmen ons ooghen half toe doet, dat men dan de vlamme van de keerse oock maer half en siet, daermen nochtans alle andere dynghen geheel blyft siende.   De reden daervan is, dat de stralen, die niet essentieel en syn, door het persen van de ooghen verdwynen, ende het principale corpus der vlamme blyft, sich altyt vertoonende nae de proportie van de distantien. Daerom ist dat door dit half toedoen van de ooghen, de opperste ende onderste onessentiele stralen wel verdwynen, maer de sydtstralen niet, waerdoor de vlamme schyndt lanckworpich te syn, tensy dat men met de vyngher de ooghen tersyden oock perst.   Men sal oock bevinden dat die niet sticksiende en syn, dit verlies van de halve vlamme der keerse niet gewaer en worden, al doen sy haer ooghen half toe, dewyl sy die verschouwelicke stralen niet en hebben; ende sien de vlamme evelleens gelyck ander dynghen, na proportie des afwesens.

[ Lat. ]   [ v ]

[ 280 ]   12 dec. 1623 - [20] jan. 1624

Algebra Cossicarum geniturarum ratio.   De genitueren, daar Clavius van schryft Lib. 6, Prop. 19 Geometriae practicae*) ende Smetius int Duyts in syn Algebra,°) pag. 36, hebben haeren oorspronck uyt den wortel 11, want 11 in sich gemultipliceert is 121, alwaer de genituere is 2, latende de letters, daer de punten onder staen, ledich. Wederom 11 cubicè gemultipliceert is 1331, de genituren 3.3. Wederom icè 13631, de genituren 4.6.4., etc.

De reden dat men in den altyt moet één letter vry laten, in den twee, in den drye, is omdat alsmen 10 met 10 multipliceert, men kryght 100, ende 100 met 100 men kryght 10000, namentlick twee letters meer. Ergo dat tusschen 10 ende 100 is en kan geen vyf letteren bedraghen, dewyle 100 met 100 rechs vyf letteren kryght. Derhalven al de quadraten tusschen 100 ende 10000 en hebben maer twee letteren voor haren radix.   *)  Christoph Clavius, Geometria Practica (Rome 1604), p. 309 (Prop. 19: Radicem cujuslibet generis extrahere).   °)  Anthoni Smyters, Arithmetica, dat is de Reken-konste, 3: Reghel Coss ofte Algebra (Rotterdam 1612).   [Op p. 36: de 'driehoek van Pascal' en het woord 'genituren'; zie ook p. 27-28, 'Van de Cubic-ghetalen, en extractio harer wortelen': "zet 3 als genituren van't cubo". Symbolen: staat voor 'zensus', tweede macht; voor 'zensensus', vierde macht. Franse editie: Rotterdam 1600, zie P. Bockstaele in Gewina, 1979, 45-51.]

[ > ]